图论——最小生成树
图论——最小生成树
A wise man changes his mind, a fool never will
生成树
一个连通图的生成树是一个极小的连通子图,它包含图中全部的n个顶点,但只有构成一棵树的n-1条边。
最小生成树
在这些边中选择N-1条出来,连接所有的N个点。这N-1条边的边权之和是所有方案中最小的。
Prim算法(一般用于稠密图——邻接矩阵)
思想(贪心)
每次将离连通部分的最近的点和点对应的边加入的连通部分,连通部分逐渐扩大,最后将整个图连通起来,并且边长之和最小。
代码
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 505, INF = 0x3f3f3f3f;int g[N][N], dist[N];
int n;
bool st[N];int prim() {memset(dist, 0x3f, sizeof dist);int res = 0;for (int i = 0; i < n; i ++) {int t = -1;for (int j = 1; j <= n; j ++)if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;if (i && dist[t] == INF) return INF;st[t] = true;if (i) res += dist[t];for (int j = 1; j <= n; j ++) dist[j] = min(dist[j], g[t][j]);}return res;
}int main() {int m;cin >> n >> m;memset(g, 0x3f, sizeof g);while (m --) {int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = min(g[a][b], c);}int t = prim();if (t == INF) cout << "impossible" << endl;else cout << t << endl;return 0;
}
Kruskal 算法(一般用于稀疏图——邻接表)
思想
- 将所有边按照权值的大小进行升序排序,然后从小到大一一判断。
- 如果这个边与之前选择的所有边不会组成回路(并查集),就选择这条边;反之,舍去。
- 直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。
- 筛选出来的边和所有的顶点构成此连通网的最小生成树。
代码
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u和点 v 之间存在一条权值为 w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。数据范围
1 < = n < = 1 0 5 1<=n<=10^5 1<=n<=105
1 < = m < = 2 ∗ 1 0 5 1<=m<=2*10^5 1<=m<=2∗105
图中涉及边的边权的绝对值均不超过 1000。
输入样例:
4 5 1 2 1 1 3 2 1 4 3 2 3 2 3 4 4输出样例:
6
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 1e5 + 10, INF = 0x3f3f3f3f;struct node {int a, b, w;bool operator< (node &b)const {return w < b.w;}
}e[N * 2];int p[N];int find(int x) {if (p[x] != x)p[x] = find(p[x]);return p[x];
}int n, m;int kruskal() {sort(e, e + m);for (int i = 1; i <= n; i ++) p[i] = i;int res = 0, cnt = 0;for (int i = 0; i < m; i ++) {int a = e[i].a, b = e[i].b, w = e[i].w;a = find(a), b = find(b);if (a != find(b)){p[a] = p[b];++ cnt;res += w;}}if (cnt < n - 1) return INF;return res;
}int main() {cin >> n >> m;for (int i = 0; i < m; i ++) {int a, b, w;cin >> a >> b >> w;e[i] = {a, b, w};}int t = kruskal();if (t == INF) cout << "impossible" << endl;else cout << t << endl;return 0;
}
相关文章:

图论——最小生成树
图论——最小生成树 A wise man changes his mind, a fool never will 生成树 一个连通图的生成树是一个极小的连通子图,它包含图中全部的n个顶点,但只有构成一棵树的n-1条边。 最小生成树 在这些边中选择N-1条出来,连接所有的N个点。这N-1…...

C++基础 -42- STL库之list链表
———————STL库之list链表——————— 🎄 list链表的格式(需要定义头文件) list<int> data1(4, 100);list<int> data2(4, 500);🎄list链表的合并接口 🎄举例使用合并接口并且验证 data2.merge(data1);list<int>::…...

Backend - Python 序列化
目录 一、作用1:代码块存入数据库 二、作用2:前后端传递数据 (一)前端 1. JSON.stringify() 2. JSON.parse() (二)后端 1. json.dumps() (1)作用 (2)…...

初级数据结构(一)——顺序表
文中代码源文件已上传:数据结构源码 <-上一篇 NULL | 初级数据结构(二)——链表 下一篇-> 1、顺序表的特点 1.1、数组 现实中数据记录一般都记录在表格中,如进货单、菜单等,它们的最大特点就是…...
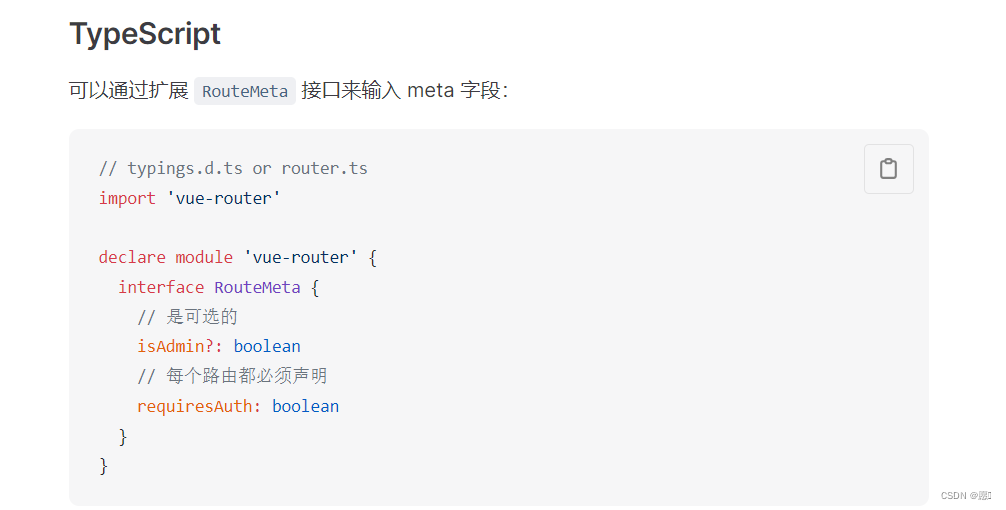
实现:切换页面切换标题,扩展 vue-router 的类型
布局容器-页面标题 网址:https://router.vuejs.org/zh/guide/advanced/meta 给每一个路由添加 元信息 数据 router/index.ts const router createRouter({history: createWebHistory(import.meta.env.BASE_URL),routes: [{ path: /login, component: () > im…...

已通过考试和认证注册以及后续计划表
已通过考试和认证注册以及后续计划表 软考 - 计算机技术与软件专业技术资格(水平)考试信息系统集成及服务项目管理人员工程类考试计划你关注的证书样子 软考 - 计算机技术与软件专业技术资格(水平)考试 高级 信息系统项目管理师&…...

开源计算机视觉库OpenCV详解
目录 1、概述 2、OpenCV详细介绍 2.1、OpenCV的起源 2.2、OpenCV开发语言 2.3、OpenCV的应用领域 3、OpenCV模块划分 4、OpenCV源码文件结构 4.1、根目录介绍 4.2、常用模块介绍 4.3、CUDA加速模块 5、OpenCV配置以及Visual Studio使用OpenCV 6、关于Lena图片 7、…...
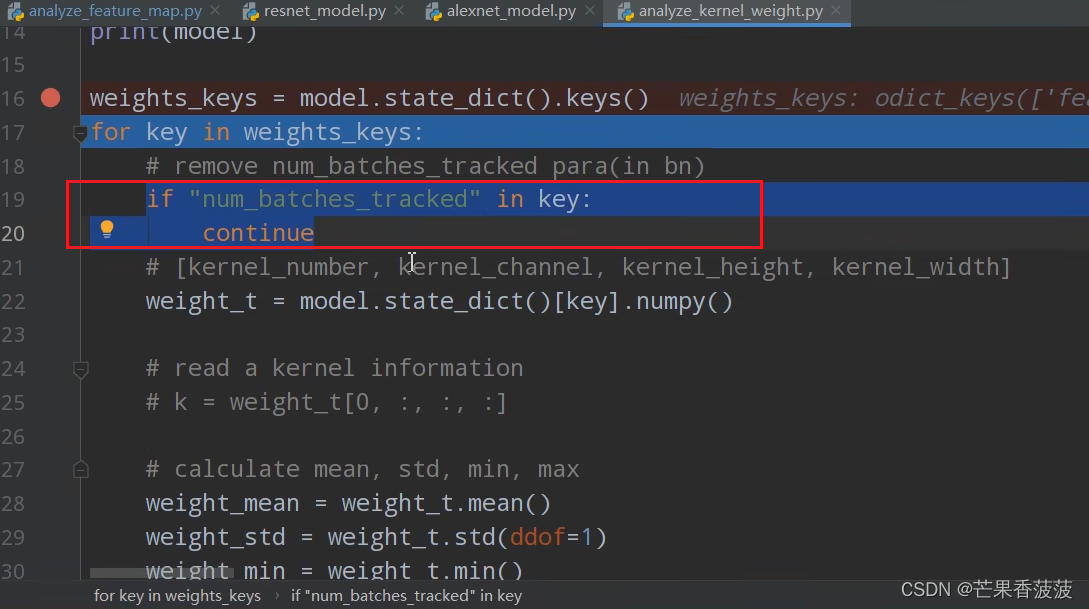
使用pytorch查看中间层特征矩阵以及卷积核参数
这篇是我对哔哩哔哩up主 霹雳吧啦Wz 的视频的文字版学习笔记 感谢他对知识的分享 1和4是之前讲过的alexnet和resnet模型 2是分析中间层特征矩阵的脚本 3是查看卷积核参数的脚本 1设置预处理方法 和图像训练的时候用的预处理方法保持一致 2实例化模型 3载入之前的模型参数 4载入…...

HarmonyOS4.0从零开始的开发教程09页签切换
HarmonyOS(七)页签切换 List组件和Grid组件的使用 Tabs组件的使用 概述 在我们常用的应用中,经常会有视图内容切换的场景,来展示更加丰富的内容。比如下面这个页面,点击底部的页签的选项,可以实现“首页…...
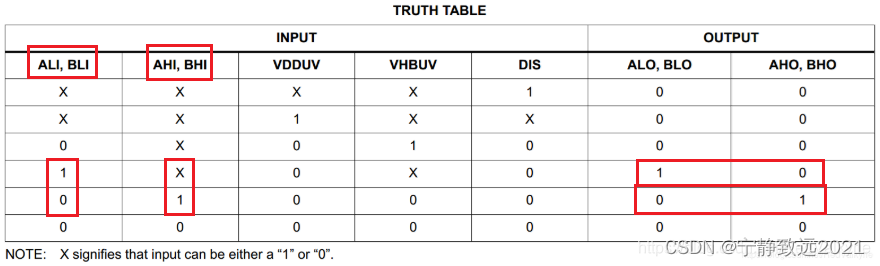
大电流H桥电机驱动电路的设计与解析(包括自举电路的讲解,以IR2104+LR7843为例)
大电流H桥电机驱动电路的设计与解析(包括自举电路的讲解,以IR2104LR7843为例) 电机驱动板主要采用两种驱动芯片,一种是全桥驱动(如:HIP4082),一种是半桥驱动(如ÿ…...
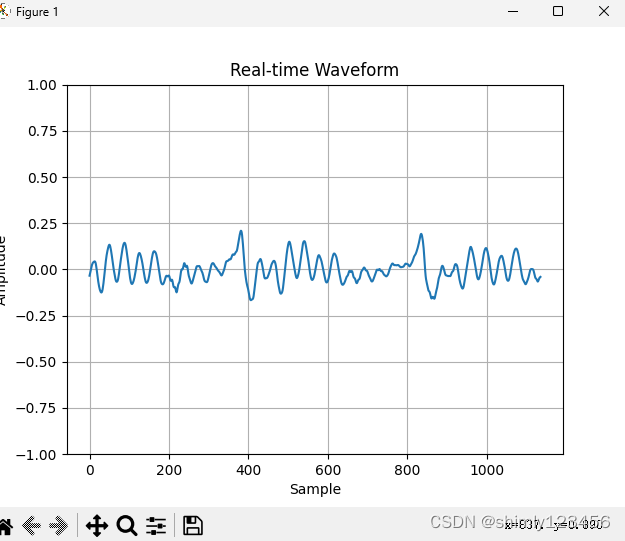
windows11 windows 11 (win11 win 11) 怎么安装 Python3 ? numpy? sounddevice? 声音信号处理库?
首先确认要安装的 sounddevice 库,链接:https://python-sounddevice.readthedocs.io/en/0.4.6/ 根据文档,可知最新的 sounddevice 版本是 0.4.6 进入安装页面查看,发现 Newest sounddevice 可以使用 pip 安装,如下图…...

git如何配置多个远程仓库,并且进行切换
一、配置多个远程仓库并进行切换,请按照以下步骤进行操作: 打开命令行终端,并进入您的 Git 仓库所在的目录。添加第一个远程仓库,使用以下命令:git remote add origin <第一个远程仓库的 URL>这里将远程仓库命名…...

计算机存储单位 + 程序编译过程
C语言的编译过程 计算机存储单位 头文件包含的两种方式 使用 C/C 程序常用的IDE 常用的C语言编译器: 在选择编译器时,需考虑平台兼容性、性能优化、调试工具和开发人员的个人偏好等因素。 详细教程可转 爱编程的大丙...

vue路由导航守卫(全局守卫、路由独享守卫、组件内守卫)
目录 一、什么是Vue路由导航守卫? 二、全局守卫 1、beforeEach 下面是一个beforeEach的示例代码: 2、beforeResolve 下面是一个beforeResolve的示例代码: 3、afterEach 下面是一个afterEach的示例代码: 三、路由独享守卫…...
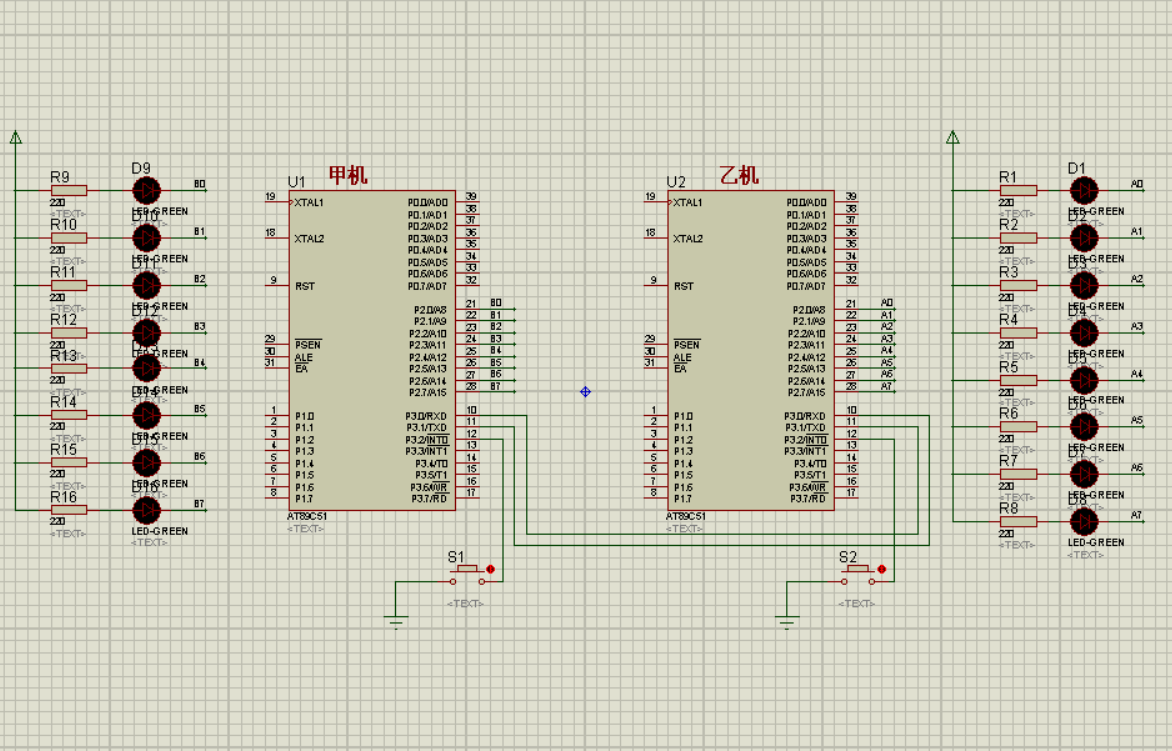
单片机双机通信控制跑马灯
实验要求 两个单片机各驱动8个LED灯,构成两个跑马灯,要求甲单片机LED的点亮方式是从上至下,首先是最上面第一个点亮、其次是前两个点亮、其次是前三个点亮……直至8个灯全部点亮,8个灯全部灭,重复这个过程,…...

微信小程序:button微信开放能力打开客服会话分享到聊天框
文档 https://developers.weixin.qq.com/miniprogram/dev/component/button.html 打开客服会话 按钮关键属性 open-type"contact"功能按钮 <button class"mo-open-type"open-type"contact"> </button>分享 <button class&q…...
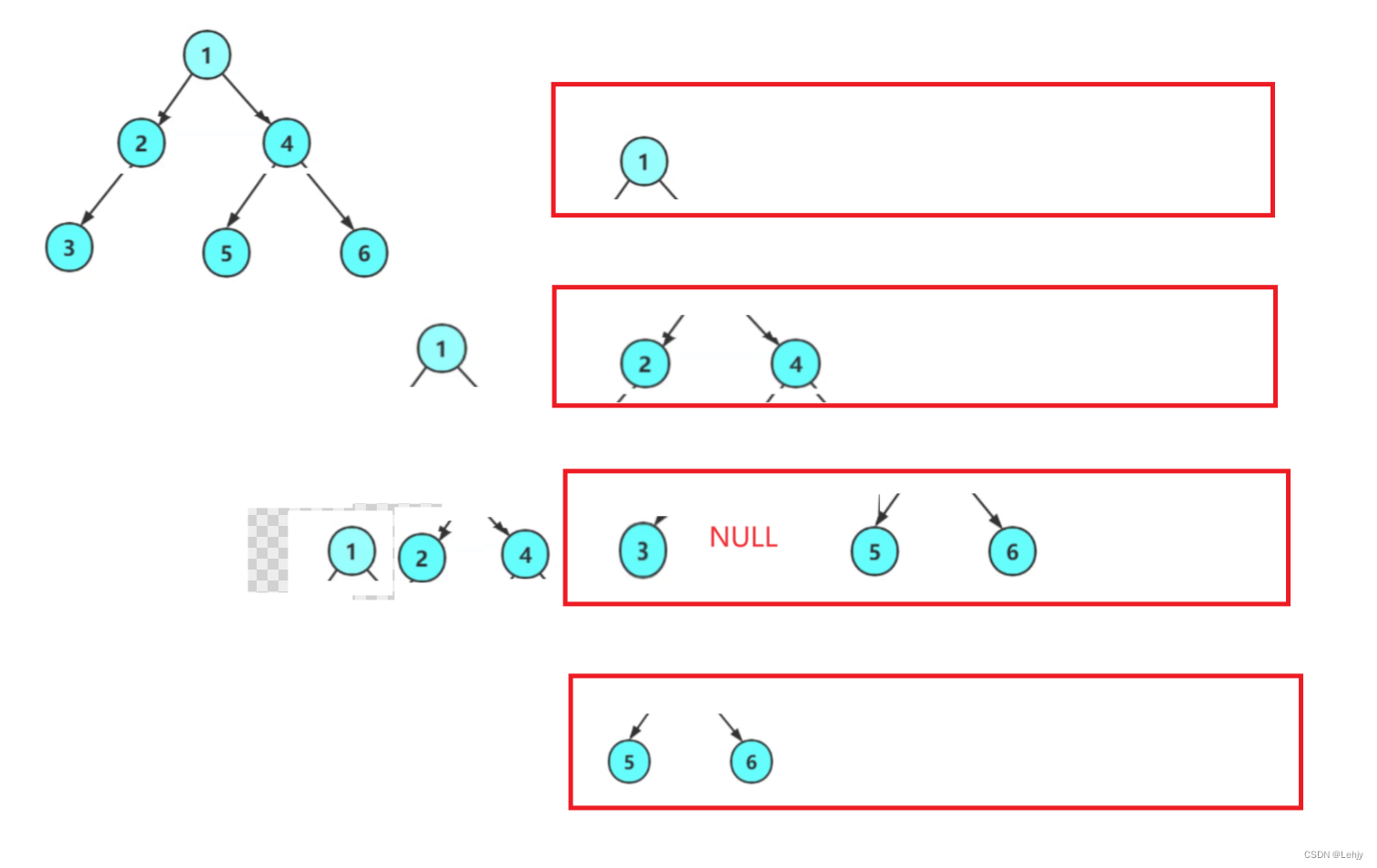
【数据结构】——队列实现二叉树的功能
前言:二叉树的实现方式多种多样,有数组实现满二叉树,有链表实现完全二叉树,今天我们就用队列来实现二叉树。 创建二叉树: typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data;struct BinaryTre…...
【已解决】Win7虚拟机安装VMtools报错
在做以前的实验的时候发现要用到Win7虚拟机,于是就安装了一个Win7的虚拟机,但是发现屏幕太小,而且来回复制文本、复制文件太不方便了,索性就安装了VMtools,发现还安装不成– 情况1 报错:本程序需要您将此…...
)
华为OD机试真题-小明找位置-2023年OD统一考试(C卷)
题目描述: 小朋友出操,按学号从小到大排成一列;小明来迟了,请你给小明出个主意,让他尽快找到他应该排的位置。 算法复杂度要求不高于nLog(n);学号为整数类型,队列规模<10000; 输…...

2023.2版idea安装教程,现在jdk8已经过去式了,不同idea支持的jdk不同。升级jdk后idea也要随之升级
下载idea2023.2版本,下载之前需要删除之前的版本,一定要删除干净,删除程序要勾选那两个delete 下载路径:其他版本 - IntelliJ IDEA (jetbrains.com.cn) 选择2023.2版本 下载后进入安装程序,选择安装目录,然…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
