C#最小二乘法线性回归
文章目录
- SimpleRegression
- MultipleRegression
MathNet系列:矩阵生成 \quad 矩阵计算
LinearRegression是MathNet的线性回归模块,主要包括SimpleRegression和MultipleRegression这两个静态类,前者提供了最小二乘法的线性拟合,后者则主要提供一些矩阵方法。后文中,二者简称为SR和MR。
SimpleRegression
SR中提供了静态方法Fit,对给定的两组数 x , y x,y x,y,找到一组参数 a , b a,b a,b,使之满足 y = a + b x y=a+bx y=a+bx,相应地其返回值是一个元组 ( a , b ) (a,b) (a,b),示例如下
Random r = new Random(42);
double[] xs = Enumerable.Range(0, 100).Select(x=>x*1.0).ToArray();
var ys = xs.Select(x => 10 * x + 5 + r.NextSingle()).ToArray();var ab = SimpleRegression.Fit(xs, ys);
Console.WriteLine(ab);
//(5.378808571430682, 10.00077465365039)
其中,预设函数为 y = 10 x + 5 y=10x+5 y=10x+5,但由于加上一个恒为正数的随机浮点数,所以 a a a的值最终变大了一些,而 b b b的值几乎就等于10了。
MultipleRegression
MR顾名思义,用于解决多线性回归问题,其多项式形式如下
x 00 β 0 + x 01 β 1 + ⋯ + x 0 n β n = y 0 x 10 β 0 + x 11 β 1 + ⋯ + x 1 n β n = y 1 ⋯ x m 0 β 0 + x m 1 β 1 + ⋯ + x m n β n = y n \begin{aligned} x_{00}\beta_0+x_{01}\beta_1+&\cdots+x_{0n}\beta_n=y_0\\ x_{10}\beta_0+x_{11}\beta_1+&\cdots+x_{1n}\beta_n=y_1\\ &\cdots\\ x_{m0}\beta_0+x_{m1}\beta_1+&\cdots+x_{mn}\beta_n=y_n\\ \end{aligned} x00β0+x01β1+x10β0+x11β1+xm0β0+xm1β1+⋯+x0nβn=y0⋯+x1nβn=y1⋯⋯+xmnβn=yn
这种问题一般可以简化为矩阵形式 X β = Y X\beta=Y Xβ=Y,从而MR中提供的一系列函数,目的都是得到 X β = Y X\beta=Y Xβ=Y中的 β \beta β,共有四个函数,采用了不同的方法,分别为
- DirectMethod 使得残差最小。
- NormalEquations 使用了cholesky分解。
- QR 使用QR分解
- Svd 使用奇异值分解
以DirectMethod示例如下
var MB = Matrix<double>.Build;
var VB = Vector<double>.Build;
Random r = new Random(42);var m = MB.Random(100, 2);
var ys = Enumerable.Range(0, 100).Select(i => 20 * m[i, 0] + 40 * m[i, 1] + 2 + r.NextSingle()).ToArray();
var v = VB.DenseOfArray(ys);var abc = MultipleRegression.DirectMethod(m, v);
Console.WriteLine(abc);
//19.7598
//40.4447
相关文章:

C#最小二乘法线性回归
文章目录 SimpleRegressionMultipleRegression MathNet系列:矩阵生成 \quad 矩阵计算 LinearRegression是MathNet的线性回归模块,主要包括SimpleRegression和MultipleRegression这两个静态类,前者提供了最小二乘法的线性拟合,后…...

ULAM公链第九十六期工作总结
迈入12月,接下来就是雪花,圣诞,新年和更好的我们!愿生活不拥挤,笑容不必刻意,愿一切美好如期而至! 2023年11月01日—2023年12月01日关于ULAM这期工作汇报,我们通过技术板块ÿ…...

基于Echarts的大数据可视化模板:智慧交通管理
目录 引言智慧交通管理的重要性ECharts在智慧交通中的作用智慧交通管理系统架构系统总体架构数据收集与处理Echarts与大数据可视化Echarts库以及其在大数据可视化领域的应用优势开发过程和所选设计方案模板如何满足管理的特定需求模板功能与特性深入解析模板提供的各项功能模板…...

C#-快速剖析文件和流,并使用
目录 一、概述 二、文件系统 1、检查驱动器信息 2、Path 3、文件和文件夹 三、流 1、FileStream 2、StreamWriter与StreamReader 3、BinaryWriter与BinaryReader 一、概述 文件,具有永久存储及特定顺序的字节组成的一个有序、具有名称的集合; …...

【Linux】如何在Ubuntu 20.04上安装PostgreSQL
介绍 PostgreSQL或Postgres是一个关系数据库管理系统,提供SQL查询语言的实现。它符合标准,具有许多高级功能,如可靠的事务和无读锁的并发性。 本指南演示了如何在Ubuntu 20.04服务器上快速启动和运行Postgres,从安装PostgreSQL到…...

IT程序员面试题目汇总及答案-计算机面试
程序员面试题目汇总及答案-计算机面试 问题1:请你描述一下你在过去的工作中遇到的一个技术难题,你是如何解决的? 答案1:在我之前的工作中,我遇到了一个涉及大数据处理的问题。由于数据量巨大,传统的处理方法无法在规定的时间内完成。我最后采用了一种分布式计算的方法,…...

【Flink on k8s】- 5 - 简要介绍 Flink
目录 1、了解流计算框架 1.1 分代 1.2 流计算框架对比 2、Flink 的应用场景 2.1 Data anal...

物联网安全芯片ACL16 采用 32 位内核,片内集成多种安全密码模块 且低成本、低功耗
ACL16 芯片是研制的一款32 位的安全芯片,专门面向低成本、低功耗的应用领域, 特别针对各类 USB KEY 和安全 SE 等市场提供完善而有竞争力的解决方案。芯片采用 32 位内核,片内集成多种安全密码模块,包括SM1、 SM2、SM3、 SM4 算法…...

【Linux top命令】
文章目录 深入了解Linux top命令:实时监控系统性能1. 什么是top命令?2. 使用top命令3. top命令交互操作 深入了解Linux top命令:实时监控系统性能 1. 什么是top命令? top命令是一个用于实时监控系统性能的文本界面工具。它显示当…...

深入理解 Promise:前端异步编程的核心概念
深入理解 Promise:前端异步编程的核心概念 本文将帮助您深入理解 Promise,这是前端异步编程的核心概念。通过详细介绍 Promise 的工作原理、常见用法和实际示例,您将学会如何优雅地处理异步操作,并解决回调地狱问题。 异步编程和…...
Linux 和 macOS 的主要区别在哪几个方面呢?
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...
)
springboot(ssm寝室小卖部系统 宿舍小商店网站Java(codeLW)
springboot(ssm寝室小卖部系统 宿舍小商店网站Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0&#x…...
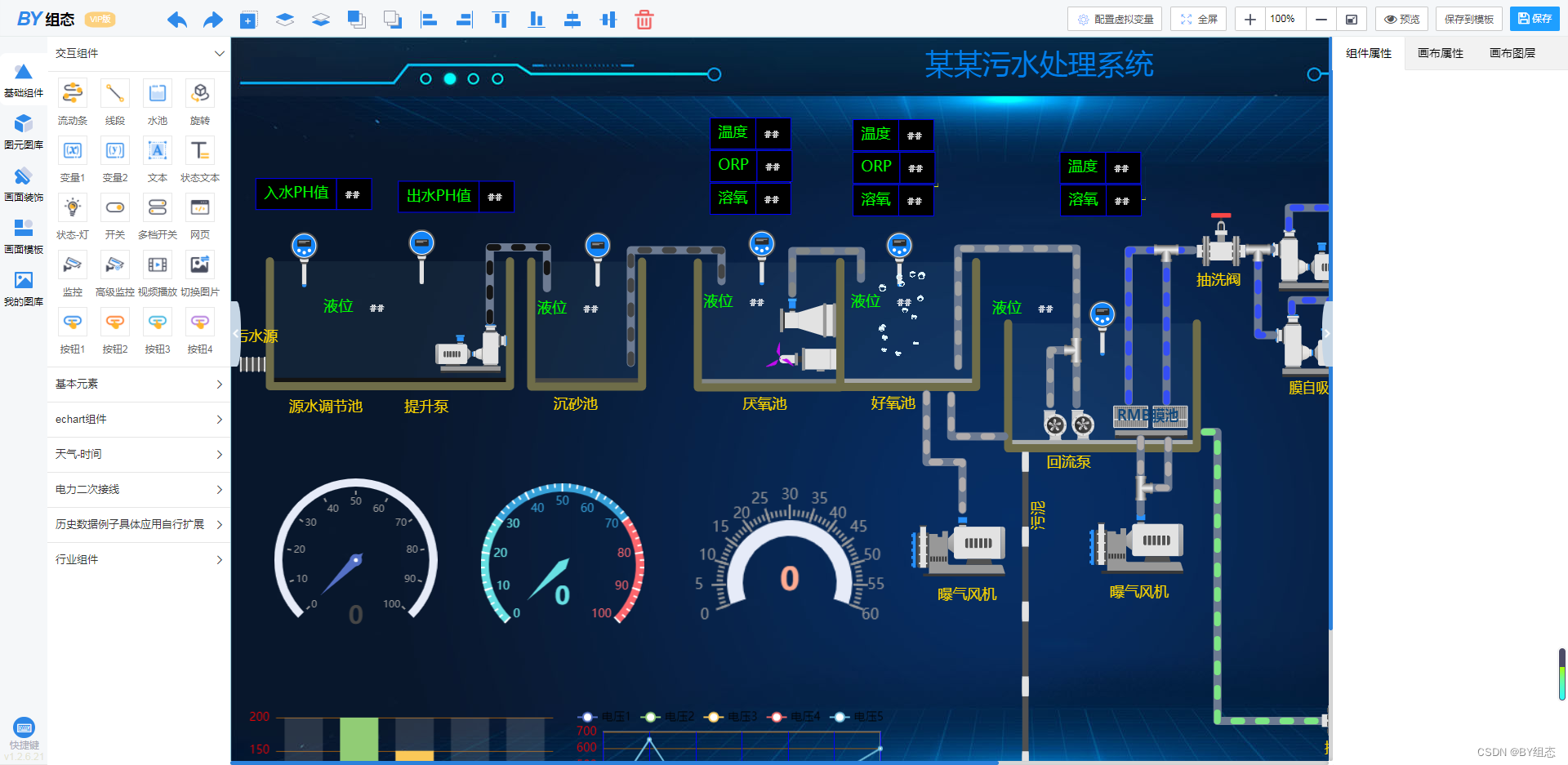
什么是web组态?一文读懂web组态
随着工业4.0的到来,物联网、大数据、人工智能等技术的融合应用,使得工业领域正在经历一场深刻的变革。在这个过程中,web组态技术以其独特的优势,正在逐渐受到越来越多企业的关注和认可。那么,什么是web组态?…...
)
华为OD机试真题-智能成绩表-2023年OD统一考试(C卷)
题目描述: 小明来到某学校当老师,需要将学生按考试总分或单科分数进行排名,你能帮帮他吗? 输入描述: 第1行输入两个整数,学生人数n和科目数量m。0<n<100,0<m<10 第2行输入m个科目名称,彼此之间用空格隔开。科目名称只由英文字母构成,单个长度不超过10个字符…...

YOLOv5独家原创改进:SPPF自研创新 | 可变形大核注意力(D-LKA Attention),大卷积核提升不同特征感受野的注意力机制
💡💡💡本文自研创新改进: 可变形大核注意力(D-LKA Attention)高效结合SPPF进行二次创新,大卷积核提升不同特征感受野的注意力机制。 收录 YOLOv5原创自研 https://blog.csdn.net/m0_63774211/category_12511931.html 💡💡💡全网独家首发创新(原创),适合p…...

算法:进制之前的转换
1. X进制转换成十进制-V1: /*** 笨办法,从左往右开始* Tips:只支持正数** param num* param radix* return*/private static Integer xToTenV1(String num, Integer radix) {if (num.length() 0 || num.charAt(0) -) {throw new IllegalArg…...
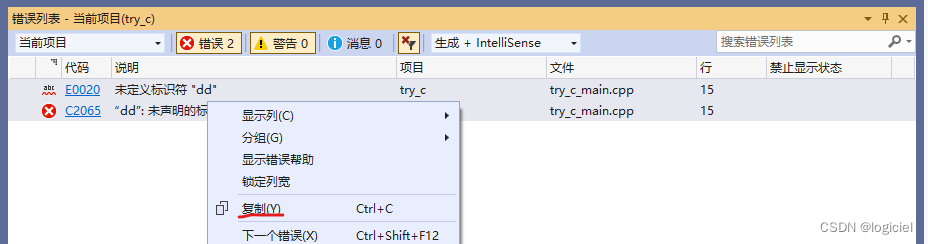
VS2009和VS2022的错误列表可复制粘贴为表格
在VS2019或VS2022中,可看到如下错误列表: 如果复制这两行错误信息: 然后把它粘贴到word文件,就可以看到以下表格: 严重性 代码 说明 项目 文件 行 禁止显示状态 错误(活动) E0020 未定义标识符 "dd"…...
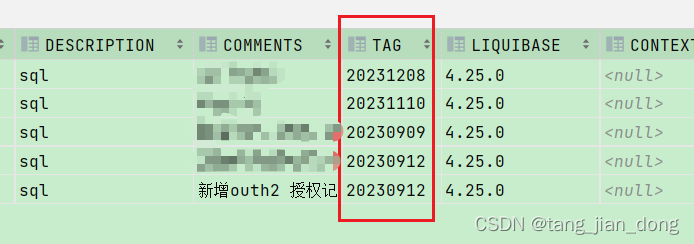
springboot3 liquibase SQL执行失败自动回滚,及自动打tag
一: 自动执行回滚, 已执行成功的忽略,新sql执行失败则执行新sql文件中的回滚sql pom.xml <dependency> <groupId>org.liquibase</groupId> <artifactId>liquibase-core</artifactId> <version>4.25.0&…...
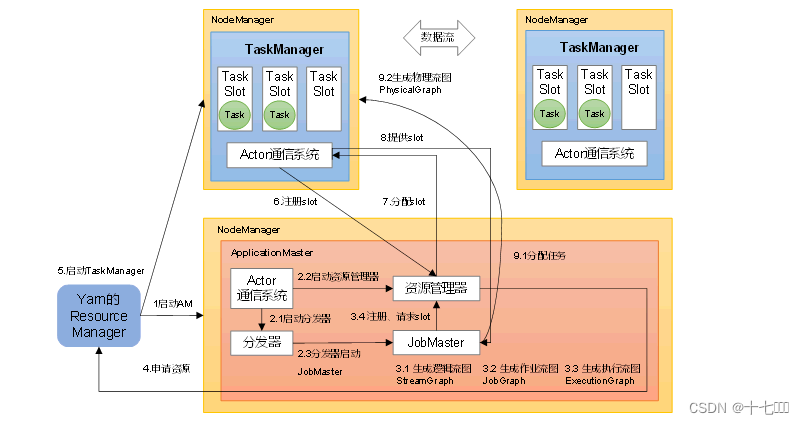
Flink入门之核心概念(三)
任务槽 TaskSlots: 任务槽,是TaskManager提供的用于执行Task的资源(CPU 内存) TaskManager提供的TaskSlots的个数:主要由Taskmanager所在机器的CPU核心数来决定,不能超过CPU的最大核心数 1.可以在flink/conf/flink-c…...
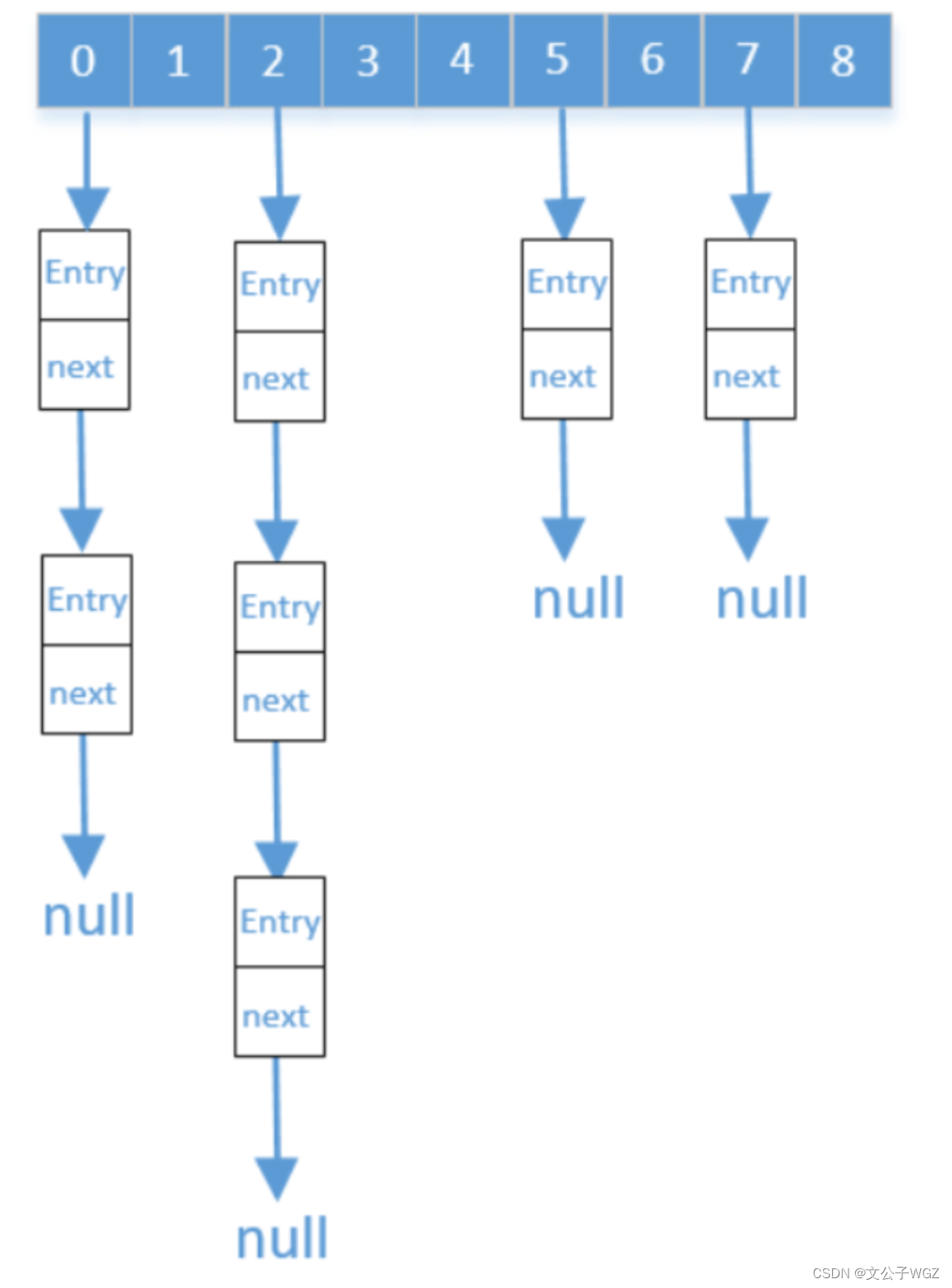
算法备胎hash和队列的特征——第五关青铜挑战
内容1.Hash存储方式2.Hash处理冲突的方式3.队列存储的基本特征4.如何使用链表来实现栈 1.Hash 基础 1.1Hash的概念和基本特征 哈希(Hash)也称为散列,就是把任意长度的输入,通过散列算法,变换成固定长度的输出&#…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
