C++新经典模板与泛型编程:策略类模板
策略类模板
在前面的博文中,策略类SumPolicy和MinPolicy都是普通的类,其中包含的是一个静态成员函数模板algorithm(),该函数模板包含两个类型模板参数。其实,也可以把SumPolicy和MinPolicy类写成类模板—直接把algorithm()中的两个类型模板参数搬到类定义上面作为类模板的模板参数就可以了。类模板SumPolicy和MinPolicy的实现代码如下。
template<typename sumT,typename T>
struct SumPolicy
{static void algorithm(sumT& sum, const T& value){sum += value;}
};template<typename minT,typename T>
struct MinPolicy
{static void algorithm(minT& min, const T& value){if (min > value)min = value;}
};
当然,同样要修改funcsum()函数模板,该函数模板的第3个类型模板参数要作出改变,当前第3个类型模板参数的默认值是SumPolicy,这是一个类型,但是,修改后的SumPolicy已经是一个类模板了,所以funcsum()函数模板的第3个模板参数必须是一个模板模板参数。修改后的funcsum()函数模板如下。
// 这里的class也可以写成typename
template<typename T,typename U = SumFixedTraits<T>,template<class,class> class V = SumPolicy>
auto funcsum(const T* begin, const T* end)
{typename U::sumT sum = U::initValue();for (;;){V<U::sumT, T>::algorithm(sum, *begin);// T时数组成员类型,U是固定萃取类模板,从中可以提取出计算的结果类型(U::sumT)// 以及结果的初值,V是策略类模板,用于实现具体算法(求和,求最小值等)if (begin == end)break;++begin;}return sum;
}
完整且完美的代码,如下:
#include "killCmake.h"#include<string>using namespace std;template<typename T>
struct SumFixedTraits;template<>
struct SumFixedTraits<char>
{using sumT = int;static sumT initValue() {return 0;}
};template<>
struct SumFixedTraits<double>
{using sumT = double;static sumT initValue() {return 0.0;}
};template<typename T>
struct MinFixedTraits;template<>
struct MinFixedTraits<int>
{// 求最小值,结果类型与元素类型相同即可// 为名字统一,都用sumT这个名字using sumT = int;static sumT initValue(){// 这里给整型最大值,相信任何一个数组元素都不会比这个值更大// 因此可以顺利找到数组元素中的最小值return INT_MAX;}
};template<typename sumT,typename T>
struct SumPolicy
{static void algorithm(sumT& sum, const T& value){sum += value;}
};template<typename minT,typename T>
struct MinPolicy
{static void algorithm(minT& min, const T& value){if (min > value)min = value;}
};// 这里的class也可以写成typename
template<typename T,typename U = SumFixedTraits<T>,template<class,class> class V = SumPolicy>
auto funcsum(const T* begin, const T* end)
{typename U::sumT sum = U::initValue();for (;;){V<typename U::sumT, T>::algorithm(sum, *begin);// T时数组成员类型,U是固定萃取类模板,从中可以提取出计算的结果类型(U::sumT)// 以及结果的初值,V是策略类模板,用于实现具体算法(求和,求最小值等)if (begin == end)break;++begin;}return sum;
}int main()
{int my_int_array1[] = { 10,15,20 };std::cout << funcsum<int, MinFixedTraits<int>, MinPolicy>(& my_int_array1[0], & my_int_array1[2]) << std::endl;return 0;
}
萃取技术与策略技术的比较
- 之前的博文,学习了
萃取(trait)技术,也学习了策略(policy)技术,对于萃取技术,通过范例展示了固定萃取和值萃取;对于策略技术,展示了算法策略。萃取技术和策略技术很相似,注意它们之间的相同与不同之处。
- (1)两种技术都像一个中间件一样,夹在不同的功能代码之间,使代码之间的调用(交互)更加灵活。
- (2)萃取技术传入一个类型,萃取出另外一个类型或值(注重类型或值);而策略技术是传入一个类型,萃取出一个算法,或者说是一个不同的功能实现(注重动作或行为)。因此,书写策略类(类模板)时通常都需要包含成员函数以实现指定的行为。但在实际的项目实现中,也可能会在萃取类中实现某些动作或行为,从这个角度来讲,两种技术有时区分并不是那么明显。
- (3)萃取技术一般通过一个类模板来实现,通常包含类模板的泛化版本和多个特化版本。而策略技术用普通类或类模板都可以实现。
相关文章:

C++新经典模板与泛型编程:策略类模板
策略类模板 在前面的博文中,策略类SumPolicy和MinPolicy都是普通的类,其中包含的是一个静态成员函数模板algorithm(),该函数模板包含两个类型模板参数。其实,也可以把SumPolicy和MinPolicy类写成类模板—直接把algorithm()中的两…...
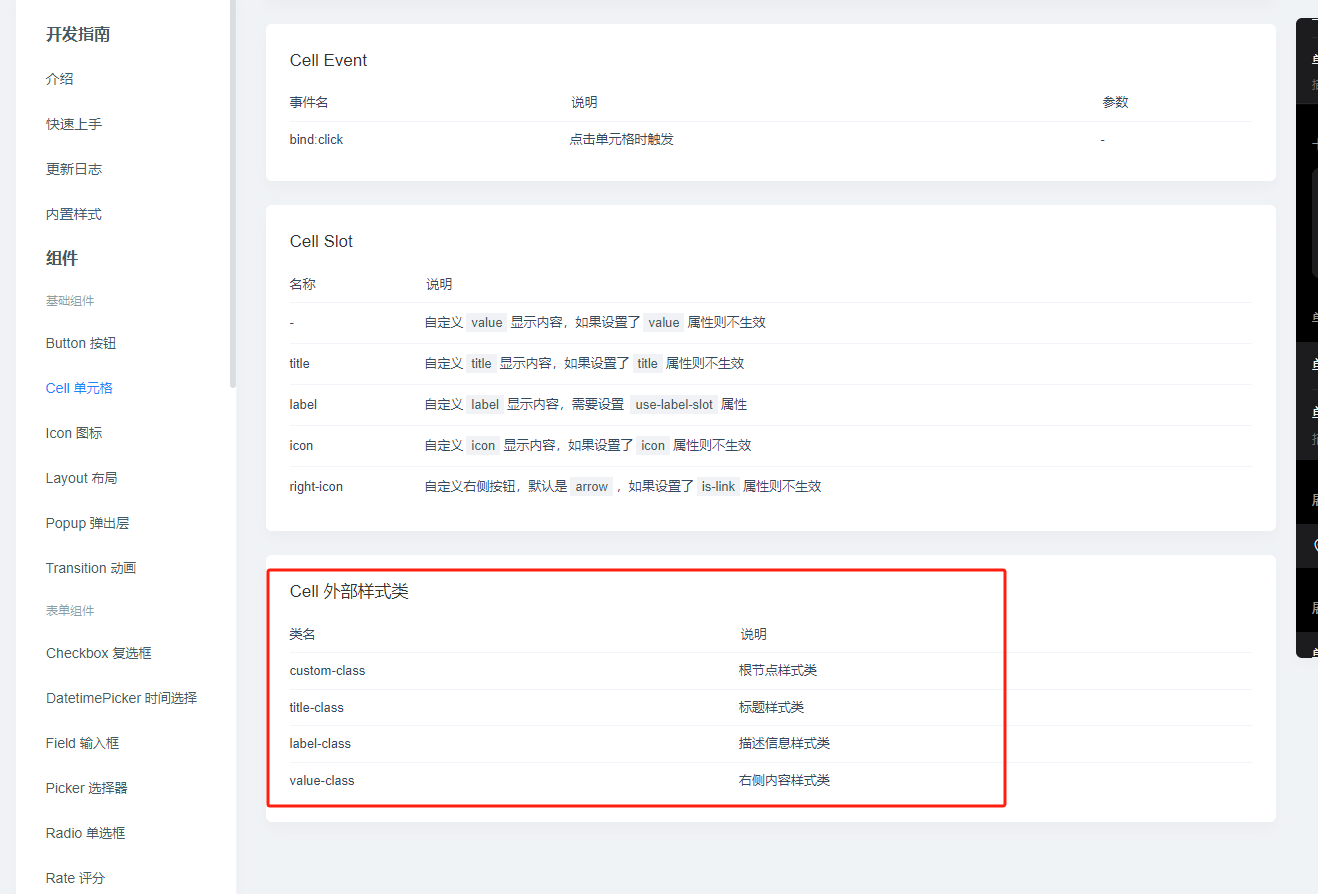
微信小程序引入Vant Weapp修改样式不起作用,使用外部样式类进行覆盖
一、引入Vant Weapp后样式问题 在项目中使用第三方组件修改css样式时,总是出现各种各样问题,修改的css样式不起作用,没有效果,效果不符合预期等。 栗子(引入一个搜索框组件)实现效果: 左侧有一个搜索文字背景为蓝色,接着跟一个搜索框 wxml <view class"container&q…...

python核酸检测 青少年电子学会等级考试 中小学生python编程等级考试二级真题答案解析2022年6月
目录 python核酸检测 一、题目要求 1、编程实现 2、输入输出...

搭建React项目,基于Vite+React+TS+ESLint+Prettier+Husky+Commitlint
基于ViteReactTSESLintPrettierHuskyCommitlint搭建React项目 node: 20.10.0 一、创建项目 安装包管理器pnpm npm i pnpm -g基于Vite创建项目 pnpm create vitelatest web-gis-react --template react-ts进入项目目录安装依赖 $ cd web-gis-react $ pnpm i启动项目 $ pnpm…...

ChatGPT在国内的使用限制,国内的ChatGPT替代工具
人工智能技术的发展不仅改变了我们的生活方式,也在各行各业发挥着越来越重要的作用。ChatGPT(Generative Pre-trained Transformer)作为一种先进的自然语言处理模型,由OpenAI推出,其在生成人类般流畅对话方面表现出色。…...

服务器如何保证数据安全_Maizyun
服务器如何保证数据安全 在当今的数字化时代,数据安全已经成为企业和社会组织必须面对的重要问题。服务器作为存储和处理大量数据的核心组件,必须采取有效的措施来确保数据的安全。本文将探讨服务器如何保证数据安全。 一、访问控制和身份认证 访问控…...

sql2005日志文件过大如何清理
由于安装的时候没有计划好空间,默认装在系统盘,而且又没有做自动备份、截断事务日志等,很快LDF文件就达到十几G,或者几十G ,此时就不得不处理了。 备份和计划就不说了,现在就说下怎么把它先删除吧…...
Linux--学习记录(2)
解压命令: gzip命令: 参数: -k:待压缩的文件会保留下来,生成一个新的压缩文件-d:解压压缩文件语法: gzip -k pathname(待压缩的文件夹名)gzip -kd name.gz(待解压的压缩包名&#x…...

字符串函数`strlen`、`strcpy`、`strcmp`、`strstr`、`strcat`的使用以及模拟实现
文章目录 🚀前言🚀库函数strlen✈️strlen的模拟实现 🚀库函数strcpy✈️strcpy的模拟实现 🚀strcmp✈️strcmp的模拟实现 🚀strstr✈️strstr的模拟实现 🚀strcat✈️strcat的模拟实现 🚀前言 …...
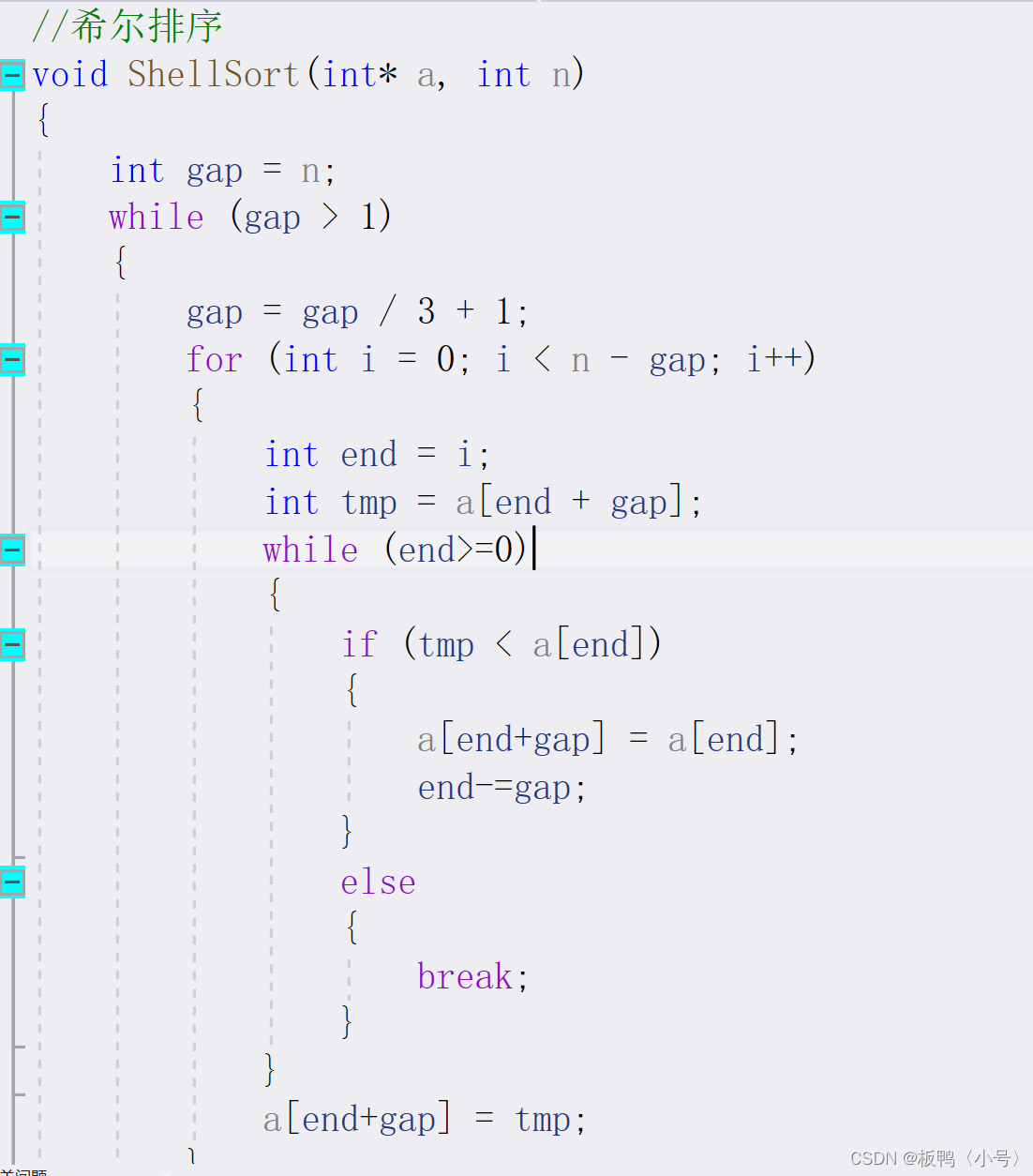
插入排序与希尔排序(C语言实现)
1.插入排序 由上面的动图可以知道插入排序的逻辑就是从第一个元素开始往后遍历,如果找到比前一个元素小的(或者大的)就往前排,所以插入排序的每一次遍历都会保证前面的数据是有序的,接下类用代码进行讲解。 我们这里传…...
)
【微软技术栈】与其他.NET语言的互操作性 (C++/CLI)
本文内容 使用 C# 索引器实现 C# 的 is 和 as 关键字实现 C# 的 lock 关键字 本节中的主题介绍如何在 Visual C 中创建程序集,这些程序集使用或提供以 C# 或 Visual Basic 编写的程序集的功能。 1、使用 C# 索引器 Visual C 不包含索引器;它具有索引…...

TCPUDP使用场景讨论
将链路从TCP改为UDP会对通信链路产生以下影响和注意事项: 可靠性:UDP是无连接的协议,与TCP相比,它不提供可靠性保证和重传机制。因此,当将链路从TCP改为UDP时,通信的可靠性会降低。如果在通信过程中丢失了U…...

C#最小二乘法线性回归
文章目录 SimpleRegressionMultipleRegression MathNet系列:矩阵生成 \quad 矩阵计算 LinearRegression是MathNet的线性回归模块,主要包括SimpleRegression和MultipleRegression这两个静态类,前者提供了最小二乘法的线性拟合,后…...

ULAM公链第九十六期工作总结
迈入12月,接下来就是雪花,圣诞,新年和更好的我们!愿生活不拥挤,笑容不必刻意,愿一切美好如期而至! 2023年11月01日—2023年12月01日关于ULAM这期工作汇报,我们通过技术板块ÿ…...

基于Echarts的大数据可视化模板:智慧交通管理
目录 引言智慧交通管理的重要性ECharts在智慧交通中的作用智慧交通管理系统架构系统总体架构数据收集与处理Echarts与大数据可视化Echarts库以及其在大数据可视化领域的应用优势开发过程和所选设计方案模板如何满足管理的特定需求模板功能与特性深入解析模板提供的各项功能模板…...

C#-快速剖析文件和流,并使用
目录 一、概述 二、文件系统 1、检查驱动器信息 2、Path 3、文件和文件夹 三、流 1、FileStream 2、StreamWriter与StreamReader 3、BinaryWriter与BinaryReader 一、概述 文件,具有永久存储及特定顺序的字节组成的一个有序、具有名称的集合; …...

【Linux】如何在Ubuntu 20.04上安装PostgreSQL
介绍 PostgreSQL或Postgres是一个关系数据库管理系统,提供SQL查询语言的实现。它符合标准,具有许多高级功能,如可靠的事务和无读锁的并发性。 本指南演示了如何在Ubuntu 20.04服务器上快速启动和运行Postgres,从安装PostgreSQL到…...

IT程序员面试题目汇总及答案-计算机面试
程序员面试题目汇总及答案-计算机面试 问题1:请你描述一下你在过去的工作中遇到的一个技术难题,你是如何解决的? 答案1:在我之前的工作中,我遇到了一个涉及大数据处理的问题。由于数据量巨大,传统的处理方法无法在规定的时间内完成。我最后采用了一种分布式计算的方法,…...

【Flink on k8s】- 5 - 简要介绍 Flink
目录 1、了解流计算框架 1.1 分代 1.2 流计算框架对比 2、Flink 的应用场景 2.1 Data anal...

物联网安全芯片ACL16 采用 32 位内核,片内集成多种安全密码模块 且低成本、低功耗
ACL16 芯片是研制的一款32 位的安全芯片,专门面向低成本、低功耗的应用领域, 特别针对各类 USB KEY 和安全 SE 等市场提供完善而有竞争力的解决方案。芯片采用 32 位内核,片内集成多种安全密码模块,包括SM1、 SM2、SM3、 SM4 算法…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
