[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-6复数Complex Number
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-数学基础Ch0-6复数Complex Number
x 2 − 2 x + 2 = 0 ⇒ x = 1 ± i x^2-2x+2=0\Rightarrow x=1\pm i x2−2x+2=0⇒x=1±i
- 代数表达: z = a + b i , R e ( z ) = a , I m ( z ) = b z=a+bi,\mathrm{Re}\left( z \right) =a,\mathrm{Im}\left( z \right) =b z=a+bi,Re(z)=a,Im(z)=b, 分别称为
实部与虚部 - 几何表达: z = ∣ z ∣ cos θ + ∣ z ∣ sin θ i = ∣ z ∣ ( cos θ + sin θ i ) z=\left| z \right|\cos \theta +\left| z \right|\sin \theta i=\left| z \right|\left( \cos \theta +\sin \theta i \right) z=∣z∣cosθ+∣z∣sinθi=∣z∣(cosθ+sinθi)

- 指数表达: z = ∣ z ∣ e i θ z=\left| z \right|e^{i\theta} z=∣z∣eiθ
z 1 = ∣ z 1 ∣ e i θ 1 , z 2 = ∣ z 2 ∣ e i θ 2 ⇒ z 1 ⋅ z 2 = ∣ z 1 ∣ ∣ z 2 ∣ e i ( θ 1 + θ 2 ) z_1=\left| z_1 \right|e^{i\theta _1},z_2=\left| z_2 \right|e^{i\theta _2}\Rightarrow z_1\cdot z_2=\left| z_1 \right|\left| z_2 \right|e^{i\left( \theta _1+\theta _2 \right)} z1=∣z1∣eiθ1,z2=∣z2∣eiθ2⇒z1⋅z2=∣z1∣∣z2∣ei(θ1+θ2)

共轭: z 1 = a 1 + b 1 i , z 2 = a 2 − b 2 i ⇒ z 1 = z ˉ 2 z_1=a_1+b_1i,z_2=a_2-b_2i\Rightarrow z_1=\bar{z}_2 z1=a1+b1i,z2=a2−b2i⇒z1=zˉ2

相关文章:

[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-6复数Complex Number
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-数学基础Ch0-6复数Complex Number x 2 − 2 x 2 0 ⇒ x 1 i x^2-2x20\Rightarrow x1\pm i x2−2x20⇒x1i 代数表达: z a b i , R e ( z ) a , I m ( z ) b zabi,\mathrm{Re}…...

使用 MITRE ATTCK® 框架缓解网络安全威胁
什么是MITRE ATT&CK框架 MITRE Adversarial Tactics, Techniques, and Common Knowledge(ATT&CK)是一个威胁建模框架,用于对攻击者用来入侵企业、云和工业控制系统(ICS)并发起网络攻击…...
)
从零构建属于自己的GPT系列4:模型训练3(训练过程解读、序列填充函数、损失计算函数、评价函数、代码逐行解读)
🚩🚩🚩Hugging Face 实战系列 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在PyCharm中进行 本篇文章配套的代码资源已经上传 从零构建属于自己的GPT系列1:数据预处理 从零构建属于自己的GPT系列2:模型训…...

光学遥感显著目标检测初探笔记总结
目录 观看地址介绍什么是显著性目标检测根据不同的输入会有不同的变体(显著性目标检测家族)目前这个领域的挑战 技术方案论文1(2019)论文2(2021)论文3(2022) 未来展望 观看地址 b站链接 介绍 什么是显著性目标检测 一张图片里最吸引注意力的部分就是显著性物体,…...

HttpComponents: 领域对象的设计
1. HTTP协议 1.1 HTTP请求 HTTP请求由请求头、请求体两部分组成,请求头又分为请求行(request line)和普通的请求头组成。通过浏览器的开发者工具,我们能查看请求和响应的详情。 下面是一个HTTP请求发送的完整内容。 POST https://track.abc.com/v4/tr…...

使用wire重构商品微服务
一.wire简介 Wire 是一个轻巧的Golang依赖注入工具。它由Go Cloud团队开发,通过自动生成代码的方式在编译期完成依赖注入。 依赖注入是保持软件 “低耦合、易维护” 的重要设计准则之一。 此准则被广泛应用在各种开发平台之中,有很多与之相关的优秀工…...

大三上实训内容
项目一:爬取天气预报数据 【内容】 在中国天气网(http://www.weather.com.cn)中输入城市的名称,例如输入信阳,进入http://www.weather.com.cn/weather1d/101180601.shtml#input 的网页显示信阳的天气预报,其中101180601是信阳的…...

IOT安全学习路标
1. 物联网基础知识 首先,你需要建立坚实的物联网基础知识,包括IoT的架构和组件,传感器和设备的连接和通信技术,云端和边缘计算等。 2. 通信和网络安全 学习关于物联网通信和网络安全的基础知识,包括加密和认证技术、…...

java中线程的状态是如何转换的?
在 Java 中,线程有几种状态,主要包括 NEW(新建)、RUNNABLE(可运行)、BLOCKED(阻塞)、WAITING(等待)、TIMED_WAITING(计时等待)、和 TE…...

处理合并目录下的Excel文件数据并指定列去重
处理合并目录下的Excel文件数据并指定列去重 需求:读取指定目录下的Excel文件并给数据做合并与去重处理 Python代码实现 import os import pandas as pd import warnings import time from tqdm import tqdm #进度条展示def read_excel(path):dfs []for file in…...

Numpy数组的去重 np.unique()(第15讲)
Numpy数组的去重 np.unique()(第15讲) 🍹博主 侯小啾 感谢您的支持与信赖。☀️ 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ�…...

ROS-log功能区别
ROS使用rosout包来记录各个节点的log信息,通常这些log信息是一些可以读懂的字符串信息,这些信息一般用来记录节点的运行状态。 ROS有五种不同类型的log信息,分别为:logdebug、loginfo、logwarn、logerr、logfatal。 等级由低到高&…...

学习git后,真正在项目中如何使用?
文章目录 前言下载和安装Git克隆远程仓库PyCharm链接本地Git创建分支修改项目工程并提交到本地仓库推送到远程仓库小结 前言 网上学习git的教程,甚至还有很多可视化很好的git教程,入门git也不是什么难事。但我发现,当我真的要从网上克隆一个…...
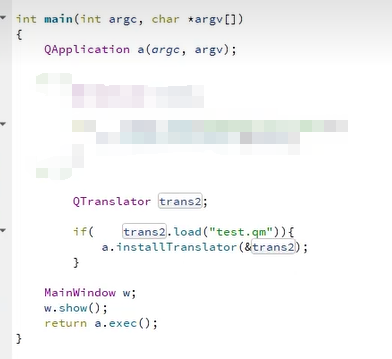
Qt国际化翻译Linguist使用
QT的国际化是非常方便的,简单的说就是QT有自带的翻译工具把我们源代码中的字符串翻译成任何语言文件,再把这个语言文件加载到项目中就可以显示不同的语言。下面直接上手: 步骤一:打开pro文件,添加:TRANSLA…...

ShardingSphere数据分片之分表操作
1、概述 Apache ShardingSphere 是一款分布式的数据库生态系统, 可以将任意数据库转换为分布式数据库,并通过数据分片、弹性伸缩、加密等能力对原有数据库进行增强。 Apache ShardingSphere 设计哲学为 Database Plus,旨在构建异构数据库上…...
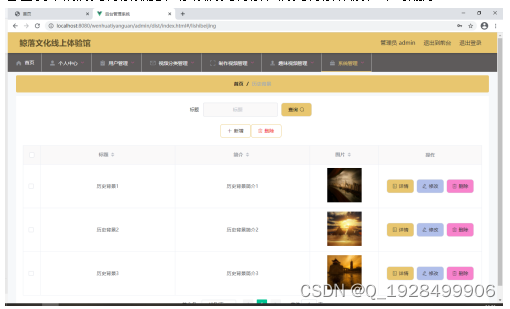
基于ssm鲸落文化线上体验馆论文
摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本鲸落文化线上体验馆就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕庞大的数据信…...

LeetCode Hot100 131.分割回文串
题目: 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。 回文串 是正着读和反着读都一样的字符串。 方法:灵神-子集型回溯 假设每对相邻字符之间有个逗号,那么就看…...
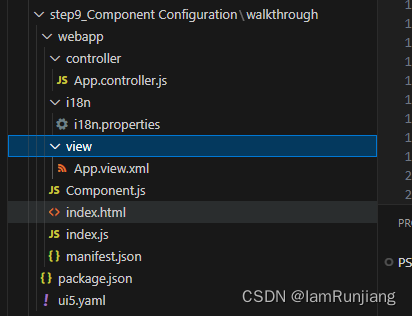
SAP UI5 walkthrough step9 Component Configuration
在之前的章节中,我们已经介绍完了MVC的架构和实现,现在我们来讲一下,SAPUI5的结构 这一步,我们将所有的UI资产从index.html里面独立封装在一个组件里面 这样组件就变得独立,可复用了。这样,无所什么时候我…...
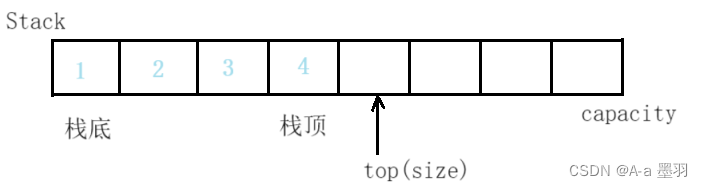
【数据结构和算法】--- 栈
目录 栈的概念及结构栈的实现初始化栈入栈出栈其他一些栈函数 小结栈相关的题目 栈的概念及结构 栈是一种特殊的线性表。相比于链表和顺序表,栈只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的…...

CentOS7.0 下rpm安装MySQL5.5.60
下载 下载路径: MySQL :: Download MySQL Community Server -->looking for the latest GA version-->5.5.60 此压缩包中有多个rpm包 有四个不是必须的,只需安装这三个 MySQL-server-5.5.60-1.el6.x86_64 MySQL-devel-5.5.60-1.el6.x86_64 MySQL-client-5.5.60-1.el6.x8…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
