暴力递归到动态规划
暴力递归到动态规划
假设有排成一行的n个位置, 记为1~n,n-定大于或等于2。开始时机器人在其中的m位置上(m 一定是1~n中的一个)。如果机器人来到1位置,那么下一步只能往右来到2位置;如果机器人来到n位置, 那么下一步只能往左来到n-1位置;如果机器人来到中间位置,那么下一步可以往左走或者往右走;规定机器人必须走k步,最终能来到p位置(p也是1~n中的一个)的方法有多少种?给定四个参数n、m、k、p,返回方法数。
暴力递归
public static int robot(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;return walk(n, m, k, p);
}// n 还是表示一共n个位置,p 还是表示目标位置
// cur 表示当前位置,rest表示还能走几步
private static int walk(int n, int cur, int rest, int p) {// 如果没有剩余步数了,当前的cur位置就是最后的位置// 如果最后的位置停在P上,那么之前做的移动是有效的// 如果最后的位置没在P上,那么之前做的移动是无效的if (rest == 0)return cur == p ? 1 : 0;if (cur == 1)return walk(n, cur + 1, rest - 1, p);if (cur == n)return walk(n, cur - 1, rest - 1, p);// 如果还有rest步要走,而当前的cur位置在中间位置上,那么当前这步可以走向左,也可以走右// 走向左之后,后续的过程就是,来到cur-1位置 上,还剩rest-1步要走// 走向右之后,后续的过程就是,来到cur+1位置. 上,还剩rest-1步要走// 走向左、走向右是截然不同的方法,所以总方法数要都算上return walk(n, cur - 1, rest - 1, p) + walk(n, cur + 1, rest - 1, p);
}
这种解法是最纯粹的暴力递归,有一些是重复计算。可以发现递归时只有两个参数对结果有实际影响
当前位置 剩余步数 ,如果将这两个参数的取值组成一张矩阵,计算好的数据存在矩阵中,当碰到有重复计算时只需要取值即可。
半动态规划
// 上述的这种暴力递归方法是有重复计算的。可以看出递归中n、p两个参数是固定不变的,结果只取决于(m,k)的组合,如果有
// 一个cache存放各种组合的结果,当重复计算时只需要从cache中返回结果。
public static int robotCache(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;int[][] cache = new int[n + 1][k + 1];// 默认将cache所有元素都设为-1,表示从来没计算过,当递归访问某个元素时发现不是-1时说明已经计算过了,直接取值即可for (int[] ints : cache) Arrays.fill(ints, -1);return walkCache(n, m, k, p, cache);
}// 此时,所有的递归都要带上cache这张表一起玩
private static int walkCache(int n, int cur, int rest, int p, int[][] cache) {if (cache[cur][rest] != -1)return cache[cur][rest];if (rest == 0){cache[cur][rest] = cur == p ? 1 : 0;return cache[cur][rest];}if (cur == 1){cache[cur][rest] = walkCache(n, cur + 1, rest - 1, p, cache);return cache[cur][rest];}if (cur == n){cache[cur][rest] = walkCache(n, cur - 1, rest - 1, p, cache);return cache[cur][rest];}// 在中间位置cache[cur][rest] = walkCache(n, cur - 1, rest - 1, p, cache) +walkCache(n, cur + 1, rest - 1, p, cache);return cache[cur][rest];
}
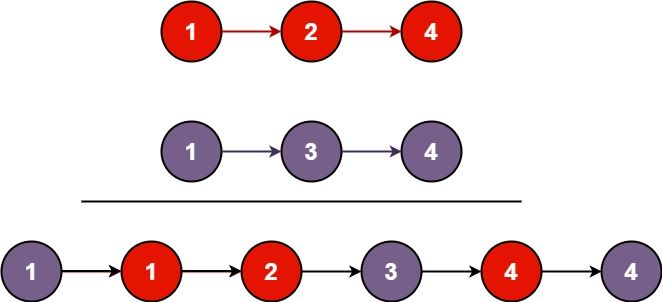
通过分析发现,当cur=1cur=1cur=1 时,依赖 cache[cur+1][rest−1]cache[cur+1][rest-1]cache[cur+1][rest−1] 的值;当 cur=ncur=ncur=n 时,依赖 cache[cur−1][rest−1]cache[cur-1][rest-1]cache[cur−1][rest−1] 的值;当cur不在首尾时,依赖 cache[cur−1][rest−1]cache[cur-1][rest-1]cache[cur−1][rest−1] 和 cache[cur+1][rest−1]cache[cur+1][rest-1]cache[cur+1][rest−1] 。没有cur=0cur=0cur=0 的情况,虽然cache容量为(N+1)×(K+1)(N+1) \times (K+1)(N+1)×(K+1) ,但那是为了方便运算而已。初始情况下,rest=0rest=0rest=0,如果cur≠pcur \neq pcur=p 则为0,否则为1。假设目标位置p=3p=3p=3 如下图所示:
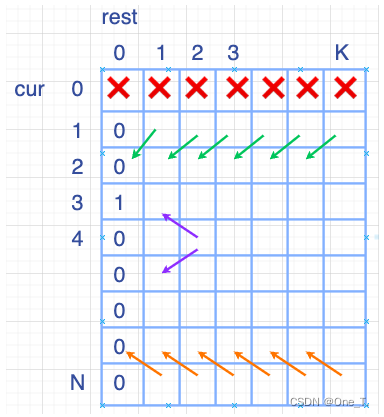
如果确定了这种依赖关系后,直接填表就好了,连递归都省了。
纯粹动态规划
public static int dp(int n, int m, int k, int p){// 无效参数的情况if (n < 2 || m < 1 || m > n || k < 1 || p < 1 || p > n)return 0;int[][] cache = new int[n + 1][k + 1];cache[p][0] = 1;// 先填列再填行for (int col = 1; col < cache[0].length; col++) {for (int row = 1; row < cache.length; row++) {if (row == 1)cache[row][col] = cache[row + 1][col - 1];else if (row == cache.length - 1)cache[row][col] = cache[row - 1][col - 1];elsecache[row][col] = cache[row - 1][col - 1] + cache[row + 1][col - 1];}}return cache[m][p];
}
相关文章:

暴力递归到动态规划
暴力递归到动态规划 假设有排成一行的n个位置, 记为1~n,n-定大于或等于2。开始时机器人在其中的m位置上(m 一定是1~n中的一个)。如果机器人来到1位置,那么下一步只能往右来到2位置;如果机器人来到n位置, 那么下一步只能…...

Java:Java仍然处于领先地位?
没有多少编程语言能够自吹自擂并持续流行20多年,但Java就是其中之一。Java应用程序不仅局限于web和移动开发,而且给大数据和人工智能留下了深刻的印象。不用多说,让我们讨论一下Java流行的几个原因!!1.实用性根据JamesGosling的说法ÿ…...
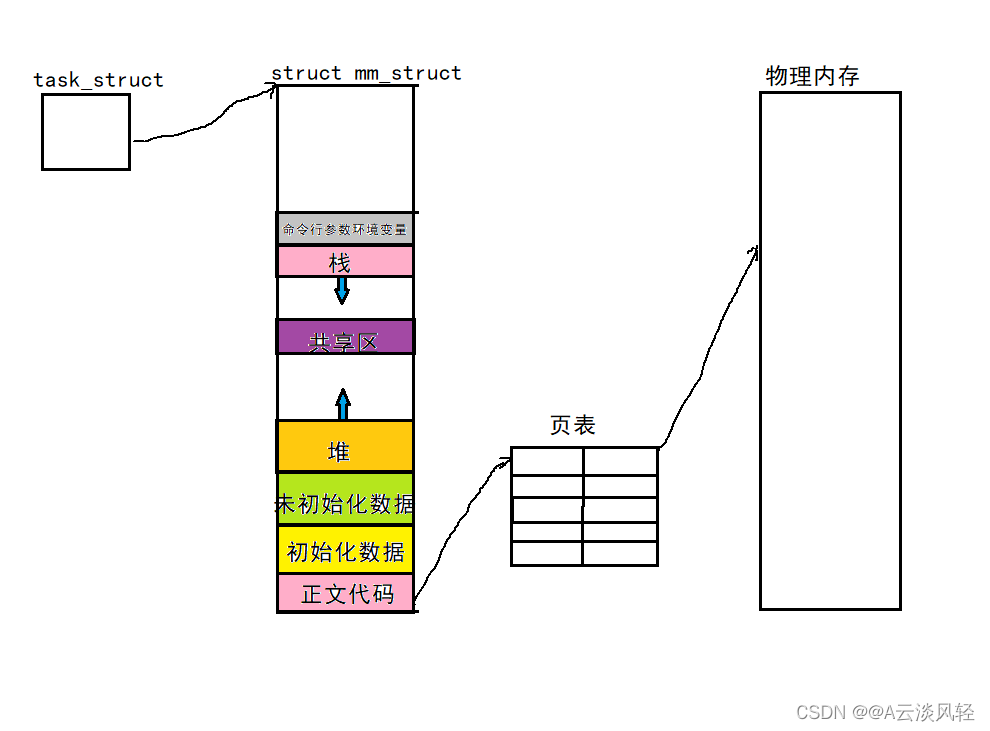
虚拟地址空间
本节目录1.如何理解区域划分2.为什么一个变量可以存储两个不同的值?3.深入理解虚拟地址空间为什么要有地址空间?4.理解什么是挂起?1.虚拟地址空间究竟是什么?2.映射关系的维护是谁做的?1.如何理解区域划分 所谓的区域…...
Python基础篇(十五)-- Pygame游戏编程
1 初识Pygame Pygame是一个开源的Python模块,专门用于多媒体应用(如电子游戏)的开发,其中包含对图像、声音、视频、事件、碰撞等的支持。Pygame建立在SDL的基础上,SDL是一套跨平台的多媒体开发库,用C语言实…...
LeetCode 热题 HOT 100 Java 题解 -- Part 2
练习地址 Part 1 : https://blog.csdn.net/qq_41080854/article/details/128829494 LeetCode 热题 HOT 100 Java 题解 -- Part 236. 二叉树的中序遍历 9437. 不同的二叉搜索树 9638. 验证二叉搜索树 9839. 对称二叉树 10140. 二叉树的层序遍历 10241. 二叉树的最大深度 10442.…...
【项目实战】IDEA常用快捷键汇总
一、修改为Eclipse的快捷键 相信很多朋友跟我一样, 都是习惯了eclipse的快捷键,没错,习惯这东西真的很难改!IDEA非常强大,支持我们修改IDEA中的keymap为Eclipse的快捷键!友好又贴心,有没有&…...
更新 TKK 失败,请检查网络连接。谷歌翻译 translation插件不能用解决办法 亲测有效
谷歌翻译无法使用,谷歌回应解释是,谷歌翻译使用率过低,所以选择停止服务。网上也有说法,指出根本原因为,提供API接口的googleapis被墙,这导致js文件和字体资源无法加载。 这里提供两种解决办法 方案一 修…...

SpringBoot整合MybatisPlus多数据源
相信在很多使用MybatisPlus框架的小伙伴都会遇到多数据源的配置问题,并且官网也给出了推荐使用多数据源 (dynamic-datasource-spring-boot-starter) 组件来实现。由于最近项目也在使用这个组件来实现多数据源切换,因此想了解一下该组件是如何运行的&…...

【教程】如何使用Java生成PDF文档?
在如今数字化时代,越来越多的人使用PDF文档进行信息传递和共享。而使用Java生成PDF文档也成为了一个非常重要的技能,因为Java作为一种通用的编程语言,可以在不同的操作系统和平台上运行。下面,我们将为您介绍如何使用Java生成PDF文…...
I.MX6ULL内核开发13:pinctrl子系统和gpio子系统-led实验
目录 一、pinctrl子系统 1.1 pinctrl子系统编写格式以及引脚属性介绍 1.1.1 iomux节点介绍 1.1.2 pinctrl子节点编写格式 1.1.3 引脚配置信息介绍 1.2 将RGB灯引脚添加到pinctrl子系统 1.2.1 查找RGB灯使用的引脚 1.2.2找到引脚宏定义 1.2.3 设置引脚属性 1.2.4 在…...

Linux系列 使用vi文本编辑器
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.vi文本编辑器 1.使用vi文本编辑器 2.vi编辑器的工作模式 3.命令模式中的…...
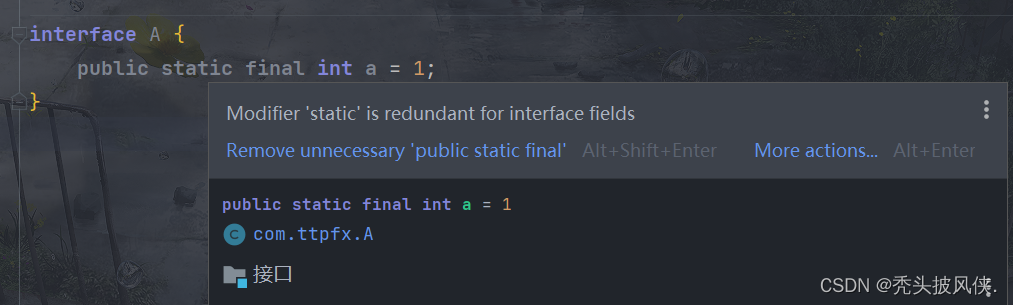
【java基础】接口(interface)
文章目录基础介绍接口的定义关于接口字段和方法的说明使用接口抽象类和接口接口方法冲突的一些说明方法相同名称和参数,返回值相同方法名称相同,参数不同,返回值相同方法返回值不同,名称参数相同方法完全相同,一个有默…...

ChatGPT(GPT3.5) OpenAI官方API正式发布
OpenAI社区今天凌晨4点多发送的邮件,介绍了ChatGPT官方API的发布。官方介绍文档地址为“OpenAI API”和“OpenAI API”。 ChatGPT(GPT3.5)官方API模型名称为“gpt-3.5-turbo”和“gpt-3.5-turbo-0301”。API调用价格比GPT text-davinci-003模型便宜10倍。调用费用为…...
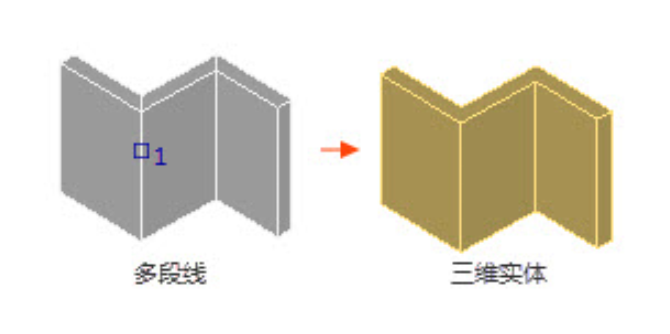
CAD中如何将图形对象转换为三维实体?
有些小伙伴在CAD绘制完图纸后,想要将图纸中的某些图形对象转换成三维实体,但却不知道该如何操作,其实很简单,本节CAD绘图教程就和小编一起来了解一下浩辰CAD软件中将符合条件的对象转换为三维实体的相关操作步骤吧! 将…...
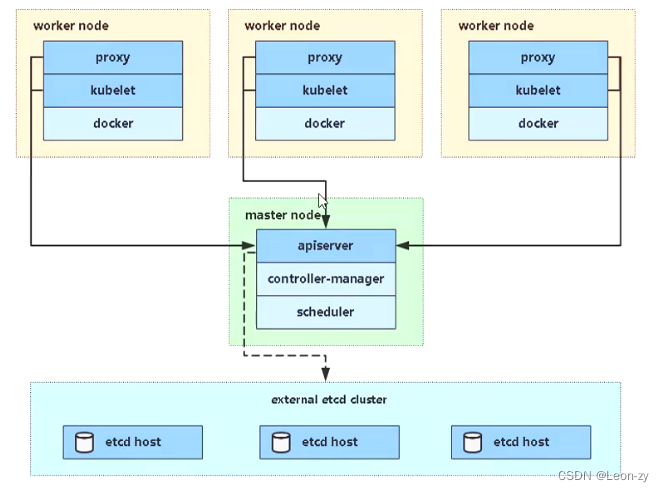
【K8S笔记】Kubernetes 集群架构与组件介绍
K8S 官方文档 https://kubernetes.io/zh/docs/home ##注重关注 概念和任务 板块。 K8S 集群架构 K8S也是运用了分布式集群架构: 管理节点/Master 整个集群的管理,任务协作。工作节点/Node 容器运行、删除。 K8S 组件介绍 管理节点/Master 相关组件 …...
9 怎么登录VNC
1)首先在ssh登录后启动vncserver。登陆后输入下面的指令来创建自己的VNC。 命令vncserver :16 –geometry 1900x1000 其中:16是分配的端口号,1900x1000是分辨率。如果没有响应,建议执行下面操作后再次重复上面操作。 命令…...
MPI ubuntu安装,mpicc,mpicxx,mpif90的区别
介绍 MPI是并行计算的一个支持库,支持对C、C、fortran语言进行并行计算。 安装基础环境 ubuntu进行gcc/g/gfortran的安装: gcc: ubuntu下自带gcc编译器。可以通过gcc -v命令来查看是否安装。 g: sudo apt-get install buil…...

移动端笔记
目录 一、移动端基础 二、视口 三、二倍图/多倍图 四、移动端开发 (一)开发选择 (二)常见布局 (三)移动端技术解决方案 五、移动WEB开发之flex布局 六、移动WEB开发之rem适配布局 #END(…...

操作系统笔记、面试八股(一)—— 进程、线程、协程
文章目录1. 进程、线程、协程1.1 进程1.1.1 进程间的通信方式1.1.2 进程同步方式1.1.3 进程的调度算法1.1.4 优先级反转1.1.5 进程状态1.1.6 PCB进程控制块1.1.7 进程的创建和撤销过程1.1.8 为什么要有进程1.2 线程1.2.1 为什么要有线程1.2.2 线程间的同步方式1.3 协程1.3.1 什…...
Python每日一练(20230302)
目录 1. 字符串统计 2. 合并两个有序链表 3. 下一个排列 附录 Python字典内置方法 增 删 改 查 其它 1. 字符串统计 从键盘输入一个包含有英文字母、数字、空格和其它字符的字符串,并分别实现下面的功能:统计字符串中出现2次的英文字母&#…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
