算法--最短路
这里写目录标题
- xmind
- 单源最短路
- 简介
- 所有边权都是正
- 朴素的Dijkstra算法
- 思想
- 例子+题解
- 堆优化版的Dijkstra算法
- 存在负数权
- Bellman-Ford算法
- 思想
- 例子+题解
- spfa算法
- 思想
- 例子+题解
- spfa判断负环
- 思想
- 例子+题解
- 多源汇最短路
- 简介
- 弗洛伊德算法
- 思想
- 例子+题解
- 小tips
xmind

上述中,朴素Dijkstra算法适用于稠密图
其他用堆优化版
而SPFA算法一般都比Bellman-Ford算法要快
Floyd没得选
稠密图和稀疏图的定义:

其中m是边数,n是点数
当m的数据量与n方一样或者更多,那么就是稠密图,如果m跟n数据量一样,或者说更少,那么就是稀疏图

最短路问题,只会考察如何抽象出问题并实现代码,并不会考察算法的原理,重点在于抽象以及代码的实现
单源最短路
简介
只有一个起点,到其他某个点的最短路
所有边权都是正
朴素的Dijkstra算法
思想

一些解释:
s数组存放目前已经确定的最短距离的点
第一步中:dis数组是某个点到原点的距离,初始化一号点(一号点就是源点,因为图论中结点的编号都是从1开始的)的dis数值为0,其他全为一个很大的数
第二步中:for 遍历i从0到n
对于每次循环
将不在s中的距离dis最近的点给到t
把t加到s
用t来更新其他所有点的距离,如上图,如果满足dis[x]>dis[t]+w(t到x的权值),那么更新dis[x]的值为dis[t]+w的值
因为该算法适用于稠密图,所以用邻接矩阵来存储图
例子+题解
(手动过滤自环和重边)



数据分析:n m分别是点数和边数
g数组存放某两个点的权值,例如g[a][b]=1,表示a与b之间的权值是1
dist数组用来存放某个点到原点也就是一号点的距离
st数组就是用来表示某个点的最短路已经被找到
dijkstra算法:
首先初始化dist为无穷大,用十六进制0x3f初始化即可
之后初始化dist[1]为0,因为一号点是源点
之后for循环,循环n次
首先初始化t为-1
之后,对于每个节点编号从1到n
if(某个点没有确定最短路,并且(t未被赋值,或者,j是没有确定最短路的最近的点即dist[t]>dist[j]) ),这时将j赋值给t
同时更新st[t]为true
然后对每个节点编号进行循环,用t更新其他结点的最短路
dist[j]=min(dist[j],dist[t]+g[t][j])
最后,如果dist某个点的距离仍然是0x3f(因为利用memset初始化是初始其值的四分之一即可,但是0,-1是初始化自己),那么返回-1,表示路径不存在
最后返回dist[n],这里根据具体的题目要求进行返回即可,因为题目让返回n号点

之所以取min,是因为该题存在自环和重边,如下:但是因为要求最短路,所以当某两个点有多个权值的时候,取权值最小的当做其权值,较大的权值就不看了

堆优化版的Dijkstra算法
(无需手动过滤自环和重边,算法自己过滤)
题目与上面的题一样

对于add算法:
idx表示当前e数组中的可用位置,将目标点的编号存入e[]数组中,并且用一个w数组来维护权值,同时头插法:ne[idx]=h[a],h[a]=idx++
(因为e数组就是用来存节点信息的,又因为e数组所存信息的结点都是一个节点的出边节点组成的链表,所以信息就是节点的编号,所以目标结点的编号都放在e[]数组里,发出结点的编号都在h数组,所以函数里都是h[a])
(要明确,这里所说的图中的结点只有结点编号以及某两个点的权值,没有具体的意义数字,比如一号点表示着某些意义,这是不存在的,如果有意义数组,那么极有可能没给编号,那么可以将意义数字当成编号处理)

首先是一个优先队列,其中第二第三个参数是用来改变默认排序,改成从大到小排列
用一个pari来维护一个结点编号以及该点到源点的距离
while循环条件队列不空
然后取出队头元素给到t(没有确定最短路径的点,且距离源点最近)
之后将队头元素出队
然后拿到t的编号以及到源点的距离
if(st[ver]是真),那么说明这是重边,countinue即可
之后,用t来更新其他结点的最短路径:
for循环中,遍历t结点的所有一级出边,对于每个子链结点,拿到其存在e数组中的编号之后给j
之后更新
之后出队j的pair:{dist[j],j}

存在负数权
Bellman-Ford算法
思想

上面的方框是算法过程,下面的圆是经过该算法之后出现的现象,即对于每个a,b:dist[b]<=dist[a]+w,俗称三角不等式

其中 第一个for循环的次数是有实际意义的,循环k次,表示最短路径最多经过不超过k条边到达目标点

例子+题解
(无需手动过滤自环和重边,算法自己过滤)

输出案例:3

数据分析:
backup数组是用来备份dist数组的
结构体用来存放某两个点以及两个点之间的距离
并用该结构体类型创建边数组
对于bellman-ford算法
首先初始化dist数组
之后因为题目要求最多不超过k条边,所以循环k次
在k次循环的每次循环时,首先备份dist到backup数组
然后对于m条边,有m次循环,因为结构体来存放边,每个边是一个结构体元素,所以有几个边,就循环几次
之后利用结构体数组拿到每个边的数据,利用备份的a来更新dist[b]
最后如果n点(具体哪个点看题目要求)的dist>0x3f3f3f/2(记住就好),那么就表示没有最短路径
最后返回dist[n]

对于为什么要备份,如下:

因为有k条边的限制,所以,不能向之前那样,一个接着一个更新,这样的话,就会无视k条边的限制,直接找到没有限制的最短路径

利用备份的数据进行更新,每次都是最初版本的数据,都是正无穷,所以,不会发生数据更新,就会被限制到
spfa算法
思想
适用于没有负权回路

spfa算法是对Dijkstra算法的优化,优化的是上面打勾的那一步的处理
之前Dijkstra算法对于更新dist[b]的思路是,不管三七二十一遍历寻找t去更新dist[b]
这里spfa对dist[a]或者说t,对其进行判断是否被更新,如果被更新了才能去更新别的点,同时队列里只存放已经被更新的结点,拿着队列中已经被更新的点去更新其他点,才能有效
例子+题解
(无需手动过滤自环和重边,算法自己过滤)


spfa算法与Dijkstra算法差不多,唯一不同的是函数是Dijkstra函数改成spfa函数

数据分析,nm仍然是n个点,m条边
之后h数组w数组e数组ne数组idx都是用来构建邻接表
dist表示某个点到原点的距离
而这里不同于Dijkstra算法,st数组表示某号结点是否在队列中,例如st[2],表示二号点已经在队列中

spfa算法:
首先初始化dist,并初始化dist[1]=0
然后定义一个队列,元素为int
该队列用来存放那些已经被更新的结点,哪些编号的点已经被更新
一号已经更新,入队
之后while(队列不空){
取出队头元素编号,用t接住;
之后队头出队
将t编号的状态改为false,因为t已经出队了
之后遍历t的所有子链,即所有一级出边节点,通过e数组拿到编号,
之后看能否用t进行更新,如果可以,则更新,同时判断j点是否在队列,不在的话,就入队,并将st数组改为true
}
最后有返回值,根据具体情况来定,如下图:


spfa判断负环
思想

我们在更新dist数组时,维护一个cnt数组,表示从某个点到源点的最短路上一共有多少条边,
每次更新dist时,说明有更新,更新的是从源点到t之后再加上从t到x,那么就是cnt[t]+1
一旦发现cnt[x]>=n,因为正常情况下应该是小于n的,那么一定存在一个负环,使得多出了一些边,所以cnt[x]>=n表示存在负环
例子+题解
(无需手动过滤自环和重边,算法自己过滤)

如下是利用spfa算法判断负环的整体算法,他是在spfa算法上做了一些修改,如下标注

数据方面,多一个维护数组:cnt[N]

之后在spfa函数中,首先while循环里那个虚框可以忽视(画错了)
在while循环里:
在dist更新代码下面,更新一下cnt[j]=cnt[t]+1;
同时判断如果(cnt[j]>=n),那么返回true,表示有负环
如果最后没有返回true,那么在最后返回false
“spfa函数里”到“while循环上面”的代码整体修改为下图:(因为题目要求求所有的负环,而不是以1为源点的负环,所以将所有点都放入队列)


多源汇最短路
简介
多个起点
弗洛伊德算法
思想

弗洛伊德算法是用邻接矩阵来存,g[i][j]表示从i点到j点的权值,或者没有权值:有边就是1,没边就是0
例子+题解
(手动过滤自环和重边)



数据分析:INF宏定义为1e9,表示无穷大
floyd函数,三重循环:
从k从1到n
i从1到n
j从1到n
并更新邻接矩阵

main函数里,第一个二重循环是在处理自环,将自环初始化为0,其余初始化为INF
之后的while循环里,是在初始重边,有重边时取最小的
之后调用floyd函数
第二个while函数是在处理输出,这里注意,if(d>INF / 2)那么表示没有最短路
小tips
数据量在某个时间复杂度的计算下,小于一千万,表示一秒之内可以出解
相关文章:

算法--最短路
这里写目录标题 xmind单源最短路简介所有边权都是正朴素的Dijkstra算法思想例子题解 堆优化版的Dijkstra算法 存在负数权Bellman-Ford算法思想例子题解 spfa算法思想例子题解 spfa判断负环思想例子题解 多源汇最短路简介弗洛伊德算法思想例子题解 小tips xmind 上述中ÿ…...

Linux 定时任务备份MySQL数据库
Linux 定时任务基本知识 crontab yum install crontabs (安装 crontabs) systemctl enable crond (设为开机启动) systemctl start crond(启动crond服务) systemctl status crond (查看状态&a…...

查询服务器CPU、内存、磁盘、网络IO、队列、数据库占用空间等等信息
文章目录 摘要1. 查询CPU使用率命令:top -bn1 | grep \"Cpu(s)\" | awk {split($0,arr,\" \");print 100-arr[8]}2. 查询内存命令(单位:G):top -bn1 | grep \"KiB Mem\" | awk {split($…...
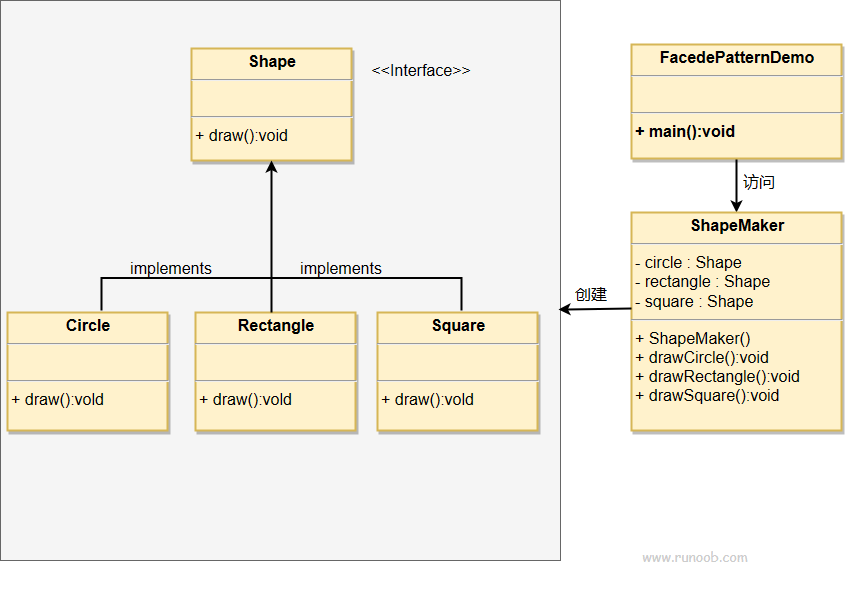
外观模式 rust和java的实现
文章目录 外观模式介绍实现javarustrust仓库 外观模式 外观模式(Facade Pattern)隐藏系统的复杂性,它为子系统中的一组接口提供一个统一的高层接口,使得这些接口更加容易使用。外观模式通过封装子系统内部的复杂性,提…...
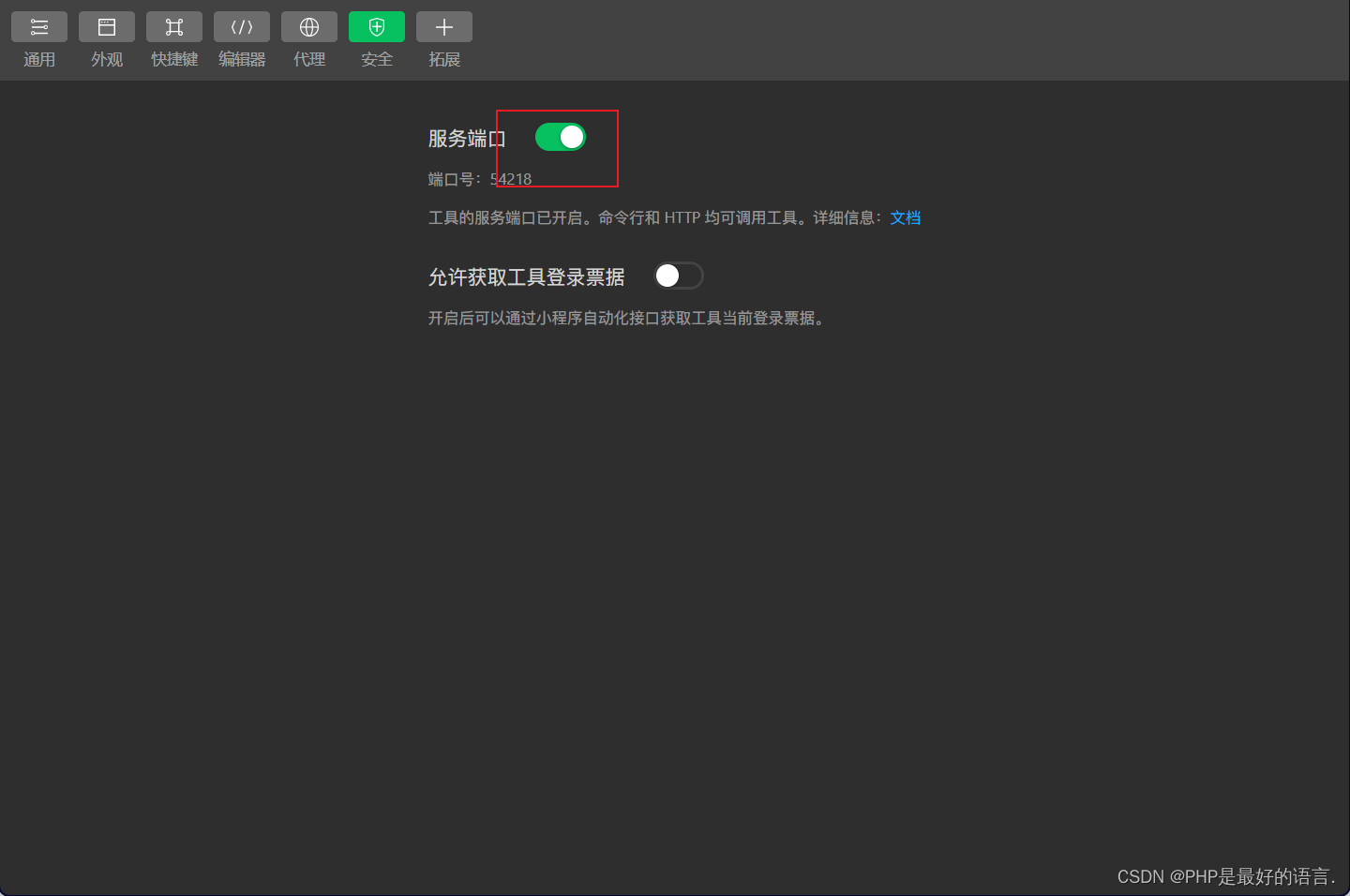
uniapp-hubildx配置
1.配置浏览器 (1)运行》运行到浏览器配置》配置web服务器 (2)选择浏览器安装路径 (3)浏览器安装路径: (3.1) 右键点击图标》属性 (3.2)选择目标&…...

Nginx基础篇:Nginx搭建、Nginx反向代理、文件服务器部署配置。
Nginx Linux系统安装以及反向代理的配置 简介优点nginx 环境安装常用Nginx 命令nginx 文件服务器搭建 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。Nginx是由伊戈尔赛索耶夫为俄罗斯访问量第二的Rambler.ru站点…...

什么是TDR(威胁检测与响应)
网络安全是被动和主动方法的混合体。过去,企业往往局限于被动的方法,随着合规性和安全策略越来越受到重视,主动方法也越来越受到关注。与其他行业相比,网络安全是高度动态的,网络安全团队采用任何可以帮助他们优化的新…...

30、pytest入门内容回顾
整体结构 解读与实操 pytest30讲主要从四个方面由浅入深的进行解读, 开始 讲解了pytest的概述,安装前的准备工作(python,pycharm,pytest),运行方式(命令行),断言(assert…...
2023年 - 我的程序员之旅和成长故事
2023年 - 我的程序员之旅和成长故事 🔥 1.前言 大家好,我是Leo哥🫣🫣🫣,今天咱们不聊技术,聊聊我自己,聊聊我从2023年年初到现在的一些经历和故事,我也很愿意我的故事分…...

JMH性能测试
一、JMH JMH,全称Java Microbenchmark Harness(微基准测试框架),是专门用于Java代码微基准测试的一套测试工具API,是由Java虚拟机团队开发的,一般用于代码的性能调优。 BenchMark又叫做基准测试,…...
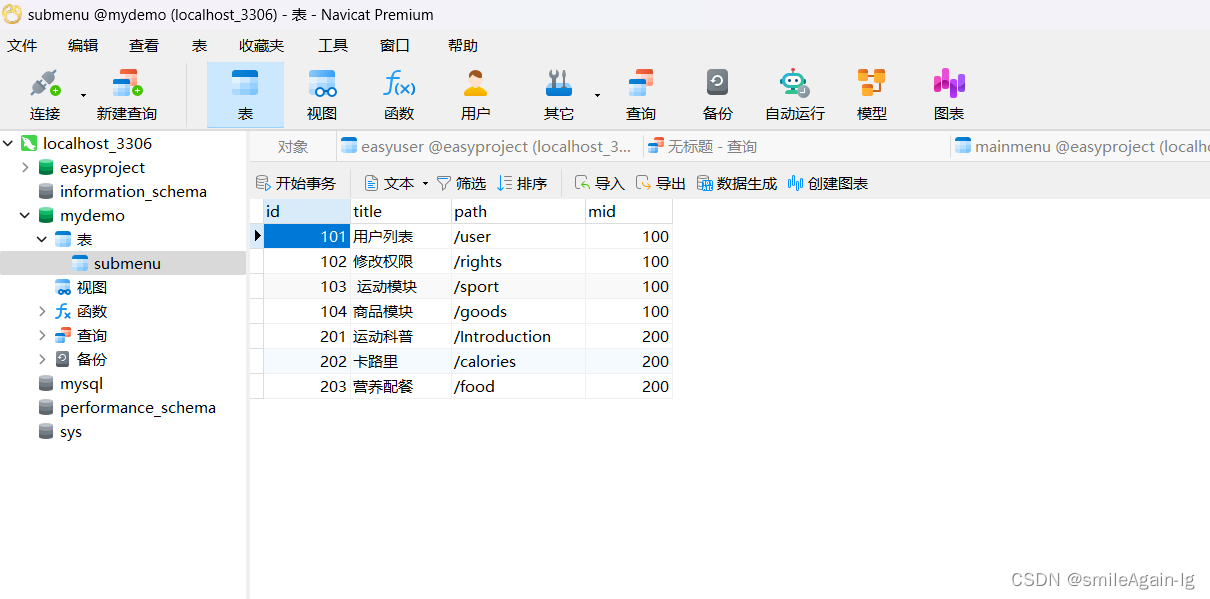
超完整的mysql安装配置方法(包含idea和navicat连接mysql,并实现建表)
mysql安装配置方法 1、下载mysql2、解压到指定的安装目录3、配置初始化文件my.ini4、配置用户变量和系统变量5、初始化mysql6、安装mysql服务并启动修改密码7、使用idea连接mysql8、使用Navicat可视化工具连接mysql,并实现新建数据库,新建表 1、下载mysq…...

通过仿真理解完整的阵列信号噪声模型
概要 噪声对无线电设备的信号接收会造成影响,是通信、雷达、导航、遥感等工程应用领域中的关键考虑因素。通常认为阵列合成能够提升信噪比,但忽略了这一论断的前提,即不同通道引入的噪声互不相关。但实际应用中,接收的噪声不仅仅包含信道引入的不相关噪声,还包含从外界环…...

问题:数组对象去重
问题:数组对象去重 var arr [{name: ‘a’,id: 1}, {name: ‘a’,id: 2}, {name: ‘b’,id: 3}, {name: ‘c’,id: 4}, {name: ‘c’,id: 6}, {name: ‘b’,id: 6}, {name: ‘d’,id: 7}]; 对数组对象name进行去重处理, 结果显示为: [{name…...

前端:让一个div悬浮在另一个div之上
使用 CSS 的 position 属性和 z-index 属性 首先,将第二个 div 元素的 position 属性设为 relative 或 absolute。这样可以让该元素成为一个定位元素,使得后代元素可以相对于它进行定位。 然后,将要悬浮的 div 元素的 position 属性设为 ab…...

千锋 Vue 详细笔记整理
视频笔记是根据B站 千锋 涛哥 - SpringBootvue前后端分离项目《锋迷商城》实战课-完结版 进行整理的 笔记可上 gitee仓库 自取 千锋 Vue 笔记整理 一、vue 的简介1.1 使用 JQuery 的复杂性问题1.2 VUE 简介1.2.1 前端框架1.2.2 MVVM 二、 vue 入门使用2.1 vue 的引入2.2 入门案…...
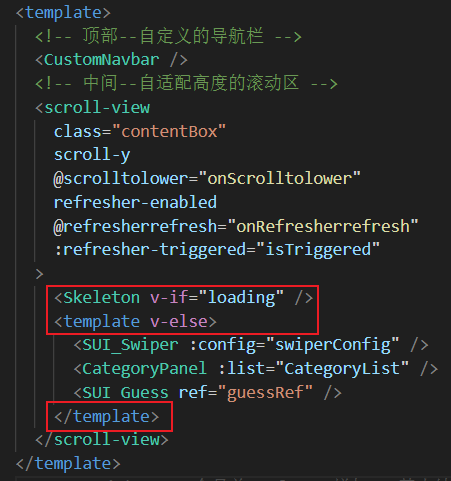
uniapp实战 —— 骨架屏
1. 自动生成骨架屏代码 在微信开发者工具中,预览界面点击生成骨架屏 确定后,会自动打开骨架屏代码文件 pages\index\index.skeleton.wxml 2. 将骨架屏代码转换为vue文件 在项目中新建文件 src\pages\index\components\skeleton.vue 将pages\index\index…...

【数据仓库-10】-- 数据仓库、数据湖和湖仓一体对比
目录 1 数据仓库与数据库的对比 2 数据湖与数据仓库的对比 3 数据仓库、数据湖和湖仓一体...
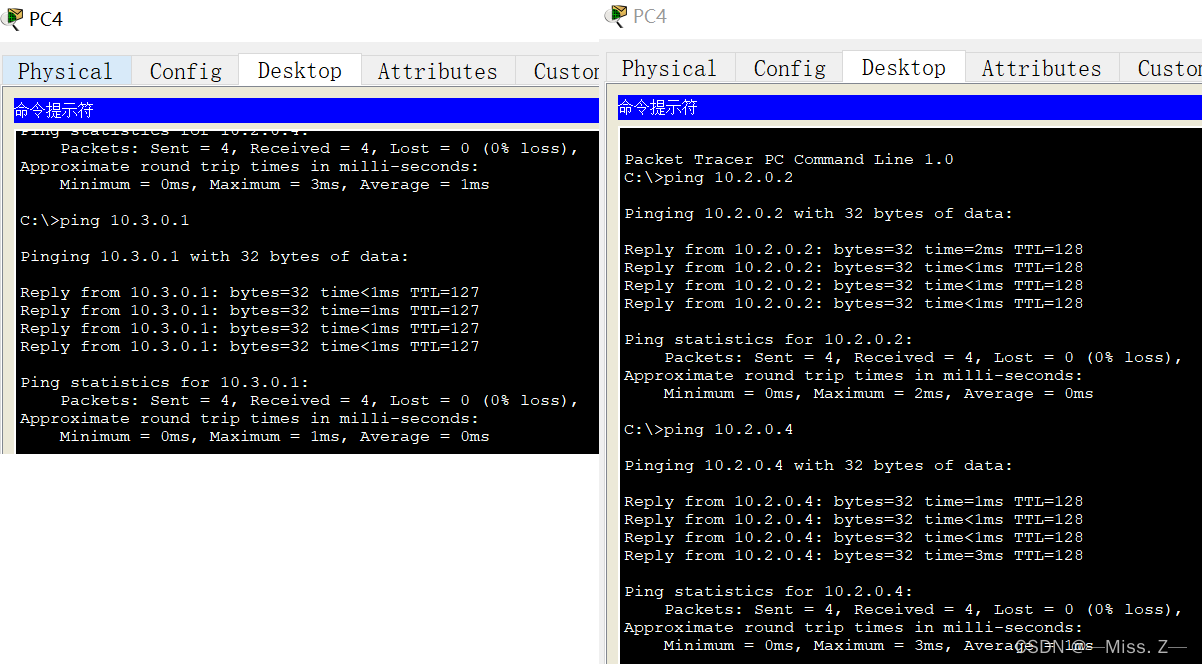
单臂路由与三层交换机
单臂路由 划分VLAN后同一VLAN的计算机属于同一个广播域,同一VLAN的计算机之间的通信是不成问题的。然而,处于不同VLAN的计算机即使是在同一交换机上,它们之间的通信也必须使用路由器。 图(a)是一种实现VLAN间路由的方…...

免费的数据采集软件,最新免费的几款数据采集软件【2024】
在当今数字化时代,数据是企业决策和业务发展的关键。而如何高效获取数据成为许多企业和研究机构的关注焦点。本文将深入探讨数据采集软件的种类。帮助大家选择最适合自己需求的数据采集工具。 数据采集软件种类 在众多数据采集软件中,有一类强大而多样…...
nodejs微信小程序+python+PHP北京地铁票务APP-计算机毕业设计推荐 -安卓
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
