线性回归实战
3.1 使用正规方程进行求解
3.1.1 简单线性回归
公式 :
y = w x + b y = wx + b y=wx+b
一元一次方程,在机器学习中一元表示一个特征,b表示截距,y表示目标值。
使用代码进行实现:
导入包
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(0, 10, num=30).reshape(-1, 1)
# 斜率和截距,随机生成
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)
# 根据一元一次方程计算目标值y并加上‘噪声’,数据有上下波动
y = X * w + b +np.random.rand(30,1)
plt.scatter(X,y)

# 计算斜率+截距
#系数
X = np.concatenate([X,np.full(shape=[30,1],fill_value=1)],axis=1)
X
获取系数
coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
w_ = coef_[0,0]
b_ = coef_[1,0]
print('正规方程算法计算,系数',w_,b_)
真实的系数
print('原始的数据斜率、截距',w,b)
绘制图形
plt.scatter(X[:,0],y,color='red')
plt.plot(X[:,0],X[:,0] * w_ + b_,color='green')
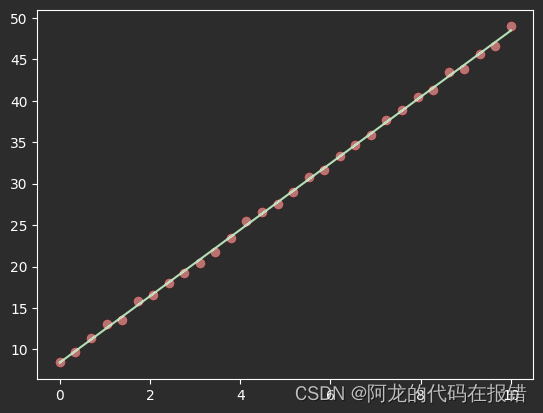
3.1.2 多元的线性回归
公式:
y = w 1 x 1 + w 2 x 2 + b y = w_1x_1 + w_2x_2 + b y=w1x1+w2x2+b
导入包
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像·
# 转化为矩阵
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))
# 斜率和截距,都是随机生成的
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)
# 根据二元一次方程计算目标值y 并且加上“噪声”,让数据上下波动
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) #三维散点图
ax.view_init(elev=10,azim=-20) # 调整视角
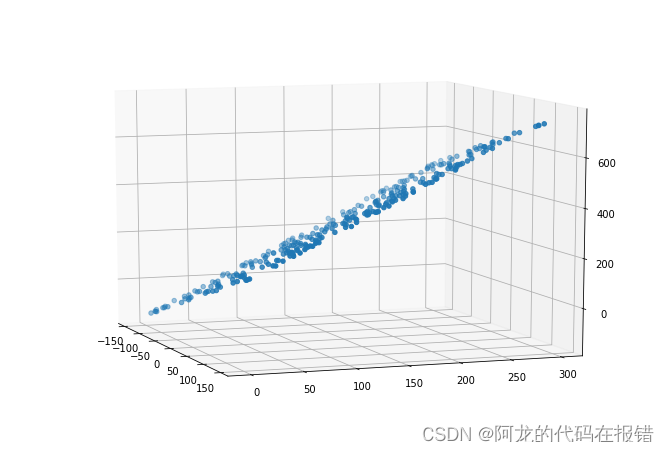
X = np.concatenate([x1,x2,np.full(shape=(300,1),fill_value=1)],axis = 1)
X
# 方程的系数
coef_ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
w1 = coef_[0][0]
w2 = coef_[1][0]
b_ = coef_[2][0]
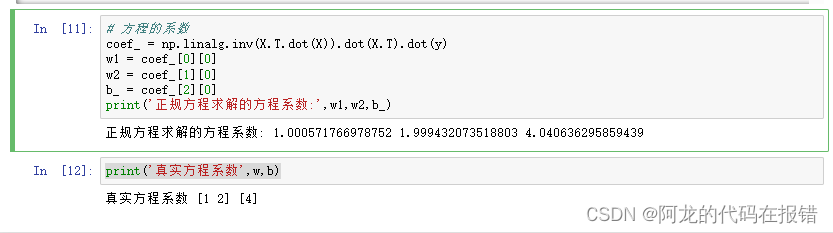
print('正规方程求解的方程系数:',w1,w2,b_)
print('真实方程系数',w,b)
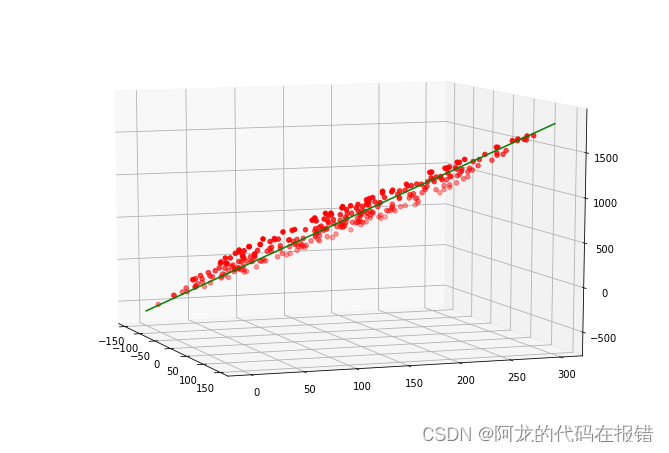
绘制拟合线段
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y,color='red') #三维散点图
ax.view_init(elev=10,azim=-20) # 调整视角
# 特征1:x1
x = np.linspace(-150,150,num=500)
y = np.linspace(0,300,num = 500)
z = x *w1_+ y*w2_ +b
ax.plot(x,y,z,color='green')

相关文章:

线性回归实战
3.1 使用正规方程进行求解 3.1.1 简单线性回归 公式 : y w x b y wx b ywxb 一元一次方程,在机器学习中一元表示一个特征,b表示截距,y表示目标值。 使用代码进行实现: 导入包 import numpy as np import matp…...

stm32 使用18B20 测试温度
用18b20 测试温度是非常常用的,不过18B20的调试不是这么容易的,有些内容网上很多的,不再重复说了,我先把波形说一下,再说程序部分: 整个都温度数据的顺序是: 1.700uS的低电平复位并测试18B20的…...
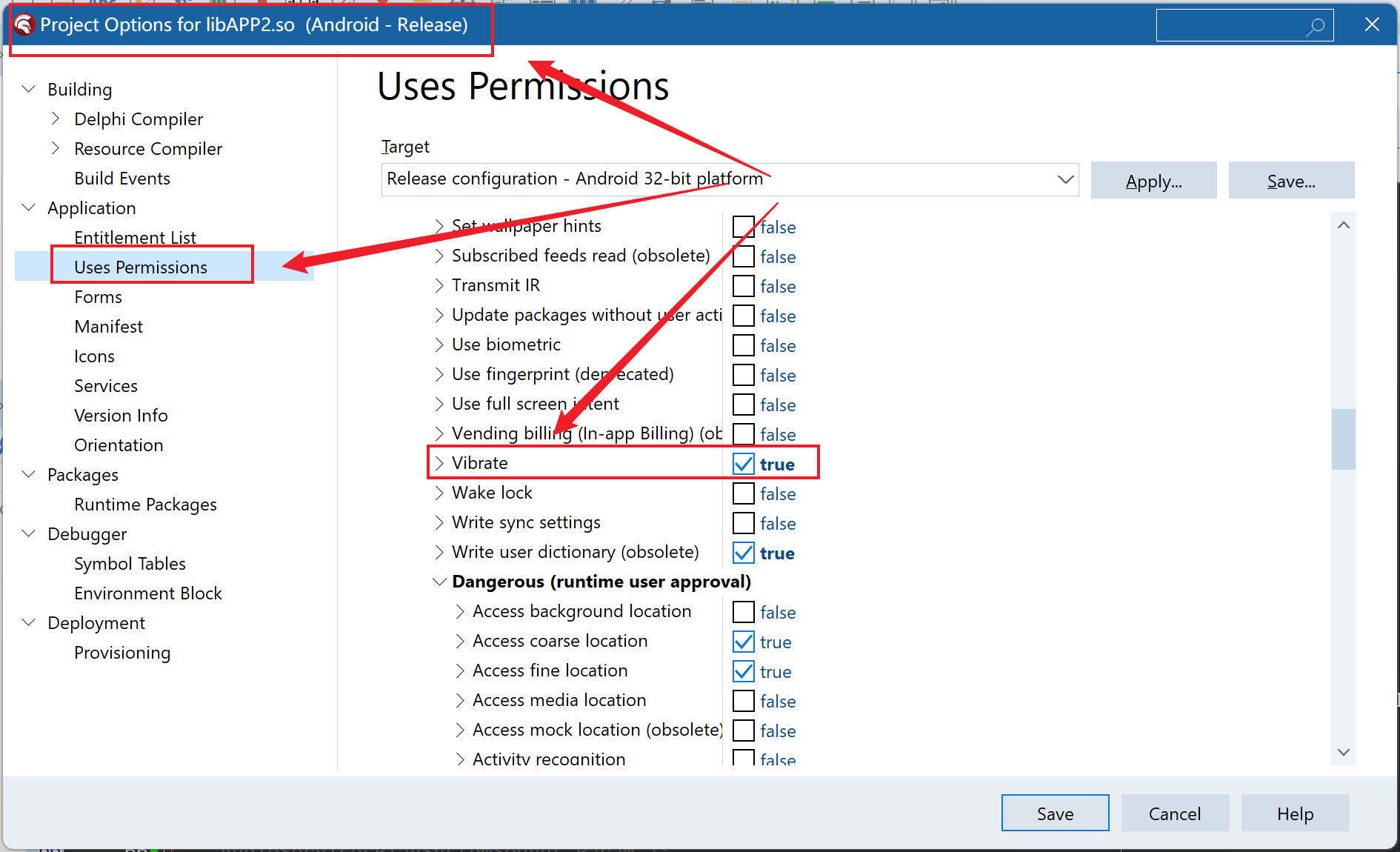
【Delphi】一个函数实现ios,android震动功能 Vibrate(包括3D Touch 中 Peek 震动等)
一、前言 我们在开发移动端APP的时候,有时可能需要APP能够提供震动功能,以便提醒操作者,特别是ios提供的3D Touch触感功能,操作者操作时会有触感震动,给操作者的感觉很友好。那么,在Delphi的移动端FMX开发中…...

国产Type-C PD芯片—接口快充取电芯片
常用USB PDTYPE-C受电端,即设备端协议IC芯片(PD Sink,也叫PD诱骗芯片),诱导取电芯片。 产品介绍 LDR6328: ◇ 采用 SOP-8 封装 ◇ 兼容 USB PD 3.0 规范,支持 USB PD 2.0 ◇ 兼容 QC 3.0 规范&#x…...
)
pytorch学习6-非线性变换(ReLU和sigmoid)
系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换(ReLU和sigmoid)pytorc…...

详解Keras3.0 Models API: Whole model saving loading
1、save方法 Model.save(filepath, overwriteTrue, **kwargs) 将模型另存为.keras文件 参数说明 filepath: 保存模型的路径。必须以.keras结尾overwrite:布尔值,表示是否覆盖已存在的文件。默认为 True,即覆盖已存在的文件。save_format…...
Spring Cloud Gateway 网关的基础使用
1. 什么是网关?网关有什么用? 在微服务架构中,网关就是一个提供统一访问地址的组件,它解决了内部微服务与外部的交互问题。网关主要负责流量的路由和转发,将外部请求引到对应的微服务实例上。同时提供身份认证、授权、…...
小米手机锁屏时间设置为永不休眠_手机不息屏_保持亮屏
环境:打开手机自带的锁屏时间设置发现没有 永不息屏的选项 原因:采用了三星OLED屏幕,所以根据OLED屏幕特性,这个是为了防止烧屏而特意设计的。非OLED机型支持设置“永不” 解决方案1:原生系统是支持永不锁屏的&#…...

lightdb plorasql集合类型新增可变数组
文章目录 背景集合类型可变数组可变数组示例 背景 在信创适配中,从Oracle迁移过来的存储过程使用到可变数组。因此在LightDB-X 23.4版本中对现有的集合类型进行了增强,添加了可变数组类型。 集合类型 在LightDB-X 23.4版本开始plorasql支持的集合类型…...

算法--最短路
这里写目录标题 xmind单源最短路简介所有边权都是正朴素的Dijkstra算法思想例子题解 堆优化版的Dijkstra算法 存在负数权Bellman-Ford算法思想例子题解 spfa算法思想例子题解 spfa判断负环思想例子题解 多源汇最短路简介弗洛伊德算法思想例子题解 小tips xmind 上述中ÿ…...

Linux 定时任务备份MySQL数据库
Linux 定时任务基本知识 crontab yum install crontabs (安装 crontabs) systemctl enable crond (设为开机启动) systemctl start crond(启动crond服务) systemctl status crond (查看状态&a…...

查询服务器CPU、内存、磁盘、网络IO、队列、数据库占用空间等等信息
文章目录 摘要1. 查询CPU使用率命令:top -bn1 | grep \"Cpu(s)\" | awk {split($0,arr,\" \");print 100-arr[8]}2. 查询内存命令(单位:G):top -bn1 | grep \"KiB Mem\" | awk {split($…...
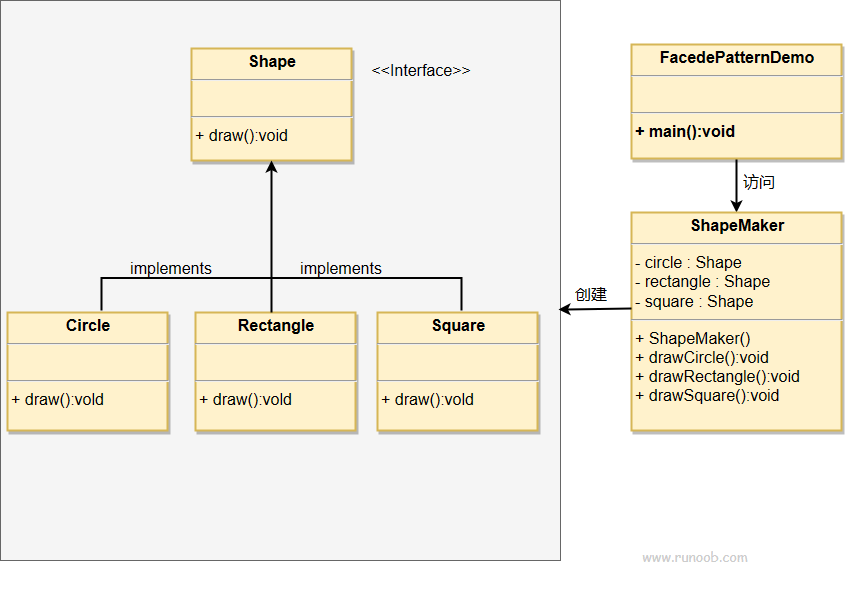
外观模式 rust和java的实现
文章目录 外观模式介绍实现javarustrust仓库 外观模式 外观模式(Facade Pattern)隐藏系统的复杂性,它为子系统中的一组接口提供一个统一的高层接口,使得这些接口更加容易使用。外观模式通过封装子系统内部的复杂性,提…...
uniapp-hubildx配置
1.配置浏览器 (1)运行》运行到浏览器配置》配置web服务器 (2)选择浏览器安装路径 (3)浏览器安装路径: (3.1) 右键点击图标》属性 (3.2)选择目标&…...

Nginx基础篇:Nginx搭建、Nginx反向代理、文件服务器部署配置。
Nginx Linux系统安装以及反向代理的配置 简介优点nginx 环境安装常用Nginx 命令nginx 文件服务器搭建 简介 Nginx (engine x) 是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。Nginx是由伊戈尔赛索耶夫为俄罗斯访问量第二的Rambler.ru站点…...

什么是TDR(威胁检测与响应)
网络安全是被动和主动方法的混合体。过去,企业往往局限于被动的方法,随着合规性和安全策略越来越受到重视,主动方法也越来越受到关注。与其他行业相比,网络安全是高度动态的,网络安全团队采用任何可以帮助他们优化的新…...

30、pytest入门内容回顾
整体结构 解读与实操 pytest30讲主要从四个方面由浅入深的进行解读, 开始 讲解了pytest的概述,安装前的准备工作(python,pycharm,pytest),运行方式(命令行),断言(assert…...
2023年 - 我的程序员之旅和成长故事
2023年 - 我的程序员之旅和成长故事 🔥 1.前言 大家好,我是Leo哥🫣🫣🫣,今天咱们不聊技术,聊聊我自己,聊聊我从2023年年初到现在的一些经历和故事,我也很愿意我的故事分…...

JMH性能测试
一、JMH JMH,全称Java Microbenchmark Harness(微基准测试框架),是专门用于Java代码微基准测试的一套测试工具API,是由Java虚拟机团队开发的,一般用于代码的性能调优。 BenchMark又叫做基准测试,…...
超完整的mysql安装配置方法(包含idea和navicat连接mysql,并实现建表)
mysql安装配置方法 1、下载mysql2、解压到指定的安装目录3、配置初始化文件my.ini4、配置用户变量和系统变量5、初始化mysql6、安装mysql服务并启动修改密码7、使用idea连接mysql8、使用Navicat可视化工具连接mysql,并实现新建数据库,新建表 1、下载mysq…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
