LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】
LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】
- 题目描述:
- 解题思路一:题意就是找出长度为m且连续重复k次的子数组。解题思路就是暴力枚举加剪枝。
- 解题思路二:思路差不多
- 解题思路三:0
题目描述:
给你一个正整数数组 arr,请你找出一个长度为 m 且在数组中至少重复 k 次的模式。
模式 是由一个或多个值组成的子数组(连续的子序列),连续 重复多次但 不重叠 。 模式由其长度和重复次数定义。
如果数组中存在至少重复 k 次且长度为 m 的模式,则返回 true ,否则返回 false 。
示例 1:
输入:arr = [1,2,4,4,4,4], m = 1, k = 3
输出:true
解释:模式 (4) 的长度为 1 ,且连续重复 4 次。注意,模式可以重复 k 次或更多次,但不能少于 k 次。
示例 2:
输入:arr = [1,2,1,2,1,1,1,3], m = 2, k = 2
输出:true
解释:模式 (1,2) 长度为 2 ,且连续重复 2 次。另一个符合题意的模式是 (2,1) ,同样重复 2 次。
示例 3:
输入:arr = [1,2,1,2,1,3], m = 2, k = 3
输出:false
解释:模式 (1,2) 长度为 2 ,但是只连续重复 2 次。不存在长度为 2 且至少重复 3 次的模式。
示例 4:
输入:arr = [1,2,3,1,2], m = 2, k = 2
输出:false
解释:模式 (1,2) 出现 2 次但并不连续,所以不能算作连续重复 2 次。
示例 5:
输入:arr = [2,2,2,2], m = 2, k = 3
输出:false
解释:长度为 2 的模式只有 (2,2) ,但是只连续重复 2 次。注意,不能计算重叠的重复次数。
提示:
2 <= arr.length <= 100
1 <= arr[i] <= 100
1 <= m <= 100
2 <= k <= 100
解题思路一:题意就是找出长度为m且连续重复k次的子数组。解题思路就是暴力枚举加剪枝。
class Solution:def containsPattern(self, arr: List[int], m: int, k: int) -> bool:def judge_same(i,j,m):for x,y in zip(range(i,i+m,1),range(j,j+m,1)):if arr[x] != arr[y]: return Falsereturn Truefor i in range(len(arr)-m):flag = 0for j in range(i+m,len(arr)-m+1,m):if j>(i+(k-1)*m): breakif judge_same(i,j,m): flag += 1continueif flag>=k-1: return True return False
时间复杂度:O(nmk)
空间复杂度:O(1)
解题思路二:思路差不多
class Solution:def containsPattern(self, arr: List[int], m: int, k: int) -> bool:n = len(arr)for l in range(n - m * k + 1):offset = 0while offset < m * k:if arr[l + offset] != arr[l + offset % m]:breakoffset += 1if offset == m * k:return Truereturn False
时间复杂度:O(nmk)
空间复杂度:O(1)
解题思路三:0
相关文章:

LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】
LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】 题目描述:解题思路一:题意就是找出长度为m且连续重复k次的子数组。解题思路就是暴力枚举加剪枝。解题思路二:思路差不多解题思路三:0 题目描述: 给你一个…...
QT5.4.1无法打开文件
问题描述:起初是在QT代码中运行打开文件代码: QString gFilename QFileDialog::getOpenFileName(this,"open File",path,"*", nullptr,QFileDialog::DontUseNativeDialog);时,出现了堵塞情况,经过多次实验一…...

【1day】金和OA某接口存在未授权访问漏洞
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...
使用Rust 构建C 组件
协议解析,这不就很快了,而且原生的标准库红黑树和avl 树支持,异步tokio 这些库,编写应用组件就很快了 rust 标准库不支持 unix 的消息队列,但是支持 shm 和 uds,后者从多方面考虑都比,消息队列更…...

AI:大模型技术
Prompt Prompt(提示)是一种在人工智能领域,特别是在自然语言处理和聊天机器人中常用的技术。它是一种输入,用于激发人工智能模型生成相应的输出。在聊天机器人中,用户输入的问题或请求就是提示,而聊天机器…...

揭开WPF里面XAML可以通过http引入命名空间的神秘面纱
前言 做WPF开发这么久,其实一直对头部引入命名空间有些疑问,为啥官方提供的库通过xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"引入,而我自己开发的就只能通过 xmlns:local="clr-namespace:Darren.Wpf.MainModule.Views"来引入…...

什么是高防IP,高防IP该如何选择。
高防IP,指的是高防御能力的IP地址。在互联网的世界里,网络安全问题成为一个重要的话题。作为一个用户,你是否曾遇到过被黑客攻击造成的网站瘫痪、信息泄露等问题?如果你是一个企业,你是否考虑过自己公司的网站和业务的…...

Linux 进程
文章目录 进程定义进程的描述查看进程方法进程状态进程优先级进程相关概念补充 进程定义 大多数的说法:进程是计算机中正在运行的程序的实例。它是操作系统对程序的一种抽象,用于管理和调度程序的执行。 个人理解: 从OS(操作系统)开始说起,…...
Docker部署开源分布式任务调度平台DolphinScheduler并实现远程访问办公
文章目录 前言1. 安装部署DolphinScheduler1.1 启动服务 2. 登录DolphinScheduler界面3. 安装内网穿透工具4. 配置Dolphin Scheduler公网地址5. 固定DolphinScheduler公网地址 前言 本篇教程和大家分享一下DolphinScheduler的安装部署及如何实现公网远程访问,结合内…...
SQL语言重温
数据库语言重温 笔记背景SQL教程一些最重要的 SQL 命令SQL WHERE 子句SQL AND & OR 运算符SQL ORDER BY 关键字 笔记背景 由于工作需要,现重温简单SQL语言,笔记记录如下。 SQL教程 SQL(Structured Query Language:结构化查询语言&…...

Java学习手册——第五篇数据类型
数据类型:是数据化的基石,如果没有数据类型怎么表示呢?比如年龄可以用整数:18岁。如果有更好的表示方式大家可以留言哟~ 在举个例子就是姓名,我们需要用字符串的形式来表示。这就是数据类型的魅力,而又有同…...
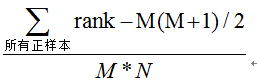
机器学习算法性能评估常用指标总结
考虑一个二分问题,即将实例分成正类(positive)或负类(negative)。对一个二分问题来说,会出现四种情况。如果一个实例是正类并且也被 预测成正类,即为真正类(True positive࿰…...

java面试题-ArrayList 和 LinkedList 的区别是什么
远离八股文,面试大白话,通俗且易懂 看完后试着用自己的话复述出来。有问题请指出,有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来,大家一起解决。 java面试题汇总-目录-持续更新中 ArrayLi…...

k8s中部署基于nfs的StorageClass
部署nfs服务 1.1 创建基础镜像(选做) 如果以docker的形式部署nfs server, 参考此步骤, 若否, 该步骤可忽略。 mkdir /data/nfs -p chmod 755 /data/nfs# NFS默认端口: 111、2049、20048 docker run -d \ --privileged \ --name nfs_server \ -p 111:111/tcp \ -p 111:111/ud…...

c语言一维数组总结详解
目录 介绍: 一维整型数组: 声明: 初始化: 打印输出: 输出结果: 浮点型数组: 代码: 运行结果: 补充: 一维字符数组: 字符数组声明及初始…...
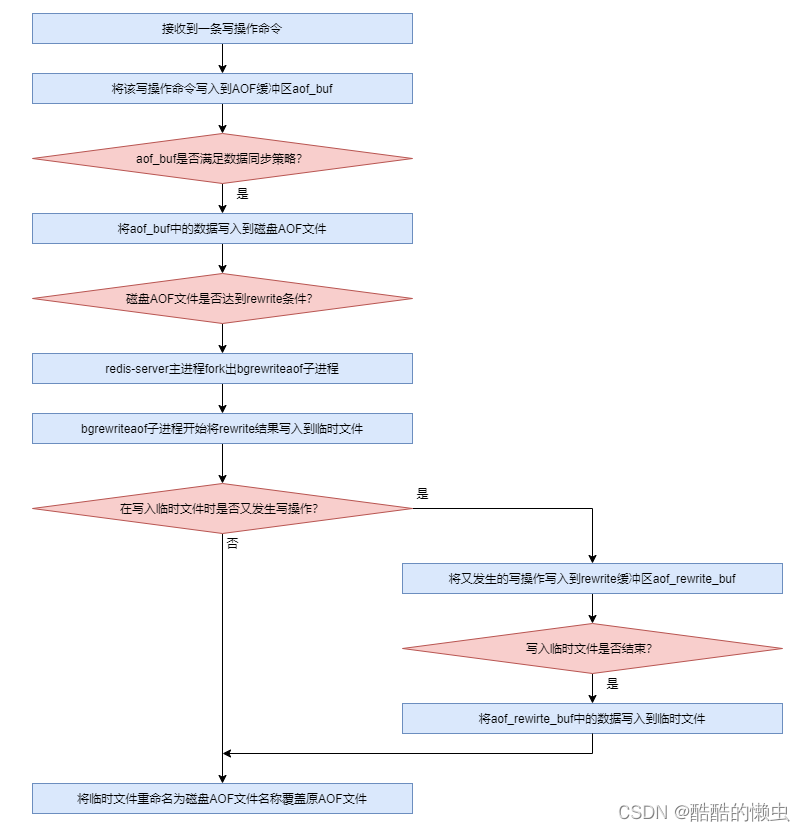
Redis 持久化 —— 超详细操作演示!
四、Redis 持久化 四、Redis 持久化4.1 持久化基本原理4.2 RDB持久化4.3 AOF持久化4.4 RDB与AOF对比4.5 持久化技术转型 五、Redis 主从集群六、Redis 分布式系统七、Redis 缓存八、Lua脚本详解九、分布式锁 数据库系列文章: 关系型数据库: MySQL —— 基础语法大全…...

使用Java实现桶排序算法
文章目录 桶排序算法 今天来看看桶排序算法: 桶排序算法 (1)基本思想:把数组 arr 划分为 n 个大小相同子区间(桶),每个子区间各自排序,最后合并 。计数排序是桶排序的一种特殊情况…...

5.题目:编号1624 小蓝吃糖果
题目: ### 这道题主要考察poriority_queue优先队列 #include<bits/stdc.h> using lllong long; using namespace std; int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n;cin>>n;priority_queue<int> pq;ll sum0,x;for(int i1;i<n;i){c…...

基于SpringBoot+thymeleaf协同过滤算法山河旅游推荐系统(Java毕业设计)
大家好,我是DeBug,很高兴你能来阅读!作为一名热爱编程的程序员,我希望通过这些教学笔记与大家分享我的编程经验和知识。在这里,我将会结合实际项目经验,分享编程技巧、最佳实践以及解决问题的方法。无论你是…...
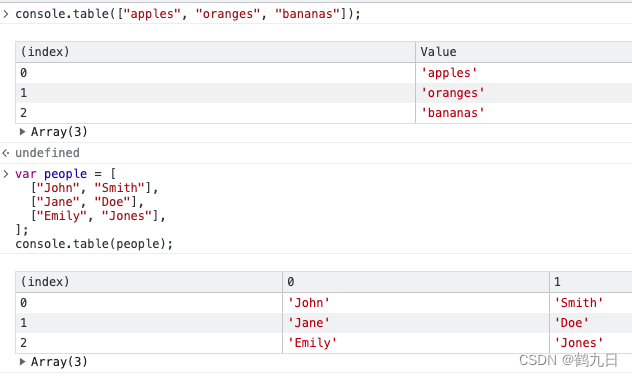
TypeScript 之 console的使用
语言: TypeScript 在线工具: PlayGround console console 对象是一个非常强大的控制台日志显示工具, 可以帮助我们在浏览器中调试代码。 注: console不属于TypeScript的语法,而是由JavaScript封装的内置对象。 简单的…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
