大话数据结构-查找-有序表查找
注:本文同步发布于稀土掘金。
3 有序表查找
3.1 折半查找
折半查找(Binary Search)技术,又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须采用顺序存储。
折半查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。不断重复上述过程,直到查找成功,或所有查找区域无记录,查找失败为止。
代码有多种实现方式,以下是示例:
/*** Binary Search** @author Korbin* @date 2023-04-19 17:57:03**/
public class BinarySearch<T extends Comparable<T>> {/*** binary search* <p>* return index in data if searched, else return -1** @param data array to search* @param key key to search* @return index of key in data* @author Korbin* @date 2023-04-19 18:30:33**/public int binarySearch(T[] data, T key) {int length = data.length;int from = 0;int to = length - 1;// if key little than data[0] or key greater than data[length - 1], return -1, means search failedif (data[from].compareTo(key) > 0 || data[to].compareTo(key) < 0) {return -1;}int mid = ((to - from) + 1) / 2;while (from < to) {// if data[mid] equals key, then return midif (data[mid].equals(key)) {return mid;}if (data[mid].compareTo(key) < 0) {// if key greater than data[mid], then search from [mid + 1, to]from = Math.min(mid + 1, length - 1);} else if (data[mid].compareTo(key) > 0) {// if key little than data[mid], then search from [from, mid - 1]to = Math.max(mid - 1, 0);}if (from == to) {// if from equals to, then check if data[from] equals keyreturn (data[from].equals(key)) ? from : -1;}mid = from + ((to - from) + 1) / 2;}return -1;}}
3.2 插值查找
插值查找(Interpolation Search)是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法,其核心在于插值公式 k e y − a [ f r o m ] a [ t o ] − a [ f l o w ] \frac {key-a[from]}{a[to]-a[flow]} a[to]−a[flow]key−a[from]。
从时间复杂度来看,它也是O(logn),但对于表长较大,而关键字又分布比较均匀的查找表来说,插值查找的平均性能要比折半查找算法的性能要好很多。反之,如果数组分布不均匀,用插值查找未必有优势。
插值查找是在折半查找的基础上进行优化的,在折半查找中,计算mid的算法为:
m i d = f r o m + 1 2 ( ( t o − f r o m ) + 1 ) mid = from + \frac {1}{2}((to - from) + 1) mid=from+21((to−from)+1)
在插值查找算法中,则是:
m i d = f r o m + k e y − a [ f r o m ] a [ t o ] − a [ f l o w ] ( ( t o − f r o m ) + 1 ) mid = from + \frac {key-a[from]}{a[to]-a[flow]}((to - from) + 1) mid=from+a[to]−a[flow]key−a[from]((to−from)+1)
因此代码只作少量改动:
/*** interpolation search* <p>* return index in data if searched, else return -1** @param data array to search* @param key key to search* @return index of key in data* @author Korbin* @date 2023-04-19 18:30:33**/
public int interpolationSearch(int[] data, int key) {int length = data.length;int from = 0;int to = length - 1;// if key little than data[0] or key greater than data[length - 1], return -1, means search failedif (data[from] > key || data[to] < key) {return -1;}int mid = ((key - data[from]) / (data[to] - data[from])) / 2 * ((to - from) + 1);while (from < to) {// if data[mid] equals key, then return midif (data[mid] == key) {return mid;}if (data[mid] < key) {// if key greater than data[mid], then search from [mid + 1, to]from = Math.min(mid + 1, length - 1);} else if (data[mid] > key) {// if key little than data[mid], then search from [from, mid - 1]to = Math.max(mid - 1, 0);}if (from == to) {// if from equals to, then check if data[from] equals keyreturn (data[from] == key) ? from : -1;}mid = from + ((key - data[from]) / (data[to] - data[from])) / 2 * ((to - from) + 1);}return -1;
}
调整一下mid的计算方式即可。
3.3 斐波那契查找
以下是一个斐波那契数组:
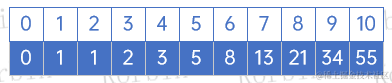
斐波那契数组的特性是,后一个元素的值等于前两个元素值的和,即F[K]=F[K-1]+F[K-2]。此外,F[K]/F[K+1]无限接近于0.618。斐波那契查找法依据这一特性,将数据分割成两部分,并把F[K-1]-1作为mid值进行对比处理。
例如,假设数组长度是8,8在斐波那契数组中的下标是6,那么把数组分为两段,长度分别是F[K-1]=F[5]=5,F[K-2]=F[4]=3,令mid=F[K-1]-1=5-1=4,比较要查找的数值与被查找的数组A中,下标为4的元素的大小。
在持续查找的过程中,被查找的数组A因为是有序数组,所以如果mid所对应的元素值大于要查找的数值时,进行下一轮查找时,则应到被查找数组的下半段去查找,下半段数组长度是多少呢?上文提到,裴波那契数组的特性F[K]=F[K-1]+F[K-2],而斐波那契查找就是将数组分成两段,前半段长度是F[K-2],后半段长度是F[K-1],因此当我们在后半段查找时,后半段的数组长度是F[K-1],即新的K=K-1,接下来的mid计算方式仍然不变。
而这种情况下,下标为mid以及其后的元素,在下一轮查找时显然不可以再用于查找,因此它们肯定会大于要查找的这个值,因此我们设置一个变量high,令其初始值为数组的长度,在A[mid]大于要查找的数值时,令high=mid-1,表示最多可以被查找的元素下标是high,对应的元素值是A[high]。
而如果mid所对应的元素值小于要查找的数值时,需要进行下一轮查找时,因为前半段长度为F[K-2],因此新的K=K-2,而mid的计算方式不再是mid=F[K-1]-1,而是“上一轮的mid”+1+F[K-1]-1,我们设置一个变更low,令其等于“上一轮的mid”+1,那么,mid的计算方式就变成了mid=low+F[K-1]-1,由于第一轮查找时没有“上一轮的mid”,所以如果按照这个公式,第一轮的low则为1,这样可以保证mid的计算公式一直是mid=low+F[K-1]-1。
根据以上分析,可知:
(1) 变量mid,表示使用数组中下标为mid的元素与要查找的数值进行比较;
(2) 变量k,表示被查找的数组长度在斐波那契数组中的位置;
(3) 变量low,表示从数组的下标为low的元素开始查找,初始值为1,当A[mid]<被查找的元素时,low=mid+1,同时置k=k-2;
(4) 变量high,表示最多查到数组的下标为high的元素,初始值为数组的最大下标,当A[mid]>被查找的元素时,high=mid-1,同时置k=k-1;
现在我们来开始尝试,假设有以下数组:

我们需要从中找到数值59所在的位置。
首先,初始化,low=1,high=数组的最大下标=10,同时定义一个斐波那契数组:
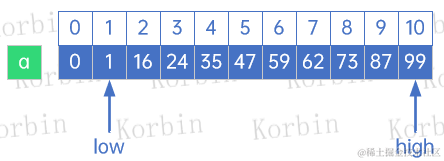

然后第一次查找,我们来找k,已知数组长度为11,在斐波那契数组f中并未找到10这个元素,有两个选择:

如果选择8,即k=6,f[k]=f[6]=8,假设我们要查找的是99,会出现什么情况呢:
(1) 第一轮,mid=low+f[k-1]-1=1+f[5]-1=1+5-1=5,由于a[mid]<要查找的数值,因此新的k=k-2=3,新的low=mid+1=5+1=6;
(2) 第二轮,mid=low+f[k-1]-1=6+f[2]-1=6+1-1=6,由于a[mid]<要查找的数值,因此,新的k=k-2=0,新的low=mid+1=6+1=7;
(3) 第三轮,mid=low+f[k-1]-1=7+f[0-1]-1,无法再继续,而此时仍有a[7]~a[10];
如果选择13,即k=7,f[k]=f[7]=13,假设我们要查找的是99,会出现什么情况呢:
(1) 第一轮,mid=low+f[k-1]-1=1+f[6]-1=1+8-1=8,a[8]<99,因此新的k=k-2=4,新的low=mid+1=8+1=9;
(2) 第二轮,mid=low+f[k-1]-1=9+f[3]-1=9+3-1=11,这时会发现,11已经超过了a的最大下标10,查找直接失败;
(3) 此时我们进行一些调整,将数组a的长度扩大到f[k]即13位,并补齐后两位的值为f[10],即f[11]=f[12]=f[10]=99,这时再来查询,就可以得到a[11]=99,找到99在数组a的下标为11的位置,而由于原始的a最大下标为10,因此直接返回10即可。
由此找到规则:当数组长度在斐波那契数组中找不到对应元素时,取与数组长度相邻,但大于数组长度的那个元素的下标作为k,同时将被查找的数组长度扩大到k,并补齐后续元素值使其等于被查找的数组的最后一个元素值。
因此我们取k=7,此时数组a和f的结构如下所示:
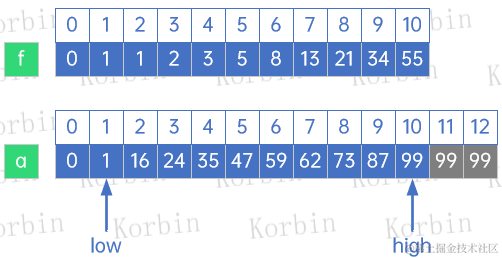
开始第一轮查找,此时mid=low+f[k-1]-1=1+f[6]-1=1+8-1=8,a[8]=73>59,因此high=mid-1=8-1=7,k=k-1=7-6=6:
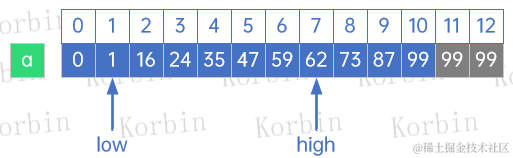
第二轮查找,mid=low+f[k-1]-1=1+f[5]-1=5,a[5]=47<59,因此low=mid+1=5+1=6,k=k-2=6-2=4:
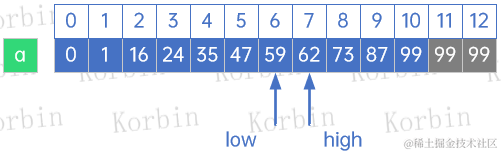
第三轮查找,mid=low+f[k-1]-1=6+f[2]-1=6+1-1=6,a[6]=59,得到查找结果,返回查找值59所在的下标是6,查找结束。
依据以上分析,代码实现比较简单:
import java.util.Arrays;/*** 斐波那契查找** @author Korbin* @date 2023-11-09 09:16:33**/
public class FibonacciSearch {/*** 定义一个斐波那契数组** @param length 数组长度* @return 斐波那契数组* @author Korbin* @date 2023-11-09 09:26:32**/private static int[] fibonacciArray(int length) {int[] array = new int[length];array[0] = 0;if (length == 1) {return array;} else if (length == 2) {array[1] = 1;return array;} else {array[1] = 1;for (int i = 2; i < length; i++) {array[i] = array[i - 1] + array[i - 2];}return array;}}/*** 查找key在数组array中的下标,找不到时返回-1** @param array 被查找的数组* @param key 要查找的key* @return key在array中的下标* @author Korbin* @date 2023-11-09 09:28:51**/private static int fibonacciSearch(int[] array, int key) {int length = array.length;// 如果被查找的数组只有一位,则直接比较返回if (length == 1) {if (array[0] == key) {return 0;} else {return -1;}}// 因为是从下标为1的数组开始查找的,因此先比较下标为0的元素if (array[0] == key) {return 0;}int[] fibonacciArray = fibonacciArray(length);// low初始为1int low = 1;// high初始为length - 1int high = length - 1;// 从斐波那契数组中找到kint k = 0;for (int i = 0; i < length; i++) {if (length > fibonacciArray[i]) {k++;}}// 如果被查找的数组长度小于k,则扩充数组int[] newArray = Arrays.copyOf(array, fibonacciArray[k]);if (fibonacciArray[k] > length) {for (int i = length; i < fibonacciArray[k]; i++) {newArray[i] = array[length - 1];}}// 开始查找while (low <= high) {// 计算midint mid = low + fibonacciArray[k - 1] - 1;if (key < newArray[mid]) {high = mid - 1;k = k - 1;} else if (key > newArray[mid]) {low = mid + 1;k = k - 2;} else {if (mid < length) {return mid;} else {return length - 1;}}}return -1;}public static void main(String[] args) {int[] array = new int[]{0, 1, 16, 24, 35, 47, 59, 62, 73, 87, 99};for (int j : array) {int index = fibonacciSearch(array, j);System.out.println("元素" + j + "的下标是" + index);}}}
相关文章:

大话数据结构-查找-有序表查找
注:本文同步发布于稀土掘金。 3 有序表查找 3.1 折半查找 折半查找(Binary Search)技术,又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须…...

Qt实现二维码生成和识别
一、简介 QZxing开源库: 生成和识别条码和二维码 下载地址:https://gitcode.com/mirrors/ftylitak/qzxing/tree/master 二、编译与使用 1.下载并解压,解压之后如图所示 2.编译 打开src目录下的QZXing.pro,选择合适的编译器进行编译 最后生…...
MyBatisX插件
MyBatisX插件 MyBatis-Plus为我们提供了强大的mapper和service模板,能够大大的提高开发效率。 但是在真正开发过程中,MyBatis-Plus并不能为我们解决所有问题,例如一些复杂的SQL,多表联查,我们就需要自己去编写代码和SQ…...

《C++20设计模式》学习笔记---原型模式
C20设计模式 第 4 章 原型模式4.1 对象构建4.2 普通拷贝4.3 通过拷贝构造函数进行拷贝4.4 “虚”构造函数4.5 序列化4.6 原型工厂4.7 总结4.8 代码 第 4 章 原型模式 考虑一下我们日常使用的东西,比如汽车或手机。它们并不是从零开始设计的,相反&#x…...

SpringBootAdmin设置邮件通知
如果你想要在Spring Boot Admin中配置邮件通知,可以按照以下步骤进行操作: 添加邮件通知的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId> </dep…...

深度解析IP应用场景API:提升风险控制与反欺诈能力
前言 在当今数字化时代,网络安全和用户数据保护成为企业日益关注的焦点。IP应用场景API作为一种强大的工具,不仅能够在线调用接口获取IP场景属性,而且具备识别IP真人度的能力,为企业提供了卓越的风险控制和反欺诈业务能力。本文将…...
Java连接数据库增删改查-MyBatis
准备工作: 1.创建一个springboot项目,并添加四个依赖 分别是,MyBatis的启动依赖和安装依赖,SQL的依赖,测试依赖,如下: 2.然后创建一张至少两条数据的表 (表可以用各种图形化工具创…...
在国内,现在月薪1万是什么水平?
看到网友发帖问:现在月薪1W是什么水平? 在现如今的情况下,似乎月薪过万这个标准已经成为衡量个人能力的一个标准了,尤其是现在互联网横行的时代,好像年入百万,年入千万就应该是属于大众的平均水平。 我不是…...

【Python网络爬虫入门教程1】成为“Spider Man”的第一课:HTML、Request库、Beautiful Soup库
Python 网络爬虫入门:Spider man的第一课 写在最前面背景知识介绍蛛丝发射器——Request库智能眼镜——Beautiful Soup库 第一课总结 写在最前面 有位粉丝希望学习网络爬虫的实战技巧,想尝试搭建自己的爬虫环境,从网上抓取数据。 前面有写一…...
燕千云汇联易联袂出击:护航医企合规,丝滑内外协作
👉 如想详细了解燕千云医药行业快速实施包(ITFA),可继续阅读详细内容: 文/玉娇龙 一. 医药行业数字化挑战 医药研发从基础研究到最终注册上市的整个生命周期长则需要10多年,短则需要6-7年,在漫长…...

【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵 2023年11月3日 #algebra 文章目录 Jordan型矩阵1. 代数重数与几何重数2. Jordan块与Jordan标准型2.1 最小多项式与Jordan标准型2.2 两类重要矩阵 3. 矩阵的Jordan分解3.1 Jordan分解的应用 下链 1. 代数重数与几何重数 在对向量做线性变换时,向量空间…...

laravel的ORM 对象关系映射
Laravel 中的 ORM(Eloquent ORM)是 Laravel 框架内置的一种对象关系映射系统,用于在 PHP 应用中与数据库进行交互。Eloquent 提供了一种优雅而直观的语法,使得开发者可以使用面向对象的方式进行数据库查询和操作。 定义模型&…...

049:VUE 引入jquery的方法和配置
第049个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...
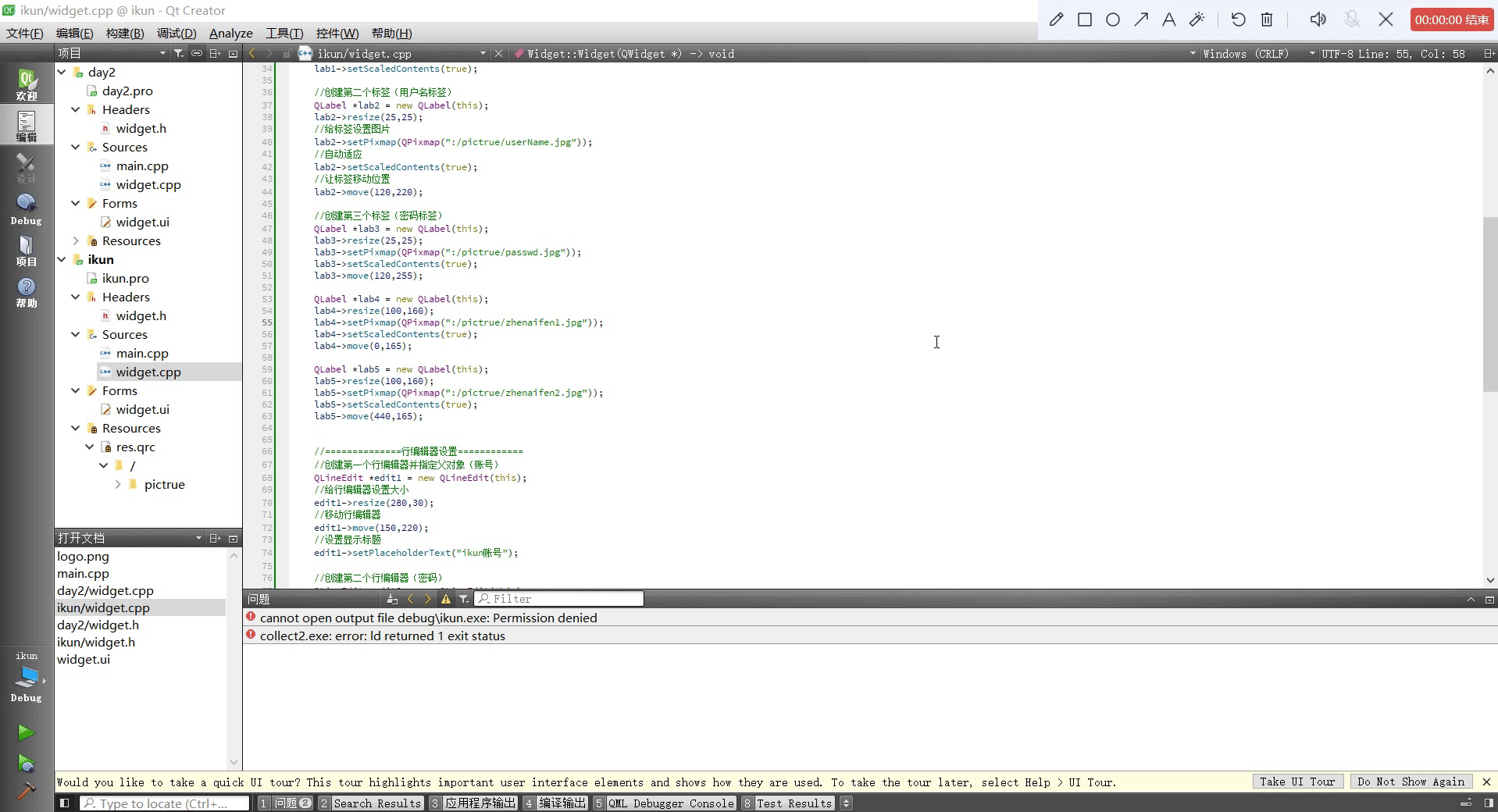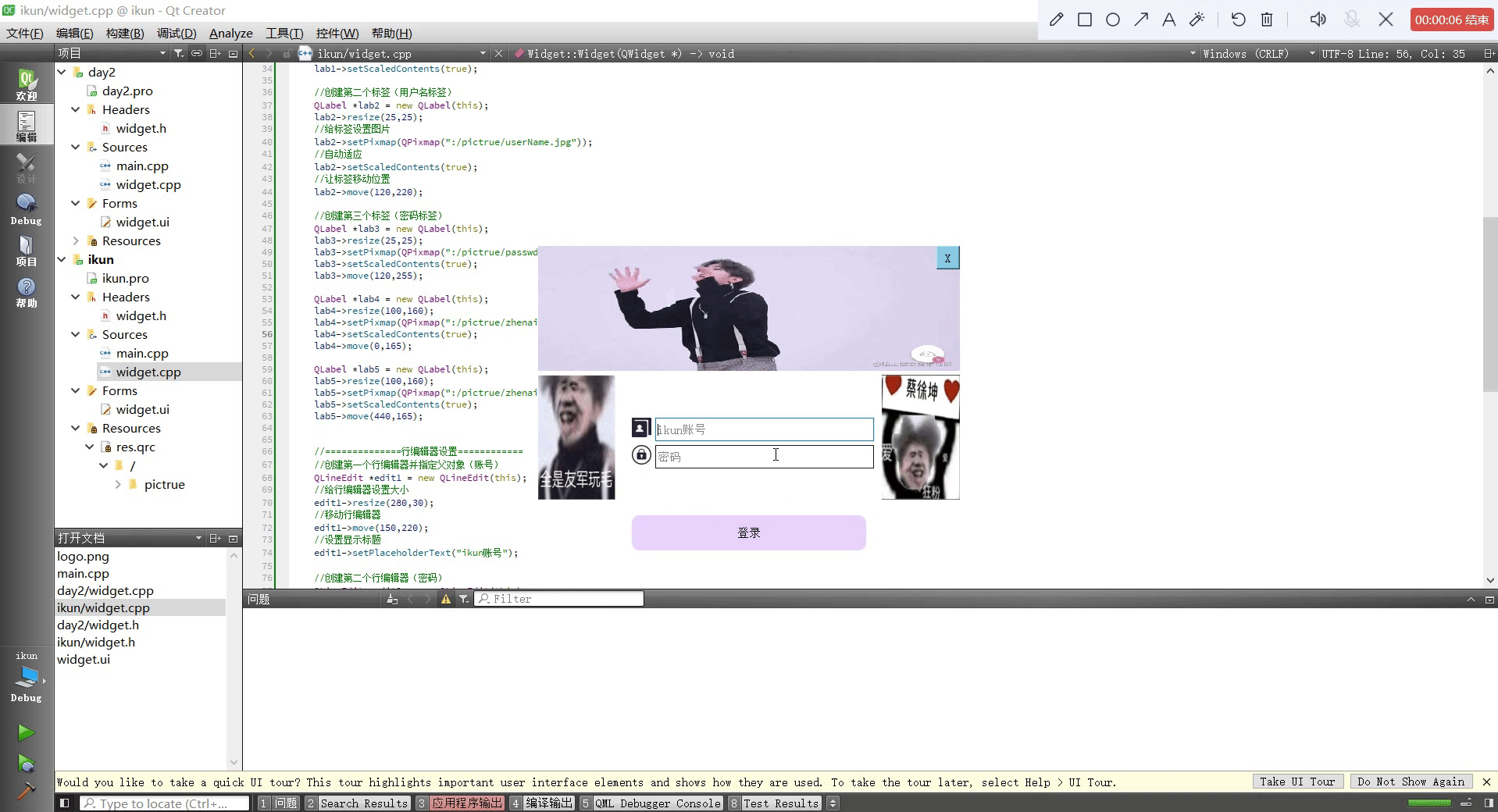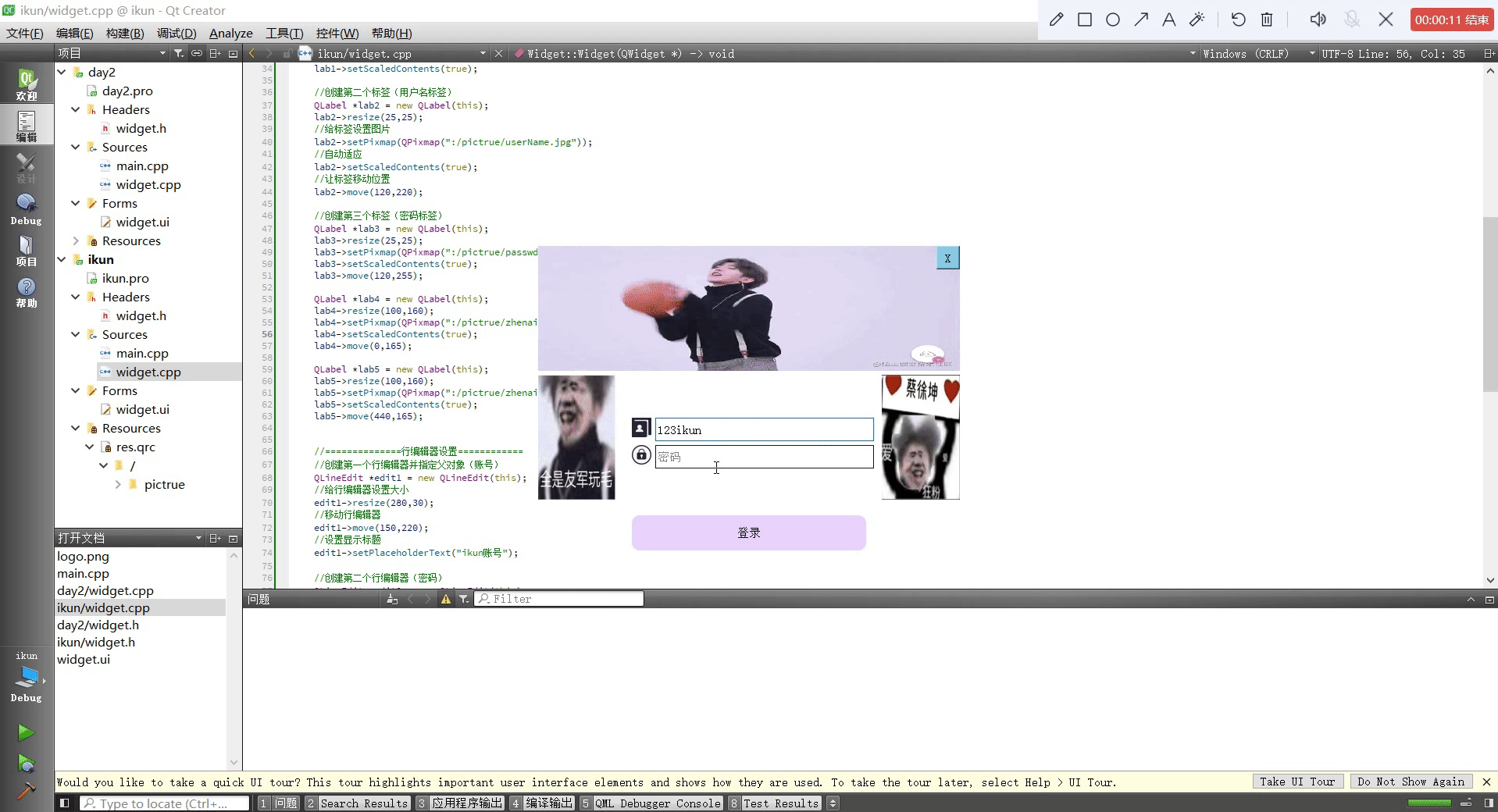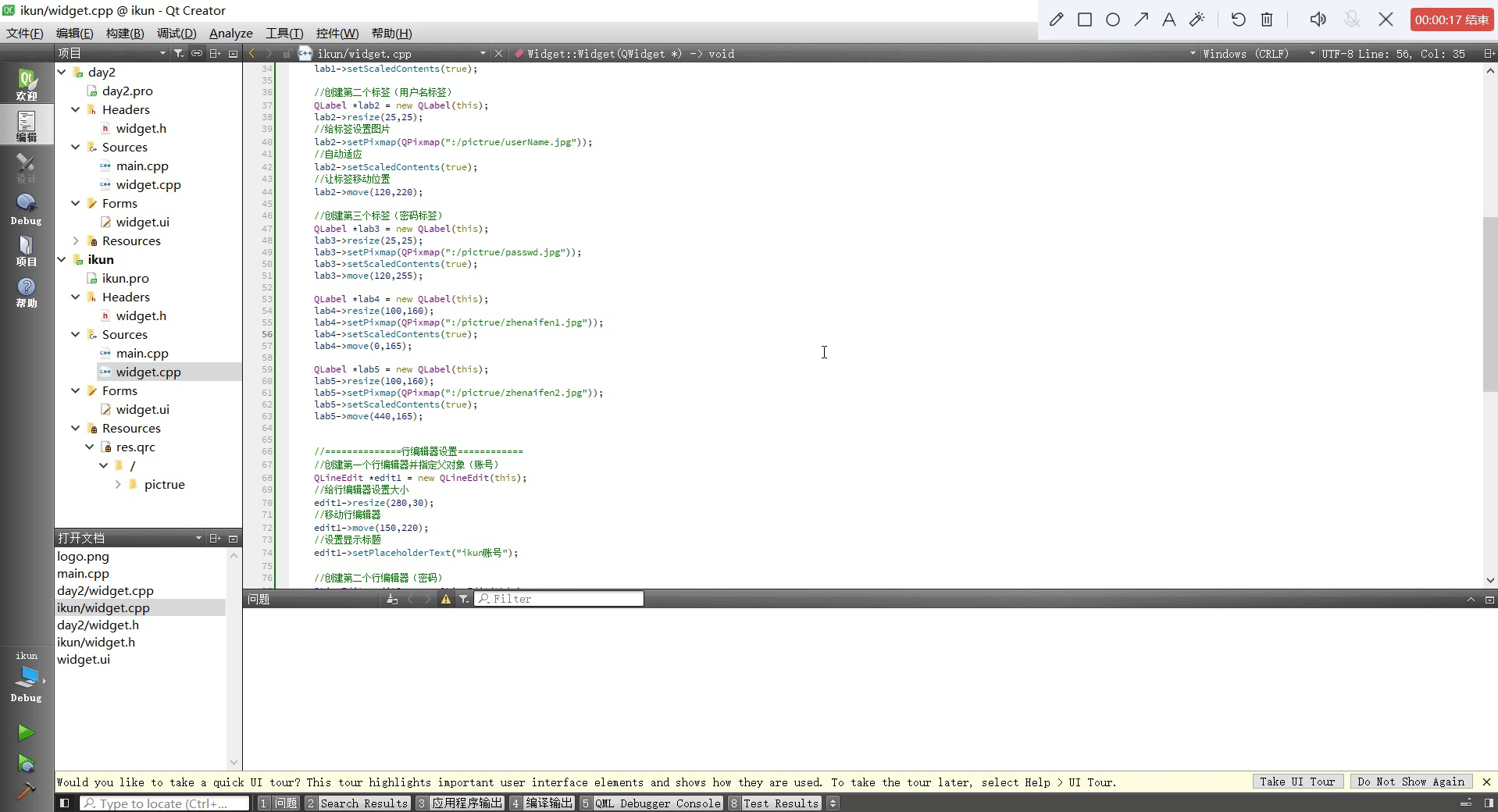
Qt设置类似于qq登录页面
头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QWindow> #include <QIcon> #include <QLabel> #include <QMovie> #include <QLineEdit> #include <QPushButton>QT_BEGIN_NAMESPACE namespace Ui { class…...
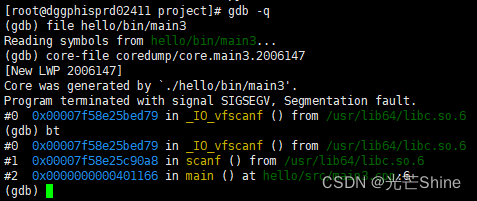
【GDB】
GDB 1. GDB调试器1.1 前言1.2 GDB编译程序1.3 启动GDB1.4 载入被调试程序1.5 查看源码1.6 运行程序1.7 断点设置1.7.1 通过行号设置断点1.7.2 通过函数名设置断点1.7.3 通过条件设置断点1.7.4 查看断点信息1.7.5 删除断点 1.8 单步调试1.9 2. GDB调试core文件2.1 设定core文件的…...

深入了解Java Duration类,对时间的精细操作
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概6000多字,预计阅读时间长需要5分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...

Python:核心知识点整理大全5-笔记
目录 2. 使用方法pop()删除元素 3. 弹出列表中任何位置处的元素 4. 根据值删除元素 3 章 列表简介 3.3 组织列表 3.3.1 使用方法 sort()对列表进行永久性排序 3.3.2 使用函数 sorted()对列表进行临时排序 3.3.3 倒着打印列表 3.3.4 确定列表的长度 3.5 小结 2. 使用方…...
、微调(fine-tuning)、迁移学习(transfer learning))
预训练(pre-learning)、微调(fine-tuning)、迁移学习(transfer learning)
预训练(pre-learning) 搭建一个网络模型来完成一个特定的图像分类的任务。首先,你需要随机初始化参数,然后开始训练网络,不断调整参数,直到网络的损失越来越小。在训练的过程中,一开始初始化的…...

王道数据结构课后代码题 p149 第8—— 12(c语言代码实现)
目录 8.假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。 9.设树B是一棵采用链式结构存储的二叉树,编写一个把树 B中所有结点的左、右子树进行交换的函数。 10.假设二叉树采用二叉链存储结构存储…...
Nginx服务优化以及防盗链
1. 隐藏版本号 以在 CentOS 中使用命令 curl -I http://192.168.66.10 显示响应报文首部信息。 查看版本号 curl -I http://192.168.66.10 1. 修改配置文件 vim /usr/local/nginx/conf/nginx.conf http {include mime.types;default_type application/octet-stream;…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
