【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵
2023年11月3日
#algebra
文章目录
- Jordan型矩阵
- 1. 代数重数与几何重数
- 2. Jordan块与Jordan标准型
- 2.1 最小多项式与Jordan标准型
- 2.2 两类重要矩阵
- 3. 矩阵的Jordan分解
- 3.1 Jordan分解的应用
- 下链
1. 代数重数与几何重数
在对向量做线性变换时,向量空间的某个向量的方向不发生改变,而只是在其方向上进行拉伸,则该向量是线性变换的特征向量,其在变换中被拉伸的倍数为该特征向量的特征值(特征根)。
矩阵的相同特征值有其对应的代数重数与几何重数,相同特征值的代数重数就是相同特征值的个数,几何重数就是相同特征值所对应特征向量的个数。显然,特征向量的拉伸量可能相同,即代数重数大于等于几何重数,也就是多个相同特征值可能对应一个特征向量。也可以说,对同一个特征值,可能有多个特征向量,而该特征值的代数重数大于等于特征向量的个数。
如果每个相同的特征值都对应不同的特征向量,则代数重数等于几何重数。
对于 n × n n\times n n×n 矩阵 A A A,有 l l l 个特征根, l < n l\lt n l<n 且第 i i i 个特征根 λ i \lambda_i λi 的代数重数为 σ i \sigma_i σi 、几何重数为 α i \alpha_i αi
det ( λ I n − A ) = ( λ − λ 1 ) σ 1 ( λ − λ 2 ) σ 2 ⋯ ( λ − λ l ) σ l \det (\lambda I_n-A)=(\lambda-\lambda_1)^{\sigma_1}(\lambda-\lambda_2)^{\sigma_2}\cdots(\lambda-\lambda_l)^{\sigma_l} det(λIn−A)=(λ−λ1)σ1(λ−λ2)σ2⋯(λ−λl)σl
第 i i i个特征根的几何重数计算如下:
α i = n − rank ( λ i I n − A ) \alpha_i=n-\text{rank}(\lambda_iI_n-A) αi=n−rank(λiIn−A)
几何重数(零化度)对应着有几个线性无关的特征向量拥有当前的特征值。
在Jordan标准型中,几何重数对应着当前特征值拥有几个Jordan快。
若代数重数等于几何重数,该特征值为 半单的。
若代数重数大于几何重数,该特征值为 亏损的。
显然,代数重数为 1 {1} 1 的特征值一定时半单的;不同特征值对应的特征向量是线性无关的。每个特征值都是半单的矩阵(有完备的特征向量系)等价于可对角化。
存在亏损的特征值的矩阵称为亏损矩阵,等价于不可对角化。
2. Jordan块与Jordan标准型
举例,对代数重数为 σ i = 5 \sigma_i=5 σi=5 、几何重数为 α i = 2 \alpha_i=2 αi=2 的特征根 λ i \lambda_i λi,有两个Jordan快,设存在一个三阶和一个两阶的Jordan块:
J i = [ λ i 1 0 0 0 0 λ i 1 0 0 0 0 λ i 0 0 0 0 0 λ i 1 0 0 0 0 λ i ] = diag ( J 3 ( λ i ) , J 2 ( λ i ) ) J_{i}= \begin{bmatrix} \lambda_i&1&0&0&0\\ 0&\lambda_i&1&0&0\\ 0&0&\lambda_i&0&0\\ 0&0&0&\lambda_i&1\\ 0&0&0&0&\lambda_i \end{bmatrix}=\text{diag}(J_3(\lambda_i),J_2(\lambda_i)) Ji= λi00001λi00001λi00000λi00001λi =diag(J3(λi),J2(λi))
Jordan块的顺序可以交换。知道特征值的代数重数和几何重数,还需要知道特征值对应的每阶Jordan块的个数,才能写出Jordan标准型。
可以通过幂零矩阵确定 λ i \lambda_i λi 对应的两个Jordan快各有几阶,如其中 j j j 阶Jordan块的个数为:
r j + 1 + r j − 1 − 2 r j r_{j+1}+r_{j-1}-2r_j rj+1+rj−1−2rj
r j = rank ( λ i I − A ) j r_j=\text{rank}(\lambda_iI-A)^j rj=rank(λiI−A)j
r 0 = rank ( λ i I − A ) 0 = n r_0=\text{rank}(\lambda_iI-A)^0=n r0=rank(λiI−A)0=n
矩阵的Jordan标准型
J = diag ( J n 1 , J n 2 , ⋯ , J n k ) , n 1 + n 2 + ⋯ + n k = n J=\text{diag}(J_{n_1},J_{n_2},\cdots,J_{n_k}),~n_1+n_2+\cdots+n_k=n J=diag(Jn1,Jn2,⋯,Jnk), n1+n2+⋯+nk=n
Jordan块的上次对角元值都为 1 {1} 1
J n i = [ λ i 1 λ i 1 ⋱ ⋱ λ i 1 λ i ] J_{n_i}= \begin{bmatrix} \lambda_i&1&&&\\ &\lambda_i&1&&\\ &&\ddots&\ddots&\\ &&&\lambda_i&1\\&&&&\lambda_i \end{bmatrix} Jni= λi1λi1⋱⋱λi1λi
在这种定义下,不同Jordan块可能对应相同特征值。求Jordan标准型步骤如下:
- 算特征值
- 算代数重数、几何重数
- 算特征值对应阶数Jordan块的个数
[!example]-
求矩阵 A A A 的Jordan标准型
A = [ 2 0 − 1 0 − 1 1 0 − 1 0 0 2 0 1 1 1 3 ] A= \begin{bmatrix} 2 & 0 & -1 & 0 \\ -1 & 1 & 0 & -1 \\ 0 & 0 & 2 & 0\\ 1 & 1 & 1 & 3 \end{bmatrix} A= 2−1010101−10210−103
解:
det ( λ I − A ) = ( λ − 2 ) 4 \det ( \lambda I-A)=( \lambda-2)^4 det(λI−A)=(λ−2)4
λ 1 = λ 2 = λ 3 = λ 4 = 2 , 4 − rank ( λ 1 I − A ) = 2 \lambda_1= \lambda_2 = \lambda_3= \lambda_4=2 \,\,,\,\, 4- \text{rank} ( \lambda_1I-A)=2 λ1=λ2=λ3=λ4=2,4−rank(λ1I−A)=2
2 2 2 特征值的代数重数是 4 {4} 4 ,几何重数是 2 {2} 2 ,有两个Jordan块,可能是一个三阶和一个一阶的,也可能是两个二阶的。
r 0 = 4 r 1 = rank ( λ 1 I − A ) = 2 r 2 = rank ( λ 1 I − A ) 2 = 0 r 3 = rank ( λ 1 I − A ) 3 = 0 \begin{align*} r_0=&4 \\ \\ r_1=& \text{rank}( \lambda_1I-A)=2 \\ \\ r_2=& \text{rank} ( \lambda_1I-A)^2=0 \\ \\ r_3=& \text{rank} ( \lambda_1I-A)^3=0 \\ \\ \end{align*} r0=r1=r2=r3=4rank(λ1I−A)=2rank(λ1I−A)2=0rank(λ1I−A)3=0
2 2 2 特征值对应的一阶Jordan块个数
r 2 + r 0 − 2 r 1 = 0 r_2+r_0-2r_1=0 r2+r0−2r1=0
2 2 2 特征值对应的二阶Jordan块个数
r 3 + r 1 − 2 r 2 = 2 r_3+r_1-2r_2=2 r3+r1−2r2=2
所以有两个二阶Jordan块,Jordan标准型为
J = [ 2 1 0 0 0 2 0 0 0 0 2 1 0 0 0 2 ] J= \begin{bmatrix} 2 & 1 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 1\\ 0 & 0 & 0 & 2 \end{bmatrix} J= 2000120000200012
Jordan块减去特征值单位阵拥有幂零的特性:
( J n i − λ i I n i ) n i = 0 (J_{n_i}- \lambda_iI_{n_i})^{n_i}=0 (Jni−λiIni)ni=0
2.1 最小多项式与Jordan标准型
由于一个特征值可能对应多个Jordan块,我们选择一个特征值的最大Jordan块的阶数,做为最小多项式中该特征值对应因子的幂次,得到最小多项式。例如
A = [ λ 1 1 0 0 0 0 λ 1 1 0 0 0 0 λ 1 0 0 0 0 0 λ 1 0 0 0 0 0 λ 2 ] A= \begin{bmatrix} \lambda_1 & 1 & 0 & 0&0 \\ 0 & \lambda_1 & 1 & 0&0 \\ 0 &0 & \lambda_1 & 0&0\\ 0 & 0& 0 & \lambda_1&0\\0 & 0& 0& 0& \lambda2 \end{bmatrix} A= λ100001λ100001λ100000λ100000λ2
特征多项式为
Δ ( λ ) = det ( λ I − A ) = ( λ − λ 1 ) 4 ( λ − λ 2 ) \Delta( \lambda)=\det( \lambda I-A)=( \lambda- \lambda_1)^4( \lambda- \lambda_2) Δ(λ)=det(λI−A)=(λ−λ1)4(λ−λ2)
最小多项式为
ψ ( λ ) = ( λ − λ 1 ) 3 ( λ − λ 2 ) \psi( \lambda)=( \lambda- \lambda_1)^3( \lambda- \lambda_2) ψ(λ)=(λ−λ1)3(λ−λ2)
所有相似矩阵都有相同的最小多项式。
2.2 两类重要矩阵
一类是每个特征值代数重数与几何重数相等的矩阵,又称非退化矩阵或简单矩阵、可对角化矩阵,其Jordan标准型是对角阵。
另一类是每个特征值的几何重数都为 1 {1} 1 的矩阵,也就是一个特征值对应一个Jordan块,各Jordan块对应的特征值互异,又称循环矩阵。
显然,循环矩阵的特征多项式与最小多项式相同。
3. 矩阵的Jordan分解
对 n {n} n 阶方阵 A A A,存在 n {n} n 阶可逆矩阵 T T T,使得
A = T J T − 1 A=TJT^{-1} A=TJT−1
为矩阵Jordan分解, J J J 为矩阵的Jordan标准型,若不计Jordan块的次序,则Jordan标准型唯一。
对变换矩阵,可以写为矩阵的集合 T = ( T 1 , T 2 , ⋯ , T k ) T=(T_1,T_2,\cdots,T_k) T=(T1,T2,⋯,Tk), T i T_i Ti 为 n × n i n\times n_i n×ni 阶矩阵。
A ( T 1 , T 2 , ⋯ , T k ) = ( T 1 , T 2 , ⋯ , T k ) [ J n 1 ⋱ J n k ] A(T_1,T_2,\cdots,T_k)=(T_1,T_2,\cdots,T_k) \begin{bmatrix}J_{n_1}&&\\&\ddots\\&&J_{n_k}\end{bmatrix} A(T1,T2,⋯,Tk)=(T1,T2,⋯,Tk) Jn1⋱Jnk
A T i = T i J n i = ( t 1 i , t 2 i , ⋯ , t n i i ) [ λ i 1 λ i 1 ⋱ ⋱ λ i 1 λ i ] AT_i=T_iJ_{n_i}=(t_1^i,t_2^i,\cdots,t_{n_i}^i) \begin{bmatrix} \lambda_i&1&&&\\ &\lambda_i&1&&\\ &&\ddots&\ddots&\\ &&&\lambda_i&1\\&&&&\lambda_i \end{bmatrix} ATi=TiJni=(t1i,t2i,⋯,tnii) λi1λi1⋱⋱λi1λi
所以
{ A t 1 i = λ i t 1 i A t 2 i = λ i t 2 i + t 1 i ⋮ A t n i i = λ i t n i i + t n i − 1 i \begin{cases} At_1^i=\lambda_it_1^i \\ At_2^i=\lambda_it_2^i+t_1^i\\ \vdots\\ At_{n_i}^i=\lambda_it_{n_i}^i+t_{n_i-1}^i \end{cases} ⎩ ⎨ ⎧At1i=λit1iAt2i=λit2i+t1i⋮Atnii=λitnii+tni−1i
( A − λ i I n ) t 1 i = 0 (A-\lambda_iI_n)t_1^i=0 (A−λiIn)t1i=0
( A − λ i I n ) t j i = t j − 1 i , j = 2 , 3 ⋯ , n i (A-\lambda_iI_n)t_j^i=t_{j-1}^i,~j=2,3\cdots,n_i (A−λiIn)tji=tj−1i, j=2,3⋯,ni
t 1 i , t 2 i , ⋯ , t n i i t_1^i,t_2^i,\cdots,t_{n_i}^i t1i,t2i,⋯,tnii 构成一条关于 λ i \lambda_i λi的长度为 n i n_i ni的Jordan链。 t 1 i t_1^i t1i 是链首,是 A A A 关于 λ i \lambda_i λi 的一个特征向量。
链首满足是特征向量,且方程组可解的要求。所以把 λ i \lambda_i λi 对应的所有线性无关的特征向量算出来,做线性组合,作为链首。变换矩阵 T T T 的求解步骤如下
- 求Jordan标准型
- 算每个Jordan块对应的Jordan链
若Jordan块阶数为1,直接计算特征向量
若阶数大于1,先计算特征向量,利用特征向量的线性组合得到链首(同一特征值特征向量非零线性组合仍是特征向量)
[!example]-
A A A 的Jordan标准型
A = [ 3 0 8 3 − 1 6 − 2 0 − 5 ] , J = [ − 1 0 0 0 − 1 1 0 0 − 1 ] A= \begin{bmatrix} 3 & 0 & 8 \\ 3 & -1 & 6 \\ -2 & 0 & -5 \end{bmatrix} \,\,,\,\, J= \begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & -1 \end{bmatrix} A= 33−20−1086−5 ,J= −1000−1001−1
求出 λ 1 \lambda_1 λ1 对应的线性无关的特征向量
x 1 = ( 2 , 0 , − 1 ) T , x 2 = ( 0 , 1 , 0 ) T x_1=(2,0,-1)^ \mathrm T \,\,,\,\, x_2=(0,1,0)^ \mathrm T x1=(2,0,−1)T,x2=(0,1,0)T
对应的变换矩阵为 x 1 x_1 x1 和 x 2 x_2 x2 的线性组合,我们选取 x 1 x_1 x1。对于阶数为 2 {2} 2 的Jordan块,构造 y = k 1 x 1 + k 2 x 2 y=k_1x_1+k_2x_2 y=k1x1+k2x2 使得 ( A − λ 1 I ) Z = y (A- \lambda_1I)Z=y (A−λ1I)Z=y 可解,即
rank ( A − λ 1 I ) = rank ( A − λ 1 I ∣ y ) \text{rank}(A- \lambda_1I)= \text{rank}(A- \lambda_1I\,|\,y) rank(A−λ1I)=rank(A−λ1I∣y)
( A − λ 1 I ∣ y ) = [ 4 0 8 2 k 1 3 0 6 k 2 − 2 0 − 4 − k 1 ] → [ 4 0 8 2 k 1 0 0 0 k 2 − 3 k 1 / 2 0 0 0 0 ] (A- \lambda_1I\,|\,y) = \begin{bmatrix} 4 & 0 & 8 & 2k_1 \\ 3 & 0 & 6& k_2 \\ -2 & 0 & -4 &-k_1 \end{bmatrix} \to \begin{bmatrix} 4 & 0 & 8 & 2k_1 \\ 0 & 0 & 0& k_2-3k_1/2 \\ 0 & 0 &0 &0 \end{bmatrix} (A−λ1I∣y)= 43−200086−42k1k2−k1 → 4000008002k1k2−3k1/20
需要 2 k 2 − 3 k 1 = 0 2k_2-3k_1=0 2k2−3k1=0 ,取 k 1 = 2 , k 2 = 3 , y = ( 4 , 3 , − 2 ) T k_1=2 \,\,,\,\, k_2=3 \,\,,\,\, y=(4,3,-2)^ \mathrm T k1=2,k2=3,y=(4,3,−2)T, 解出 z = ( 1 , 0 , 0 ) T z=(1,0,0)^ \mathrm T z=(1,0,0)T,鼓变换矩阵为
T = [ 2 4 1 0 3 0 − 1 − 2 0 ] T= \begin{bmatrix} 2 & 4 & 1 \\ 0 & 3 & 0 \\ -1 & -2 & 0 \end{bmatrix} T= 20−143−2100
3.1 Jordan分解的应用
Jordan分解用于计算初等函数在某个矩阵处的值,最简单的情形是计算多项式函数(高次多项式),当然也可以用Cayley-Hamilton定理。
[!example]-
设矩阵
A = [ − 1 0 1 1 2 0 − 4 0 3 ] A= \begin{bmatrix} -1 & 0 & 1 \\ 1 & 2 & 0 \\ -4 & 0 & 3 \end{bmatrix} A= −11−4020103
求 A 2018 A^{2018} A2018。
解:
T − 1 A T = J = [ 1 1 0 0 1 0 0 0 2 ] → A 2018 = T J 2018 T − 1 \begin{align*} T^{-1}AT=J= \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \end{align*}\to A^{2018}=TJ^{2018}T^{-1} T−1AT=J= 100110002 →A2018=TJ2018T−1
A 2018 = [ 1 0 0 − 1 − 1 1 2 1 0 ] [ 1 2018 0 0 1 0 0 0 2 2018 ] [ 1 0 0 − 2 0 1 − 1 1 1 ] = [ − 4035 0 2018 4037 − 2 2018 2 2018 2 2018 − 2019 − 8072 0 4037 ] \begin{align*} A^{2018}=& \begin{bmatrix} 1 & 0 & 0 \\ -1 & -1 & 1 \\ 2 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2018 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2^{2018} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ -2 & 0 & 1 \\ -1 & 1 & 1 \end{bmatrix} \\ \\=& \begin{bmatrix} -4035 & 0 & 2018 \\ 4037-2^{2018} & 2^{2018} & 2^{2018}-2019 \\ -8072 & 0 & 4037 \end{bmatrix} \end{align*} A2018== 1−120−11010 1002018100022018 1−2−1001011 −40354037−22018−80720220180201822018−20194037
Jordan分解还可以用于求解一阶线性常系数微分方程组。
[! example]-
求解
{ d d t x 1 = 3 x 1 + x 2 − 3 d d t x 2 = − 2 x 2 + 2 x 3 d d t x 3 = − x 1 + x 2 + 3 x 3 \begin{cases} \frac{\mathrm d }{\mathrm dt}x_1=3x_1+x_2-3 \\ \frac{\mathrm d }{\mathrm dt}x_2=-2x_2+2x_3\\ \frac{\mathrm d }{\mathrm dt}x_3=-x_1+x_2+3x_3 \end{cases} ⎩ ⎨ ⎧dtdx1=3x1+x2−3dtdx2=−2x2+2x3dtdx3=−x1+x2+3x3
解:令 x = ( x 1 , x 2 , x 3 ) T x=(x_1,x_2,x_3)^ \mathrm T x=(x1,x2,x3)T ,则原方程组化为
d x d t = A x \frac{\mathrm d x}{\mathrm dt}=Ax dtdx=Ax
令 x = T y x=Ty x=Ty,则
d y d t = T − 1 d x d t = T − 1 A x = T − 1 A T y = J y \frac{\mathrm d y}{\mathrm dt}= T^{-1}\frac{\mathrm d x}{\mathrm dt}=T^{-1}Ax=T^{-1}ATy=Jy dtdy=T−1dtdx=T−1Ax=T−1ATy=Jy
A = [ 3 1 − 1 − 2 0 2 − 1 − 1 3 ] , J = [ 2 0 0 0 2 1 0 0 2 ] A= \begin{bmatrix} 3 & 1 & -1 \\ -2 & 0 & 2 \\ -1 & -1 & 3 \end{bmatrix} \,\,,\,\, J= \begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{bmatrix} A= 3−2−110−1−123 ,J= 200020012
∴ J y = [ 2 y 1 2 y 2 + y 3 2 y 3 ] → y 1 ′ = 2 y 1 , y 2 ′ = 2 y 2 + y 3 , y 3 ′ = 2 y 3 \therefore Jy= \begin{bmatrix} 2y_1\\ 2y_2+y_3\\ 2y_3 \end{bmatrix}\to y_1'=2y_1 \,\,,\,\, y_2'=2y_2+y_3 \,\,,\,\, y_3'=2y_3 ∴Jy= 2y12y2+y32y3 →y1′=2y1,y2′=2y2+y3,y3′=2y3
y y y 第一第三个分量的一般解为
y 1 ( t ) = c 1 e 2 t , y 3 ( t ) = c 3 e 2 t y_1(t)=c_1e^{2t} \,\,,\,\, y_3(t)=c_3e^{2t} y1(t)=c1e2t,y3(t)=c3e2t
代入第二个分量求解得
y 2 ( t ) = ( c 2 + c 3 t ) e 2 t y_2(t)=(c_2+c_3t)e^{2t} y2(t)=(c2+c3t)e2t
x = T y = [ − e 2 t ( c 1 + c 2 + c 3 + c 3 t ) e 2 t ( c 1 + 2 c 2 + 2 c 3 t ) e 2 t ( c 2 + c 3 t ) ] , ∀ c 1 , c 2 , c 3 ∈ C x=Ty= \begin{bmatrix} -e^{2t}(c_1+c_2+c_3+c_3t)\\ e^{2t}(c_1+2c_2+2c_3t)\\ e^{2t}(c_2+c_3t) \end{bmatrix} \,\,,\,\, \forall c_1,c_2,c_3\in \mathbb C x=Ty= −e2t(c1+c2+c3+c3t)e2t(c1+2c2+2c3t)e2t(c2+c3t) ,∀c1,c2,c3∈C
下链
Jordan块、Jordan标准型及矩阵的Jordan分解
矩阵论 武汉理工大学 (亲测最好的矩阵论视频)
相关文章:

【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵 2023年11月3日 #algebra 文章目录 Jordan型矩阵1. 代数重数与几何重数2. Jordan块与Jordan标准型2.1 最小多项式与Jordan标准型2.2 两类重要矩阵 3. 矩阵的Jordan分解3.1 Jordan分解的应用 下链 1. 代数重数与几何重数 在对向量做线性变换时,向量空间…...

laravel的ORM 对象关系映射
Laravel 中的 ORM(Eloquent ORM)是 Laravel 框架内置的一种对象关系映射系统,用于在 PHP 应用中与数据库进行交互。Eloquent 提供了一种优雅而直观的语法,使得开发者可以使用面向对象的方式进行数据库查询和操作。 定义模型&…...

049:VUE 引入jquery的方法和配置
第049个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...
Qt设置类似于qq登录页面
头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QWindow> #include <QIcon> #include <QLabel> #include <QMovie> #include <QLineEdit> #include <QPushButton>QT_BEGIN_NAMESPACE namespace Ui { class…...
【GDB】
GDB 1. GDB调试器1.1 前言1.2 GDB编译程序1.3 启动GDB1.4 载入被调试程序1.5 查看源码1.6 运行程序1.7 断点设置1.7.1 通过行号设置断点1.7.2 通过函数名设置断点1.7.3 通过条件设置断点1.7.4 查看断点信息1.7.5 删除断点 1.8 单步调试1.9 2. GDB调试core文件2.1 设定core文件的…...

深入了解Java Duration类,对时间的精细操作
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概6000多字,预计阅读时间长需要5分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...

Python:核心知识点整理大全5-笔记
目录 2. 使用方法pop()删除元素 3. 弹出列表中任何位置处的元素 4. 根据值删除元素 3 章 列表简介 3.3 组织列表 3.3.1 使用方法 sort()对列表进行永久性排序 3.3.2 使用函数 sorted()对列表进行临时排序 3.3.3 倒着打印列表 3.3.4 确定列表的长度 3.5 小结 2. 使用方…...
、微调(fine-tuning)、迁移学习(transfer learning))
预训练(pre-learning)、微调(fine-tuning)、迁移学习(transfer learning)
预训练(pre-learning) 搭建一个网络模型来完成一个特定的图像分类的任务。首先,你需要随机初始化参数,然后开始训练网络,不断调整参数,直到网络的损失越来越小。在训练的过程中,一开始初始化的…...

王道数据结构课后代码题 p149 第8—— 12(c语言代码实现)
目录 8.假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。 9.设树B是一棵采用链式结构存储的二叉树,编写一个把树 B中所有结点的左、右子树进行交换的函数。 10.假设二叉树采用二叉链存储结构存储…...
Nginx服务优化以及防盗链
1. 隐藏版本号 以在 CentOS 中使用命令 curl -I http://192.168.66.10 显示响应报文首部信息。 查看版本号 curl -I http://192.168.66.10 1. 修改配置文件 vim /usr/local/nginx/conf/nginx.conf http {include mime.types;default_type application/octet-stream;…...

20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负 定义 7.1.1 设 A ( a i j ) ∈ R m n \boldsymbol{A}\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A(aij)∈Rmn, 如果 a i j ⩾ 0 , i 1 , ⋯ , m ; j 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i1, \cdots, m ; j1, \cd…...
Linux(centos)学习笔记(初学)
[rootlocalhost~]#:[用户名主机名 当前所在目录]#超级管理员标识 $普通用户的标识 Ctrlshift放大终端字体 Ctrl缩小终端字体 Tab可以补全命令 Ctrlshiftc/V复制粘贴 / :根目录,Linux系统起点 ls: #list列出目录的内容,通常用户查看…...

ECharts标题字体大小自适应变化
我们在做自适应Echarts的时候,字体大小在配置项里是如下配置的, title 标题组件,包含主标题和副标题。 以下是常用的对标题的设置: title:{//设置图表的标题text:"主标题",link:"baidu.com", //设置标题超链接target:"self",...
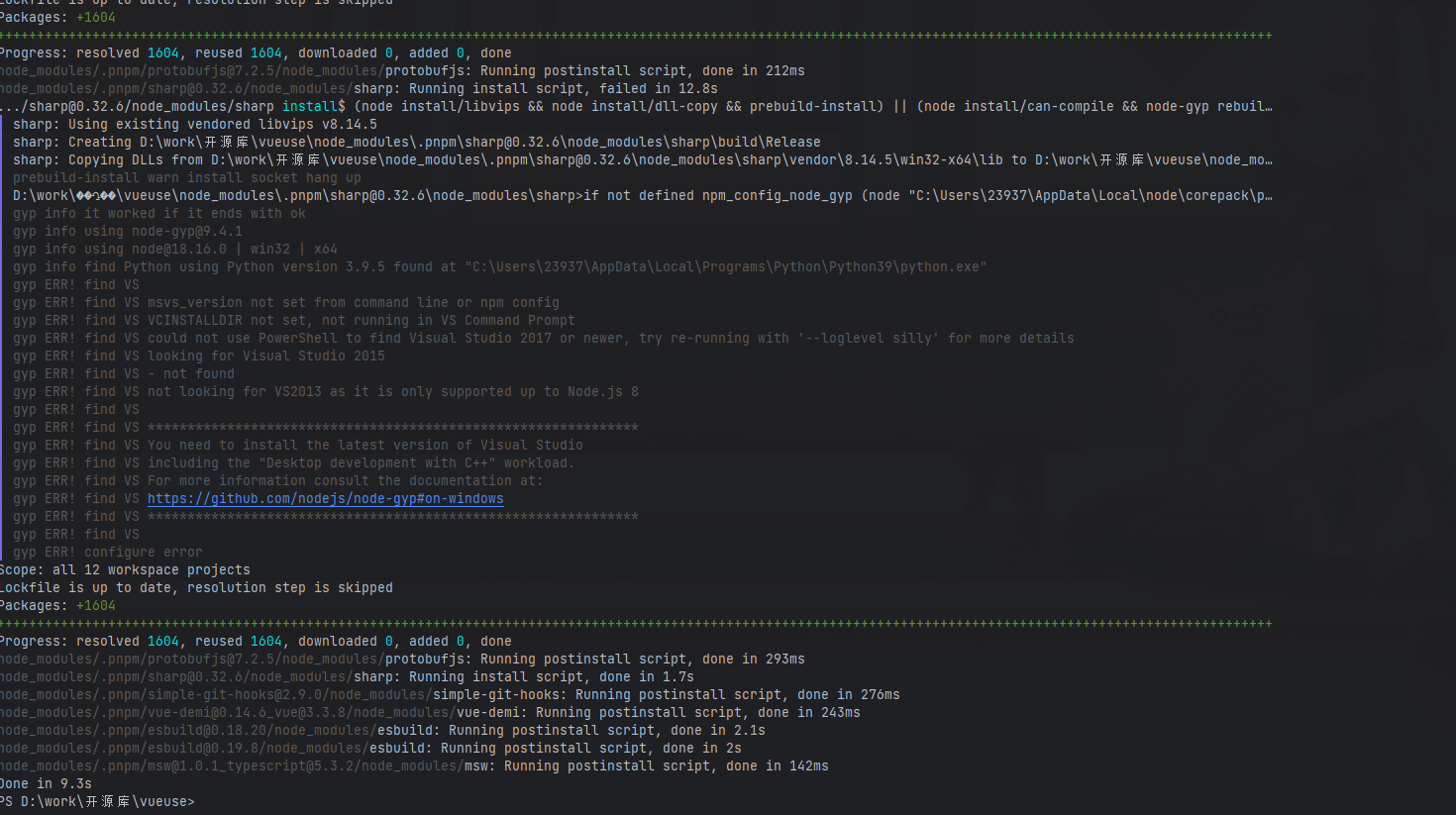
解决使用pnpm安装时Sharp模块报错的方法
在使用pnpm进行项目依赖安装的过程中,有时候会遇到Sharp模块报错的情况。Sharp是一个用于处理图像的Node.js模块,但它的安装可能会因为各种原因而失败,导致项目无法正常启动。本文将介绍这个问题的方法。 问题描述 解决方法 在命令行分别输…...

Redis 数据的持久化 RDB、AOF、RDB + AOF、No persistence 各自优缺点
文章目录 一、RDB (Redis Database)1.1 RDB 优势1.2 RDB 缺点1.3 RDB 如何工作1.4 RDB配置1.5 开启/关闭,RDB快照策略,save指令1.6 持久化硬盘文件,dbfilename指令1.7 持久化硬盘文件的存储地址,dir指令 二、AOF (Append Only Fil…...
回味童年经典游戏的项目
目录 1.超级玛丽2.坦克大战3.吃豆人游戏4.贪吃蛇游戏 1.超级玛丽 项目地址:超级马里奥游戏源码 在线试玩网址在资源描述中 在线试玩:http://martindrapeau.github.io/backbone-game-engine/super-mario-bros/index.html 主要语言:JavaScript…...

Electron[5] 渲染进程和主进程
1 进程 Electron里头的进程分为渲染进程和主进程。简单理解: main.js就是主进程每个页面就是渲染进程一个Electron应用仅有一个主进程,可以有多个渲染进程 上面的这些概念很重要,不展开细讲。 2 进程职责 主进程是用来实现应用的基础功能…...
基于Java SSM框架实现大学生校园兼职系统项目【项目源码+论文说明】
基于java的SSM框架实现大学生兼职系统演示 摘要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,大学生校园兼职系统当然也不能排除在外。大学生校园兼职系统是以实际运用为开…...
Codeforces Round 913 (Div. 3) A~E
目录 A. Rook 问题分析: B. YetnotherrokenKeoard 问题分析: C. Removal of Unattractive Pairs 问题分析: D. Jumping Through Segments 问题分析: E. Good Triples 问题分析: A. Rook 问题分析: 给一个棋子将其同行同列的位置输出 #include<bits/s…...

反序列化 [网鼎杯 2020 朱雀组]phpweb 1
打开题目 我们发现这个页面一直在不断的刷新 我们bp抓包一下看看 我们发现index.php用post方式传了两个参数上去,func和p 我们需要猜测func和p两个参数之间的关系,可以用php函数MD5测一下看看 我们在响应处得到了一串密文,md5解密一下看看 发…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
