20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负
定义 7.1.1 设 A = ( a i j ) ∈ R m × n \boldsymbol{A}=\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A=(aij)∈Rm×n, 如果
a i j ⩾ 0 , i = 1 , ⋯ , m ; j = 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i=1, \cdots, m ; j=1, \cdots, n, aij⩾0,i=1,⋯,m;j=1,⋯,n,
即 A \boldsymbol{A} A 的所有元素是非负的, 则称 A \boldsymbol{A} A 为非负矩阵, 记作 A ⩾ 0 \boldsymbol{A} \geqslant 0 A⩾0; 若式 (7.1.1) 中严格不等号成立, 即 a i j > 0 ( i = 1 , ⋯ , m ; j = 1 , ⋯ , n ) a_{i j}>0(i=1, \cdots, m ; j=1, \cdots, n) aij>0(i=1,⋯,m;j=1,⋯,n), 则称 A \boldsymbol{A} A 为正矩阵, 记为 A > 0 \boldsymbol{A}>0 A>0.
2. 随机矩阵:
定义 7.2.1 设 A = ( a i j ) ∈ R n × n \boldsymbol{A}=\left(a_{i j}\right) \in \mathbb{R}^{n \times n} A=(aij)∈Rn×n 是非负矩阵, 如果 A \boldsymbol{A} A 的每一行上的元素之和都等于 1 , 即
∑ j = 1 n a i j = 1 , i = 1 , 2 , ⋯ , n , \sum_{j=1}^n a_{i j}=1, \quad i=1,2, \cdots, n, j=1∑naij=1,i=1,2,⋯,n,
则称 A \boldsymbol{A} A 为随机矩阵; 如果 A \boldsymbol{A} A 还满足
∑ i = 1 n a i j = 1 , j = 1 , 2 , ⋯ , n , \sum_{i=1}^n a_{i j}=1, \quad j=1,2, \cdots, n, i=1∑naij=1,j=1,2,⋯,n,
则称 A \boldsymbol{A} A 为双随机矩阵.
定理 7.2.1 设 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n 是随机矩阵,则有
ρ ( A ) = 1. \rho(\boldsymbol{A})=1 . ρ(A)=1.
证明:谱半径 ρ \rho ρ 是矩阵最大特征值。因为 A \boldsymbol{A} A 是随机矩阵, 所以 A \boldsymbol{A} A 的每一行元素之和为 1 , 则 ∥ A ∥ ∥ ∞ = 1 \|\boldsymbol{A}\| \|_{\infty}=1 ∥A∥∥∞=1. 令 x = ( 1 , ⋯ , 1 ) T \boldsymbol{x}=(1, \cdots, 1)^{\mathrm{T}} x=(1,⋯,1)T, 显然 A x = x = ∥ A ∥ ∞ x \boldsymbol{A} \boldsymbol{x}=\boldsymbol{x}=\|\boldsymbol{A}\|_{\infty} \boldsymbol{x} Ax=x=∥A∥∞x, 即 x \boldsymbol{x} x 是 A \boldsymbol{A} A 对应于特征值 ∥ A ∥ ∞ \|\boldsymbol{A}\| \infty ∥A∥∞ 的特征向量, 而 ρ ( A ) ⩽ ∥ A ∥ ∞ \rho(\boldsymbol{A}) \leqslant\|\boldsymbol{A}\|_{\infty} ρ(A)⩽∥A∥∞, 同时又有 ∥ A ∥ ∞ ⩽ ρ ( A ) \|\boldsymbol{A}\|_{\infty} \leqslant \rho(\boldsymbol{A}) ∥A∥∞⩽ρ(A), 故得 ρ ( A ) = ∥ A ∥ ∞ = 1 \rho(\boldsymbol{A})=\|\boldsymbol{A}\|_{\infty}=1 ρ(A)=∥A∥∞=1.
证毕
定理 7.2.2 随机矩阵的乘积仍为随机矩阵。
闵可夫斯基(Minkovski)矩阵,简称M矩阵
定义 7.4.1 设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n, 且可表示为
A = s I − B , s > 0 , B ⩾ 0. \boldsymbol{A}=s \boldsymbol{I}-\boldsymbol{B}, \quad s>0, \quad \boldsymbol{B} \geqslant 0 . A=sI−B,s>0,B⩾0.
若 s ⩾ ρ ( B ) s \geqslant \rho(\boldsymbol{B}) s⩾ρ(B), 则称 A \boldsymbol{A} A 为 M \mathbf{M} M 矩阵; 若 s > ρ ( B ) s>\rho(\boldsymbol{B}) s>ρ(B), 则称 A \boldsymbol{A} A 为非奇异 M \mathbf{M} M 矩阵.
Q:为什么叫非奇异M矩阵?
A:因为M矩阵的每一个实特征值均为正。 ( s I − B ) x A = λ A x A (s\boldsymbol{I}-\boldsymbol{B})\boldsymbol{x}_A=\lambda_A\boldsymbol{x}_A (sI−B)xA=λAxA, λ A \lambda_A λA 和 x A \boldsymbol{x}_A xA 分别为矩阵 A \boldsymbol{A} A 的特征值和特征向量。那么 B x A = ( s − λ A ) x A \boldsymbol{B}\boldsymbol{x}_A=(s-\lambda_A)\boldsymbol{x}_A BxA=(s−λA)xA。反证法:加入 λ A \lambda_A λA为负数,那么 s − λ A > s > ρ ( B ) s-\lambda_A>s>\rho(\boldsymbol{B}) s−λA>s>ρ(B),上述等式不可能成立。因此 λ A \lambda_A λA为正数。
相关文章:

20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负 定义 7.1.1 设 A ( a i j ) ∈ R m n \boldsymbol{A}\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A(aij)∈Rmn, 如果 a i j ⩾ 0 , i 1 , ⋯ , m ; j 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i1, \cdots, m ; j1, \cd…...
Linux(centos)学习笔记(初学)
[rootlocalhost~]#:[用户名主机名 当前所在目录]#超级管理员标识 $普通用户的标识 Ctrlshift放大终端字体 Ctrl缩小终端字体 Tab可以补全命令 Ctrlshiftc/V复制粘贴 / :根目录,Linux系统起点 ls: #list列出目录的内容,通常用户查看…...

ECharts标题字体大小自适应变化
我们在做自适应Echarts的时候,字体大小在配置项里是如下配置的, title 标题组件,包含主标题和副标题。 以下是常用的对标题的设置: title:{//设置图表的标题text:"主标题",link:"baidu.com", //设置标题超链接target:"self",...
解决使用pnpm安装时Sharp模块报错的方法
在使用pnpm进行项目依赖安装的过程中,有时候会遇到Sharp模块报错的情况。Sharp是一个用于处理图像的Node.js模块,但它的安装可能会因为各种原因而失败,导致项目无法正常启动。本文将介绍这个问题的方法。 问题描述 解决方法 在命令行分别输…...

Redis 数据的持久化 RDB、AOF、RDB + AOF、No persistence 各自优缺点
文章目录 一、RDB (Redis Database)1.1 RDB 优势1.2 RDB 缺点1.3 RDB 如何工作1.4 RDB配置1.5 开启/关闭,RDB快照策略,save指令1.6 持久化硬盘文件,dbfilename指令1.7 持久化硬盘文件的存储地址,dir指令 二、AOF (Append Only Fil…...
回味童年经典游戏的项目
目录 1.超级玛丽2.坦克大战3.吃豆人游戏4.贪吃蛇游戏 1.超级玛丽 项目地址:超级马里奥游戏源码 在线试玩网址在资源描述中 在线试玩:http://martindrapeau.github.io/backbone-game-engine/super-mario-bros/index.html 主要语言:JavaScript…...

Electron[5] 渲染进程和主进程
1 进程 Electron里头的进程分为渲染进程和主进程。简单理解: main.js就是主进程每个页面就是渲染进程一个Electron应用仅有一个主进程,可以有多个渲染进程 上面的这些概念很重要,不展开细讲。 2 进程职责 主进程是用来实现应用的基础功能…...
基于Java SSM框架实现大学生校园兼职系统项目【项目源码+论文说明】
基于java的SSM框架实现大学生兼职系统演示 摘要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,大学生校园兼职系统当然也不能排除在外。大学生校园兼职系统是以实际运用为开…...
Codeforces Round 913 (Div. 3) A~E
目录 A. Rook 问题分析: B. YetnotherrokenKeoard 问题分析: C. Removal of Unattractive Pairs 问题分析: D. Jumping Through Segments 问题分析: E. Good Triples 问题分析: A. Rook 问题分析: 给一个棋子将其同行同列的位置输出 #include<bits/s…...

反序列化 [网鼎杯 2020 朱雀组]phpweb 1
打开题目 我们发现这个页面一直在不断的刷新 我们bp抓包一下看看 我们发现index.php用post方式传了两个参数上去,func和p 我们需要猜测func和p两个参数之间的关系,可以用php函数MD5测一下看看 我们在响应处得到了一串密文,md5解密一下看看 发…...
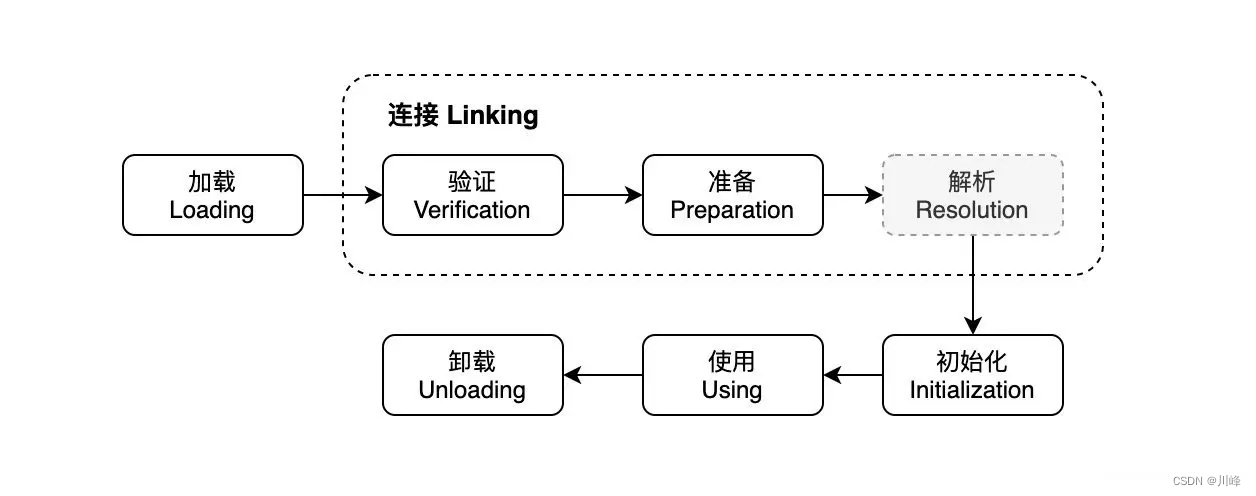
Java 何时会触发一个类的初始化
Java 何时会触发一个类的初始化? 使用new关键字创建对象访问类的静态成员变量 或 对类的静态成员变量进行赋值调用类的静态方法反射调用类时,如 Class.forName()初始化子类时,会先初始化其父类(如果父类还没有进行过初始化的话&a…...

我的记事本
url uniform resource locator. 统一资源定位符 请求状态码 1XX:信息响应 2XX:成功响应 3XX:重定向消息 4XX:客户端错误响应 5XX:服务器端错误响应 IP地址分类 本机回环IP地址:127.0.0.1 ~ 127.255.255.254 局域网IP(私网IP) 192.168.0.0 &am…...
)
GO设计模式——4、单例模式(创建型)
目录 单例模式(Singleton Pattern) 优缺点 使用场景 饿汉式和懒汉式单例模式 单例模式(Singleton Pattern) 单例模式(Singleton Pattern)是一个类只允许创建一个对象(或者实例ÿ…...

我对迁移学习的一点理解——领域适应(系列3)
文章目录 1. 领域适应(Domain Adaptation)的基本概念2.领域适应(Domain Adaptation)的目标3.领域适应(Domain Adaptation)的实现方法4.领域适应(Domain Adaptation)的可以解决的问题…...
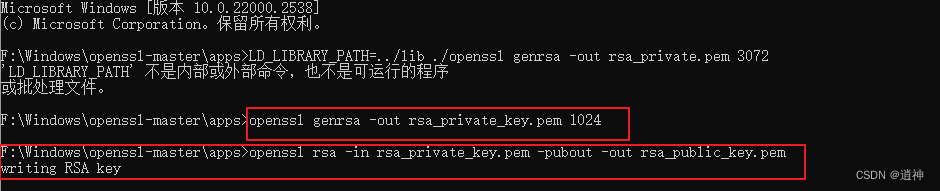
【openssl】RSA 生成公钥私钥 |通过私钥获取公钥
通过博客:Window系统如何编译openssl 编译出openssl.exe(位于apps文件夹下)。 现在需要使用它获得公钥私钥、通过私钥获取公钥 目录 说明!!! 一.定位openssl.exe目录 二、进入命令cmd 三、生成私钥 …...

MongoDB的删除文档、查询文档语句
本文主要介绍MongoDB的删除文档、查询文档命令语句。 目录 MongoDB删除文档MongoDB查询文档 MongoDB删除文档 MongoDB是一种基于文档的NoSQL数据库,它使用BSON格式存储文档。删除文档是MongoDB数据库中的常见操作之一。 下面是MongoDB删除文档的详细介绍和示例&am…...
-trait)
Rust编程语言入门教程(三)-trait
文章目录 Rust编程语言入门教程(三)-trait什么是 trait?trait使用举例 Rust编程语言入门教程(三)-trait 什么是 trait? trait 是 Rust 中的接口,它定义了类型使用这个接口的行为。你可以类比到…...

LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】
LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】 题目描述:解题思路一:题意就是找出长度为m且连续重复k次的子数组。解题思路就是暴力枚举加剪枝。解题思路二:思路差不多解题思路三:0 题目描述: 给你一个…...
QT5.4.1无法打开文件
问题描述:起初是在QT代码中运行打开文件代码: QString gFilename QFileDialog::getOpenFileName(this,"open File",path,"*", nullptr,QFileDialog::DontUseNativeDialog);时,出现了堵塞情况,经过多次实验一…...

【1day】金和OA某接口存在未授权访问漏洞
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
