【计算机考研408】快速排序的趟数问题 + PAT 甲级 7-2 The Second Run of Quicksort
前言
该题还未加入PAT甲级题库中,可以通过购买2022年秋季甲级考试进行答题,纯考研题改编
快速排序
常考的知识点
- 快速排序是基于分治法
- 快速排序是所有内部排序算法中平均性能最优的排序算法
- 快速排序是一种不稳定的排序算法
- 快速排序算法中,不产生有序子序列,但每趟排序后会将枢轴元素放到其最终位置上
基于分治的思想,主要由两个步
1)划分
2)排序
代码
void QSort(int A[], int L, int R){if(L >= R) return;int key = A[L + R >> 1]; //选取L,R中间的元素作为基准int i = L - 1, j = R + 1;whiLe(i < j){do i ++; whiLe(A[i] < key); //左指针右移,找到比基准大的数do j --; whiLe(A[j] > key); //右指针左移,找到比基准小的数if(i < j) swap(A,i,j); //交换A[i]和A[j] }QSort(A, L ,j);QSort(A, j + 1, R);
}
void quicksort(int a[], int low, int high){if (low < high){int pos = partition(a, low, high);quicksort(a, low, pos-1);quicksort(a, pos+1, high);}
}
//partition是一趟排序
int partition(int a[], int low, int high){int pos = a[low];//将表中第一个元素设置位枢轴while(low < high){//从右边找到第一个比枢轴值小的while(low < high && a[high] >= pos) --high;a[low] = a[high];while(low < high && a[low] >= pos) ++low;a[high] = a[low];}a[low] = pos;return low;
}
题源-2019年考研选择题

分析
- 两次排序,说明起码有两个中枢元素在最终的位置上,若小于两个元素在最终位置上,那么一定不是两趟快速排序
- 若出现两个或者两个以上的元素位于最终位置上,那么起码有一个元素要位于序列的第一个位置或者是最后一个位置
注意题目中的提示,两种类型的题目,(1)分类讨论直接有结果的(2)模拟流程进行解答
测试数据
输入
4
8
5 2 16 12 28 60 32 72
8
2 16 5 28 12 60 32 72
8
2 12 16 5 28 32 72 60
8
5 2 12 28 16 32 72 60
输出
Yes
Yes
Yes
No
//判断是不是快速排序的第二轮
#include <bits/stdc++.h>
using namespace std;
int main(){int T; cin >> T;for(int t = 1; t <= T; t++){int n; cin >> n;vector<int> arr(n), tmp(n);for(int i = 0; i < n; i++){cin >> arr[i];tmp[i] = arr[i];}sort(tmp.begin(), tmp.end());vector<int> p;for(int i = 0; i < n; i++){if (arr[i] == tmp[i]) {p.push_back(i);}}if (p.size() < 2){cout << "No" << '\n'; //continue;}else {if (p[0] == 0 || p[p.size() - 1] == n - 1) {cout << "Yes" << '\n';}else {cout << "No" << '\n';}}}
}
相关文章:

【计算机考研408】快速排序的趟数问题 + PAT 甲级 7-2 The Second Run of Quicksort
前言 该题还未加入PAT甲级题库中,可以通过购买2022年秋季甲级考试进行答题,纯考研题改编 快速排序 常考的知识点 快速排序是基于分治法快速排序是所有内部排序算法中平均性能最优的排序算法快速排序是一种不稳定的排序算法快速排序算法中,…...
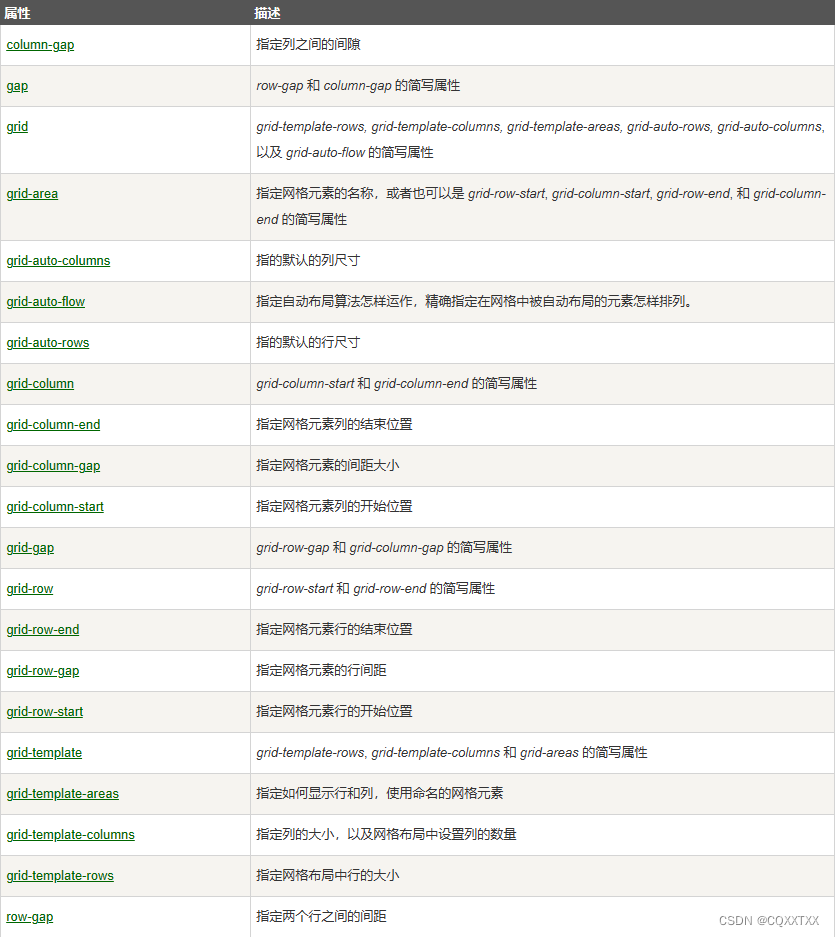
CSS-Grid(网格)布局
前言 之前HTML 页面的布局基本上都是通过 Flexbox 来实现的,能轻松的解决复杂的 Web 布局。 现在又出现了一个构建 HTML 最佳布局体系的新竞争者。就是强大的CSS Grid 布局。 grid和flex区别是什么?适用什么场景? Flexbox 是一维布局系统&am…...

软件测试4
一 form表单标签 1.form表单标签里面就是所有用户填写的表单数据; action“xxx.py”把表单数据提交给哪一个后台程序去处理 method“post” 传递数据时候的方式方法,post代表隐式提交数据、get明文传送数据 2.input标签的type类型 type“text” 普通的输…...

996的压力下,程序员还有时间做副业吗?
996怎么搞副业? 这个问题其实蛮奇怪的:996的压力下,怎么会还想着搞副业呢? 996还想搞副业的原因有哪些? 大家对于996应该都不陌生,总结就是一个字:忙。 996的工作性质就是加班,就…...

每日学术速递3.1
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Directed Diffusion: Direct Control of Object Placement through Attention Guidance 标题:定向扩散:通过注意力引导直接控制物体放置 作者:…...
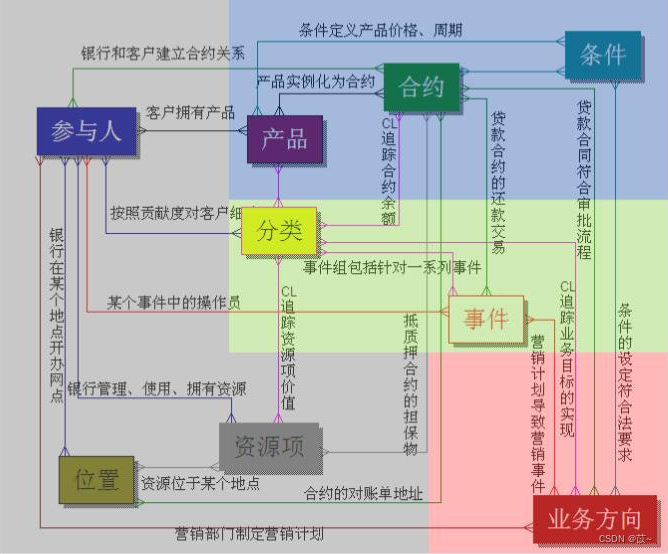
金融行业数据模型
一、Teradata FS-LDM Teradata 公司基于金融业务发布的FS-LDM(Financial Servies Logical Data Model) 十大主题:当事人、产品、协议、事件、资产、财务、机构、地域、营销、渠道。 1、当事人(Party) 银行所服务的任…...

【面试题】2023前端vue面试题及答案
Vue3.0 为什么要用 proxy?在 Vue2 中, 0bject.defineProperty 会改变原始数据,而 Proxy 是创建对象的虚拟表示,并提供 set 、get 和 deleteProperty 等处理器,这些处理器可在访问或修改原始对象上的属性时进行拦截&…...
leetcode128. 最长连续序列)
(哈希查找)leetcode128. 最长连续序列
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。…...

js中splice方法和slice方法
splice方法用来操作数组splice(startIndex,deleteNum,item1,....,)此操作会改变原数组。删除数组中元素参数解释:startIndex为起始index索引。deleteNum为从startIndex索引位置开始需要删除的个数。分三种情况:没有传第三个参数的情况下,dele…...

c++ argparse
需求 c程序传参数,像python中argparse一样方便。 方法1 用gflags 参考https://heroacool.blog.csdn.net/?typeblog git clone https://github.com/gflags/gflags cd gflags # 进入项目文件夹 cmake . # 使用 cmake 编译生成 Makefile 文件 make -j 24 # make 编…...

内大892复试真题16年
内大892复试真题16年 1. 输出三个数中较大数2. 求两个数最大公约数与最小公倍数3. 统计字符串中得字符个数4. 输出菱形5. 迭代法求平方根6. 处理字符串(逆序、进制转换)7. 寻找中位数8. 输入十进制输出n进制1. 输出三个数中较大数 问题 代码 #include <iostream>usin…...

面试题 05.02. 二进制数转字符串
二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。 示例1: 输入:0.625输出:"0…...

MySQL数据更新操作
文章目录前言添加数据插入数据删除数据修改数据前言 提示:这里可以添加本文要记录的大概内容: 数据更新有两种办法: 1:使用数据可视化工具操作 2:SQL语句 添加数据 前面的添加数据命令一次只能插入一条记录。如果想…...

C# 封装
修正bug之前总是要考虑是什么导致了这个bug,并花些时间了解发生了什么。增加打印输出行的语句可能是一个很有效的调试工具。增加语句来打印诊断信息时,要使用Debug.WriteLine。构造器是CLR第一次创建一个新对象实例时调用的方法。字符串插值会让字符串拼…...

每日学术速递3.2
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Interactive Segmentation as Gaussian Process Classification(CVPR 2023) 标题:作为高斯过程分类的交互式分割 作者:Minghao Zhou, Hong Wang, Qian Zha…...

PCBA方案设计——LCD体重电子秤方案
体重秤,一种测量体重的电子秤,与最近很火的体脂秤来比来说,他是的功能能就有点单一了,只能测量体重,而体脂秤可以精准抓取测量体脂体重等一系列的数据,功能更为多样,但相比之下体重秤的功能简单…...

动态规划--背包问题
动态规划背包问题算法思路代码实现背包问题 假设你要去野营。你有一个容量为6磅的背包,需要决定该携带下面的哪些东西。其中每样东西都有相应的价值,价值越大意味着越重要: 水(重3磅,价值10) 书&…...

从0开始学python -45
Python3 正则表达式 -3 正则表达式对象 re.RegexObject re.compile() 返回 RegexObject 对象。 re.MatchObject group() 返回被 RE 匹配的字符串。 start() 返回匹配开始的位置end() 返回匹配结束的位置span() 返回一个元组包含匹配 (开始,结束) 的位置 正则表达式修饰符…...
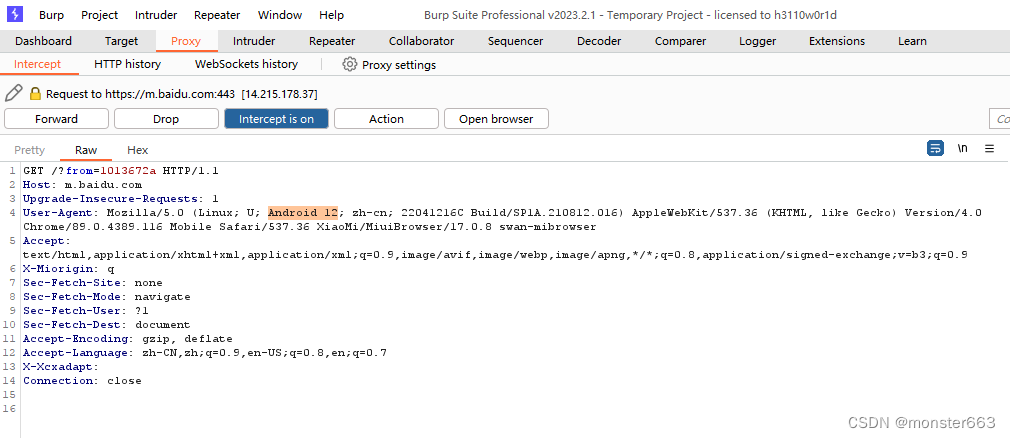
如何用BurpSuite抓取手机数据包
文章目录前言准备工具Burp Suite物理机或虚拟机(移动设备)手机抓包网络环境开启burp并设置代理手机配置代理安装Burp证书开始抓包踩坑后记前言 最近挖了一波src,挖来挖去发现有很多公众号或者app没有测试,这就需要Burp能够抓取手机的数据包了࿰…...

Linux性能监控工具iostat解析
1.iostat命令详解 CPU 内存 磁盘 网络 四大子系统 1.1 查看提供iostat命令的软件包 yum provides "*/iostat" yum -y install systatiostat 1 显示实时的数据 iostat 结果自系统启动以来的平均值1.2 iostat命令CPU指标 %user 应用程序消耗CPU资源占比 %nice 进…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
