202309-2
http://118.190.20.162/view.page?gpid=T174
题目分析:
这道题读完题后感觉像是考察前缀和,这里回顾下什么是前缀和:https://blog.csdn.net/weixin_45629285/article/details/111146240

我们利用前缀和算法,就可以在O(n+m)的时间内完成。
具体分析一下怎么套前缀和模板;
我们只要画个图,就可以发现
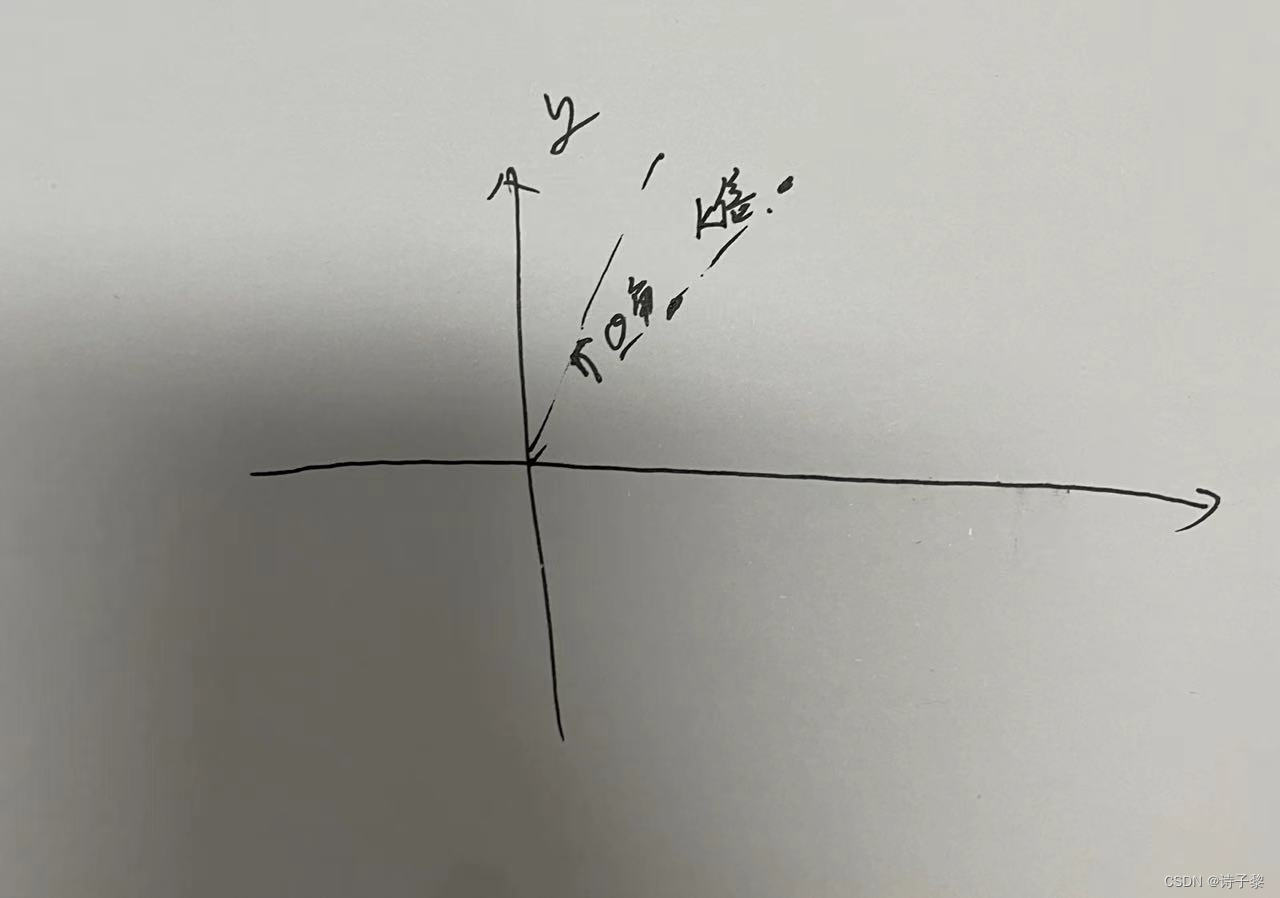
每次旋转的角度和扩大的倍数这两个操作,是彼此独立的,因此我们可以用两个前缀和数组,sum1和sum2,分别记录拉伸k倍和旋转。
代码如下:
#include <iostream>
#include <cmath>using namespace std;const int MAXN = 1e6+5;double k[MAXN] = {1};
double theta[MAXN] = {0.0};
double sumk[MAXN];
double sumTheta[MAXN] = {0};int main() {for (int i = 0;i < MAXN;i++)k[i] = 1,sumk[i] = 1;
// std::cout << "Hello, World!" << std::endl;int n, m;scanf("%d%d",&n,&m);for(int i = 1; i <= n; i++){int op;scanf("%d",&op);if(op == 1){scanf("%lf", &k[i]);}else{scanf("%lf",&theta[i]);}sumk[i] = sumk[i-1]*k[i];
// printf("%f",sumk[i]);sumTheta[i] = sumTheta[i - 1] + theta[i];}for(int i = 1; i <= m; ++i){int l, r, x, y;scanf("%d%d%d%d",&l,&r,&x,&y);double tx, ty;double tk = sumk[r] / sumk[l - 1];double ttheta = sumTheta[r] - sumTheta[l - 1];tx = tk * x;ty = tk * y;double ansx, ansy;ansx = tx * cos(ttheta) - ty * sin(ttheta);ansy = tx * sin(ttheta) + ty * cos(ttheta);printf("%f %f\n", ansx, ansy);}return 0;}结果:

相关文章:

202309-2
http://118.190.20.162/view.page?gpidT174 题目分析: 这道题读完题后感觉像是考察前缀和,这里回顾下什么是前缀和:https://blog.csdn.net/weixin_45629285/article/details/111146240 我们利用前缀和算法,就可以在O(nm)的时…...
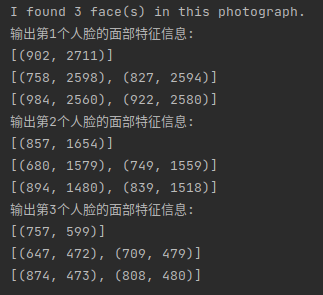
数字图像处理(实践篇)二十 人脸特征提取
目录 1 安装face_recognition 2 涉及的函数 3 实践 使用face_recognition进行人脸特征提取. 1 安装face_recognition pip install face_recognition 或者 pip --default-timeout100 install face_recognition -i http://pypi.douban.com/simple --trusted-host pypi.dou…...
Python自动化:selenium常用方法总结
使用的Python版本为3.8,selenium版本为4.15.2 Python自动化:selenium常用方法总结 1. 三种等待方式2. 浏览器操作3. 8种查找元素的方法4. 高级事件 1. 三种等待方式 强制等待 使用模块time下的sleep()实现等待效果隐式等待 使用driver.implicitly_wait()方法&#…...
『开源资讯』JimuReport积木报表 v1.6.6 版本发布—免费报表工具
项目介绍 一款免费的数据可视化报表,含报表和大屏设计,像搭建积木一样在线设计报表!功能涵盖,数据报表、打印设计、图表报表、大屏设计等! Web 版报表设计器,类似于excel操作风格,通过拖拽完成报…...

每天五分钟计算机视觉:使用1*1卷积层来改变输入层的通道数量
本文重点 在卷积神经网络中有很多重要的卷积核,比如1*1的卷积核,3*3的卷积核,本文将讲解1*1的卷积核的使用,它在卷积神经网络中具有重要的地位。由于1*1的卷积核使用了最小的窗口,那么1*1的卷积核就失去了卷积层可以识…...

Java (JDK 21) 调用 OpenCV (4.8.0)
Java 调用 OpenCV 一.OpenCV 下载和安装二.创建 Java Maven 项目三.其他测试 一.OpenCV 下载和安装 Open CV 官网 可以下载编译好的包,也可以下载源码自行编译 双击安装 opencv-4.8.0-windows.exe 默认为当前目录 安装即解压缩 根据系统位数选择 将 x64 目录下 op…...

git 常用的使用方法
1.查看分支 $ git branch #查看本地分支 $ git branch -r #查看远程分支 $ git branch -a #查看所有分支 $ git branch -vv #查看本地分支及追踪的分支 2.创建分支 方法1 $ git branch 分支名 #创建本地分支 #将本地分支push,就创建了远程分支方法2 #创建本地分…...
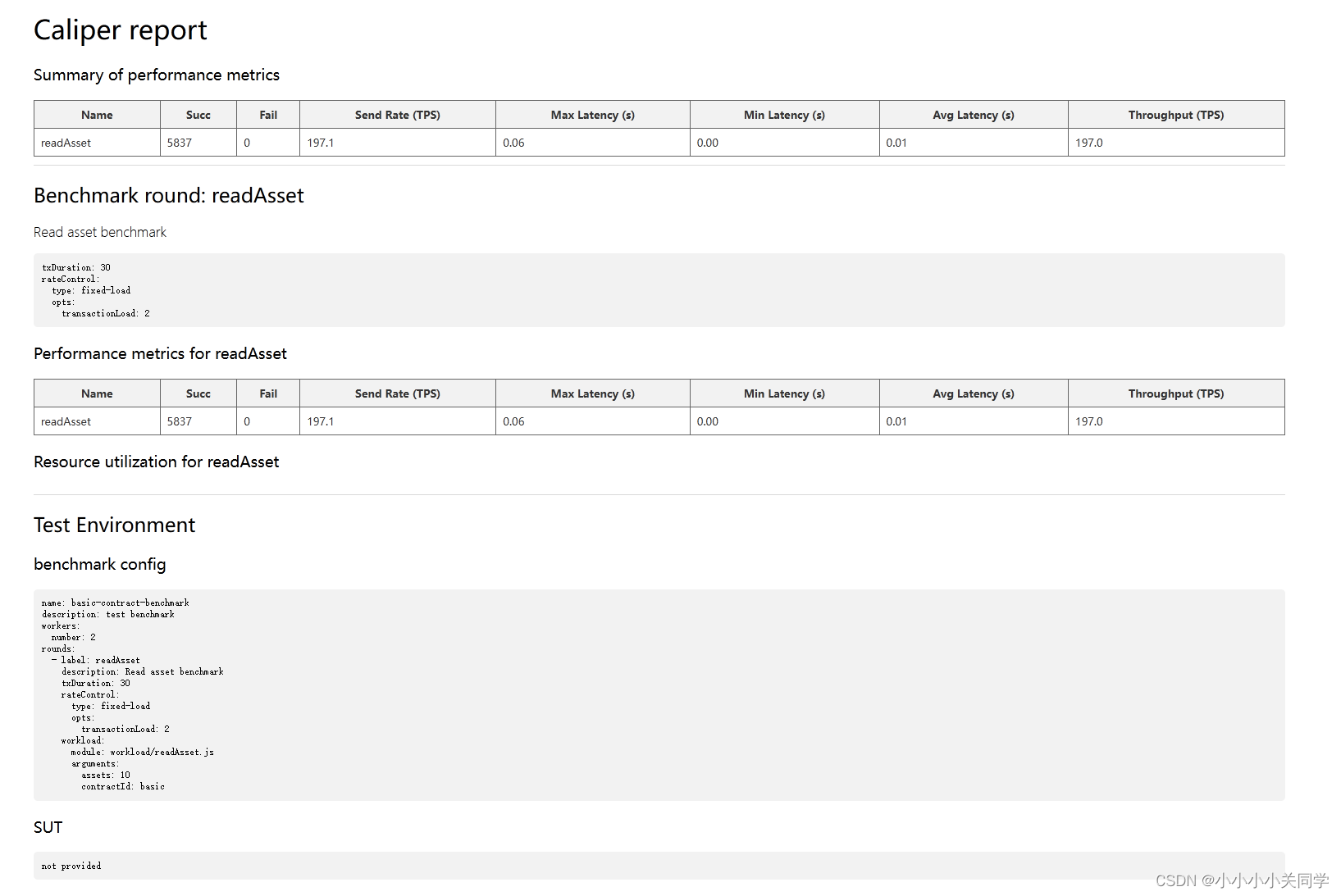
使用Caliper对Fabric地basic链码进行性能测试
如果你需要对fabric网络中地合约进行吞吐量、延迟等性能进行评估,可以使用Caliper来实现,会返回给你一份网页版的直观测试报告。下面是对test-network网络地basic链码地测试过程。 目录 1. 建立caliper-workspace文件夹2. 安装npm等3. calipe安装4. 创建…...

一台是阿里云,一台是腾讯云,一台是华为云,一台是百度云等多种公有云混合安装K8S集群
1. 修改主机名称和添加hosts #永久修改主机名 hostnamectl set-hostname master && bash #在master01上操作,阿里云服务器 hostnamectl set-hostname worker1 && bash #在node01上操作,阿里腾讯云服务器 hostnamectl set-ho…...

期末速成数据库极简版【查询】(3)
目录 多表查询 【8】多表连接——内连接 🙂等值连接 🙂自然连接 🙂非等值连接 【9】多表连接——外连接 【10】交叉连接不考 【11】联合查询 【12】扩展多表连接 【13】嵌套查询 🙂 多表查询 【8】多表连接——内连…...

人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101
然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而, 构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题. 比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值. 可以看到,这个带有一个不等式的条件,…...

有关光伏电站绝缘阻抗异常排查分析-安科瑞 蒋静
近几年,光伏发电技术迅猛发展,光伏扶贫电站及分布式光伏使光伏发电走进千家万户。然而光伏发电设备运行期间仍存在隐患。及时发现并解决*常见异常运行故障,可以很大地提高光伏发电设备可利用率,是保证光伏发电设备正常运行、满足收…...

抓取真实浏览器设备指纹fingerprint写入cookie方案
一个关于抓取真实浏览器设备指纹写入cookie方案,用户访问页面获取到用户设备生成指纹id,通过js把指纹存入cookie,然后用php进行获取cookie存的指纹值到后台。 用途:追踪用户设备,防恶意注册,防恶意采集 浏…...

【华为OD题库-074】VLAN资源池-Java
题目 VLAN是一种对局域网设备进行逻辑划分的技术,为了标识不同的VLAN,引入VLAN ID(1-4094之间的整数)的概念。定义一个VLAN ID的资源池(下称VLAN资源池),资源池中连续的VLAN用开始VLAN-结束VLAN表示,不连续的用单个整数表示&#…...
成都工业学院Web技术基础(WEB)实验一:HTML5排版标签使用
写在前面 1、基于2022级计算机大类实验指导书 2、代码仅提供参考,前端变化比较大,按照要求,只能做到像,不能做到一模一样 3、图片和文字仅为示例,需要自行替换 4、如果代码不满足你的要求,请寻求其他的…...

OpenAI承认ChatGPT变懒惰,正在修复该问题
OpenAI旗下的官方ChatGPT账号在社交平台表示,已经收到了大量用户关于GPT-4变懒惰的反馈。 这是因为自11月11日以来,OpenAI就没有更新过该模型。当然这不是故意的,大模型的行为是不可预测的,正在研究修复该问题。 外界猜测&#x…...
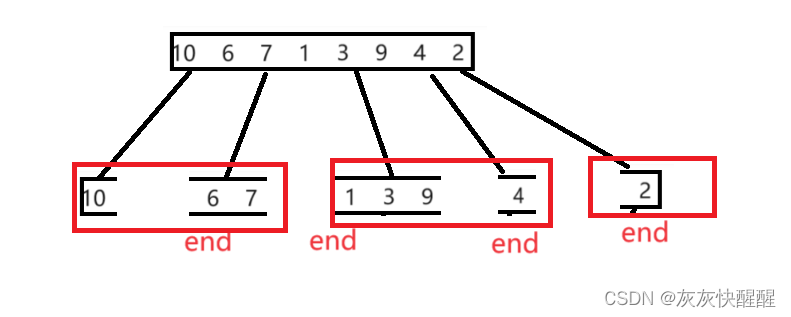
归并排序与自然归并排序
归并排序 归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并. 核心步骤讲解 归并排序的…...

22款奔驰GLS450升级HUD抬头显示 告别低头
随着科技飞速地发展,从汽车领域就可以看出,尤其是汽车的抬头显示器,一经推出就吸引了很多的车主。星骏汇小许Xjh15863 升级HUD抬头显示,HUD与汽车系统进行完整的数据信息连接,整合成大数据,然后将一些重要信…...

关于kotlin的属性委托,报错的,实际原因剖析
报错:Property delegate must have a ‘getValue(SecurityCheckView, KProperty*>)’ method. None of the following functions are suitable 解决方案:就是在根目录的build.gradle中改变 kotlin的插件版本 classpath “org.jetbrains.kotlin:kotli…...
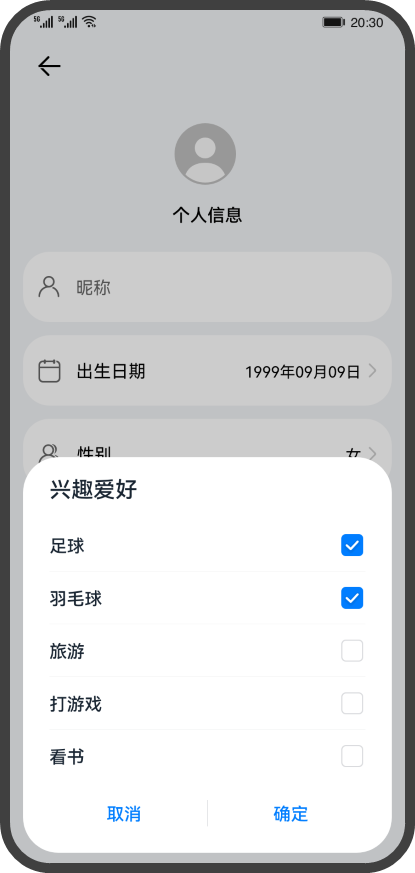
HarmonyOS4.0从零开始的开发教程11给您的应用添加弹窗
HarmonyOS(十)给您的应用添加弹窗 概述 在我们日常使用应用的时候,可能会进行一些敏感的操作,比如删除联系人,这时候我们给应用添加弹窗来提示用户是否需要执行该操作,如下图所示: 弹窗是一种…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
