当前位置： 首页 > news >正文

人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101

news 2026/2/6 3:08:23

然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而,

构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题.

比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值.

可以看到,这个带有一个不等式的条件,那么这种的如何求呢

我们可以回去看看拉格朗日乘子法的公式,可以看到是一个等式条件,这个时候可以,引入拉格朗日乘子,构建拉格朗日乘子法公式,来进行求解,但是不等式怎么做呢?

我们可以看到,这个时候,我们可以引入一个,松弛变量,可以看到这个松弛变量,我们让他是阿尔法,

然后添加一个阿尔法的平方,因为我们知道h(x)<=0 是小于=0的,所以我们就可以加一个大于等于0的数,那么这样就可以让h(x) + 阿尔法 ^2 = 0了,因为这里的阿尔法是加了平方,肯定是大于0的.

有了等式以后,这个时候我们就可以转换一下,使用拉格朗

相关文章：

人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101

然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而, 构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题. 比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值. 可以看到,这个带有一个不等式的条件,…...

编程日记 2023/12/11 12:18:49

有关光伏电站绝缘阻抗异常排查分析-安科瑞 蒋静

近几年&#xff0c;光伏发电技术迅猛发展&#xff0c;光伏扶贫电站及分布式光伏使光伏发电走进千家万户。然而光伏发电设备运行期间仍存在隐患。及时发现并解决*常见异常运行故障&#xff0c;可以很大地提高光伏发电设备可利用率&#xff0c;是保证光伏发电设备正常运行、满足收…...

编程日记 2023/12/11 12:17:49

抓取真实浏览器设备指纹fingerprint写入cookie方案

一个关于抓取真实浏览器设备指纹写入cookie方案&#xff0c;用户访问页面获取到用户设备生成指纹id&#xff0c;通过js把指纹存入cookie&#xff0c;然后用php进行获取cookie存的指纹值到后台。 用途&#xff1a;追踪用户设备&#xff0c;防恶意注册&#xff0c;防恶意采集 浏…...

编程日记 2023/12/11 12:16:48

【华为OD题库-074】VLAN资源池-Java

题目 VLAN是一种对局域网设备进行逻辑划分的技术&#xff0c;为了标识不同的VLAN&#xff0c;引入VLAN ID(1-4094之间的整数)的概念。定义一个VLAN ID的资源池(下称VLAN资源池)&#xff0c;资源池中连续的VLAN用开始VLAN-结束VLAN表示&#xff0c;不连续的用单个整数表示&#…...

编程日记 2023/12/11 12:15:47

成都工业学院Web技术基础（WEB）实验一：HTML5排版标签使用

写在前面 1、基于2022级计算机大类实验指导书 2、代码仅提供参考&#xff0c;前端变化比较大&#xff0c;按照要求&#xff0c;只能做到像&#xff0c;不能做到一模一样 3、图片和文字仅为示例&#xff0c;需要自行替换 4、如果代码不满足你的要求&#xff0c;请寻求其他的…...

编程日记 2023/12/11 12:08:41

OpenAI承认ChatGPT变懒惰，正在修复该问题

OpenAI旗下的官方ChatGPT账号在社交平台表示&#xff0c;已经收到了大量用户关于GPT-4变懒惰的反馈。 这是因为自11月11日以来&#xff0c;OpenAI就没有更新过该模型。当然这不是故意的&#xff0c;大模型的行为是不可预测的&#xff0c;正在研究修复该问题。 外界猜测&#x…...

编程日记 2023/12/11 12:04:37

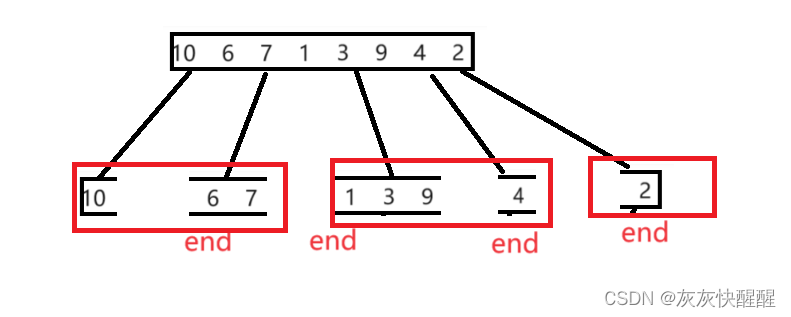
归并排序与自然归并排序

归并排序 归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并. 核心步骤讲解 归并排序的…...

编程日记 2023/12/11 12:03:37

22款奔驰GLS450升级HUD抬头显示 告别低头

随着科技飞速地发展&#xff0c;从汽车领域就可以看出&#xff0c;尤其是汽车的抬头显示器&#xff0c;一经推出就吸引了很多的车主。星骏汇小许Xjh15863 升级HUD抬头显示&#xff0c;HUD与汽车系统进行完整的数据信息连接&#xff0c;整合成大数据&#xff0c;然后将一些重要信…...

编程日记 2023/12/11 12:01:35

关于kotlin的属性委托，报错的，实际原因剖析

报错&#xff1a;Property delegate must have a ‘getValue(SecurityCheckView, KProperty*>)’ method. None of the following functions are suitable 解决方案&#xff1a;就是在根目录的build.gradle中改变 kotlin的插件版本 classpath “org.jetbrains.kotlin:kotli…...

编程日记 2023/12/11 12:00:34

HarmonyOS4.0从零开始的开发教程11给您的应用添加弹窗

HarmonyOS&#xff08;十&#xff09;给您的应用添加弹窗 概述 在我们日常使用应用的时候&#xff0c;可能会进行一些敏感的操作&#xff0c;比如删除联系人&#xff0c;这时候我们给应用添加弹窗来提示用户是否需要执行该操作&#xff0c;如下图所示&#xff1a; 弹窗是一种…...

编程日记 2023/12/11 11:57:32

js 同步任务和异步任务

同步任务和异步任务 同步任务 同步任务就是没有被引擎挂起、在主线程上排队执行的任务。只有前一个任务执行完&#xff0c;才会执行下一个任务。同步任务具有堵塞效果。 异步任务 异步任务是被引擎放在一边&#xff0c;不进入主线程进入任务队列的任务。只有引擎认为某个异步任…...

编程日记 2023/12/11 11:55:31

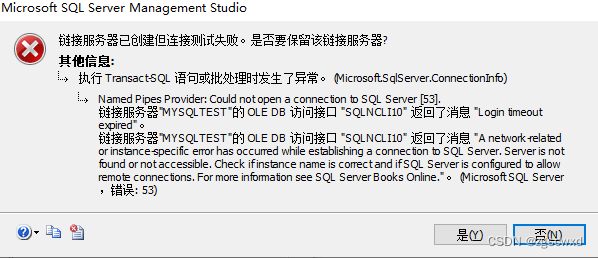
【小白专用】Sql Server 连接Mysql 更新23.12.09

目标 已知mysql连接参数&#xff08;地址和用户&#xff09;&#xff0c;期望通过Microsoft Sql Server Management Studio &#xff08;以下简称MSSSMS&#xff09;连接Mysql&#xff0c;在MSSSMS中直接查询或修改Mysql中的数据。 一般是选最新的版本下载。 选64位还是32位&a…...

编程日记 2023/12/11 11:54:30

DIP——边缘提取与分割

1.使用canny算法进行边缘提取 本实验比较简单&#xff0c;基本思路是对原图像进行一个高斯模糊处理&#xff0c;用于去噪&#xff0c;之后转换为灰度图&#xff0c;直接调用cv库中的canny记性边缘提取。若想直接得到彩色边缘&#xff0c;则通过按位与操作&#xff0c;将原始彩色…...

编程日记 2023/12/11 11:53:29

低代码开发：现实挑战与发展前景

低代码开发是近年来迅速崛起的软件开发方法&#xff0c;让编写应用程序变得更快、更简单。有人说它是美味的膳食&#xff0c;让开发过程高效而满足&#xff0c;但也有人质疑它是垃圾食品&#xff0c;缺乏定制性与深度。 一、什么是低代码 低代码开发是一种基于图形用户界面&…...

编程日记 2023/12/11 11:52:28

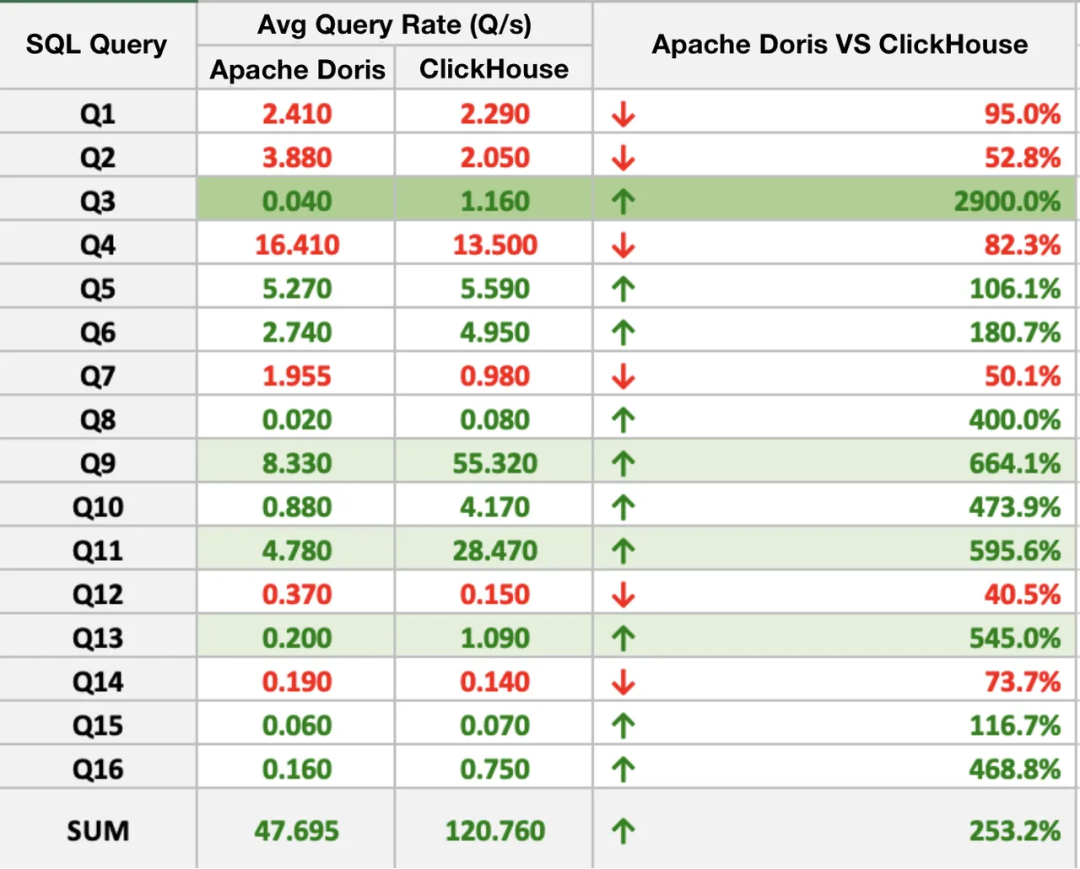
大数据技术7：基于StarRocks统一OALP实时数仓

前言&#xff1a; 大家对StarRocks 的了解可能不及 ClickHouse或者是远不及 ClickHouse 。但是大家可能听说过 Doris &#xff0c;而 StarRocks 实际上原名叫做 Doris DB &#xff0c;他相当于是一个加强版的也就是一个 Doris ,也就是说 Doris 所有的功能 StarRocks 都是有的&a…...

编程日记 2023/12/11 11:50:26

C# WPF上位机开发（网络程序界面开发）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 之前我们讨论过&#xff0c;设备之间通讯的方式很多。但是&#xff0c;不知道大家有没有注意&#xff0c;前面谈到的这些通讯方式都需要上位机电脑…...

编程日记 2023/12/11 11:49:25

卡码网语言基础课 | 20. 排队取奶茶

目录 一、 队列的基本认识 二、 队列的操作 2.1 引入头文件 2.2 创建队列 2.3 队列的常见操作 三、 解题 通过本次练习&#xff0c;将会学习到以下C知识点&#xff1a; 队列的基本概念&#xff08;队头、队尾&#xff09;和特点&#xff08;先入先出&#xff09;入队、出队…...

编程日记 2023/12/11 11:48:25

Angular 进阶之四：SSR 应用场景与局限

应用场景 内容丰富&#xff0c;复杂交互的动态网页&#xff0c;对首屏加载有要求的项目&#xff0c;对 seo 有要求的项目&#xff08;因为服务端第一次渲染的时候&#xff0c;已经把关键字和标题渲染到响应的 html 中了&#xff0c;爬虫能够抓取到此静态内容&#xff0c;因此更…...

编程日记 2023/12/11 11:47:24

vue2 cron表达式组件

vue2 cron表达式组件 1. 先上图 2. 代码目录 3. 直接上代码 &#xff08;组件代码太多&#xff0c;直接上压缩包&#xff0c;解压后直接用&#xff0c;压缩包再博客顶部&#xff09; 4. 使用注&#xff1a;示例代码中使用了element-ui // HomeView.vue<template><…...

编程日记 2023/12/11 11:46:23

git-vscode

git-vscode ctrlshiftp 创建分支 create branch 直接切到新的分支了 切换分支 直接点左下角自己选择 vscode中配置仓库 https://blog.csdn.net/zora_55/article/details/129709251 推送tag tag作用就是在 Git 中&#xff0c;标记存储库历史记录中特定提交的一种方式。t…...

编程日记 2023/12/11 11:45:22

Java 语言特性(面试系列1)

一、面向对象编程 1. 封装&#xff08;Encapsulation&#xff09; 定义&#xff1a;将数据&#xff08;属性&#xff09;和操作数据的方法绑定在一起&#xff0c;通过访问控制符&#xff08;private、protected、public&#xff09;隐藏内部实现细节。示例&#xff1a; public …...

编程新知 2025/10/6 4:03:40

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2026/1/28 21:15:38

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2026/2/4 23:47:47

视频字幕质量评估的大规模细粒度基准

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用&#xff0c;因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型&#xff08;VLMs&#xff09;在字幕生成方面…...

编程新知 2026/1/30 14:36:22

2025 后端自学UNIAPP【项目实战：旅游项目】6、我的收藏页面

代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口&#xff08;适配服务端返回 Token&#xff09; export const login async (code, avatar) > {const res await http…...

编程新知 2026/1/29 11:40:13

大模型多显卡多服务器并行计算方法与实践指南

一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术，以解决单机资源不足的问题。分布式训练主要分为两种模式： 数据并行：将数据分片到不同设备，每个设备拥有完整的模型副本 模型并行：将模型分割到不同设备，每个设备处理部分模型计算 现代大模型训练通常结合…...

编程新知 2025/12/10 20:45:02

#Uniapp篇：chrome调试unapp适配

chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器&#xff1a;Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

编程新知 2026/1/4 21:36:42

iview框架主题色的应用

1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题&#xff0c;无需引入&#xff0c;直接可…...

编程新知 2026/1/31 9:29:45

BLEU评分：机器翻译质量评估的黄金标准

BLEU评分&#xff1a;机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域&#xff0c;衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标&#xff0c;自2002年由IBM的Kishore Papineni等人提出以来&#xff0c;…...

编程新知 2026/1/13 7:39:19

uniapp 实现腾讯云IM群文件上传下载功能

UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中&#xff0c;群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS&#xff0c;在uniapp中实现&#xff1a; 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

编程新知 2025/9/14 20:44:53