归并排序与自然归并排序
归并排序
归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并.
核心步骤讲解
归并排序的核心步骤如下:

可以看出,这算法的核心逻辑就是类似小学语文学文章的一种结构的"总-分-总".
让我们来具体剖析一下,来看看它的思路:
拆分过程:以10 6 7 1这一组为例来看一下拆分过程(核心:使用start, end, mid分别表示开头结尾和中间) :

合并过程:让我么以6,10/1,7这一组为例,来看一下合并过程:最主要的地方就在于传入两组要合并的组,然后创建一个新的数组tmpArr,存放要合并的两个组元素,并将tmpArr中的内容放在源数组中对应位置.

下面是代码:
public class MergeSort {public static void mergeSort(int[] arr) {mergeSortFun(arr, 0, arr.length - 1);}public static void mergeSortFun(int[] arr, int start, int end) {//当start和end重合之后,结束递归if(start >= end) {return;}//找到要切割的位置int mid = (start + end) / 2;//左分支mergeSortFun(arr, start, mid);//右分支mergeSortFun(arr, mid + 1, end);//合并内容merge(arr, start, mid, end);}public static void merge(int[] arr, int left, int mid, int right) {//为了好理解,这里重新用s1,s2,e1,e2表示int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;//定义一个新的数组,用来返回排序好的部分int[] tmpArr = new int[right - left + 1];//用k表示下标(在新创建的数组中的位置)int k = 0;while(s1 <= e1 && s2 <= e2) {if(arr[s1] <= arr[s2]) {tmpArr[k++] = arr[s1++];} else {tmpArr[k++] = arr[s2++];}}//用来存放剩余的部分while(s1 <= e1) {tmpArr[k++] = arr[s1++];}while(s2 <= e2) {tmpArr[k++] = arr[s2++];}//将排序好的数组,放到原来的数组中for(int i = 0; i < tmpArr.length; i++) {arr[i + left] = tmpArr[i];}}public static void main(String[] args) {int[] arr = {10, 6, 7, 1, 3, 9, 4, 2};mergeSort(arr);for(int x : arr) {System.out.print(x + " ");}}
}
归并排序总结
1.归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题.
2.时间复杂度:O(N * logN)
3.空间复杂度:O(N)
4.稳定度:稳定.
海量数据的排序问题
外部排序:排序过程中需要在磁盘等外部存储进行的排序.
eg:内存只有1G,需要排序的数据有100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序.而归并排序是最常用的外部排序.
1.先把文件切分成200份,每个512M
2.分别对512M内容进行排序,因为每个内存都放得下,所以任意排序都可以
3.进行二路归并,同时对200份有序文件进行归并过程,最终结果就有序了.
自然归并排序
自然归并排序是归并排序的一种变体,其主要特点是利用输入数据的初始有序性.自然归并排序的思想是先找到已经有序的子序列,然后合并这些子序列,直至整个数组有序.
核心步骤讲解
1.查找有序子序列:从数组的起始位置开始,找到第一个有序子序列(递增或递减).这可以通过遍历数组来实现.
2.合并有序子序列:将找到的有序子序列进行合并,在合并的过程中,继续查找下一个有序子序列,直到整个数组有序.
3.重复步骤1和2:重复执行步骤1和2,直到整个数组完全有序.
以下是大致过程:

相对于之前的归并排序,这里就不是单纯的向下递归的过程,而是一个寻找子序列的过程,而在归并的过程中,是基本与之前的一致的.所以这里只需要分析一下寻找子序列的过程即可:
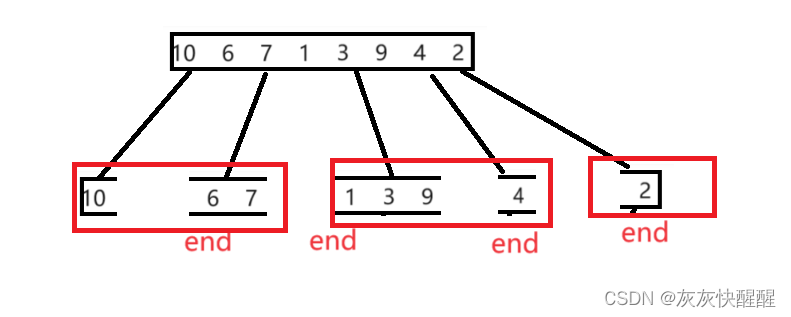
重点:标记的end是上一组的下一个,然后循环时不断标记end,控制为两两一组,进行合并.反复执行上述过程,就可以直接完成.
可能讲的会有点不清楚,请看代码:
import java.util.Arrays;public class NaturalMergeSort {public static void main(String[] args) {int[] array = {10, 6, 7, 1, 3, 9, 4, 2};naturalMergeSort(array);for(int x : array) {System.out.print(x + " ");}}public static void naturalMergeSort(int[] array) {int n = array.length;int[] tempArray = new int[n];int l = -1, m, r;//外部循环,直到不能发现更多的子数组while(l != 0) {l = 0;//内部循环,以寻找并合并有序子数组while (l < n) {m = findNextSortedSubarray(array, l, n, tempArray);//当m 与 n重合时,表明已经找到尾了,退出循环(里和外)if (m == n) {break;}r = findNextSortedSubarray(array, m, n, tempArray);merge(array, l, m, r, tempArray);l = r;}}}//查找下一个有序子数组的方法(返回的是结束位置)private static int findNextSortedSubarray(int[] array, int start, int n, int[] tempArray) {int end = start + 1;while (end < n && array[end - 1] <= array[end]) {end++;}return end;}//二路归并private static void merge(int[] array, int l, int m, int r, int[] tempArray) {int i = l, j = m, k = 0;while (i < m && j < r) {if (array[i] <= array[j]) {tempArray[k++] = array[i++];} else {tempArray[k++] = array[j++];}}while (i < m) {tempArray[k++] = array[i++];}while (j < r) {tempArray[k++] = array[j++];}System.arraycopy(tempArray, 0, array, l, k);}
}
自然归并排序总结
1.这玩意的思路相比于其它排序其实特别恶心,在生产环境中非常不建议使用,你的项目组成员可能会骂街,说你小子装什么逼??(除非是这种情况:就比如你的数据结构老师不知道是为啥心血来潮让你讲这个,整一个反转课堂啥的,那你也没办法~~)
2.时间复杂度:遍历了一次:O(n)
3.空间复杂度:O(n)
相关文章:

归并排序与自然归并排序
归并排序 归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并. 核心步骤讲解 归并排序的…...

22款奔驰GLS450升级HUD抬头显示 告别低头
随着科技飞速地发展,从汽车领域就可以看出,尤其是汽车的抬头显示器,一经推出就吸引了很多的车主。星骏汇小许Xjh15863 升级HUD抬头显示,HUD与汽车系统进行完整的数据信息连接,整合成大数据,然后将一些重要信…...

关于kotlin的属性委托,报错的,实际原因剖析
报错:Property delegate must have a ‘getValue(SecurityCheckView, KProperty*>)’ method. None of the following functions are suitable 解决方案:就是在根目录的build.gradle中改变 kotlin的插件版本 classpath “org.jetbrains.kotlin:kotli…...
HarmonyOS4.0从零开始的开发教程11给您的应用添加弹窗
HarmonyOS(十)给您的应用添加弹窗 概述 在我们日常使用应用的时候,可能会进行一些敏感的操作,比如删除联系人,这时候我们给应用添加弹窗来提示用户是否需要执行该操作,如下图所示: 弹窗是一种…...

js 同步任务和异步任务
同步任务和异步任务 同步任务 同步任务就是没有被引擎挂起、在主线程上排队执行的任务。只有前一个任务执行完,才会执行下一个任务。同步任务具有堵塞效果。 异步任务 异步任务是被引擎放在一边,不进入主线程进入任务队列的任务。只有引擎认为某个异步任…...
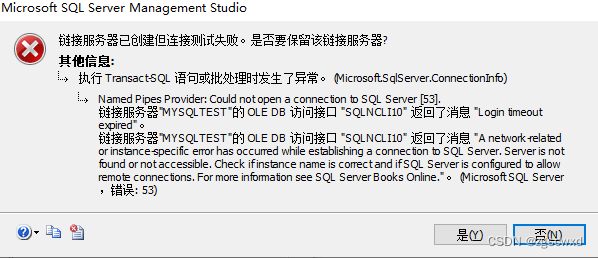
【小白专用】Sql Server 连接Mysql 更新23.12.09
目标 已知mysql连接参数(地址和用户),期望通过Microsoft Sql Server Management Studio (以下简称MSSSMS)连接Mysql,在MSSSMS中直接查询或修改Mysql中的数据。 一般是选最新的版本下载。 选64位还是32位&a…...

DIP——边缘提取与分割
1.使用canny算法进行边缘提取 本实验比较简单,基本思路是对原图像进行一个高斯模糊处理,用于去噪,之后转换为灰度图,直接调用cv库中的canny记性边缘提取。若想直接得到彩色边缘,则通过按位与操作,将原始彩色…...

低代码开发:现实挑战与发展前景
低代码开发是近年来迅速崛起的软件开发方法,让编写应用程序变得更快、更简单。有人说它是美味的膳食,让开发过程高效而满足,但也有人质疑它是垃圾食品,缺乏定制性与深度。 一、什么是低代码 低代码开发是一种基于图形用户界面&…...
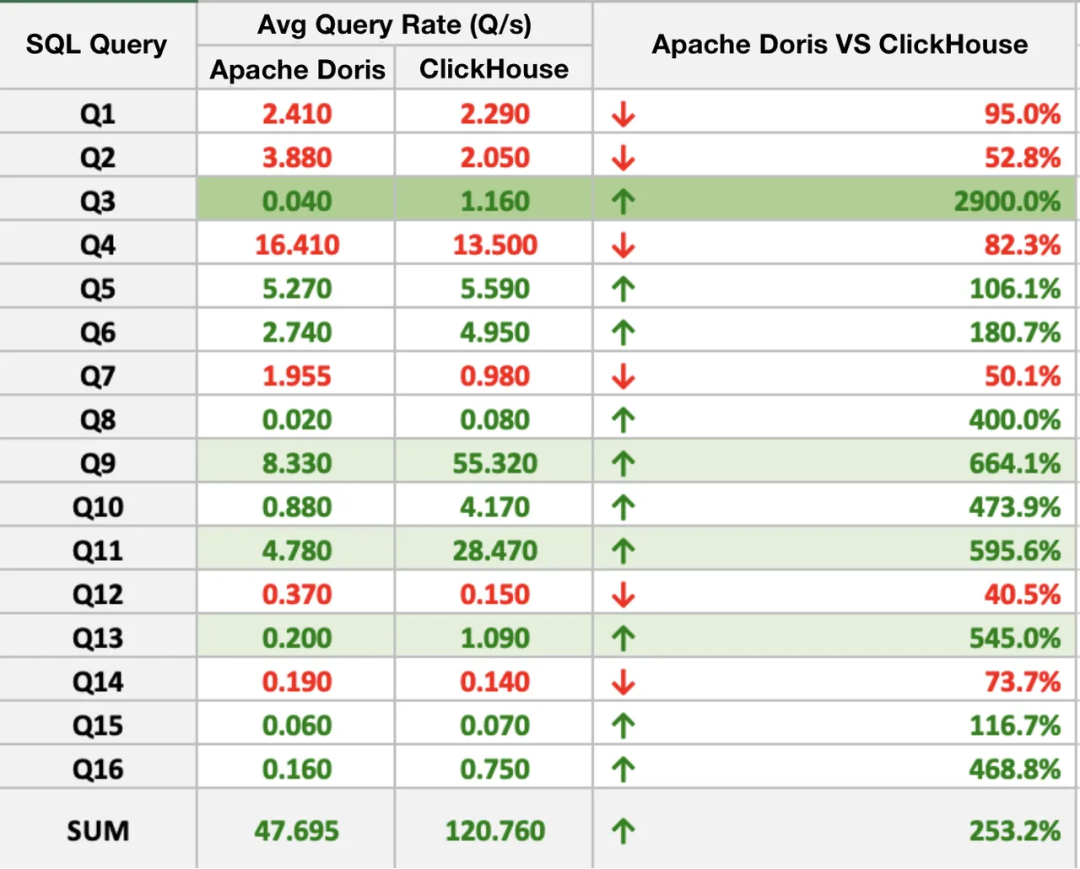
大数据技术7:基于StarRocks统一OALP实时数仓
前言: 大家对StarRocks 的了解可能不及 ClickHouse或者是远不及 ClickHouse 。但是大家可能听说过 Doris ,而 StarRocks 实际上原名叫做 Doris DB ,他相当于是一个加强版的也就是一个 Doris ,也就是说 Doris 所有的功能 StarRocks 都是有的&a…...

C# WPF上位机开发(网络程序界面开发)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 之前我们讨论过,设备之间通讯的方式很多。但是,不知道大家有没有注意,前面谈到的这些通讯方式都需要上位机电脑…...

卡码网语言基础课 | 20. 排队取奶茶
目录 一、 队列的基本认识 二、 队列的操作 2.1 引入头文件 2.2 创建队列 2.3 队列的常见操作 三、 解题 通过本次练习,将会学习到以下C知识点: 队列的基本概念(队头、队尾)和特点(先入先出)入队、出队…...
Angular 进阶之四:SSR 应用场景与局限
应用场景 内容丰富,复杂交互的动态网页,对首屏加载有要求的项目,对 seo 有要求的项目(因为服务端第一次渲染的时候,已经把关键字和标题渲染到响应的 html 中了,爬虫能够抓取到此静态内容,因此更…...
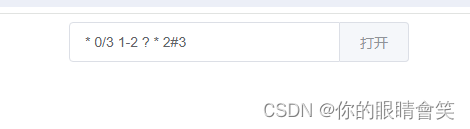
vue2 cron表达式组件
vue2 cron表达式组件 1. 先上图 2. 代码目录 3. 直接上代码 (组件代码太多,直接上压缩包,解压后直接用,压缩包再博客顶部) 4. 使用注:示例代码中使用了element-ui // HomeView.vue<template><…...

git-vscode
git-vscode ctrlshiftp 创建分支 create branch 直接切到新的分支了 切换分支 直接点左下角自己选择 vscode中配置仓库 https://blog.csdn.net/zora_55/article/details/129709251 推送tag tag作用就是在 Git 中,标记存储库历史记录中特定提交的一种方式。t…...
【C++11(三)】智能指针详解--RAII思想循环引用问题
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 C11 1. 前言2. 为什么要有智能指针?3. RAII思想…...
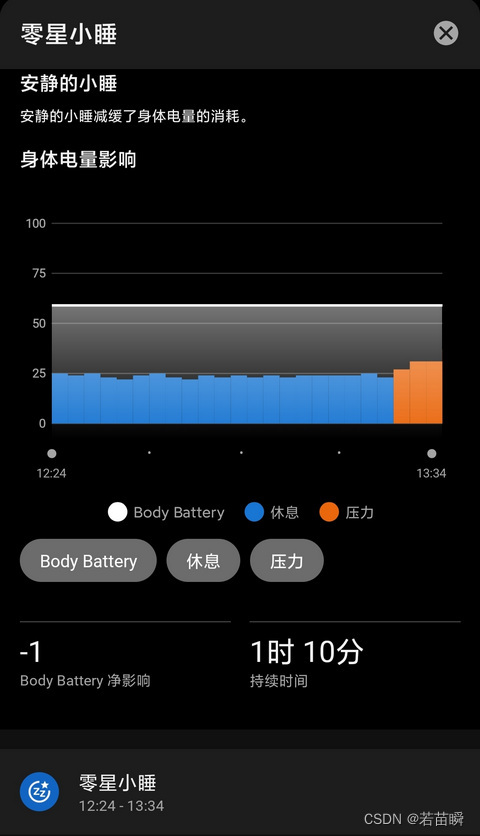
佳明(Garmin) fēnix 7X 增加小睡检测功能
文章目录 (一)零星小睡(二)小睡检测(三)吐槽佳明(3.1)心率检测(3.2)光线感应器(3.3)手表重量(3.4)手表续航 &a…...

二、如何保证架构的质量、架构前期准备、技术填补与崩溃预防、系统重构
1、如何保证架构的质量 -- 稳定性和健壮性 2、正确的选择是良好的开端 -- 架构前期准备 ① 架构师分类:系统架构师、应用架构师、业务架构师 3、技术填补与崩溃预防 4、系统重构...

14、SQL注入——HTTP文件头注入
文章目录 一、HTTP Header概述1.1 HTTP工作原理1.2 HTTP报文类型1.3 较重要的HTTP Header内容 二、HTTP Header注入2.1 HTTP Header注入的前提条件2.2 常见的HTTP Header注入类型 一、HTTP Header概述 1.1 HTTP工作原理 1.2 HTTP报文类型 (1)请求报文 …...
李宏毅bert记录
一、自监督学习(Self-supervised Learning) 在监督学习中,模型的输入为x,若期望输出是y,则在训练的时候需要给模型的期望输出y以判断其误差——有输入和输出标签才能训练监督学习的模型。 自监督学习在没有标注的训练…...

.Net6.0 Microsoft.AspNetCore.Http.Abstractions 2.20 已弃用
您想要升级 Microsoft.AspNetCore.Http.Abstractions 包,您需要注意以下几点: Microsoft.AspNetCore.Http.Abstractions 包在 ASP.NET Core 2.2 版本后已经被标记为过时,因为它已经被包含在 Microsoft.AspNetCore.App 框架引用中12。因此&am…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
