【算法系列篇】递归、搜索和回溯(二)

文章目录
- 前言
- 1. 两两交换链表中的节点
- 1.1 题目要求
- 1.2 做题思路
- 1.3 代码实现
- 2. Pow(X,N)
- 2.1 题目要求
- 2.2 做题思路
- 2.3 代码实现
- 3. 计算布尔二叉树的值
- 3.1 题目要求
- 3.2 做题思路
- 3.3 代码实现
- 4. 求根节点到叶结点数字之和
- 4.1 题目要求
- 4.2 做题思路
- 4.3 代码实现
前言
前面为大家介绍了关于递归的知识,以及使用递归解决了几个问题,那么这篇文章将带大家巩固一下关于递归的知识。
1. 两两交换链表中的节点
https://leetcode.cn/problems/swap-nodes-in-pairs/description/
1.1 题目要求
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
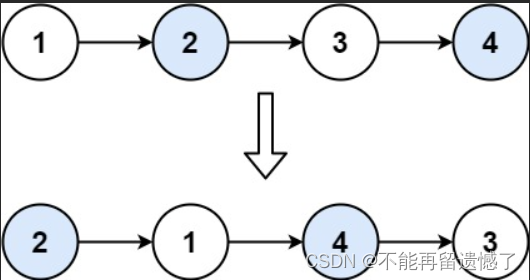
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {}
}
1.2 做题思路
这道题目其实可以使用非递归的方式来实现,但是我们可以使用递归的方式来加深一下递归的学习。
这个题目不复杂,比较简单,我们可以将 head 和 head.next 看成一部分,另外的节点看成另一部分,开始我们直接将后面部分的节点交给函数处理,相信它一定可以帮助我们完成两两节点的交换,当后面部分的节点交换完成之后,我们再交换 head 和 head.next 节点,然后再将这两个部分连接起来。
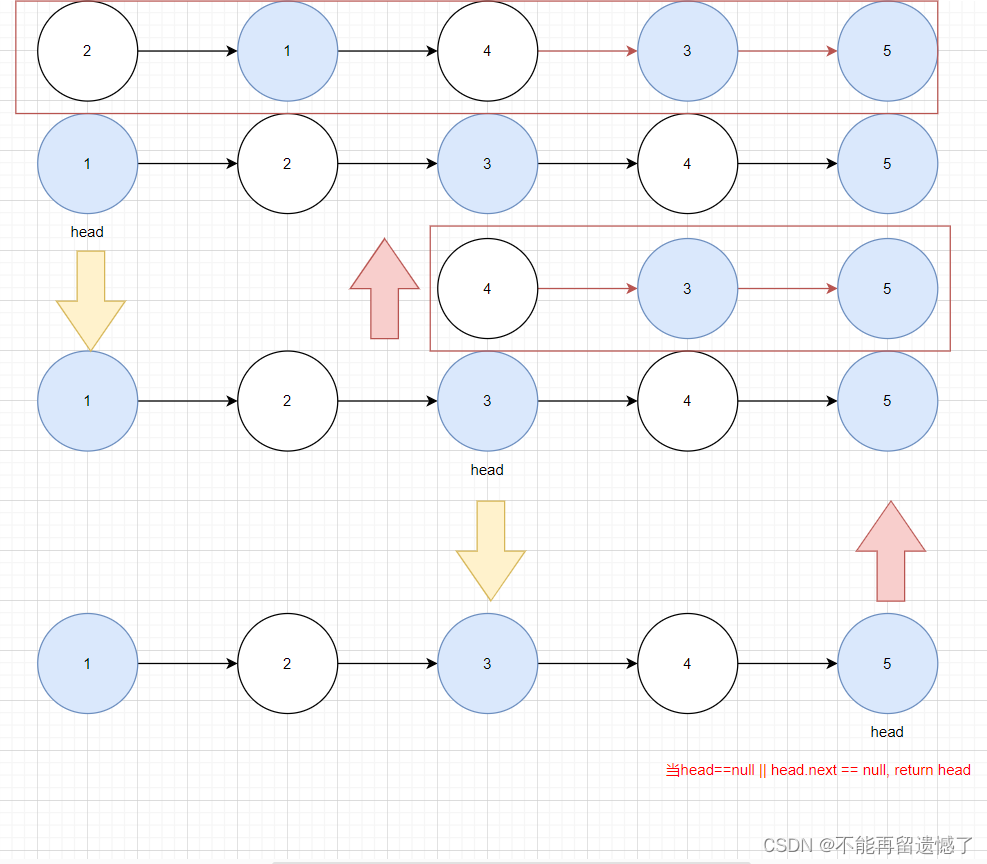
这是一种思路,我们也可以先交换前面部分,然后再交换后面部分。
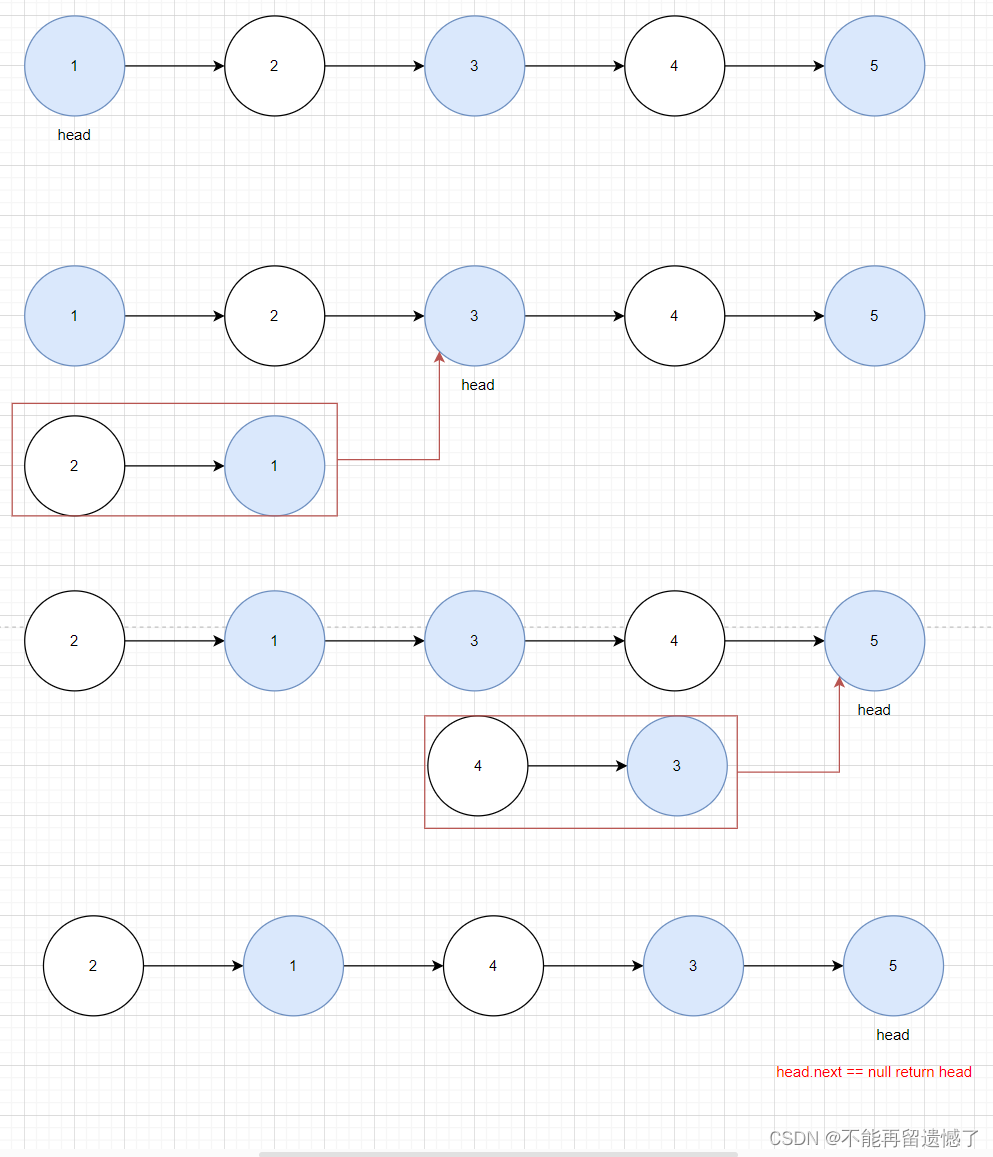
上面两种思路其实都差不多的,只是先交换还是后交换的区别。
1.3 代码实现
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) return head;ListNode l1 = swapPairs(head.next.next);ListNode ret = head.next;head.next.next = head;head.next = l1;return ret;}
}
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) return head;ListNode curNext = head.next.next;ListNode ret = head.next;head.next.next = head;head.next = swapPairs(curNext);return ret;}
}
2. Pow(X,N)
https://leetcode.cn/problems/powx-n/
2.1 题目要求
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一个整数
要么 x 不为零,要么 n > 0 。
-104 <= xn <= 104
class Solution {public double myPow(double x, int n) {}
}
2.2 做题思路
其实这道题也叫做快速幂,为什么叫做快速幂呢?给大家举个例子:假设我们要求2^8,普通的做法就是2x2x2x2x2x2x2x2,但是呢?2 ^ 8可以写成 2 ^ 4 x 2 ^ 4,而 2 ^ 4 又可以写成 2 ^ 2 x 2 ^ 2,2 ^ 2可以写成 2 x 2,2 可以写成 1 x 2。也就是说 2 ^ n 可以写成 2 ^ (n / 2) x 2 ^ (n / 2),我们每次只需要计算 2 ^ (n / 2) 的值及,就可以了,通过这种快速幂的方法,就可以大大节省计算的时间。
当幂为偶数的话就可以每次求 x 的 n / 2 次幂,但是如果幂数为奇数该怎么办呢?这也不复杂,当幂数为奇数的时候,我们只需要在 n / 2 次幂 x n / 2 次幂后面在乘上一个 x 就可以了。举个例子:2 ^ 5就可以写成 2 ^ 2 x 2 ^ 2 x 2。
2.3 代码实现
class Solution {public double myPow(double x, int n) {//处理幂数的正负问题if (n < 0) return 1.0 / quickPow(x, n);else return quickPow(x, n);}private double quickPow(double x, int n) {if (n == 0) return 1.0;double t = quickPow(x, n / 2);//处理幂数的奇偶问题return n % 2 == 0 ? t * t : t * t * x;}
}
3. 计算布尔二叉树的值
https://leetcode.cn/problems/evaluate-boolean-binary-tree/
3.1 题目要求
给你一棵 完整二叉树 的根,这棵树有以下特征:
叶子节点 要么值为 0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。
非叶子节点 要么值为 2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND
计算 一个节点的值方式如下:
如果节点是个叶子节点,那么节点的 值 为它本身,即 True 或者 False 。
否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:
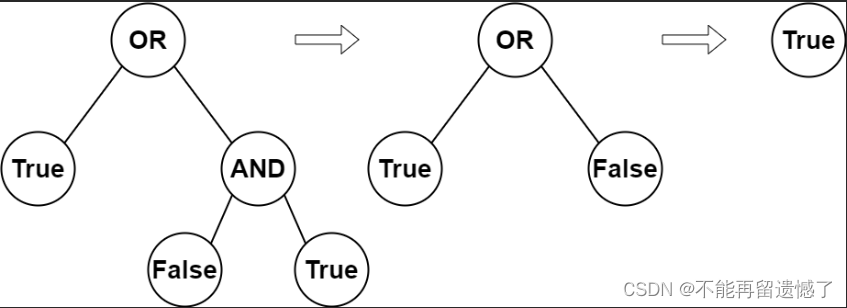
输入:root = [2,1,3,null,null,0,1]
输出:true
解释:上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。
示例 2:
输入:root = [0]
输出:false
解释:根节点是叶子节点,且值为 false,所以我们返回 false 。
提示:
树中节点数目在 [1, 1000] 之间。
0 <= Node.val <= 3
每个节点的孩子数为 0 或 2 。
叶子节点的值为 0 或 1 。
非叶子节点的值为 2 或 3 。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {}
}
3.2 做题思路
这道题目的意思就是如果遇到的节点是一个叶子节点的话,如果当前节点的值为0的话就返回False,为1的话就返回True;如果当前节点不是叶子节点的话,就需要根据这个节点的父亲节点的值与这个节点的兄弟节点进行操作,如果父亲节点是2的话,就进行 | 操作,3就进行 & 操作。
一般遇到二叉树就会想到递归,这道题也不例外。我们先将根节点的左树交给函数,让函数帮助我们进行布尔值的计算,然后再将根节点的右树交给函数进行布尔值的运算,最后将左右子树的值与根节点表示的值进行 | 或者 & 运算。
3.3 代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {//当root为null时返回trueif (root == null) return true;//遇到叶子节点根据节点的值返回if (root.left == null && root.right == null) {if (root.val == 0) return false;else return true;}boolean l = evaluateTree(root.left);boolean r = evaluateTree(root.right);if (root.val == 2) return l | r;else return l & r;}
}
4. 求根节点到叶结点数字之和
https://leetcode.cn/problems/sum-root-to-leaf-numbers/
4.1 题目要求
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
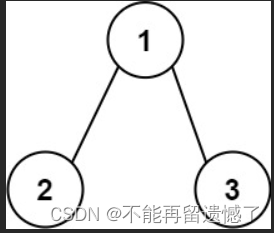
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
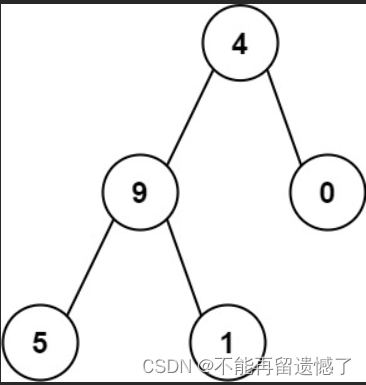
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumNumbers(TreeNode root) {}
}
4.2 做题思路
这道题目也不难,只要能理解二叉树的的前序遍历就可以了,这道题目其实就是二叉树的前序遍历。我们先将根节点的左子树交给函数得到左子树上从根节点到各个叶子节点路径上的数字之和,然后将根节点的右子树上的从根节点到各个叶子节点路径上的数字之和,然后返回左子树和右子树返回值的和。
4.3 代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumNumbers(TreeNode root) {return dfs(root, 0);}//n用来记录当前路径上该节点之前的各个节点的和private int dfs(TreeNode root, int n) {if (root == null) return 0;//遇到一个节点就将当前节点的值加在n上n = n * 10 + root.val;//遇到叶子节点就说明当前节点的值计算完成,就返回路径上所以数字和if (root.left == null && root.right == null) return n;//分别计算根节点左右子树上根节点到叶子节点路径上数字和int l = dfs(root.left, n);int r = dfs(root.right, n);//返回左子树和右子树所有路径上数字和return l + r;}
}
相关文章:

【算法系列篇】递归、搜索和回溯(二)
文章目录 前言1. 两两交换链表中的节点1.1 题目要求1.2 做题思路1.3 代码实现 2. Pow(X,N)2.1 题目要求2.2 做题思路2.3 代码实现 3. 计算布尔二叉树的值3.1 题目要求3.2 做题思路3.3 代码实现 4. 求根节点到叶结点数字之和4.1 题目要求4.2 做题思路4.3 代码实现 前言 前面为大…...

Ubuntu下安装SDL
源码下载地址(SDL version 2.0.14):https://www.libsdl.org/release/SDL2-2.0.14.tar.gz 将源码包拷贝到系统里 使用命令解压 tar -zxvf SDL2-2.0.14.tar.gz 解压得到文件夹 SDL2-2.0.14 进入文件夹 执行命令 ./configure 执行命令 make…...

创建vue项目:vue脚手架安装、vue-cli安装,vue ui界面创建vue工程(vue2/vue3),安装vue、搭建vue项目开发环境(保姆级教程二)
今天讲解 Windows 如何利用脚手架创建 vue 工程,以及 vue ui 图形化界面搭建 vue 开发环境,这是这个系列的第二章,有什么问题请留言,请点赞收藏!!! 文章目录 1、安装vue-cli脚手架2、vue ui创建…...
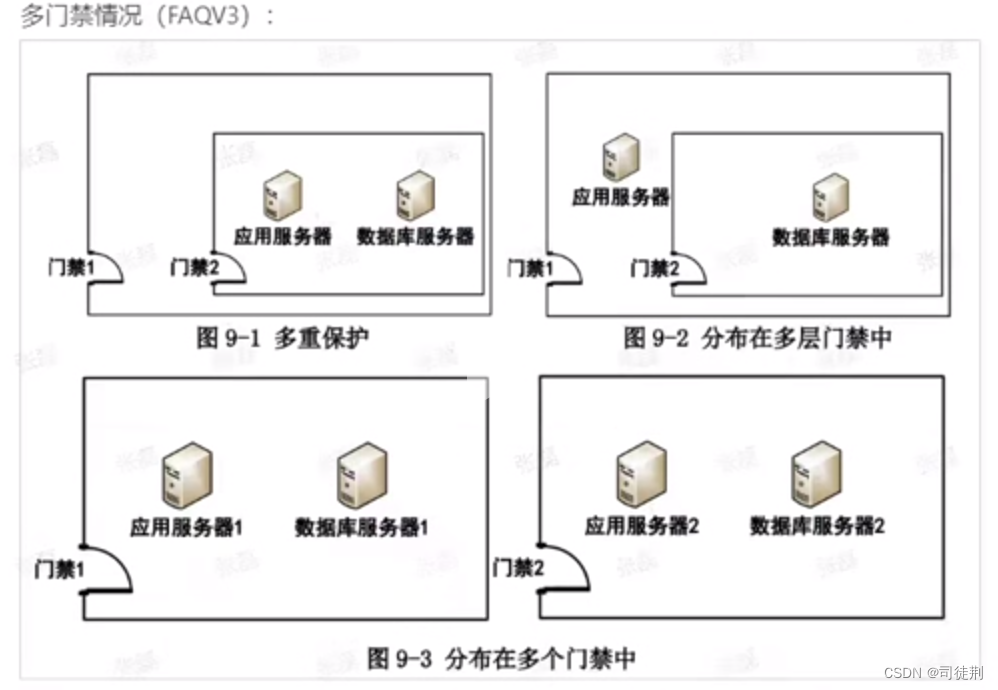
【3】密评-物理和环境安全测评
0x01 依据 GB/T 39786 -2021《信息安全技术 信息系统密码应用基本要求》针对等保三级系统要求: 物理和环境层面: a)宜采用密码技术进行物理访问身份鉴别,保证重要区域进入人员身份的真实性; b)宜采用密码技术保证电子门…...

笨爸爸工房,我们在校园|“小鲁班”,铸未来
为了响应国家号召,将劳动教育课程真正实现融入校园生活,笨爸爸工房已与洛阳市西下池小学、洛阳市第一实验小学西工校区、洛阳市西工区第二实验小学、洛阳第二外国语学校(兰溪校区)、洛阳市睿源幼儿园,这4所学校及1家幼…...

RPC 集群,gRPC 广播和组播
一、集群抽象:cluster 它是指我们在调用远程的时候,尝试解决: 1、failover:即引入重试功能,但是重试的时候会换一个新节点 2、failfast: 立刻失败,不需要重试 3、广播:将请求发送到所有的节点上 4、组…...
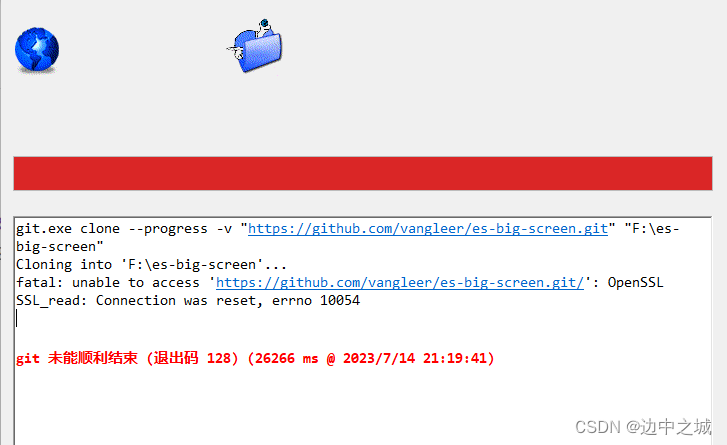
OpenSSL SSL_read: Connection was reset, errno 10054
fatal: unable to access ‘https://github.com/vangleer/es-big-screen.git/’: OpenSSL SSL_read: Connection was reset, errno 10054 解决方法:git config --global http.sslVerify “false” 参考链接: https://github.com/Kong/insomnia/issues/2…...
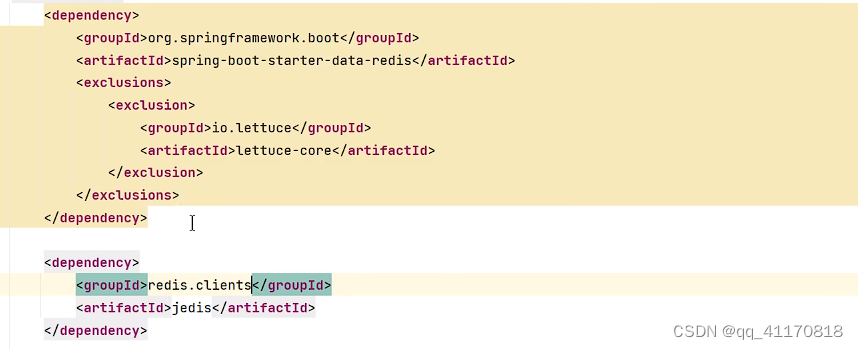
【springboot】整合redis和定制化
1.前提条件:docker安装好了redis,确定redis可以访问 可选软件: 2.测试代码 (1)redis依赖 org.springframework.boot spring-boot-starter-data-redis (2)配置redis (3) 注入 Resource StringRedisTemplate stringRedisTemplate; 这里如果用Autowi…...

HarmonyOS鸿蒙操作系统架构开发
什么是HarmonyOS鸿蒙操作系统? HarmonyOS是华为公司开发的一种全场景分布式操作系统。它可以在各种智能设备(如手机、电视、汽车、智能穿戴设备等)上运行,具有高效、安全、低延迟等优势。 目录 HarmonyOS 一、HarmonyOS 与其他操…...
共创共赢|美创科技获江苏移动2023DICT生态合作“产品共创奖”
12月6日,以“5G江山蓝 算网融百业 数智创未来”为主题的中国移动江苏公司2023DICT合作伙伴大会在南京成功举办。来自行业领军企业、科研院所等DICT产业核心力量的百余家单位代表参加本次大会,共话数实融合新趋势,共拓合作发展新空间。 作为生…...
)
深度学习——第3章 Python程序设计语言(3.5 Python类和对象)
3.5 Python类和对象 目录 1. 面向对象的基本概念 2. 类和对象的关系 3. 类的声明 4. 对象的创建和使用 5. 类对象属性 6. 类对象方法 7. 面向对象的三个基本特征 8. 综合案例:汉诺塔图形化移动 1.1 面向对象的基本概念 1.1.1 对象(object&#x…...

【原创】【一类问题的通法】【真题+李6卷6+李4卷4(+李6卷5)分析】合同矩阵A B有PTAP=B,求可逆阵P的策略
【铺垫】二次型做的变换与相应二次型矩阵的对应:二次型f(x1,x2,x3)xTAx,g(y1,y2,y3)yTBy ①若f在可逆变换xPy下化为g,即P为可逆阵,有P…...

代码随想录算法训练营第六十天 | 84.柱状图中最大的矩形
84.柱状图中最大的矩形 题目链接:84. 柱状图中最大的矩形 本题与接雨水相近。按列来看,是要找到每一个柱子左右第一个比它矮的柱子,即对于该柱子来说所能组成的最大面积,将每个柱子所能得到的最大面积进行对比最终得到最大矩形。 …...
C#结合JavaScript实现多文件上传
目录 需求 引入 关键代码 操作界面 JavaScript包程序 服务端 ashx 程序 服务端上传后处理程序 小结 需求 在许多应用场景里,多文件上传是一项比较实用的功能。实际应用中,多文件上传可以考虑如下需求: 1、对上传文件的类型、大小…...
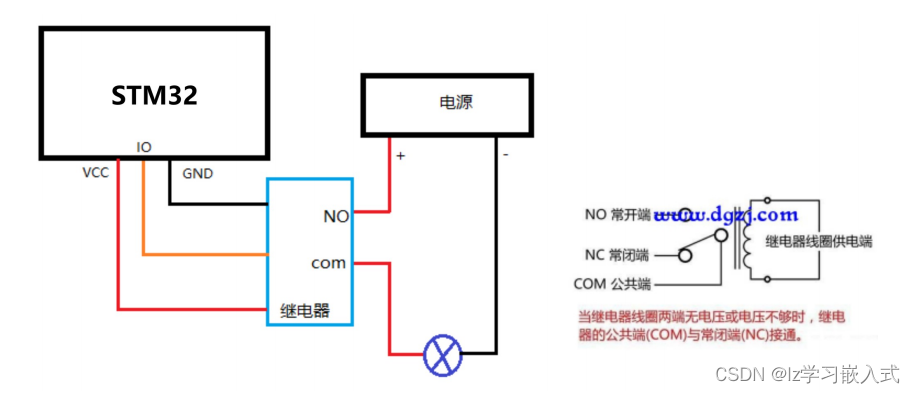
STM32——继电器
继电器工作原理 单片机供电 VCC GND 接单片机, VCC 需要接 3.3V , 5V 不行! 最大负载电路交流 250V/10A ,直流 30V/10A 引脚 IN 接收到 低电平 时,开关闭合。...
性能监控体系:InfluxDB Grafana Prometheus
InfluxDB 简介 什么是 InfluxDB ? InfluxDB 是一个由 InfluxData 开发的,开源的时序型数据库。它由 Go 语言写成,着力于高性能地查询与存储时序型数据。 InfluxDB 被广泛应用于存储系统的监控数据、IoT 行业的实时数据等场景。 可配合 Te…...

CS106L2023 and CS106B 环境配置(详细教程)
1.问题: (1)CS106L 运行./setup.sh 脚本时出错 (windows 请下载git,在git bash 打开运行) (2)CS106B,QT构建 构建错误:一般构建错误,例如 Erro…...
Docker-多容器应用
一、概述 到目前为止,你一直在使用单个容器应用。但是,现在您将 MySQL 添加到 应用程序堆栈。经常会出现以下问题 - “MySQL将在哪里运行?将其安装在同一个 容器还是单独运行?一般来说,每个容器都应该做一件事&#x…...
Golang导入导出Excel表格
最近项目开发中有涉及到Excel的导入与导出功能,特别是导出表格时需要特定的格式(单元格合并等),废话不多说,直接上代码了。 首先用到一个第三方库,实测还是很强大很好用的,就是这个https://git…...

基于Maven的Spring Boot应用版本号获取解析
引言 在Spring Boot应用的开发和部署中,了解应用的版本号对于管理和监控应用至关重要。本文将深入解析一种基于Maven打包的Spring Boot应用中,根据不同的运行环境获取应用版本号的解决方案。在开始介绍代码之前,我们先来了解一下可能的文件目…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
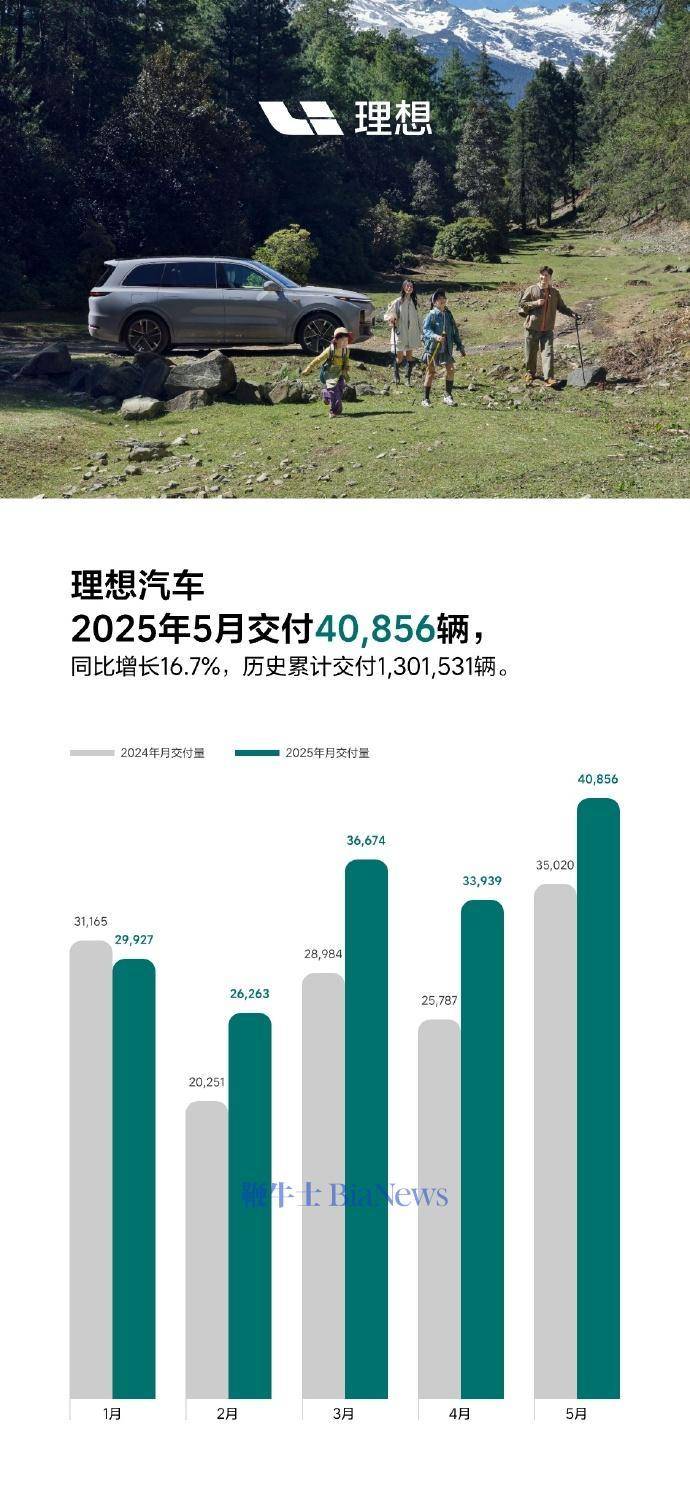
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
