【原创】【一类问题的通法】【真题+李6卷6+李4卷4(+李6卷5)分析】合同矩阵A B有PTAP=B,求可逆阵P的策略
【铺垫】二次型做的变换与相应二次型矩阵的对应:二次型f(x1,x2,x3)=xTAx,g(y1,y2,y3)=yTBy
①若f在可逆变换x=Py下化为g,即P为可逆阵,有PTAP=B;此时P来源于二次型f g代数配方的系数阵。A B合同
②若f在正交变换x=Qy下化为g,即Q为正交阵,有QTAP=Q^(-1)AQ=B;此时Q来源于矩阵方法求A,B的特征值特征向量,产生的过渡正交阵Q,使得QTAQ=B。A B合同且相似
·故若让求合同矩阵A B的可逆过渡阵P,使PTAP=B,P的构成来源可以是:A B对应二次型代数配方的可逆系数阵(此时二次型做可逆变换),或者A B化为对角阵的正交阵(此时二次型做正交变换)
【思考】若实对称阵A B合同但不相似,且有可逆阵Q使得QTAQ=B,那么Q可能为正交阵吗?
【回答】Q不可能为正交阵。因为若Q为正交阵,则Q(-1)=QT,则有Q(-1)AQ=B,此时A B相似,与条件矛盾

【问题引入】若实对称阵A B合同,考虑A B均非对角阵的一般情况,则有可逆阵P,使得PTAP=B,求P的策略(不考虑成对初等变换)
【分析】合同矩阵A B有相同的规范型,总存在对角阵∧和可逆阵C D,使得CTAC=∧=DTBD
若A B合同但不相似,C D中最多有1个正交阵〔不可能 C D 均为正交阵〕【但若A B不仅合同且相似,则C D可能均为正交阵,一般可逆阵也可。例如C D均为正交阵,24李6卷5线代大题:二次型f(xi)在正交变换x=Qy变换下化为二次型g(yi),让求Q;记f g对应二次型矩阵为A B,则有正交阵Q使得QTAQ=B,A B相似。将A B分别用一个正交阵Q1 Q2对角化(此不用配方),根据Q1 Q2即可得Q。下面说A B合同但不相似的情况】
【核心思想】①写A B对应的二次型f(xi),g(yi)
②选用代数配方法或正交矩阵法,将A B在可逆阵C D的作用下化为同一个对角阵∧,即CTAC=∧=DTBD(C D中可能存在最多一个正交阵)。后可根据C D求出PTAP=B的可逆阵P
·其实基本默认可优先考虑配方法,若给过铺垫可考虑一下正交阵。注意若A B合同但不相似,最终PTAP=B的P不可能为正交阵(见上提问),正交阵只可能与另一个可逆阵相乘构成P
【情况一】C D中无正交阵〔20数二大题+24李6数二第6套大题〕
【实操】①A用相应二次型f(xi)配方(即可逆变换x=Cz)到对角阵∧〔C为配方系数阵的逆〕
②B用相应二次型g(yi)配方(即可逆变换y=Dz)到同一个∧〔D为配方系数阵的逆〕
【注】(1)化为的同一个∧通常为f g共同的规范型
(2)20数二线代大题要自己将f g同时配方为同一规范型;24李4数二线代第一问已让求出了f到规范型的可逆变换x=Cy〔即已找到C使CTAC=∧=E〕。而A B都是正定阵,规范型均为E;第2问再求出g到规范型的可逆变换y=Dz〔即再求出D使DTBD=∧=E〕;结合C D即可求出PTAP=B的P
【情况二】若C D中有正交阵,设C为正交阵,D为可逆阵〔24李4数二第4套大题考法〕
【实操】①将A用正交阵C化到标准型∧,即CTAC=∧〔相应二次型f(xi)做正交变换x=Cz〕
②B用相应二次型g(yi)配方(即可逆变换y=Dz)到同一个∧〔D为配方系数阵的逆〕
【注】(1)f g化为的同一个∧通常为正交阵C的标准型
(2)24李4数二第4套线代大题套路,就是第一问让用正交变化x=Qy求出了f的标准型〔即求出了正交阵Q使QTAQ=∧1=diag(a+1,a+1,a-2),∧1则为A的标准型〕;第二问记B=(A-aE)²,注意到一问的Q也可使QTBQ=∧2=diag(1,1,4),此时再将B做可逆变换y=Dz配方到∧3=E〔即易写出可逆阵D,使DT∧2D=∧3=E(因为∧2原本就是对角阵了)〕。故有DTQTBQD(=∧3)=E,而让求PTBP=E,可取P=QD。本题虽形式上设问略有不同,但手法思想类似
(3)【注意】C D中有无正交阵其实可以“自定义”,如当下面情况可出现正交阵
①第一问让求过正交阵C,使CTAC=∧〔24李4数二第4套考法〕;则此时只需对B相应二次型g(yi)配方即可
②配方难配或矩阵AorB的特征值易求
相关文章:

【原创】【一类问题的通法】【真题+李6卷6+李4卷4(+李6卷5)分析】合同矩阵A B有PTAP=B,求可逆阵P的策略
【铺垫】二次型做的变换与相应二次型矩阵的对应:二次型f(x1,x2,x3)xTAx,g(y1,y2,y3)yTBy ①若f在可逆变换xPy下化为g,即P为可逆阵,有P…...

代码随想录算法训练营第六十天 | 84.柱状图中最大的矩形
84.柱状图中最大的矩形 题目链接:84. 柱状图中最大的矩形 本题与接雨水相近。按列来看,是要找到每一个柱子左右第一个比它矮的柱子,即对于该柱子来说所能组成的最大面积,将每个柱子所能得到的最大面积进行对比最终得到最大矩形。 …...
C#结合JavaScript实现多文件上传
目录 需求 引入 关键代码 操作界面 JavaScript包程序 服务端 ashx 程序 服务端上传后处理程序 小结 需求 在许多应用场景里,多文件上传是一项比较实用的功能。实际应用中,多文件上传可以考虑如下需求: 1、对上传文件的类型、大小…...
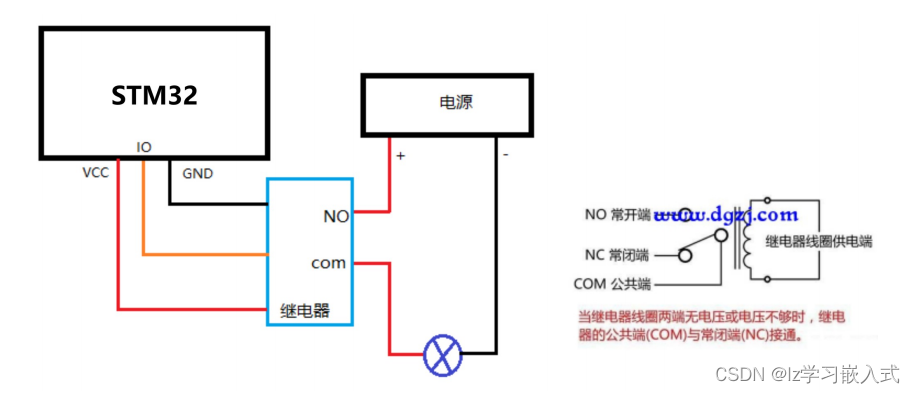
STM32——继电器
继电器工作原理 单片机供电 VCC GND 接单片机, VCC 需要接 3.3V , 5V 不行! 最大负载电路交流 250V/10A ,直流 30V/10A 引脚 IN 接收到 低电平 时,开关闭合。...
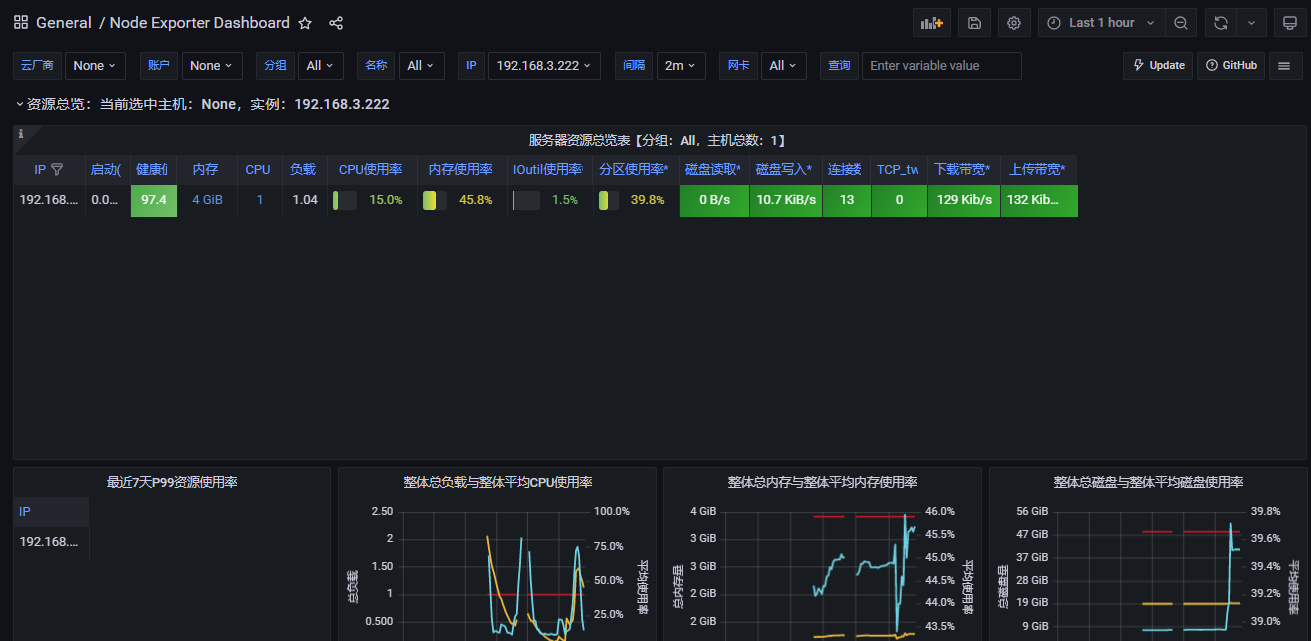
性能监控体系:InfluxDB Grafana Prometheus
InfluxDB 简介 什么是 InfluxDB ? InfluxDB 是一个由 InfluxData 开发的,开源的时序型数据库。它由 Go 语言写成,着力于高性能地查询与存储时序型数据。 InfluxDB 被广泛应用于存储系统的监控数据、IoT 行业的实时数据等场景。 可配合 Te…...

CS106L2023 and CS106B 环境配置(详细教程)
1.问题: (1)CS106L 运行./setup.sh 脚本时出错 (windows 请下载git,在git bash 打开运行) (2)CS106B,QT构建 构建错误:一般构建错误,例如 Erro…...
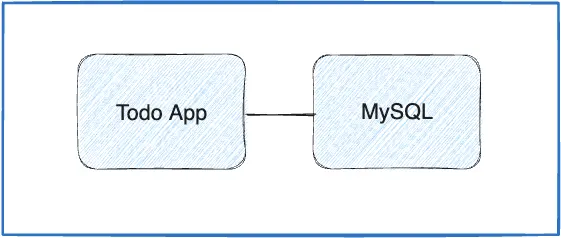
Docker-多容器应用
一、概述 到目前为止,你一直在使用单个容器应用。但是,现在您将 MySQL 添加到 应用程序堆栈。经常会出现以下问题 - “MySQL将在哪里运行?将其安装在同一个 容器还是单独运行?一般来说,每个容器都应该做一件事&#x…...
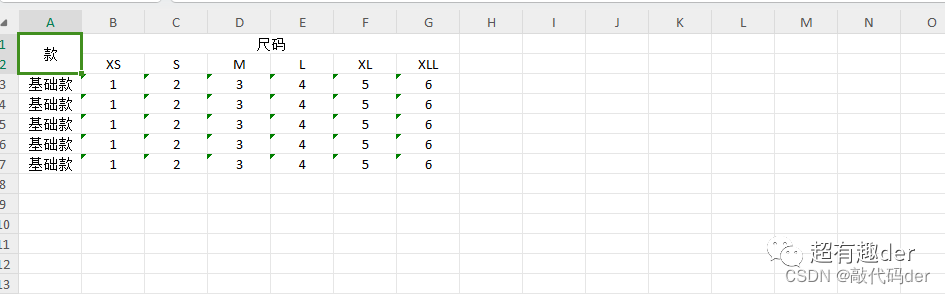
Golang导入导出Excel表格
最近项目开发中有涉及到Excel的导入与导出功能,特别是导出表格时需要特定的格式(单元格合并等),废话不多说,直接上代码了。 首先用到一个第三方库,实测还是很强大很好用的,就是这个https://git…...

基于Maven的Spring Boot应用版本号获取解析
引言 在Spring Boot应用的开发和部署中,了解应用的版本号对于管理和监控应用至关重要。本文将深入解析一种基于Maven打包的Spring Boot应用中,根据不同的运行环境获取应用版本号的解决方案。在开始介绍代码之前,我们先来了解一下可能的文件目…...
| 微调LLAMA-2和其他开源LLM的两种简单方法)
LLM微调(二)| 微调LLAMA-2和其他开源LLM的两种简单方法
本文将介绍两种开源工具来微调LLAMA-2。 一、使用autotrain-advanced微调LLAMA-2 AutoTrain是一种无代码工具,用于为自然语言处理(NLP)任务、计算机视觉(CV)任务、语音任务甚至表格任务训练最先进的模型。 1…...
的需求规范)
AVP对纵向控制ESP(Ibooster)的需求规范
目录 1. 版本记录... 3 2. 文档范围和控制... 4 2.1 目的/范围... 4 2.2 文档冲突... 4 2.3 文档授权... 4 2.4 文档更改控制... 4 3. 功能概述... 5 4. 系统架构... 6 5. 主要安全目标... 7 5.1 …...
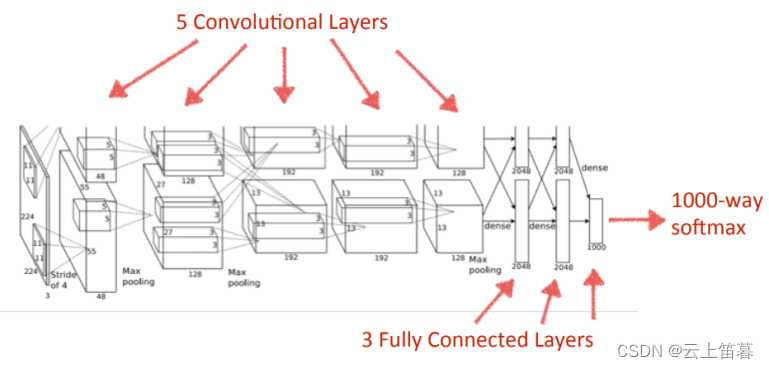
小模型学习(1)-人脸识别
【写作背景】因为最近一直在研究大模型,在与客户进行交流时,如果要将大模型的变革性能力讲清楚,就一定要能将AI小模型的一些原理和效果讲清楚,进而形成对比。当然这不是一件简单的事情,一方面大模型分析问题的的本质原…...
sublime Text使用
1、增加install 命令面板 工具(tool)->控制面板(command palette) -> 输入install ->安装第一个install package controller,以下安装过了,所以没展示 2、安装json格式化工具 点击install package,等几秒会进入控制面板࿰…...

基于深度学习的yolov7植物病虫害识别及防治系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介简介YOLOv7 系统特性工作流程 二、功能三、系统四. 总结 一项目简介 # YOLOv7植物病虫害识别及防治系统介绍 简介 该系统基于深度学习技术,采…...

Leetcode 2963. Count the Number of Good Partitions
Leetcode 2963. Count the Number of Good Partitions 1. 解题思路2. 代码实现 题目链接:2963. Count the Number of Good Partitions 1. 解题思路 这一题根据题意,显然我们可以将其先分为 n n n个原子partition,确保任意两个partition之间…...

C语言动态内存经典笔试题分析
C语言动态内存经典笔试题分析 文章目录 C语言动态内存经典笔试题分析1. 题目一2. 题目二3. 题目三4. 题目四 1. 题目一 void GetMemory(char *p){p (char *)malloc(100);} void Test(void){char *str NULL;GetMemory(str);strcpy(str, "hello world");printf(str)…...
X.rvs(10000))
截断正态分布stats.truncnorm()X.rvs(10000)
就是在均值和方差之外,再指定正态分布随机数群的上下限,如 [ μ − 3 σ , μ 3 σ ] [\mu-3\sigma,\mu3\sigma] [μ−3σ,μ3σ] stats.truncnorm()参数 X stats.truncnorm(-2, 2, locmu, scalesigma) -2 2是截断的正态分布…...
)
第59天:django学习(八)
事务 事务是MySQL数据库中得一个重要概念,事务的目的:为了保证多个SQL语句执行成功,执行失败,前后保持一致,保证数据安全。 开启事务的三个关键字 start transaction commit rollback 开启事务 from django.db import transaction…...
技术。)
举例说明自然语言处理(NLP)技术。
本文章由AI生成! 以下是自然语言处理(NLP)技术的一些例子: 机器翻译:将一种语言翻译成另一种语言的自动化过程。常见的机器翻译系统包括谷歌翻译,百度翻译等。 语音识别:将口头语言转换成文本…...

echarts地图marker自定义图标并添加点击事件
symbol如果引用https图片链接会报403,直接引用本地 series: [{type: scatter, // 使用散点图系列 coordinateSystem: geo, // 设置坐标系为地理坐标系 zlevel: 100,data: [{name: 上海,value: [121.48, 31.22], // 上海的经纬度坐标 symbol: image:// require(/…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
