截断正态分布stats.truncnorm()X.rvs(10000)
就是在均值和方差之外,再指定正态分布随机数群的上下限,如 [ μ − 3 σ , μ + 3 σ ] [\mu-3\sigma,\mu+3\sigma] [μ−3σ,μ+3σ]
stats.truncnorm()参数
X = stats.truncnorm(-2, 2, loc=mu, scale=sigma)
-2 2是截断的正态分布的方差倍数大小,loc是均值,scale是方差 这个的截断的大小是 [ μ − 2 σ , μ + 2 σ ] [\mu-2\sigma,\mu+2\sigma] [μ−2σ,μ+2σ]
import matplotlib.pyplot as plt
import scipy.stats as stats
import pylab
from pylab import *mu, sigma = 5, 0.7
lower, upper = mu - 2 * sigma, mu + 2 * sigma # 截断在[μ-2σ, μ+2σ]
X = stats.truncnorm(-2, 2, loc=mu, scale=sigma)
N = stats.norm(loc=mu, scale=sigma)figure(1)
subplot(2, 1, 1)
plt.hist(X.rvs(10000)) # 截断正态分布的直方图
subplot(2, 1, 2)
plt.hist(N.rvs(10000)) # 常规正态分布的直方图
plt.show()
这个代码中的X.rvs(10000)是说在X中随机选取10000个数据
相关文章:
X.rvs(10000))
截断正态分布stats.truncnorm()X.rvs(10000)
就是在均值和方差之外,再指定正态分布随机数群的上下限,如 [ μ − 3 σ , μ 3 σ ] [\mu-3\sigma,\mu3\sigma] [μ−3σ,μ3σ] stats.truncnorm()参数 X stats.truncnorm(-2, 2, locmu, scalesigma) -2 2是截断的正态分布…...
)
第59天:django学习(八)
事务 事务是MySQL数据库中得一个重要概念,事务的目的:为了保证多个SQL语句执行成功,执行失败,前后保持一致,保证数据安全。 开启事务的三个关键字 start transaction commit rollback 开启事务 from django.db import transaction…...
技术。)
举例说明自然语言处理(NLP)技术。
本文章由AI生成! 以下是自然语言处理(NLP)技术的一些例子: 机器翻译:将一种语言翻译成另一种语言的自动化过程。常见的机器翻译系统包括谷歌翻译,百度翻译等。 语音识别:将口头语言转换成文本…...

echarts地图marker自定义图标并添加点击事件
symbol如果引用https图片链接会报403,直接引用本地 series: [{type: scatter, // 使用散点图系列 coordinateSystem: geo, // 设置坐标系为地理坐标系 zlevel: 100,data: [{name: 上海,value: [121.48, 31.22], // 上海的经纬度坐标 symbol: image:// require(/…...

C盘瘦身,C盘清理
以下只是我的C盘清理经验~ 一.【用软件简单清理C盘】 使用一些垃圾清理软件,简单的初步把C盘先清理一遍。(这种软件太多我就不推荐了……) 二.【WPS清理大师】 因为我电脑装了WPS,发现右键单击C盘有个选项【释放C盘空间】…...
STM32F103
提示:来源正点原子,参考STM32F103 战舰开发指南V1.3PDF资料 文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 提示:这里可以添加本文要记录的大概内容: 开发环境硬件普中科技,接…...

Unity使用打成图集的Sprite作为模型贴图使用的问题
大家好,我是阿赵。 有时候用Unity引擎做项目的时候,会遇到这样的需求,美术做了一些模型或者特效,然后策划想在游戏运行的时候,读取一些游戏图标放在特效或者模型上面当做贴图使用。 这个需求实现起来很简单&am…...

el-select赋值对象是对象时,出现赋值与展示不一致问题
代码逻辑类似:module 是个object { "appId": "", "id": 65, "name": "" } <el-form :model"form"><el-form-item label"申请模块" ><el-select v-model"…...

在 Node-RED 中引入 ECharts 实现数据可视化
Node-RED 提供了强大的可视化工具,而通过引入 ECharts 图表库,您可以更直观地呈现和分析数据。在这篇博客中,我们将介绍两种在 Node-RED 中实现数据可视化的方法:一种是引入本地 ECharts 库,另一种是直接使用 CDN&…...
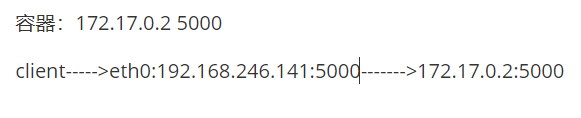
docker资源限制
目录 系统压力测试工具stress 1. cpu资源限制 1.1 限制CPU Share 1.2 限制CPU 核数 1.3 CPU 绑定 2. mem资源限制 3. 限制IO 二、端口转发 三、容器卷 四、部署centos7容器应用 五、docker数据存储位置 六、docker网络 容器网络分类 在使用 docker 运行容器时&…...
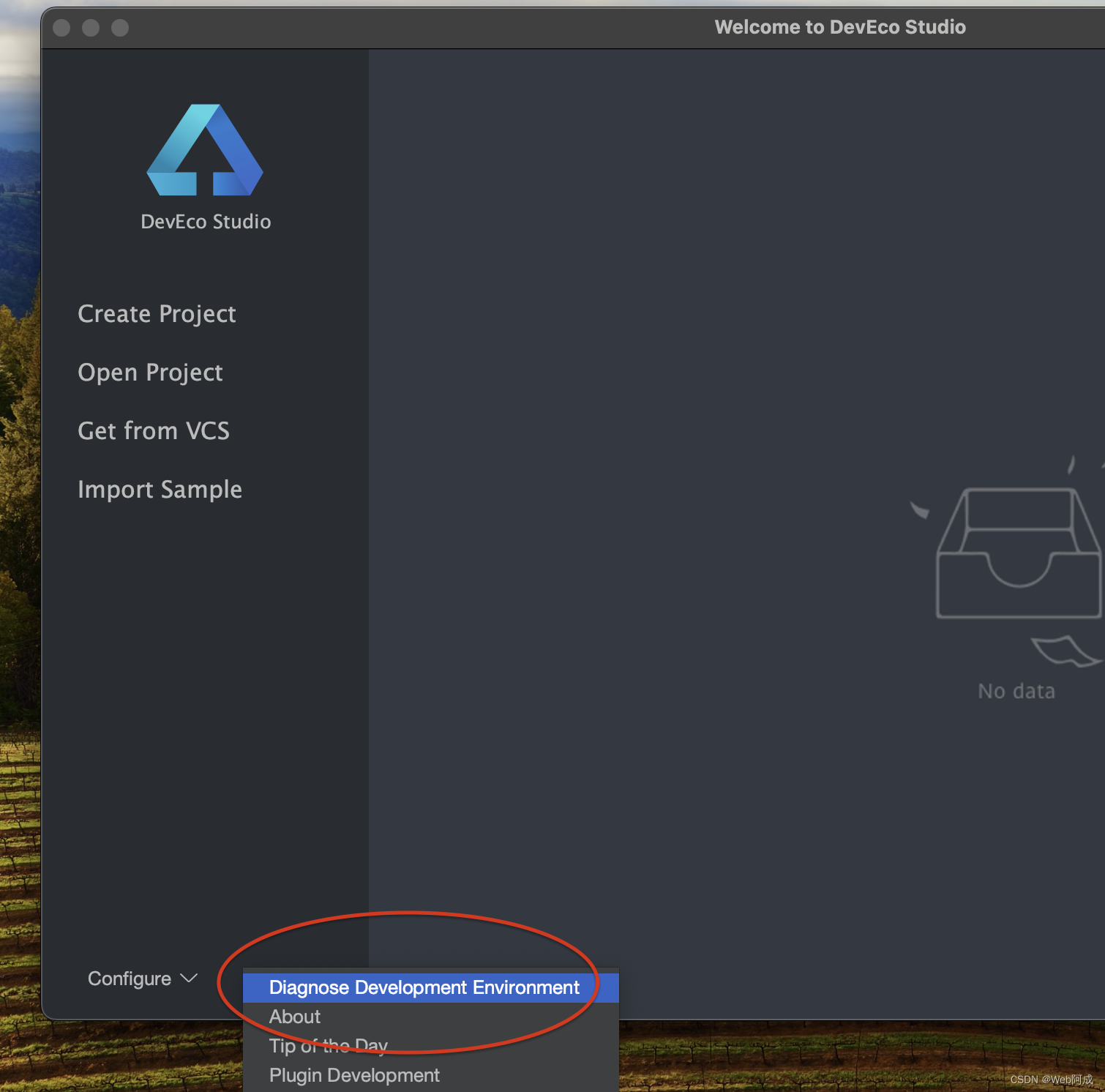
探索HarmonyOS_开发软件安装
随着华为推出HarmonyOS NEXT 宣布将要全面启用鸿蒙原声应用,不在兼容安卓应用, 现在开始探索鸿蒙原生应用的开发。 HarmonyOS应用开发官网 - 华为HarmonyOS打造全场景新服务 鸿蒙官网 开发软件肯定要从这里下载 第一个为微软系统(windows),第…...

CSS中控制元素水平布局的七个属性
元素的水平方向的布局 元素在其父元素中水平方向的位置由一下几个属性共同决定 margin-left border-left padding-left width padding-right border-right margin-right 一个元素在其父元素中,水平布局必须要满足以下…...

YOLOv8改进 | 2023检测头篇 | 利用AFPN改进检测头适配YOLOv8版(全网独家创新)
一、本文介绍 本文给大家带来的改进机制是利用今年新推出的AFPN(渐近特征金字塔网络)来优化检测头,AFPN的核心思想是通过引入一种渐近的特征融合策略,将底层、高层和顶层的特征逐渐整合到目标检测过程中。这种渐近融合方式有助于…...

测试经理的职责是什么?
测试经理的职责是什么? 从项目启动到项目结束的管理 测试计划 获得客户对交付产品的认可 批准中间可交付内容并向客户发布补丁 记录工作内容以便绩效考评或其他计费 问题管理 团队管理 向测试协调员或SQA提交每周状态报告 参加每周回顾会议 每周发布所有测试项目的…...
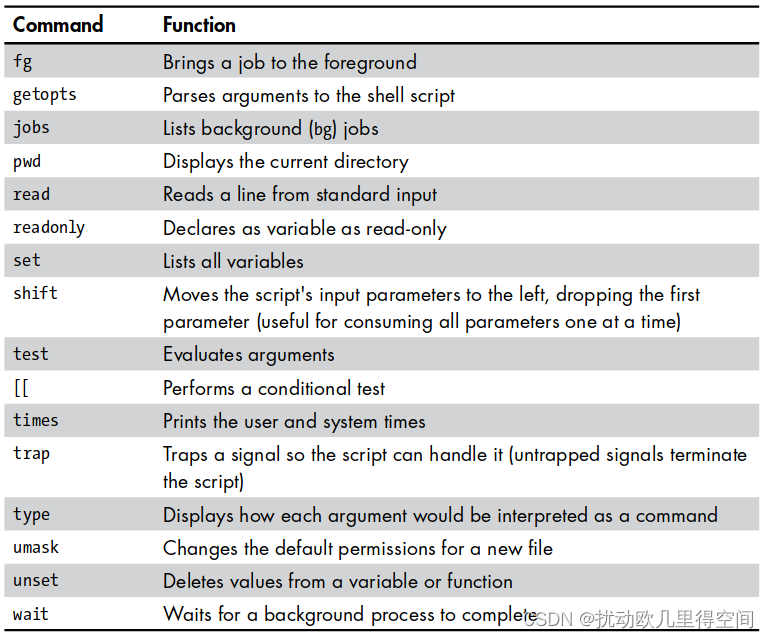
LinuxBasicsForHackers笔记 -- BASH 脚本
你的第一个脚本:“你好,黑客崛起!” 首先,您需要告诉操作系统您要为脚本使用哪个解释器。 为此,请输入 shebang,它是井号和感叹号的组合,如下所示:#! 然后,在 shebang …...
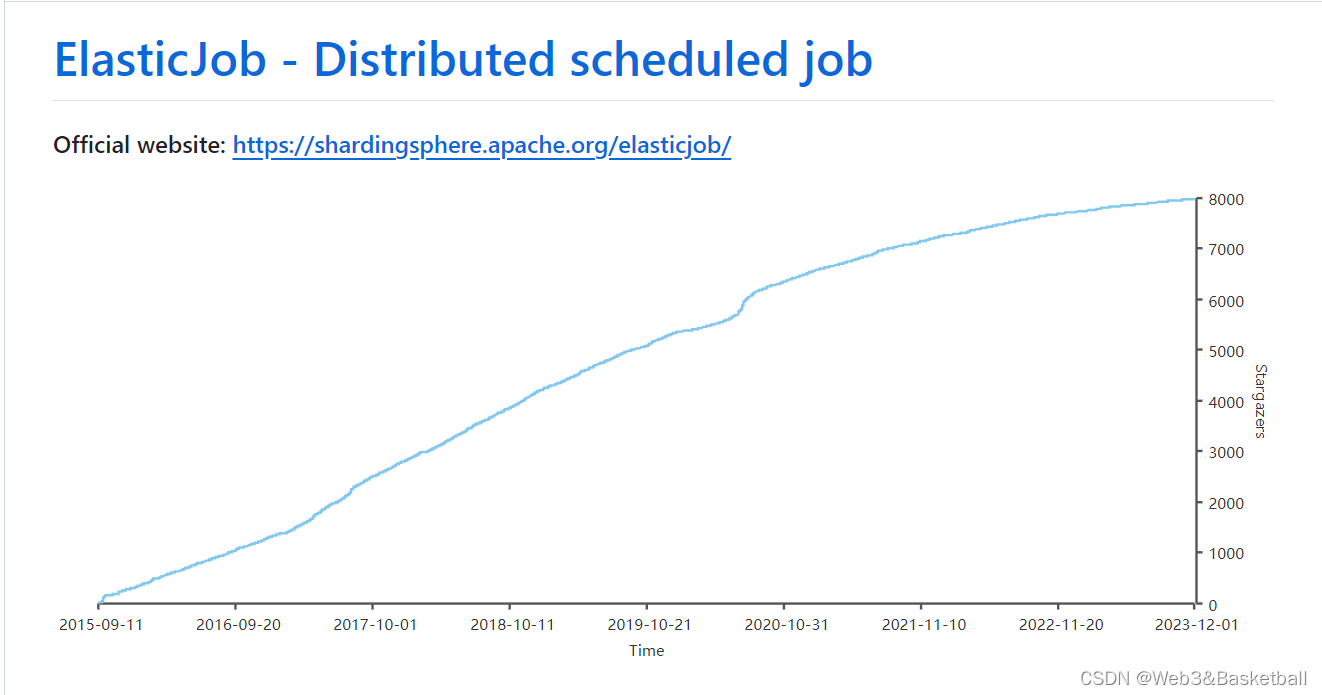
定时任务特辑 | Quartz、xxl-job、elastic-job、Cron四个定时任务框架对比,和Spring Boot集成实战
专栏集锦,大佬们可以收藏以备不时之需: Spring Cloud 专栏:http://t.csdnimg.cn/WDmJ9 Python 专栏:http://t.csdnimg.cn/hMwPR Redis 专栏:http://t.csdnimg.cn/Qq0Xc TensorFlow 专栏:http://t.csdni…...

【面试经典150 | 二叉树】对称二叉树
文章目录 写在前面Tag题目来源解题思路方法一:递归方法二:迭代 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的…...

使用Git进行版本控制
参考:《Python编程从入门到实践》 前言1、安装、配置 Git1.1 在Linux系统中安装Git1.2 在OS X系统中安装Git1.3 在Windows系统中安装Git1.4 配置Git 2、创建项目3、忽略文件4、初始化仓库5、检查状态6、将文件加入到仓库中7、执行提交8、查看提交历史 前言 版本控制…...

专业课145+总分440+东南大学920考研专业基础综合信号与系统数字电路经验分享
个人情况简介 今年考研440,专业课145,数一140,期间一年努力辛苦付出,就不多表了,考研之路虽然艰难,付出很多,当收获的时候,都是值得,考研还是非常公平,希望大…...

Leetcode每日一题
https://leetcode.cn/problems/binary-tree-preorder-traversal/ 这道题目需要我们自行进行创建一个数组,题目也给出我们需要自己malloc一个数组来存放,这样能达到我们遍历的效果,我们来看看他的接口函数给的是什么。 可以看到的是这个接口函…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
