【面试经典150 | 二叉树】对称二叉树
文章目录
- 写在前面
- Tag
- 题目来源
- 解题思路
- 方法一:递归
- 方法二:迭代
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【递归】【迭代】【二叉树】
题目来源
101. 对称二叉树

解题思路
如果一棵树的左子树与右子树镜像对称,那么这两棵树是对称的。
因此,问题转换为:两棵树在什么情况下是互为镜像的,找出使两棵树互为镜像的条件,根据条件即可结局对称问题。
镜像条件如下:
- 两棵树的两个根节点具有相同的值;
- 每棵树的右子树都要与另一棵树的左子树镜像对称。
同时满足以上两个条件即可判断出两棵树是对称的。
二叉树问题通常都有两种递归和迭代的解法。
方法一:递归
递归出口是什么?
递归出口即可以直接判断的情况,包括:
- 两个节点都为空时,直接返回
true; - 一个节点为空,另一个不为空,返回
false。
如何往下递?
当前的两个节点表示的子树是否是对称的,取决于当前两节点的值以及左右子树是否对称。
只有当前两节点的值相等并且左右子树对称,这两个节点表示的子树才是对称的。
算法
实现一个判断两个节点 p 和 q 表示的子树是否是对称的函数 check:
- 如果
p = nullptr并且q = nullptr,直接返回true; - 如果
p ≠ nullptr或者q ≠ nullptr,直接返回false; - 最后
p和q表示的子树是否是对称与p->val == q->val && check(p->left, q->right) && check(p->right, q->left)一致,直接返回该表达式。
调用 check(root, root) 即得到最终答案。
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为二叉树中节点的数量。
空间复杂度: O ( n ) O(n) O(n)。
方法二:迭代
思路与算法
使用迭代解法需要用到队列。
首先我们引入一个队列,初始化时我们把根节点入队两次。每次提取两个节点并比较它们的值(队列中每两个连续的节点应该是相等的,而且它们的子树互为镜像),然后将两个节点的左右子节点按相反的顺序插入队列中。
当队列为空时,或者我们检测到树不对称,即从队列中取出两个不相等的连续节点时,该算法结束。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool check(TreeNode* u, TreeNode *v) {queue<TreeNode*> q;q.push(u); q.push(v);while (!q.empty()) {u = q.front(); q.pop();v = q.front(); q.pop();if (!u && !v)continue;if (!u || !v ||(u->val != v->val))return false;q.push(u->left);q.push(v->right);q.push(u->right);q.push(v->left);}return true;}bool isSymmetric(TreeNode* root) {return check(root, root);}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为二叉树中节点的数量。
空间复杂度: O ( n ) O(n) O(n),因为二叉树中的节点最多入队、出队一次,因此渐进的时间复杂度为 O ( n ) O(n) O(n)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 二叉树】对称二叉树
文章目录 写在前面Tag题目来源解题思路方法一:递归方法二:迭代 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的…...

使用Git进行版本控制
参考:《Python编程从入门到实践》 前言1、安装、配置 Git1.1 在Linux系统中安装Git1.2 在OS X系统中安装Git1.3 在Windows系统中安装Git1.4 配置Git 2、创建项目3、忽略文件4、初始化仓库5、检查状态6、将文件加入到仓库中7、执行提交8、查看提交历史 前言 版本控制…...

专业课145+总分440+东南大学920考研专业基础综合信号与系统数字电路经验分享
个人情况简介 今年考研440,专业课145,数一140,期间一年努力辛苦付出,就不多表了,考研之路虽然艰难,付出很多,当收获的时候,都是值得,考研还是非常公平,希望大…...

Leetcode每日一题
https://leetcode.cn/problems/binary-tree-preorder-traversal/ 这道题目需要我们自行进行创建一个数组,题目也给出我们需要自己malloc一个数组来存放,这样能达到我们遍历的效果,我们来看看他的接口函数给的是什么。 可以看到的是这个接口函…...

USB连接器
USB连接器 电子元器件百科 文章目录 USB连接器前言一、USB连接器是什么二、USB连接器的类别三、USB连接器的应用实例四、USB连接器的作用原理总结前言 USB连接器的使用广泛,几乎所有现代电子设备都具备USB接口,使得设备之间的数据传输和充电变得简单和便捷。 一、USB连接器是…...
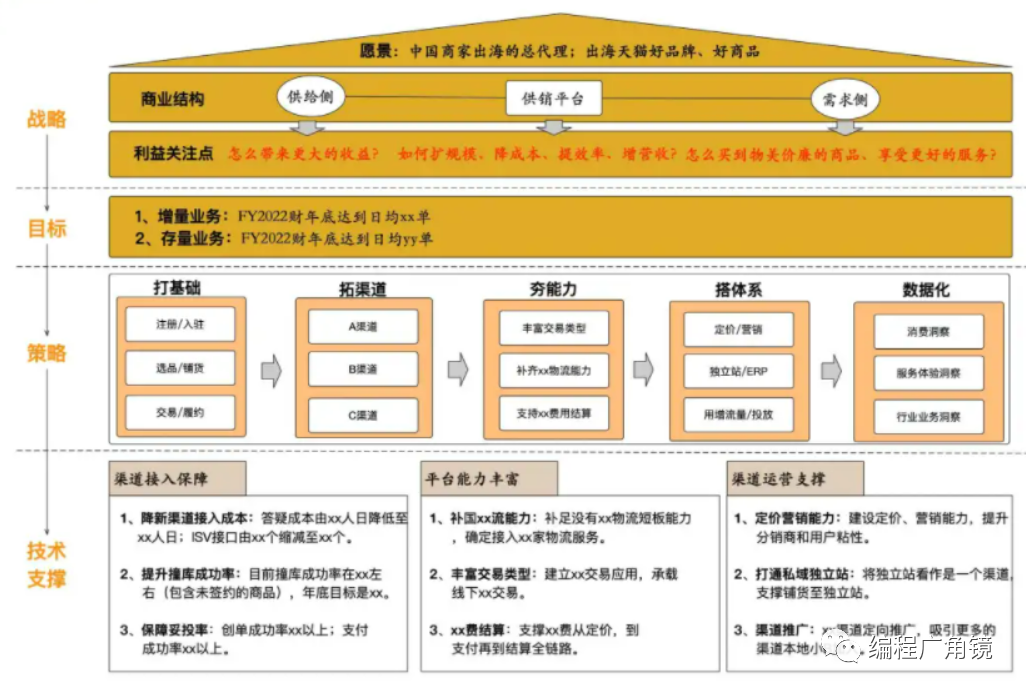
软件工程之需求分析
一、对需求的基本认识 1.需求分析简介 (1)什么是需求 用户需求:由用户提出。原始的用户需求通常是不能直接做成产品的,需要对其进行分析提炼,最终形成产品需求。 产品需求:产品经理针对用户需求提出的解决方案。 (2)为什么要…...
URL提示不安全
当用户访问一个没有经过SSL证书加密的网站(即使用HTTP而不是HTTPS协议),或者SSL证书存在问题时,浏览器URL会显示不安全提示。这些提示旨在保护用户免受潜在的恶意活动,并提醒他们谨慎对待这些不安全的网站。那么该如何…...

JavaBean是什么
详情请参考JavaBean规范:https://www.oracle.com/java/technologies/javase/javabeans-spec.html JavaBean是可重用的软件组件,是一个java类,方法名称符合一定的规范,这样使用方使用起来方便,例如框架和工具可以根据规…...

202309-2
http://118.190.20.162/view.page?gpidT174 题目分析: 这道题读完题后感觉像是考察前缀和,这里回顾下什么是前缀和:https://blog.csdn.net/weixin_45629285/article/details/111146240 我们利用前缀和算法,就可以在O(nm)的时…...
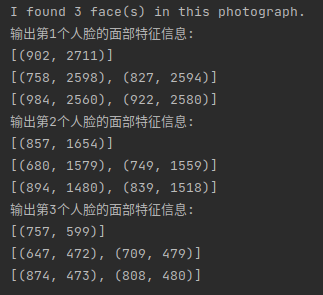
数字图像处理(实践篇)二十 人脸特征提取
目录 1 安装face_recognition 2 涉及的函数 3 实践 使用face_recognition进行人脸特征提取. 1 安装face_recognition pip install face_recognition 或者 pip --default-timeout100 install face_recognition -i http://pypi.douban.com/simple --trusted-host pypi.dou…...
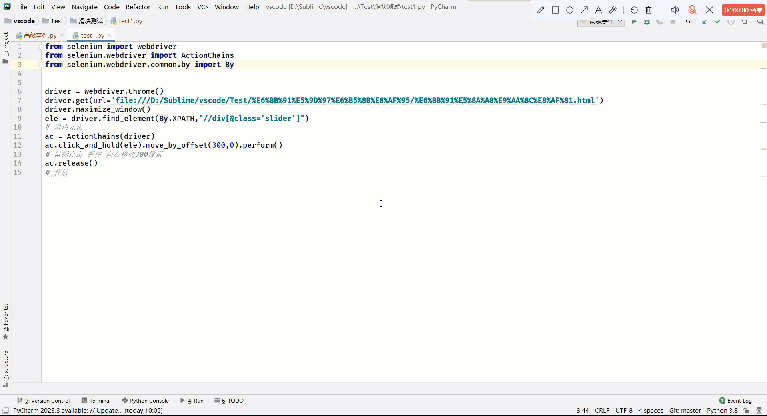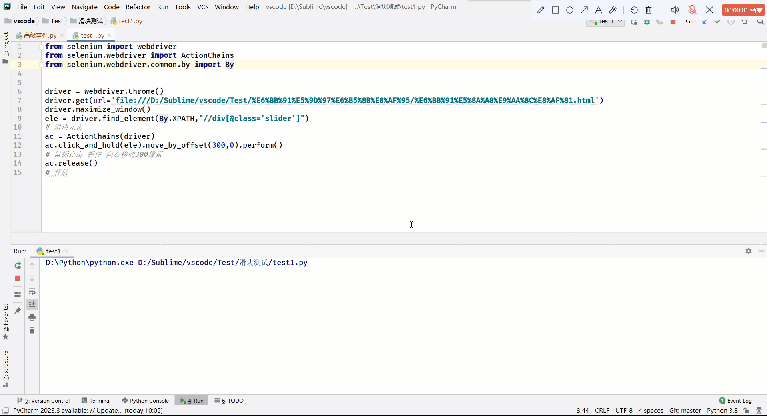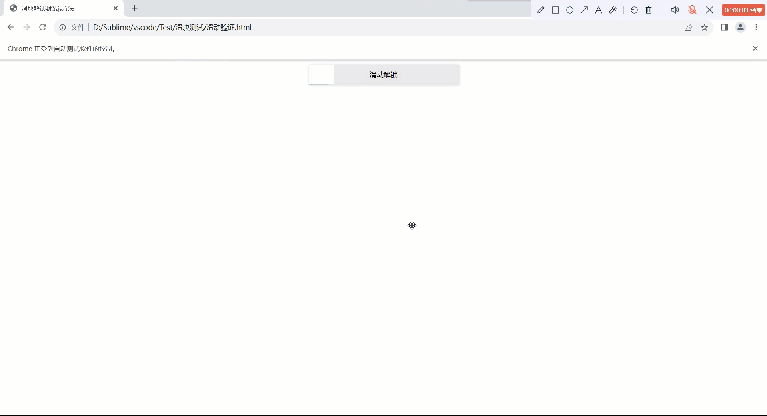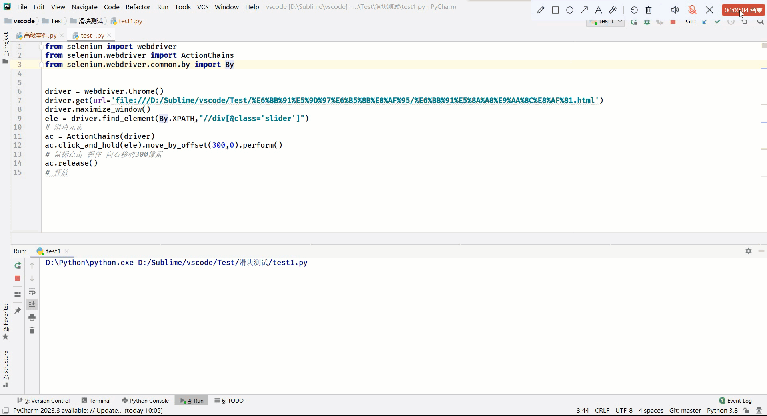
Python自动化:selenium常用方法总结
使用的Python版本为3.8,selenium版本为4.15.2 Python自动化:selenium常用方法总结 1. 三种等待方式2. 浏览器操作3. 8种查找元素的方法4. 高级事件 1. 三种等待方式 强制等待 使用模块time下的sleep()实现等待效果隐式等待 使用driver.implicitly_wait()方法&#…...
『开源资讯』JimuReport积木报表 v1.6.6 版本发布—免费报表工具
项目介绍 一款免费的数据可视化报表,含报表和大屏设计,像搭建积木一样在线设计报表!功能涵盖,数据报表、打印设计、图表报表、大屏设计等! Web 版报表设计器,类似于excel操作风格,通过拖拽完成报…...

每天五分钟计算机视觉:使用1*1卷积层来改变输入层的通道数量
本文重点 在卷积神经网络中有很多重要的卷积核,比如1*1的卷积核,3*3的卷积核,本文将讲解1*1的卷积核的使用,它在卷积神经网络中具有重要的地位。由于1*1的卷积核使用了最小的窗口,那么1*1的卷积核就失去了卷积层可以识…...

Java (JDK 21) 调用 OpenCV (4.8.0)
Java 调用 OpenCV 一.OpenCV 下载和安装二.创建 Java Maven 项目三.其他测试 一.OpenCV 下载和安装 Open CV 官网 可以下载编译好的包,也可以下载源码自行编译 双击安装 opencv-4.8.0-windows.exe 默认为当前目录 安装即解压缩 根据系统位数选择 将 x64 目录下 op…...

git 常用的使用方法
1.查看分支 $ git branch #查看本地分支 $ git branch -r #查看远程分支 $ git branch -a #查看所有分支 $ git branch -vv #查看本地分支及追踪的分支 2.创建分支 方法1 $ git branch 分支名 #创建本地分支 #将本地分支push,就创建了远程分支方法2 #创建本地分…...
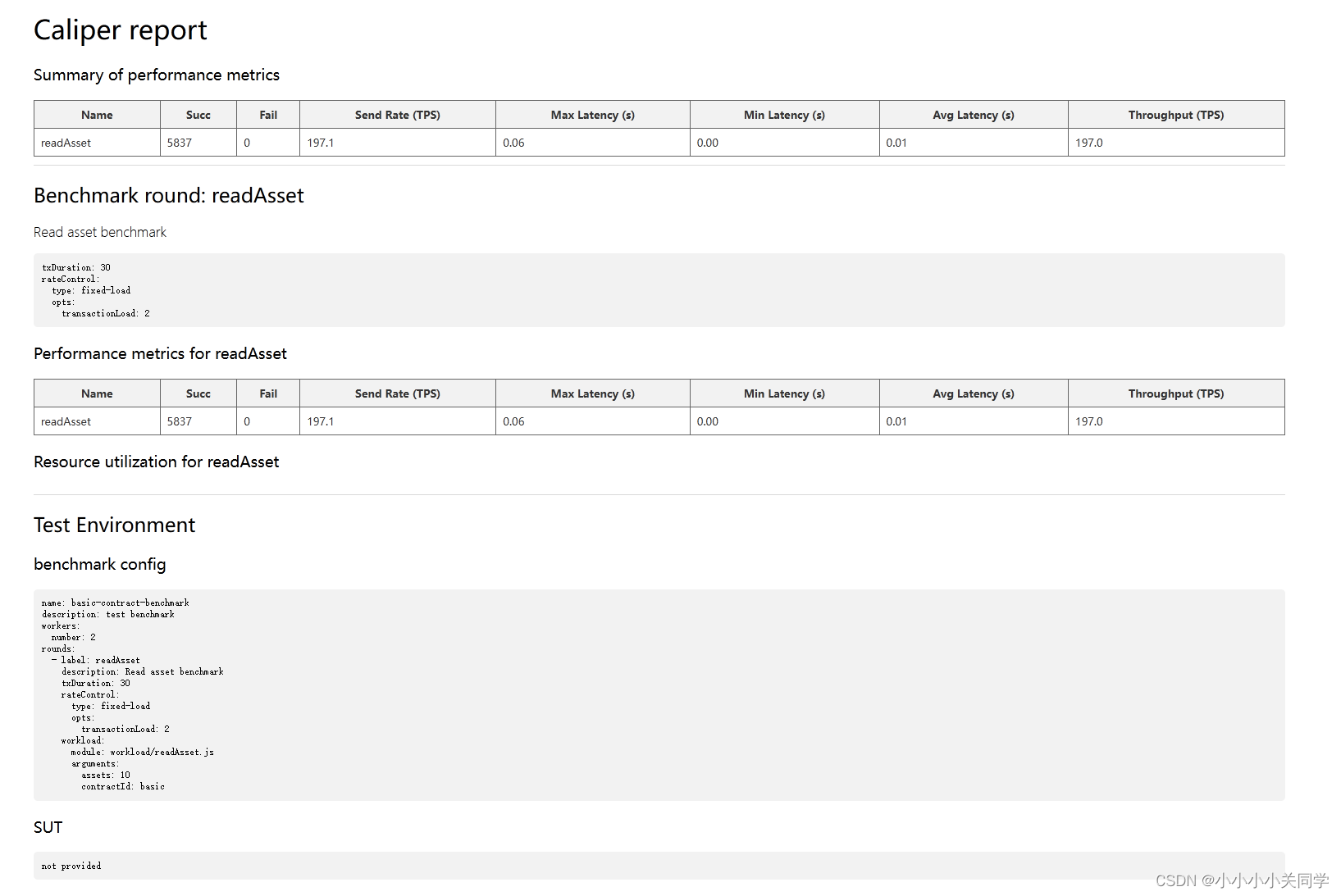
使用Caliper对Fabric地basic链码进行性能测试
如果你需要对fabric网络中地合约进行吞吐量、延迟等性能进行评估,可以使用Caliper来实现,会返回给你一份网页版的直观测试报告。下面是对test-network网络地basic链码地测试过程。 目录 1. 建立caliper-workspace文件夹2. 安装npm等3. calipe安装4. 创建…...

一台是阿里云,一台是腾讯云,一台是华为云,一台是百度云等多种公有云混合安装K8S集群
1. 修改主机名称和添加hosts #永久修改主机名 hostnamectl set-hostname master && bash #在master01上操作,阿里云服务器 hostnamectl set-hostname worker1 && bash #在node01上操作,阿里腾讯云服务器 hostnamectl set-ho…...

期末速成数据库极简版【查询】(3)
目录 多表查询 【8】多表连接——内连接 🙂等值连接 🙂自然连接 🙂非等值连接 【9】多表连接——外连接 【10】交叉连接不考 【11】联合查询 【12】扩展多表连接 【13】嵌套查询 🙂 多表查询 【8】多表连接——内连…...

人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101
然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而, 构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题. 比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值. 可以看到,这个带有一个不等式的条件,…...

有关光伏电站绝缘阻抗异常排查分析-安科瑞 蒋静
近几年,光伏发电技术迅猛发展,光伏扶贫电站及分布式光伏使光伏发电走进千家万户。然而光伏发电设备运行期间仍存在隐患。及时发现并解决*常见异常运行故障,可以很大地提高光伏发电设备可利用率,是保证光伏发电设备正常运行、满足收…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
