【面试常考题目】五种方法解决“如何在n个无序数组中找出它的中位数(java)”问题
1.3 从N个数组中找到中位数,每一个数组可能乱序
在LeetCode上,"寻找多个数组的中位数"这类问题通常是由两个数组合并中位数问题(即LeetCode第4题)的变种或扩展。直接对应于多个数组合并后寻找中位数的题目在LeetCode上并不常见,但是可以通过扩展第4题的解决方案来处理。
处理多个数组合并后寻找中位数的问题,有几种可能的方法:
-
合并后排序:将所有数组合并成一个大数组,然后对这个数组进行排序,最后找到中位数。这种方法简单直接,但如果数组总长度非常大时,可能效率不高。
-
n路归并排序:合并的时候先将各个数组排序,然后采用n路归并的方式不断的将有序值取出(会用到数组指针,每一个元素对应其数组被取出元素的进度),直至取出到总长度的一半,时间复杂度为(n*logx)+O(TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),后者为这n个数组的总长度。
-
(n路归并的优化)优先队列(堆):使用最小堆(或最大堆)逐个合并数组。每次从堆中取出最小(或最大)元素,直到达到总长度的一半,以此找到中位数。这种方法比直接排序更高效一些。
-
基于快速排序的选择方法(效率最快):基于215. 数组中的第K个最大元素想出来的一种方法,首先需要将n个数组合并,然后对其基于215题进行求解
-
分治+二分法:这是参考LeetCode第4题的一种解决方案。LC第四题是从两个有序数组通过二分找到中位数,那么我们可以先将各个子数组排序,通过分治将数组两两合并成两个大数组,然后再调用LC第四题的方法api完成最终的中位数查找。
尽管LeetCode上可能没有直接对应多个数组合并寻找中位数的题目,上述方法提供了一些处理此类问题的思路。在实际编程挑战或面试中,这些方法可能会派上用场。
1.3.1 合并后排序(略)
1.3.2 合并的时候先将各个数组排序,然后采用n路归并的方式不断的将有序值取出(会用到数组指针,每一个元素对应其数组被取出元素的进度),直至取出到总长度的一半,时间复杂度为(nlogx)+O(n*TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),后者TL为这n个数组的总长度。
1 详细步骤
您的方法是一个有效的解决方案,它结合了排序和n路归并排序的思想来找到多个数组中的中位数。以下是对您方法的具体分析:
-
先排序:首先对每个数组进行排序。这确保了每个数组内部是有序的,是归并过程中的关键前提。
-
n路归并:利用归并排序的思路,您维护了一个指针数组来追踪每个数组的当前位置。在每一步中,您会从所有数组的当前位置中选出最小的元素,并将相应数组的指针向前移动一位。
-
取出到总长度的一半:由于中位数是位于排序后数组的中间位置,您只需要进行归并操作直到达到所有数组元素总数的一半。这样就可以找到中位数,无需完全归并所有数组。
这种方法的优点是,它避免了对整个合并后的数组进行完整排序,从而减少了不必要的计算,特别是在数据量很大时更有效率。另外,这种方法适用于数组初始时无序的情况,使其成为解决此类问题的一个实用方案。
2 代码实现
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Random;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(5)+1;for (int i = 0; i < n; i++) {int size= random.nextInt(10)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){list.forEach((o)->{Collections.sort(o);});int n= list.size();if(n==0) return 0.0f;int[]ps=new int[n];int tl=0;for (int i = 0; i < n; i++) {tl+=list.get(i).size();}// corner caseif(tl==1)return list.get(0).get(0);int mid=tl/2;int p=0;int preV=Integer.MAX_VALUE,curV=Integer.MAX_VALUE;while(p<mid+1){int minV=Integer.MAX_VALUE,pos=0;//从n个数组中找到最小那一个及其指针for (int i = 0; i < n; i++) {if(ps[i]<list.get(i).size()&&minV>list.get(i).get(ps[i])){minV=list.get(i).get(ps[i]);pos=i;}}ps[pos]++;//更新当前加入数组的值及其前一个有序值preV=curV;curV=minV;p++;}//总长度为偶数时的返回值if(tl%2==1)return preV;return (float) ((preV+curV)/2.0);}
}1.3.3 优先队列(对1.3.2方法的改进):使用一个能装n个元素最小堆逐个合并数组。每次从堆中pop取出最小元素,同时会从pop出的元素所属的数组中再取出一个元素使其填满n个,直到达到总长度的一半,以此找到中位数。这种方法比直接排序更高效一些。
1 详细步骤
使用优先队列(堆)来找到多个数组的中位数是一种高效的方法,特别是当处理多个大型数组时。这种方法的关键在于逐步合并这些数组,同时保持总体的运行效率。以下是具体的步骤和解释:
-
初始化优先队列:首先,创建一个最小堆(或最大堆,取决于具体实现)。优先队列(堆)将用于存储每个数组中的元素,同时保持它们的排序顺序。
-
填充堆:遍历每个数组,将每个数组的第一个元素(假设数组已排序)加入到优先队列中。为了追踪每个元素属于哪个数组以及在其数组中的位置,你可能需要存储额外的信息,比如数组索引和元素索引。
-
逐步取出元素:从优先队列中逐个取出元素。由于优先队列是一个最小堆(或最大堆),每次都能够取出当前所有数组中的最小(或最大)元素。
-
继续填充堆:每当从优先队列中取出一个元素,就从该元素所属的数组中取出下一个元素(如果存在)并将其加入到优先队列中。这样做可以保持堆中始终有所有数组中当前未处理的最小(或最大)元素。
-
找到中位数:重复上述过程,直到从优先队列中取出了总长度一半的元素。此时,取出的最后一个元素(或者最后两个元素的平均值,取决于总长度是奇数还是偶数)就是中位数。
这种方法的时间复杂度主要由优先队列的操作决定,即O(n log k),其中n是所有数组中总元素的数量,k是数组的数量。这比直接合并所有数组后进行排序的O(n log n)更高效,特别是当k远小于n时。此外,这种方法的空间复杂度为O(k),因为优先队列中最多同时包含k个元素。
2 代码实现
import java.util.*;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(2)+1;for (int i = 0; i < 2; i++) {int size= random.nextInt(2)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){list.forEach((o)->{Collections.sort(o);});int n= list.size();if(n==0) return 0.0f;int tl=0;for (int i = 0; i < n; i++) {tl+=list.get(i).size();}// corner caseif(tl==1)return list.get(0).get(0);// entry<arr_id,pos>PriorityQueue<Map.Entry<Integer,Integer>>pq=new PriorityQueue<>((o1,o2)->(list.get(o1.getKey()).get(o1.getValue())-list.get(o2.getKey()).get(o2.getValue())));for (int i = 0; i < n; i++) {pq.offer(new AbstractMap.SimpleEntry<>(i,0));}int mid=tl/2;int p=0;int preV=Integer.MAX_VALUE,curV=Integer.MAX_VALUE;while(p<mid+1){//从n个数组中找到最小那一个及其指针Map.Entry<Integer,Integer>e=pq.poll();int arrId=e.getKey();//属于哪一个数组int pos=e.getValue();//进度指针if(pos+1<list.get(arrId).size()){Map.Entry<Integer,Integer>ne=new AbstractMap.SimpleEntry<>(arrId,pos+1);pq.offer(ne);}//更新当前加入数组的值及其前一个有序值preV=curV;curV=list.get(arrId).get(pos);p++;}if(tl%2==1)return curV;//总长度为偶数时的返回值return (float) ((preV+curV)/2.0);}
}3 时间复杂度:比1.3.2复杂度更低
时间复杂度为(nlogx)+O(log(n)*TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),TL后者为这n个数组的总长度。
1.3.4 基于快速排序的选择方法
1 思路
参考LC215数组中的第K个最大元素,这个题采用了基于快速排序的选择方法,时间复杂度是O(n),我们知道对于长度为n的数组,n为奇数时,n中位数即是第(n/2+1)小的元素,n为偶数时,n中位数即是第(n/2)小的元素和第(n/2+1)小的元素元素之和的一半。我们知道无论k是多少,最坏的时间复杂度为O(n)
2 代码
假设所有数组的总长度为X,则其时间和空间复杂度均为O(X)
import java.util.*;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(2)+1;for (int i = 0; i < 4; i++) {int size= random.nextInt(2)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){List<Integer>tmp=new ArrayList<>();int n=list.size();//合并所有无序的数组for (int i = 0; i < n; i++) {tmp.addAll(list.get(i));}int mid=tmp.size()/2;if(tmp.size()%2==1){return findK(tmp,mid,0,tmp.size()-1);}else{return (float) ((findK(tmp,mid-1,0,tmp.size()-1)+findK(tmp,mid,0,tmp.size()-1))/2.0);}}// 参考LC215. 数组中的第K个最大元素的解法static int findK(List<Integer>ls, int k, int l, int r){Random random=new Random();int rp= random.nextInt(r-l+1)+l;swap(ls,r,rp);int base=ls.get(r);int low=l,high=r;for (int i = l; i <= high;) {if(ls.get(i)>base){swap(ls,i,high--);}else if(ls.get(i)<base){swap(ls,i++,low++);}else {i++;}}if(k<low){return findK(ls, k,l,low-1);}else if(k>=low&&k<=high){return ls.get(low);}return findK(ls,k,high+1,r);}static void swap(List<Integer>ls, int i, int j){int t=ls.get(i);ls.set(i,ls.get(j));ls.set(j,t);}
}相关文章:
”问题)
【面试常考题目】五种方法解决“如何在n个无序数组中找出它的中位数(java)”问题
1.3 从N个数组中找到中位数,每一个数组可能乱序 在LeetCode上,"寻找多个数组的中位数"这类问题通常是由两个数组合并中位数问题(即LeetCode第4题)的变种或扩展。直接对应于多个数组合并后寻找中位数的题目在LeetCode上…...

打包CSS
接上一个打包HTML继续进行CSS的打包 1.在之前的文件夹里的src文件夹创建一个css文件 2.在浏览器打开webpack——>中文文档——>指南——>管理资源——>加载CSS 3.复制第一句代码到终端 4.复制下图代码到webpack.config.js脚本的plugins:[.....]内容下…...

Java项目开发,业务比较复杂如何减少bug
Java项目开发,业务比较复杂如何减少bug 当Java开发工作涉及复杂业务时,可以采取以下方法来减少bug的数量: 1、深入了解业务需求 充分了解业务需求,与业务人员进行充分的沟通和交流,确保对需求的理解正确。在需求分析…...

[EFI]Atermiter X99 Turbo D4 E5-2630v3电脑 Hackintosh 黑苹果efi引导文件
硬件型号驱动情况主板 Atermiter X99 Turbo D4 处理器 Intel Xeon E5-2630v3 已驱动内存Desktop DDR4 2666 MHz已驱动硬盘Netac NV7000已驱动显卡AMD Radeon RX 5700xt已驱动声卡瑞昱 英特尔 High Definition Audio 控制器ALC897已驱动网卡LucyRTL8125已驱动无线网卡蓝牙Broad…...

map.getOrDefault
map.getOrDefault 是 Java 中的一个方法,用于从 Map 中获取指定键的值,如果键不存在,则返回指定的默认值。 方法签名如下: V getOrDefault(Object key, V defaultValue) 其中,key 是要获取值的键,defaul…...
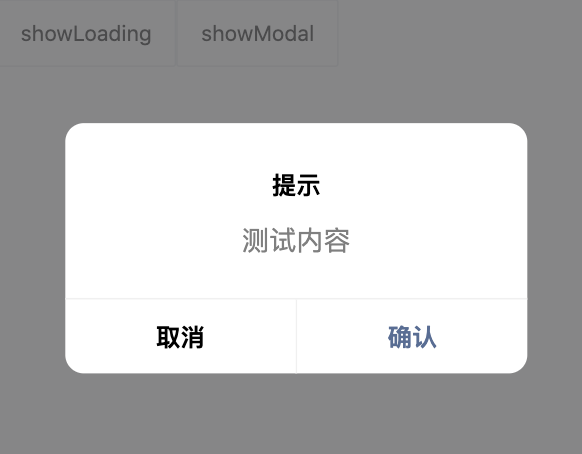
vue3移动端脚手架(纯净,集成丰富)
概述 一个纯净的移动端框架 ,用到了 Vue3 vuex Vite3 Vant3 sass eslint stylelint htmlhint husky commitlint axios axios-adapter VConsole 自定义全局 loading ,自定义函数式 dialog (api模仿微信小程序)&#x…...
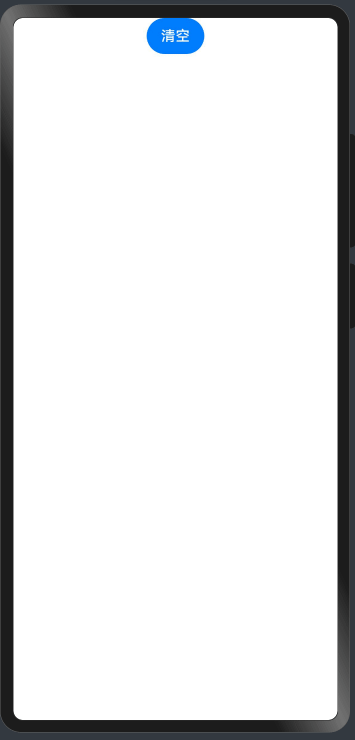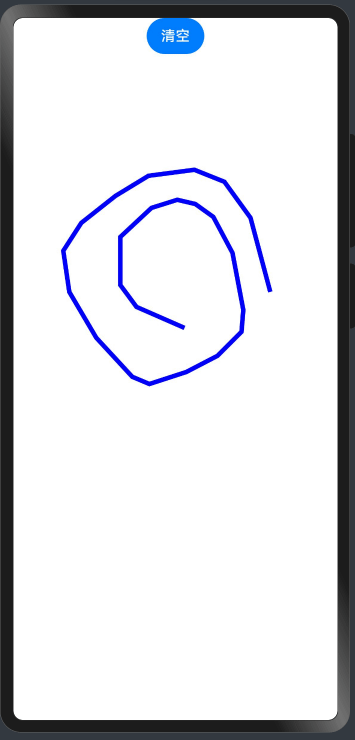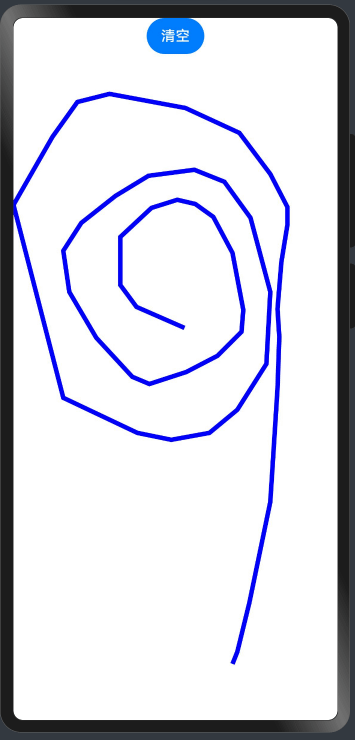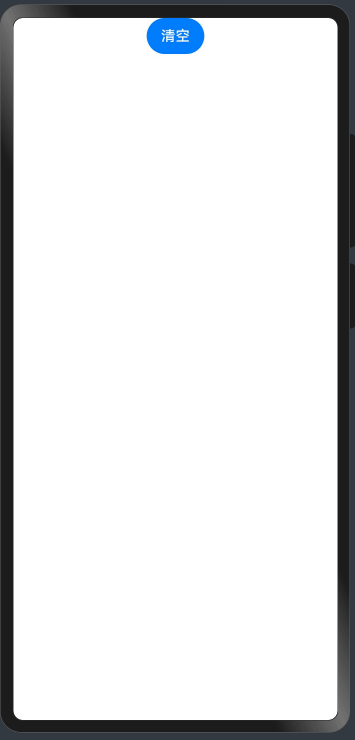
HarmonyOS应用开发-手写板
这是一个基于HarmonyOS做的一个手写板应用,只需要简单的几十行代码,就可以实现如下手写功能以及清空画布功能。 一、先上效果图: 二、上代码 Entry Component struct Index {//手写路径State pathCommands: string ;build() {Column() {//…...

Python中的logging介绍
Python中的logging模块是一个强大的、灵活的、可配置的日志记录系统。它允许你在不修改源代码的情况下记录错误和调试信息,同时也可以对日志信息进行各种处理,例如写入到文件、输出到控制台、记录到数据库等。 logging模块提供了一种用于日志记录的通用接…...
ClickHouse集成JDBC表引擎详细解析)
ClickHouse(17)ClickHouse集成JDBC表引擎详细解析
JDBC 允许CH通过JDBC连接到外部数据库。 要实现JDBC连接,CH需要使用以后台进程运行的程序 clickhouse-jdbc-bridge。 该引擎支持Nullable数据类型。 建表 CREATE TABLE [IF NOT EXISTS] [db.]table_name (columns list... ) ENGINE JDBC(datasource_uri, exte…...
利用CRM系统分析客户行为:精细掌握市场动态
CRM客户关系管理软件在客户行为分析方面发挥着重要作用。通过CRM客户管理系统,企业可以更加便捷地统计客户的行为特征、消费习惯和消费需求,从而洞察市场趋势,帮助企业管理者精准制定营销策略。本文将通过购物篮分析的例子向您介绍CRM客户管理…...
15Linux、GIT及相关相似面试题、PostMan
Linux和git相似是命令相关的层次结构相似 Linux Linux Linux常用操作_linux操作-CSDN博客 程序员常用的10个Linux命令_简介linux系统中的10个常用命令及功能-CSDN博客 help help 命令 :获得 shell 内置命令的帮助信息,常用形式 help cd ls --help …...

游戏中小地图的制作__unity基础开发教程
小地图的制作 Icon标识制作制作摄像机映射创建地图UI效果“不一样的效果” 在游戏中经常可以看到地图视角的存在,那么地图视角是如何让实现的呢? 这一期教大家制作一个简易的小地图。 💖点关注,不迷路。 老样子,我们还…...

sqlite3 --- SQLite 数据库 DB-API 2.0 接口模块
源代码: Lib/sqlite3/ SQLite 是一个C语言库,它可以提供一种轻量级的基于磁盘的数据库,这种数据库不需要独立的服务器进程,也允许需要使用一种非标准的 SQL 查询语言来访问它。一些应用程序可以使用 SQLite 作为内部数据存储。可…...
——如果提高数据样本质量)
做数据分析为何要学统计学(0)——如果提高数据样本质量
样本是数据分析的关键,直接影响研究成果质量。如果样本质量不高,即使使用再好的分析方法,也无法得出理想的结论。所以数据学科圈里有句名言“数据比方法更重要”。所以如何提高数据样本的质量是保证研究成果质量的第一步,虽然这一…...

ubuntu18.04配置cuda+cudnn+tensorrt+anconda+pytorch-gpu+pycharm
一、显卡驱动安装 执行nvidia-smi查看安装情况 二、cuda安装 cuda官网下载cuda_11.6.2_510.47.03_linux.run,安装执行 sudo sh cuda_11.6.2_510.47.03_linux.run提升安装项,驱动不用安装,即第一项(Driver)ÿ…...
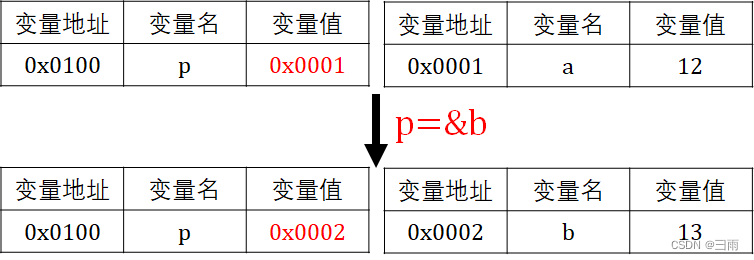
C++ 指针常量和常量指针的区别
指针常量 指针常量:顾名思义它就是一个常量,但是是指针修饰的。 格式为: int * const p //指针常量在这个例子下定义以下代码: int a,b; int * const p&a //指针常量 //那么分为一下两种操作 *p9;//操…...

如何截取Hive数组中的前N个元素?
文章目录 1、需求描述2、使用索引3、使用posexplode()4、转换为字符串操作 1、需求描述 需求:截取任意给定数组中的前N个元素,返回截取后的子数组 假设我们有如下三种类型的Hive数组: select array(1,2,3,4) -- [1,2,3,4] selec…...
iPaaS架构深入探讨
在数字化时代全面来临之际,企业正面临着前所未有的挑战与机遇。技术的迅猛发展与数字化转型正在彻底颠覆各行各业的格局,不断推动着企业迈向新的前程。然而,这一数字化时代亦衍生出一系列复杂而深奥的难题:各异系统之间数据孤岛、…...
UE4/UE5 修改/还原场景所有Actor的材质
使用蓝图方法: 1.修改场景所有Actor 材质: Wirframe:一个材质类 MatList:获取到的所有模型的全部材质 的列表 TempAllClass:场景中所有获取的 Actor 的列表 功能方法如下: 蓝图代码可复制在:…...
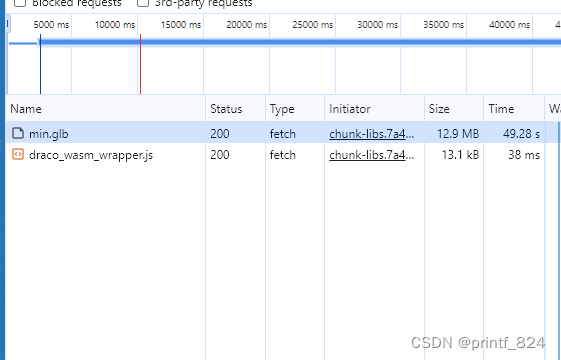
Three.js + Vue 处理glb文件过大问题(DRACOLoader加载压缩glb)
起因,three.js editer导出的glb文件过于庞大,导致部署后文件加载过久 解决方法: 第一步(得有个blender),压缩: 导出时把压缩勾选上 这时候我们会得到一个glb文件,但与three.js edite…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
