c语言青蛙跳台阶

"青蛙跳台阶"问题是一个经典的动态规划问题,经常被用来解释动态规划的基本概念。问题的描述是:假设一只青蛙可以跳上1级或2级台阶,如果有n级台阶,那么青蛙有多少种跳法。
在C语言中,我们可以使用动态规划来解决这个问题。下面是一个示例代码:
- #include <stdio.h>
- long long frogJump(int n) {
- if (n <= 2) {
- return n;
- }
- long long dp[n+1];
- dp[1] = 1;
- dp[2] = 2;
- for (int i = 3; i <= n; i++) {
- dp[i] = dp[i-1] + dp[i-2];
- }
- return dp[n];
- }
- int main() {
- int steps;
- printf("请输入台阶数:");
- scanf("%d", &steps);
- printf("青蛙跳上%d级台阶的方法数为:%lld\n", steps, frogJump(steps));
- return 0;
- }
在这个代码中,我们首先检查台阶数是否小于或等于2。如果是,我们直接返回台阶数,因为青蛙可以直接跳上去。如果不是,我们初始化一个数组dp,其中dp[i]表示跳上i级台阶的方法数。然后我们用一个循环来计算dp数组的值,最后返回dp[n],即跳上n级台阶的方法数。
这个问题的关键在于理解,青蛙跳上n级台阶的方法数等于跳上n-1级台阶和n-2级台阶的方法数的和。这是因为青蛙可以选择跳上一级台阶,或者跳上两级台阶。所以,我们用一个动态规划的思路来解决这个问题,即通过计算并保存每一级台阶的方法数,然后再利用这些保存的方法数来计算更高级台阶的方法数。
上述代码中的主函数首先从用户那里获取台阶数,然后调用frogJump函数来计算青蛙跳上这么多台阶的方法数,并将结果打印出来。
需要注意的是,由于我们使用了一个long long类型的数组来保存方法数,所以这个程序可以计算出相当大的台阶数的结果。然而,由于计算机资源的限制,如果台阶数过大,可能会导致溢出错误。为了避免这种情况,可以使用更复杂的算法来减少内存的使用,或者使用其他编程语言和工具来获取更准确的结果。
另外,如果你想在C语言中实现斐波那契数列,可以直接计算而不需要动态规划。对于n级台阶,就是斐波那契数列的第n项,可以通过递归或迭代的方式直接计算出来。以下是迭代的实现方式:
- #include <stdio.h>
- long long fibonacci(int n) {
- if (n <= 0) {
- return 0;
- } else if (n == 1) {
- return 1;
- } else {
- long long a = 0, b = 1;
- for (int i = 2; i <= n; i++) {
- long long temp = a + b;
- a = b;
- b = temp;
- }
- return b;
- }
- }
- int main() {
- int steps;
- printf("请输入台阶数:");
- scanf("%d", &steps);
- printf("青蛙跳上%d级台阶的方法数为:%lld\n", steps, fibonacci(steps));
- return 0;
- }
在这个代码中,我们用一个循环来计算斐波那契数列的第n项,然后返回结果。这种方法比动态规划的方法更简单,但是它需要更多的计算,特别是当n非常大的时候。
当然,还有更多的优化方式可以提高计算斐波那契数列的效率。例如,可以使用缓存来存储已经计算过的值,以避免重复计算。或者使用更高效的算法,例如快速幂算法。还可以使用更高效的编程语言和工具,例如Python的内置函数或者使用GPU进行并行计算。
另外,这个问题的实际应用不仅仅是计算斐波那契数列。它还可以被用来解决其他的问题,例如计算组合数或者解决旅行者问题。因此,可以根据具体的问题场景选择最合适的解决方法。
最后,需要注意的是,虽然计算机科学在很大程度上已经解决了大规模计算的问题,但是仍然存在一些问题需要更复杂的算法或者更多的资源来解决。因此,即使是最先进的计算机科学技术,也有可能需要不断的改进和发展才能满足不断增长的计算需求。
相关文章:

c语言青蛙跳台阶
"青蛙跳台阶"问题是一个经典的动态规划问题,经常被用来解释动态规划的基本概念。问题的描述是:假设一只青蛙可以跳上1级或2级台阶,如果有n级台阶,那么青蛙有多少种跳法。 在C语言中,我们可以使用动态规划来…...

IntelliJ IDEA 2023.3 最新版如何试用?IntelliJ IDEA 2023.3 最新版试用方法
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Java参数校验详解:使用@Valid注解和自定义注解进行参数验证
很多时候我们需要使用不少if、else等等逻辑判断及验证,这样在进行一些重复的参数校验会很麻烦,且以后要维护也会吃力。 而这样就可以使用javax.validation。验证(Validation)常见的验证操作包括验证数据的类型、格式、长度、范围、…...

多维时序 | MATLAB实现BWO-CNN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测
多维时序 | MATLAB实现BWO-CNN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现BWO-CNN-BiGRU-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLAB实现BWO-CNN-B…...

C++ 中的引用
文章目录 C 引用的应用1. 修改函数中传递的参数2. 避免复制大型结构3. for 循环中修改所有对象4. for 循环中避免复制对象 References vs Pointers引用的限制使用引用的优点练习Quesition 1Question 2Question 3Question 4Question 5Question 6 如果一个变量被声明为引用&#…...

MQ-Det: Multi-modal Queried Object Detection in the Wild
首个支持视觉和文本查询的开放集目标检测方法 NeurIPS2023 文章:https://arxiv.org/abs/2305.18980 代码:https://github.com/YifanXu74/MQ-Det 主框图 摘要 这篇文章提出了MQ-Det,一种高效的架构和预训练策略,它利用文本描述的…...

HarmonyOS应用开发初体验
9月25日华为秋季全场景新品发布会上,余承东宣布,全面启动鸿蒙原生应用,HarmonyOS NEXT开发者预览版将在2024年第一季度面向开发者开放。 最近鸿蒙开发可谓是火得一塌糊涂,各大培训平台都开设了鸿蒙开发课程。美团发布了鸿蒙高级工…...

《C++新经典设计模式》之第4章 策略模式
《C新经典设计模式》之第4章 策略模式 策略模式.cpp 策略模式.cpp #include <iostream> #include <memory> using namespace std;// if或switch分支不稳定,经常改动时,考虑引入算法独立到策略类中去实现// 依赖倒置原则 // 高层组件不应该依…...

【方法】PowerPoint“只读方式”如何取消?
PPT设置了以“只读方式”打开,可以保护文件无法编辑更改,那后续不需要保护了,或者想要编辑文件,要如何取消“只读方式”呢? 首先,我们要看看PPT设置的是哪种“只读方式”。 如果PPT设置的是无密码“只读方…...

MySQL数据库概念与实践
MySQL数据库概念与实践 1. 概念 MySQL是一种常用的关系型数据库管理系统,具有丰富的功能和广泛的应用。在本篇博客中,我们将介绍MySQL数据库的一些重要概念和相关知识。 存储引擎 存储引擎是MySQL数据库用于存储、更新和查询数据的技术实现方法。MyS…...
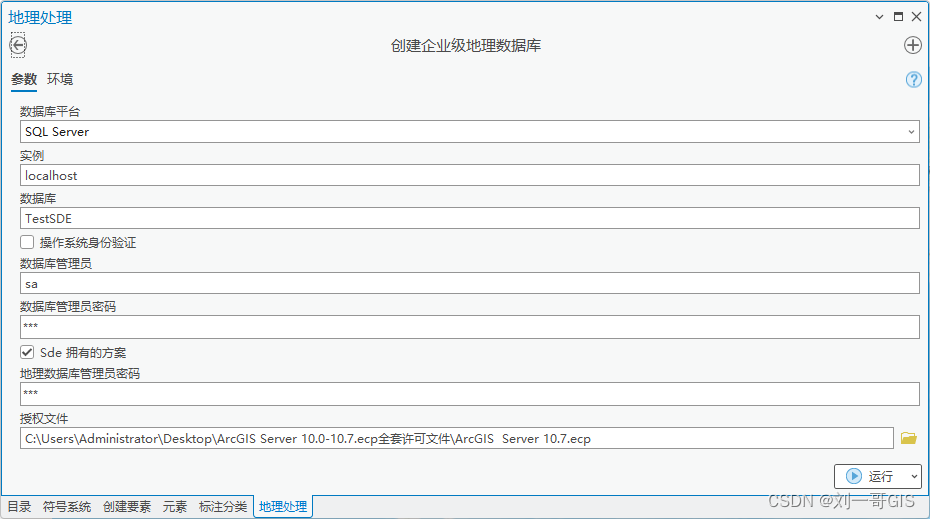
【ArcGIS Pro微课1000例】0052:基于SQL Server创建企业级地理数据库案例
文章目录 环境搭建创建企业级数据库连接企业级数据库环境搭建 ArcGIS:ArcGIS Pro 3.0.1Server.ecp:版本为10.7SQL Server:版本为SQL Server Developer 2019创建企业级数据库 企业级地理数据库的创建需要通过工具箱来实现。工具位于:数据管理工具→地理数据库管理→创建企业…...
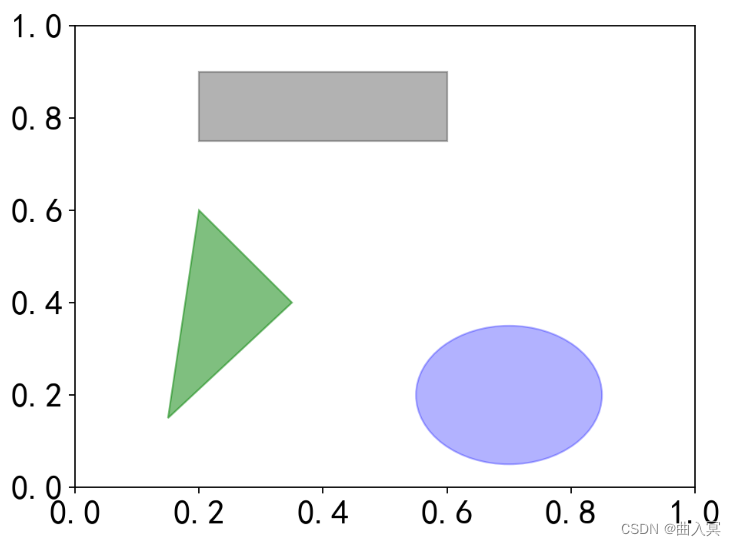
深度学习——第3章 Python程序设计语言(3.7 matplotlib库)
3.7 matplotlib库 目录 1 matplotlib库简介 2 pyplot的plot函数 3 matplotlib基础绘图函数示例 数据可视化有助于深度理解数据。 本节介绍绘制图形的基本方法。 1. matplotlib库简介 matplotlib官网 1.1 matplotlib库概述 matplotlib是Python优秀的数据可视化第三方库&a…...
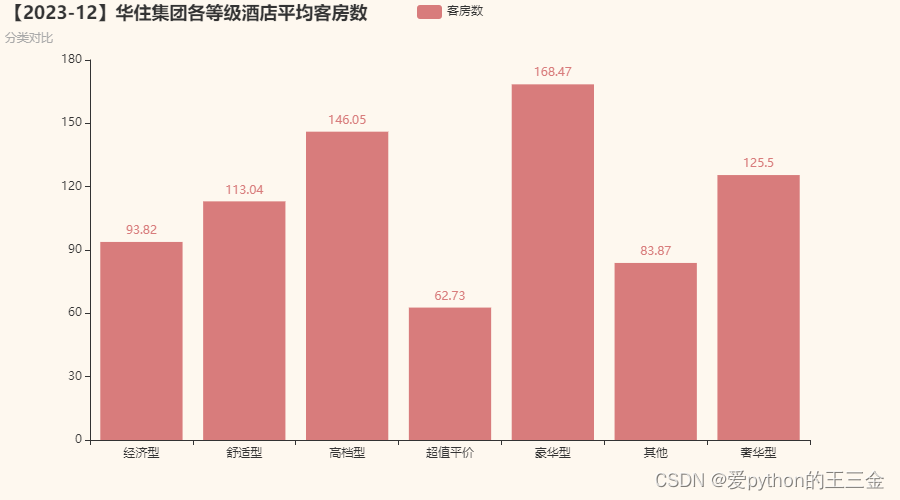
【数据分析实战】酒店行业华住集团门店分布与评分多维度分析
文章目录 1. 写在前面2. 数据集展示3. 多维度分析3.1 门店档次多元化:集团投资战略观察3.1.1 代码实现3.1.2 本人浅薄理解 3.2 门店分布:各省市分布概览3.2.1 代码实现3.2.2 本人浅薄理解 3.3 门店分级评分:服务水平的多维度观察3.3.1 代码实…...
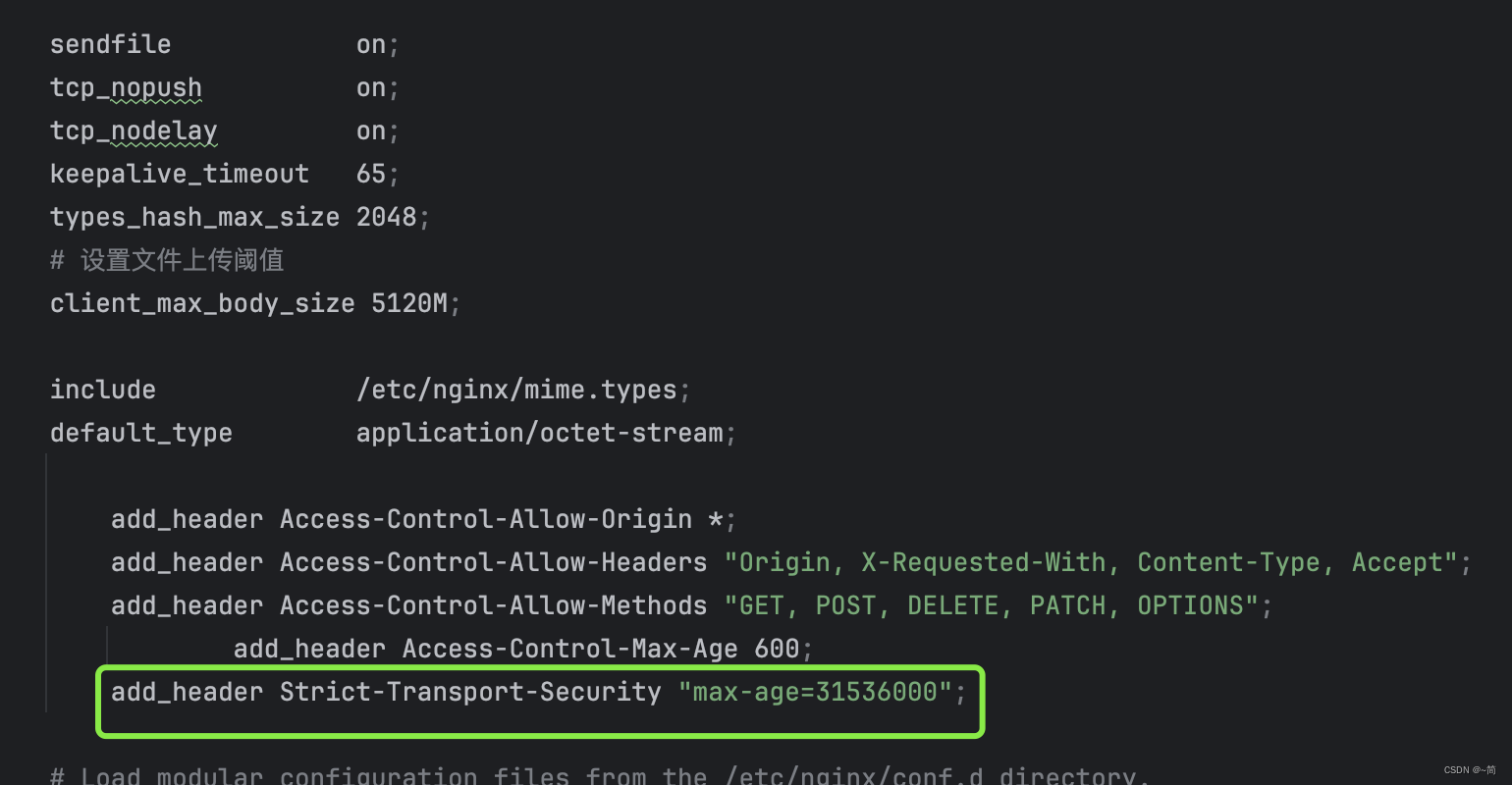
近期Chrome浏览器 不知哪个版本升级后原先http强制跳转到https,导致服务端302强制跳转到http也没反应
关于Chrome更新http强制跳转到https解决方法 近期Chrome浏览器 不知哪个版本升级后原先http强制跳转到https,导致服务端302强制跳转到http也没反应一、F12检查加载的Response Headers中有没有Non-Authoritative-Reason二、找了资料后得到解决方案:三、找…...
【scikit-learn基础】--『数据加载』之样本生成器
除了内置的数据集,scikit-learn还提供了随机样本的生成器。通过这些生成器函数,可以生成具有特定特性和分布的随机数据集,以帮助进行机器学习算法的研究、测试和比较。 目前,scikit-learn库(v1.3.0版)中有2…...

基于 ESP32-S3 的 Walter 开发板
Walter 是一款基于 ESP32-S3 且拥有 5G LTE 连接功能的新型开源开发套件。 近日,比利时公司 DPTechnics BV 推出了一款基于乐鑫 ESP32-S3 且拥有 5G LTE 连接功能的新型开源开发套件。该套件即将在 Crowd Supply 平台上发布,您可以点击此处了解详情。 无…...
Gitlab+GitlabRunner搭建CICD自动化流水线将应用部署上Kubernetes
文章目录 安装Gitlab服务器准备安装版本安装依赖和暴露端口安装Gitlab修改Gitlab配置文件访问Gitlab 安装Gitlab Runner服务器准备安装版本安装依赖安装Gitlab Runner安装打包工具安装docker安装java17安装maven 注册Gitlab Runner 搭建自动化部署准备SpringBoot项目添加一个Co…...

待做-待补充-每个节点做事,时间,以及与角度的关系
文章目录 纲领1.是否可以通过遍历一遍二叉树得到答案2.是否可以通过两颗子树相同问题的答案推导出树的答案(形式为递归)无论哪种思维模式,都需要思考:单独一个二叉树节点,它需要做什么事情?需要在什么时候做 后序判断问题是否和子树相关&…...
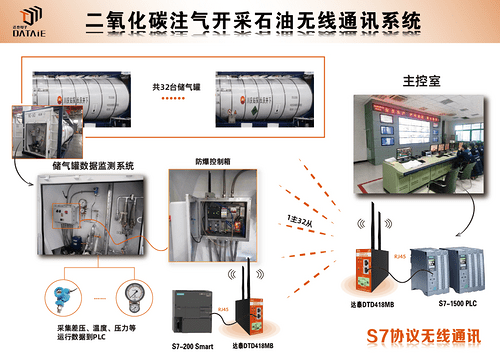
液态二氧化碳储存罐远程无线监测系统
二氧化碳强化石油开采技术,须先深入了解石油储层的地质特征和二氧化碳的作用机制。现场有8辆二氧化碳罐装车,每辆罐车上有4台液态二氧化碳储罐,每台罐的尾部都装有一台西门子S7-200 smart PLC。在注入二氧化碳的过程中,中控室S7-1…...

kafka学习笔记--安装部署、简单操作
本文内容来自尚硅谷B站公开教学视频,仅做个人总结、学习、复习使用,任何对此文章的引用,应当说明源出处为尚硅谷,不得用于商业用途。 如有侵权、联系速删 视频教程链接:【尚硅谷】Kafka3.x教程(从入门到调优…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...
