Lcss算法介绍与应用演示
Lcss算法介绍
LCSS(最长公共子序列,Longest Common Subsequence)算法是一种用于比较两个序列相似度的方法。它寻找两个序列中的最长子序列,这个子序列不需要在原始序列中连续,但必须保持原有序列中元素的相对顺序。LCSS算法在多种领域有着广泛的应用,比如文本比较、生物信息学和轨迹分析。
### LCSS算法的基本概念
1. **子序列**:如果序列Z中的所有元素都按其在序列X中出现的顺序出现在X中,那么Z是X的子序列。例如,Z = [a, b, c] 是 X = [a, d, b, c, e] 的子序列。
2. **最长公共子序列**:对于两个序列X和Y,它们的最长公共子序列是X和Y所有可能的公共子序列中最长的那一个。
### 算法特点
- **非连续性**:LCSS不要求子序列在原始序列中是连续的。
- **保持顺序**:子序列必须保持原序列中元素的相对顺序。
- **长度灵活**:LCSS的长度可以随序列中元素的增加而增加。
### 算法应用
- **文本相似度**:比较两段文本,找出它们的共同元素。
- **生物序列分析**:在DNA序列分析中,寻找共同的基因片段。
- **轨迹分析**:在地理信息系统(GIS)中,比较两个或多个轨迹的相似度。
### 算法实现
LCSS算法通常使用动态规划来实现。动态规划的方法是填充一个矩阵,其中每个元素代表考虑到目前为止的序列X和Y的最长公共子序列的长度。通过比较序列的每个元素,并考虑之前计算的结果,我们可以构建出整个矩阵。最后,矩阵的右下角元素就代表了两个序列的最长公共子序列的长度。
总之,LCSS算法是一种有效的比较两个序列相似度的方法,特别适用于元素顺序重要但不要求连续匹配的情况。
算法应用演示
public class TrajectoryComparison {
/**
* 根据LCSS算法比较两个轨迹。
*
* @param points1 第一个轨迹,表示为[x,y]坐标的数组。
* @param points2 第二个轨迹,与第一个类似。
* @param eps 考虑两点接近的阈值距离。
* @param similarRadiusFactor 用于确定相似点索引范围的因子。
* @return 表示两个轨迹相似度的双精度分数。
*/
public static double compare(double[][] points1, double[][] points2, double eps, double similarRadiusFactor) {
int rows = points1.length + 1;
int columns = points2.length + 1;
double[][] matrix = new double[rows][columns];
// 构建LCSS矩阵
for (int i = 1; i < rows; i++) {
for (int j = 1; j < columns; j++) {
double point1x = points1[i - 1][0];
double point1y = points1[i - 1][1];
double point2x = points2[j - 1][0];
double point2y = points2[j - 1][1];
// 检查点是否足够接近且在相似半径因子范围内
if (distanceBetween(point1x, point1y, point2x, point2y) < eps && Math.abs(i - j) < (Math.min(rows, columns) * similarRadiusFactor)) {
matrix[i][j] = matrix[i - 1][j - 1] + 1;
} else {
matrix[i][j] = Math.max(matrix[i][j - 1], matrix[i - 1][j]);
}
}
}
// 计算相似度分数
return 1 - matrix[rows - 1][columns - 1] / Math.min(rows - 1, columns - 1);
}
/**
* 计算两点之间的欧几里得距离。
*
* @param x1 第一个点的x坐标。
* @param y1 第一个点的y坐标。
* @param x2 第二个点的x坐标。
* @param y2 第二个点的y坐标。
* @return 两点之间的欧几里得距离。
*/
private static double distanceBetween(double x1, double y1, double x2, double y2) {
return Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
}
public static void main(String[] args) {
// 示例测试用例
double[][] trajectory1 = {{0, 0}, {1, 1}, {2, 2}, {3, 3}};
double[][] trajectory2 = {{0, 0}, {1, 1}, {2, 2}, {4, 4}};
double eps = 1.0;
double similarRadiusFactor = 0.5;
double similarityScore = compare(trajectory1, trajectory2, eps, similarRadiusFactor);
System.out.println("相似度分数: " + similarityScore);
}
}
compare函数接受两个轨迹作为输入,并计算它们之间的相似度。distanceBetween`函数计算两点之间的欧几里得距离。最后,`main` 方法提供了一个示例测试用例,用于演示如何使用这个函数计算两个简单轨迹的相似度分数。可以根据实际需求调整 `eps` 和 `similarRadiusFactor` 参数的值。
相关文章:

Lcss算法介绍与应用演示
Lcss算法介绍 LCSS(最长公共子序列,Longest Common Subsequence)算法是一种用于比较两个序列相似度的方法。它寻找两个序列中的最长子序列,这个子序列不需要在原始序列中连续,但必须保持原有序列中元素的相对顺序。LC…...

【SpringBoot】从入门到精通的快速开发指南
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《SpringBoot》。🎯🎯 &…...

每日一练【长度最小的子数组】
一、题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 二、题目解析 经…...

HTML 块级元素与行内元素有哪些以及注意、总结
行内元素和块级元素是HTML中的两种元素类型,它们在页面中的显示方式和行为有所不同。 块级元素(Block-level Elements): 常见的块级元素有div、p、h1-h6、ul、ol、li、table、form等。 块级元素会独占一行,即使没有…...
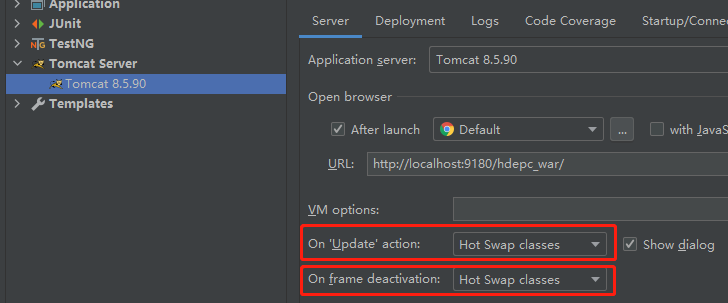
SpringBoot热部署
SpringBoot热部署 借鉴链接🔗:SpringBoot中的热部署 添加devtools依赖和pom插件 <!-- devtools 依赖 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId&…...
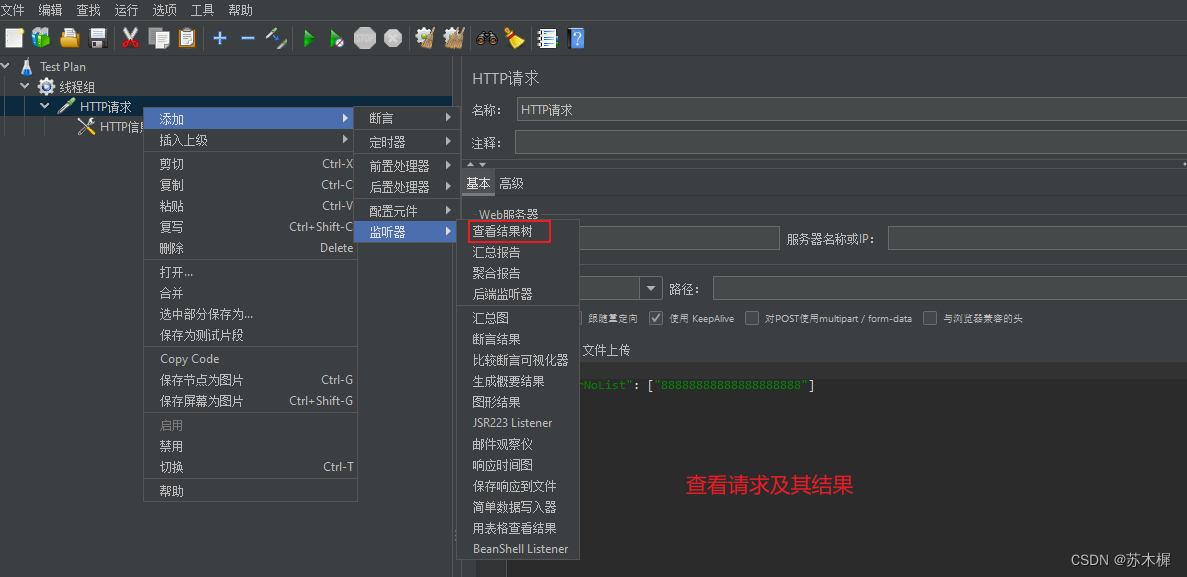
Jmeter入门
一、下载jmeter 官网下载 下载之后解压,在目录/bin下面找到jmeter.bat双击之后即可启动Jmeter。 二、使用 如下左图,选择语言为中文,可以修改测试计划的名称。如下右图,添加线程组 添加线程组 添加http请求 路径传参方式 …...

go集成nacos
1,go集成nacos 注册实例与注销实例 package mainimport ("fmt""github.com/nacos-group/nacos-sdk-go/clients""github.com/nacos-group/nacos-sdk-go/clients/naming_client""github.com/nacos-group/nacos-sdk-go/common/constant"…...

NLP项目实战01--电影评论分类
介绍: 欢迎来到本篇文章!在这里,我们将探讨一个常见而重要的自然语言处理任务——文本分类。具体而言,我们将关注情感分析任务,即通过分析电影评论的情感来判断评论是正面的、负面的。 展示: 训练展示如下…...

Linux vmstat命令:监控系统资源
vmstat命令,是 Virtual Meomory Statistics(虚拟内存统计)的缩写,可用来监控 CPU 使用、进程状态、内存使用、虚拟内存使用、硬盘输入/输出状态等信息。此命令的基本格式有如下 2 种: [rootlocalhost ~]# vmstat [-a…...

php爬虫规则与robots.txt讲解
在进行网页爬虫时,有一些规则需要遵守,以避免违反法律,侵犯网站隐私和版权,以及造成不必要的麻烦。以下是一些常见的PHP爬虫规则: 1. 尊重网站的使用条款:在开始爬取之前,请确保你阅读并理解了…...

Ray使用备注
Ray使用备注 框架介绍 Ray是一种python分布式任务调度框架其支持 无状态的任务并发执行,也支持 有状态的任务按照一定顺序执行其支持 分布式调度器,在一个节点上创建的任务先给本节点的局部调度器,并让本节点自己处理,当资源不够时,再将任务发给全局调度器供其他节点处理其支…...

个人介绍以及毕业去向
CSDN陪伴我从大一到大四,后面也会接着用 写一点大学四年的总结 #总结#理工科#留学 211大学 弃保出国 智能科学与技术 均分88.9 EI论文一篇 数学竞赛和数学建模均为省二 大创评为国家级 全国大学生计算机设计大赛国家三等奖 百度Paddle、大疆RoboMaster、Phytium Te…...
原创度检测,在线文章原创度检测
原创度检测,作为数字时代中内容创作者和学术界广泛关注的话题,正逐渐成为保障知识产权、促进创新发展的不可或缺的工具。今天,我们将深入介绍原创度检测的定义、意义、技术原理、应用领域以及未来趋势。 一、什么是原创度检测? 原…...
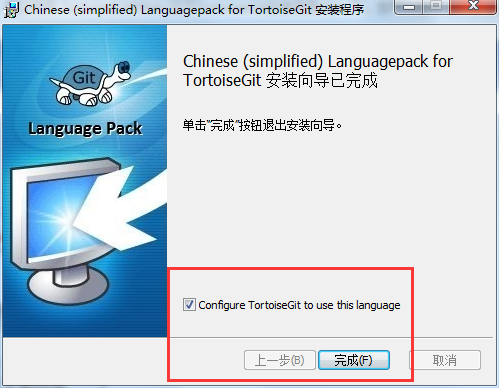
windows下安装git中文版客户端
下载git Windows客户端 git客户端下载地址:Git - Downloads 我这里下载的是Git-2.14.0-64-bit.exe版本 下载TortoiseGit TortoiseGit客户端下载地址:Download – TortoiseGit – Windows Shell Interface to Git TortoiseGit客户端要下载两个&#…...

短视频怎么批量添加水印logo
在现代数字化时代,视频内容已经成为我们日常生活中不可或缺的一部分。然而,当我们辛辛苦苦制作的视频在网络上分享时,常常会遇到被他人盗用或未经授权使用的情况。为了保护我们的创作成果,给视频添加水印logo成为了一种常见的手段…...

一文入门 UUID
UUID简介 UUID代表Universally Unique Identifier,译为全局一标识符。它是一种由软件构建的标准化身份验证方案,用于确保跨多个上下文中的对象都具有唯一性。UUID在各种系统之间确保了严格的唯一性,因此即使在大型分布式环境中,也…...
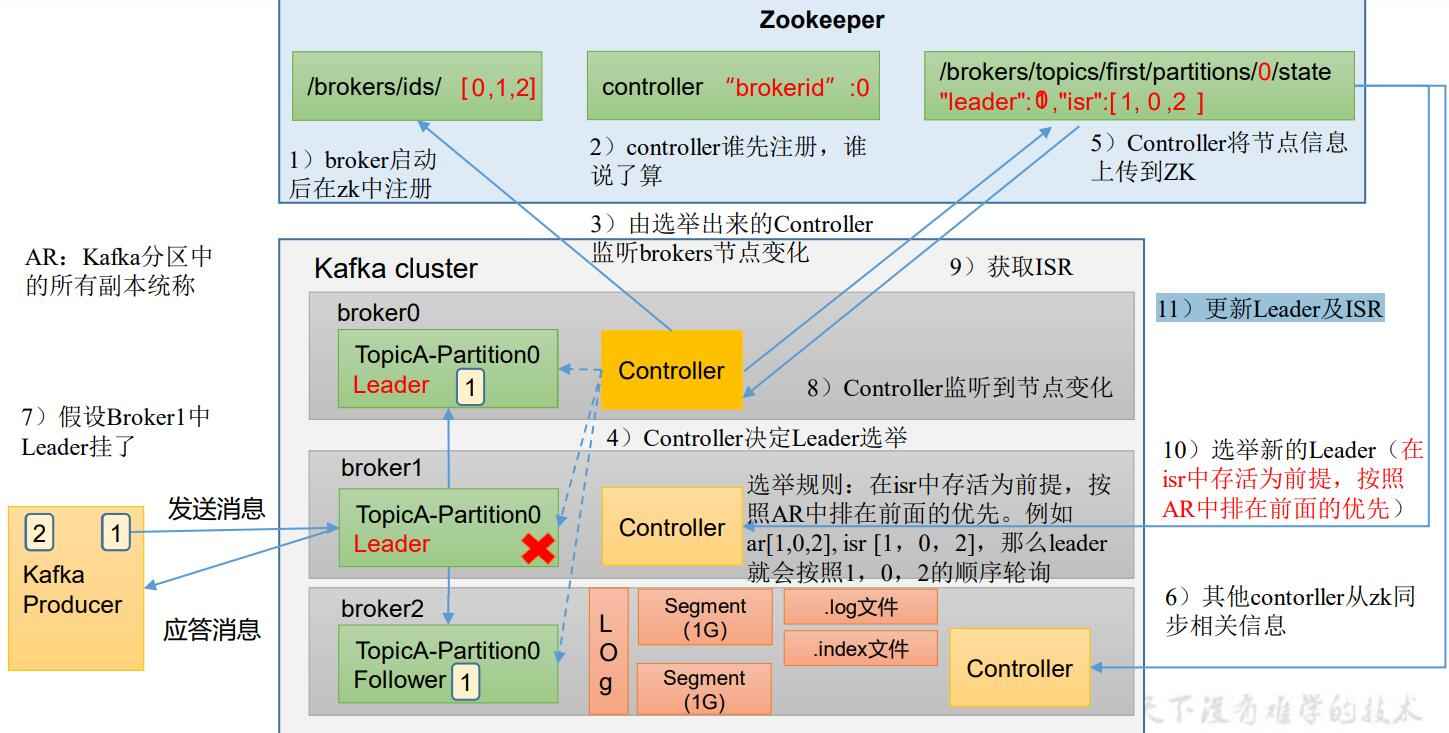
kafka学习笔记--broker工作流程、重要参数
本文内容来自尚硅谷B站公开教学视频,仅做个人总结、学习、复习使用,任何对此文章的引用,应当说明源出处为尚硅谷,不得用于商业用途。 如有侵权、联系速删 视频教程链接:【尚硅谷】Kafka3.x教程(从入门到调优…...
多合一iPhone 解锁工具:iMyFone LockWiper iOS
多合一iPhone 解锁工具 无需密码解锁 iPhone/iPad/iPod touch 上所有类型的屏幕锁定 在几分钟内解锁 iPhone Apple ID、Touch ID 和 Face ID 立即绕过 MDM 并删除 iPhone/iPad/iPod touch 上的 MDM 配置文件 支持所有 iOS 版本和设备,包括最新的 iOS 17 和 iPhone 1…...

在设计和考虑建造室外雨水收集池时需要注意的因素
在设计和建造室外雨水收集池时,需要考虑以下因素: 地质条件:建造雨水收集池需要考虑到地质条件,例如土壤类型、地基承载能力等。这些因素可能对水池的建造和结构产生影响。 气候条件:不同地区的降雨量、湿度、气温等…...

C_5练习题答案
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 下列叙述中错误的是(D)。A.计算机不能直接执行用C语言编写的源程序 B.C程序经C编译程序编译后,生成扩展名为obj的文件是一个二…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
