理解排序算法:冒泡排序、选择排序与归并排序
简介: 在计算机科学中,排序算法是基础且重要的概念。本文将介绍三种常见的排序方法:冒泡排序、选择排序和归并排序。我们将探讨它们的工作原理、特点和适用场景,以帮助读者更好地理解和选择合适的排序方法。
冒泡排序
冒泡排序是一种简单的排序算法。它通过重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。这个过程重复进行,直到没有再需要交换的元素,此时数列已经排序完成。冒泡排序的特点是实现简单,但效率较低,特别是在处理大数据集时。

void BubbleSort(int* a, int n)//使用bool来进阶冒泡 ,当有一层不交换,就代表已经排完序,防止永久时间复杂度都是O(n^2)
{for (int j = 0; j < n; j++){bool exange = false;for (int i = 1; i < n - j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exange = true;}}if (exange == false)break;}}冒泡排序的特性总结:
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
选择排序

选择排序是一种简单直观的排序算法,广泛应用于计算机科学教学和一些基础编程任务中。本文将详细介绍选择排序的工作原理、具体实现步骤、算法特点以及适用场景,帮助读者更好地理解和使用这种排序方法。
一、选择排序的工作原理
选择排序算法的基本思想是:
首先在未排序的序列中找到最小(或最大)的元素,然后将其放置在序列的起始位置,接着再从剩余未排序的元素中继续寻找最小(或最大)的元素,然后放到已排序序列的末尾。这个过程一直重复,直到所有元素都被排序。
二、选择排序的步骤
- 从未排序的序列中找到最小(或最大)的元素。
- 将找到的最小(或最大)元素与序列的第一个元素交换位置(如果最小元素就是第一个元素,则自身和自身交换)。
- 重复上述过程,每次交换后,排序序列的长度就增加一个元素,而未排序序列的长度减少一个元素。
- 当未排序序列的长度减少到0时,排序就完成了。
三、选择排序的特点
- 简单直观:选择排序的算法逻辑简单,易于理解和实现。
- 时间复杂度:在最好、最坏和平均情况下,时间复杂度都是O(n²)。
- 不稳定排序:选择排序不是稳定的排序算法,相等的元素可能在排序过程中改变其原有的顺序。
- 原地排序:选择排序不需要额外的存储空间,它是一种原地排序算法。
四、选择排序的适用场景
由于选择排序的效率较低,它通常不适用于数据量较大的排序任务。然而,在数据量较小或者对算法的时间复杂度要求不高的场景中,选择排序由于其实现的简单性,仍然是一个不错的选择。特别是在教学和学习算法的过程中,选择排序是理解基本排序概念的良好起点。
总结: 选择排序以其简单直观的特点,在编程教学和小规模数据处理中有着一席之地。虽然在处理大量数据时效率不高,但它作为基础排序算法,对于理解更复杂的排序技术提供了重要的基础。
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin; int max = begin;for (int i = begin+1; i <= end; ++i){if (a[i] < a[mini]){mini = i;}if (a[i] > a[max]){max = i;}}Swap(&a[begin], &a[mini]);if (max == begin){max = mini;}Swap(&a[end], &a[max]);begin++;end--;}}归并排序
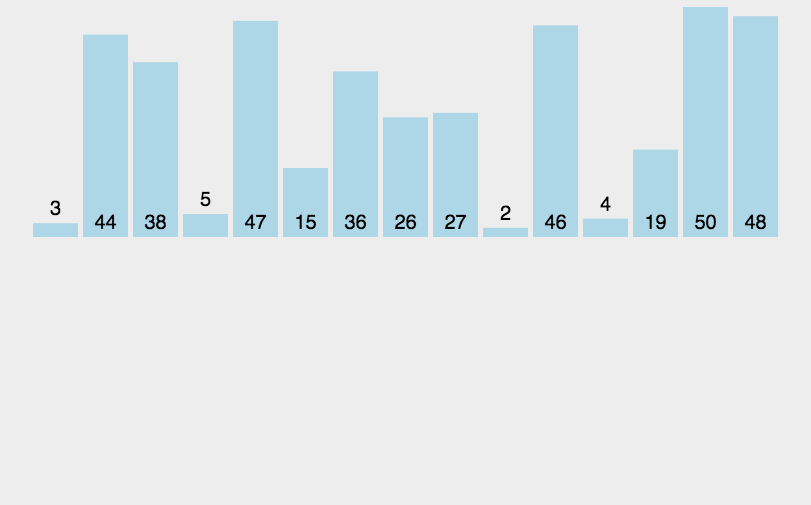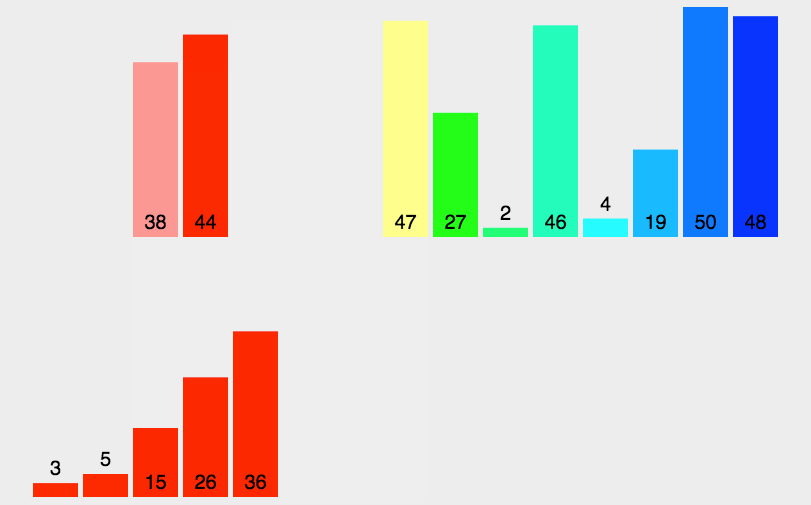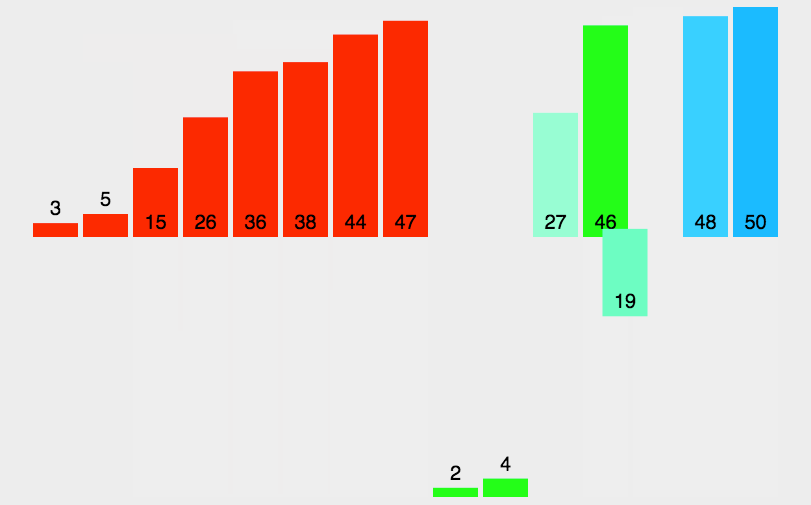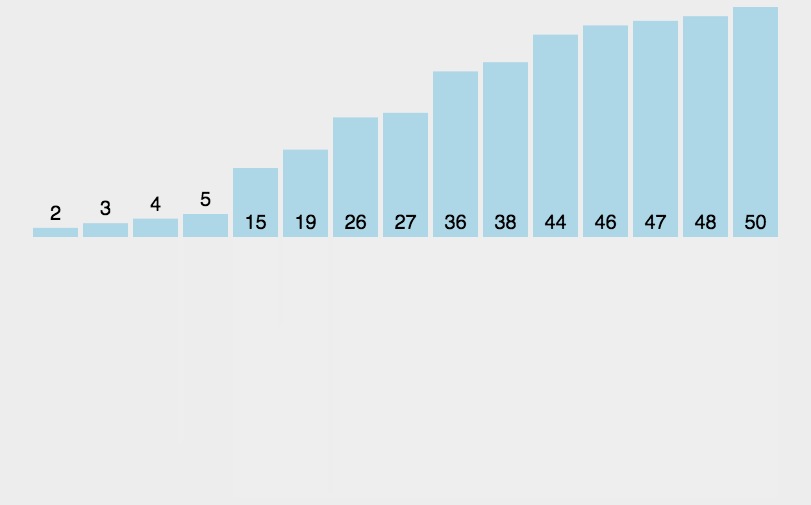
简介: 归并排序是一种高效且稳定的排序算法,通过分治法实现对数据的高效排序。本文旨在详细介绍归并排序的工作原理、具体实现步骤、算法的特点以及适用场景,帮助读者深入理解并有效地应用这种排序方法。
一、归并排序的工作原理
归并排序的核心思想是将两个有序的数组合并成一个更大的有序数组。具体来说,它将原始数组分成两半,分别对这两半进行排序,然后将排序好的两个半部分合并在一起。这个过程是递归进行的,最终达到完全排序的目的。
二、归并排序的步骤
- 分解:将原始数组分解成两个大小大致相等的子数组。
- 解决:递归地对这两个子数组进行归并排序。
- 合并:将两个已排序的子数组合并成一个单一的已排序数组。
三、归并排序的特点
- 高效稳定:归并排序在最坏、最好和平均情况下的时间复杂度均为O(n log n),是一种非常高效的排序算法。同时,它也是一种稳定的排序,即相等的元素在排序后会保持其原有顺序。
- 分治策略:归并排序是分治法思想的典型应用,通过将问题分解为可管理的子问题来简化复杂性。
- 额外空间需求:归并排序需要额外的空间来存储临时数组,这是它的一个缺点。
四、归并排序的适用场景
归并排序非常适合处理大数据集,特别是在数据无法一次性装入内存时。由于其稳定性和高效性,它广泛应用于数据库和文件系统等领域,是处理大规模数据排序的理想选择。
总结: 归并排序以其高效、稳定的特性,在大数据处理和复杂系统中占有重要位置。尽管需要额外的存储空间,但其优越的性能使其成为解决复杂排序问题的强大工具。
void _MergeSort(int* a, int begin, int end, int* tmp)//每次需要开辟数组且要对数组进行分区,所以调用子函数
{int mid = (begin + end) / 2;//[begin , mid] [mid +1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//后序逻辑 归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));}
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
总结: 在本系列博客文章中,我们深入探讨了三种经典的排序算法:冒泡排序、选择排序和归并排序。每种排序方法都有其独特的工作原理和应用场景,从简单直观的冒泡排序和选择排序到高效稳定的归并排序,这些算法为我们提供了不同的数据组织和处理方式。
冒泡排序以其实现的简单性和直观性而闻名,适合用于小数据集和教学目的。选择排序,尽管时间复杂度较高,但在需要减少交换次数的情况下仍是一个不错的选择。归并排序则以其高效率和稳定性在大数据处理中发挥重要作用,尤其适用于无法一次性装入内存的大规模数据集。
理解这些排序算法的原理和特点对于任何涉及数据处理的程序员来说都是至关重要的。它们不仅是计算机科学的基础,也是解决实际问题的强大工具。我们希望这些文章能够帮助读者更好地理解这些基本算法,并在适当的场合中作出恰当的选择。
感谢您阅读本系列关于排序算法的探索。我们期待在未来的文章中继续为您提供更多有价值的技术洞见和实用建议。
相关文章:

理解排序算法:冒泡排序、选择排序与归并排序
简介: 在计算机科学中,排序算法是基础且重要的概念。本文将介绍三种常见的排序方法:冒泡排序、选择排序和归并排序。我们将探讨它们的工作原理、特点和适用场景,以帮助读者更好地理解和选择合适的排序方法。 冒泡排序 冒泡排序是…...
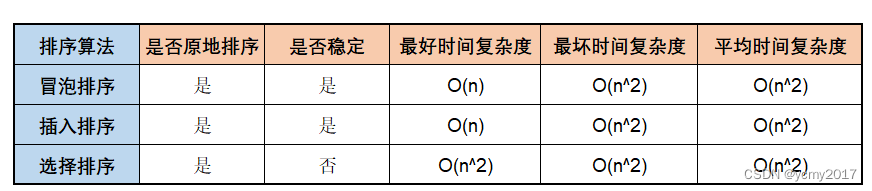
算法-02-排序-冒泡插入选择排序
一般最经典的、最常用的:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。那么我们如何分析一个"排序算法"呢? 1-分析排序算法要点 时间复杂度:具体是指最好情况、最坏情况、平均情况下的时间复杂…...
流量异常-挂马造成百度收录异常关键词之解决方案(虚拟主机)
一.异常现象:流量突然暴涨,达到平时流量几倍乃至几十倍,大多数情况下因流量超标网站被停止。 二.排查原因: 1.首先分析web日志:访问量明显的成倍、几十倍的增加;访问页面不同;访问IP分散并不固…...

磁力计LIS2MDL开发(1)----轮询获取磁力计数据
磁力计LIS2MDL开发.1--轮询获取磁力计数据 概述视频教学样品申请源码下载通信模式速率生成STM32CUBEMX串口配置IIC配置CS设置串口重定向参考程序初始换管脚获取ID复位操作BDU设置设置速率启用偏移消除开启温度补偿设置为连续模式轮询读取数据主程序演示 概述 本文将介绍如何使…...
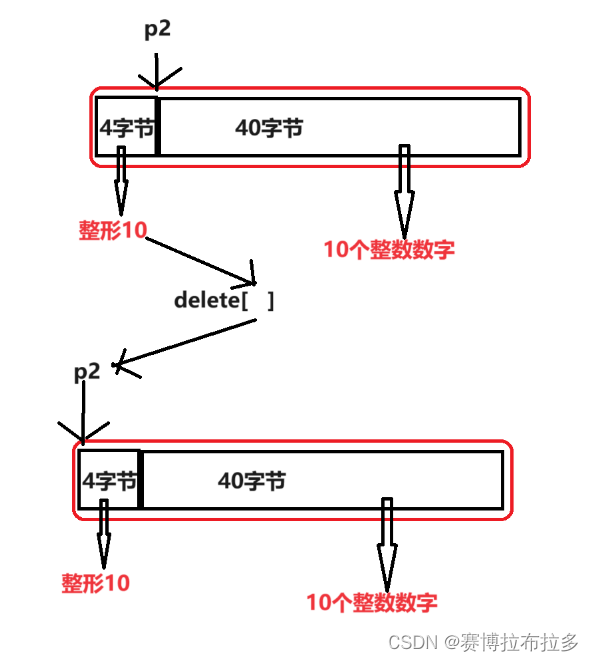
C++学习笔记—— C++内存管理方式:new和delete操作符进行动态内存管理
系列文章目录 http://t.csdnimg.cn/d0MZH 目录 系列文章目录http://t.csdnimg.cn/d0MZH 比喻和理解a.比喻C语言开空间C开空间 b.理解a、C语言的内存管理的缺点1、开发效率低(信息传递繁琐)2、可读性低(信息展示混乱)3、稳定性差&…...
8、操作符重载
友元 可以通过friend关键字,把一个全局函数、另一个类的成员函数或者另一个类整体,声明为授权类的友元友元拥有访问授权类任何非公有成员的特权友元声明可以出现在授权类的公有、私有或者保护等任何区域且不受访问控制限定符的约束友元不是成员…...
前端组件库开发
通常我们会使用很多组件库,有时候我们会去看源码比如element,antd,然后发现多少是按需导出,和vue.use全局注册,依赖于框架的拓展。 组件库的开发依赖框架的版本和node的版本,这个是需要说明的,然…...

自定义日志打印功能--C++
一、介绍 日志是计算机程序中用于记录运行时事件和状态的重要工具。通过记录关键信息和错误情况,日志可以帮助程序开发人员和维护人员追踪程序的执行过程,排查问题和改进性能。 在软件开发中,日志通常记录如下类型的信息: 事件信…...
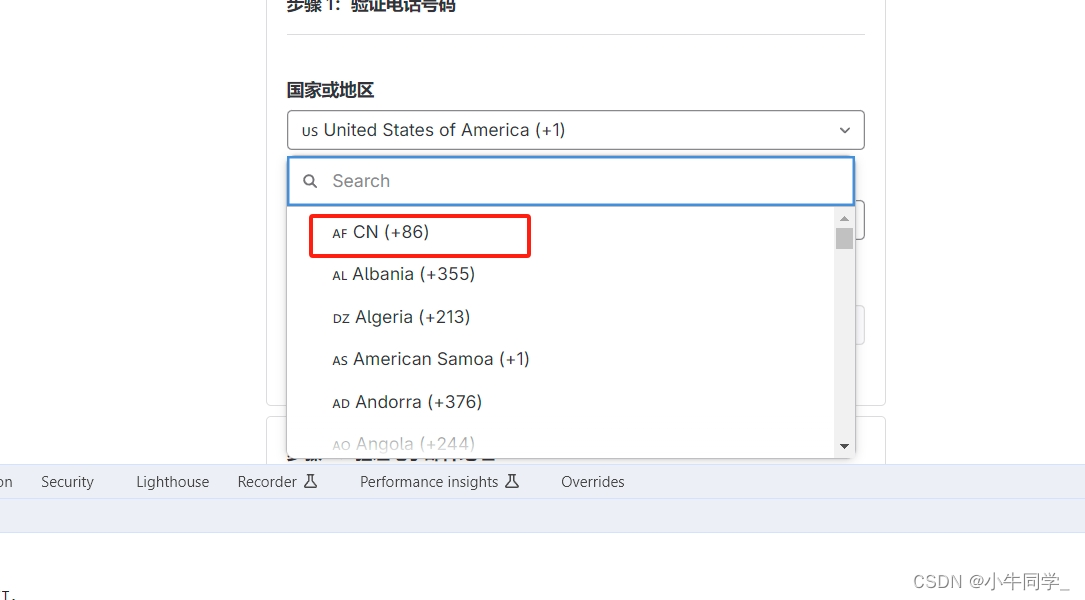
gitlab注册无中国区电话验证问题
众所周知gitlab对中国区不友好,无法直接注册,页面无法选择86的手机号进行验证码发送。 Google上众多的方案是修改dom,而且时间大约是21年以前。 修改dom,对于现在的VUE、React框架来说是没有用的,所以不用尝试。 直接看…...

【JAVA基础题目练习】----第二天
JAVA基础题目练习 1. 键盘录入数据,比较大小2. 代码重构(简化代码,少做判断)3. 键盘录入月份的值,输出对应的季节4. 获取三个数据中的最大值使用IF语句5. 用switch语句实现键盘录入月份,输出对应的季节6. 求…...
node.js和npm的安装与环境配置(2023最新版)
目录 安装node.js测试是否安装成功测试npm环境配置更改环境变量新建系统变量 安装node.js 1、进入官网下载:node.js官网 我选择的是windows64位的,你可以根据自己的实际情况选择对应的版本。 2、下载完成,安装。 打开安装程序 接受协议 选…...

ke14--10章-1数据库JDBC介绍
注册数据库(两种方式),获取连接,通过Connection对象获取Statement对象,使用Statement执行SQL语句。操作ResultSet结果集 ,回收数据库资源. 需要语句: 1Class.forName("DriverName");2Connection conn DriverManager.getConnection(String url, String user, String…...
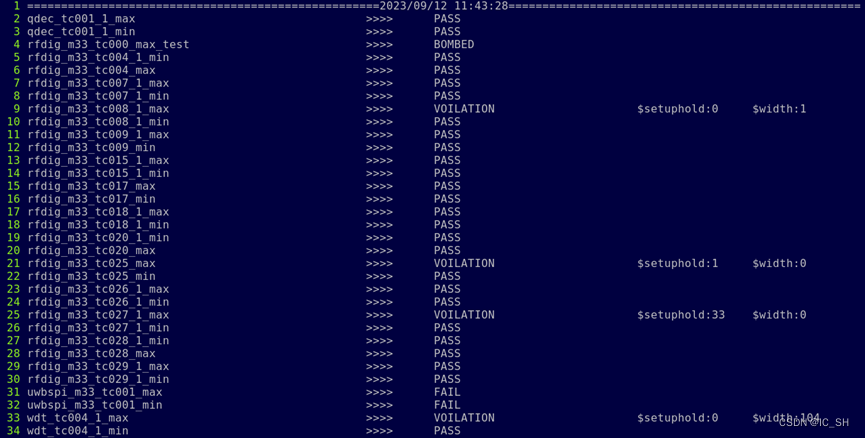
【IC验证】perl脚本——分析前/后仿用例回归情况
目录 1 脚本名称 2 脚本使用说明 3 nocare_list文件示例 4 脚本执行方法 5 postsim_result.log文件示例 6 脚本代码 1 脚本名称 post_analysis 2 脚本使用说明 help:打印脚本说明信息 命令:post_analysis help 前/后仿结束后,首先填…...

Ansible适合的场景是什么?
Ansible将编排与配置管理、供应和应用程序部署结合并统一在一个易于使用的平台上。Ansible的一些主要场景包括: 配置管理:集中配置文件管理和部署是Ansible的一个常见场景。 应用程序部署:当使用Ansible定义应用程序,并使用Ansible Tower管…...

Flink 读写 HBase 总结
前言 总结 Flink 读写 HBase 版本 Flink 1.15.4HBase 2.0.2Hudi 0.13.0官方文档 https://nightlies.apache.org/flink/flink-docs-release-1.17/zh/docs/connectors/table/hbase/ Jar包 https://repo1.maven.org/maven2/org/apache/flink/flink-sql-connector-hbase-2.2/1…...
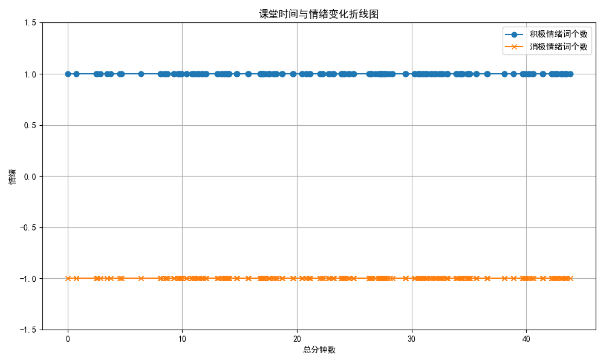
记录一次chatGPT人机协同实战辅助科研——根据词库自动进行情感分析
有一个Excel中的一列,读取文本判断文本包含积极情感词.txt和消极情感词.txt的个数,分别生成两列统计数据 请将 ‘your_file.xlsx’ 替换为你的Excel文件名,Your Text Column’替换为包含文本的列名。 这个程序首先读取了积极和消极情感词&…...
Java_LinkedList链表详解
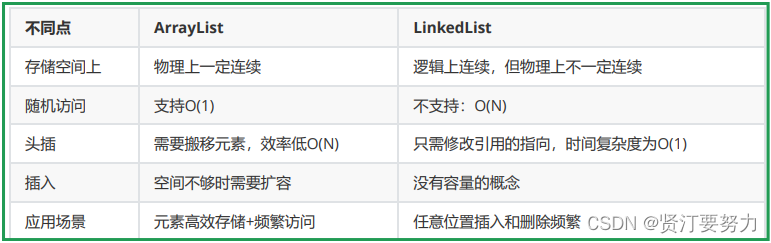
目录 前言 ArrayList的缺陷 链表 链表的概念及结构 链表的种类 1.单向或双向 2.带头或不带头 3.循环或不循环 LinkedList的使用 什么是LinkedList LinkedList的使用 LinkedList的构造 LinkedList的其他常用方法介绍 LinkedList的遍历 ArrayList和LinkedList的…...
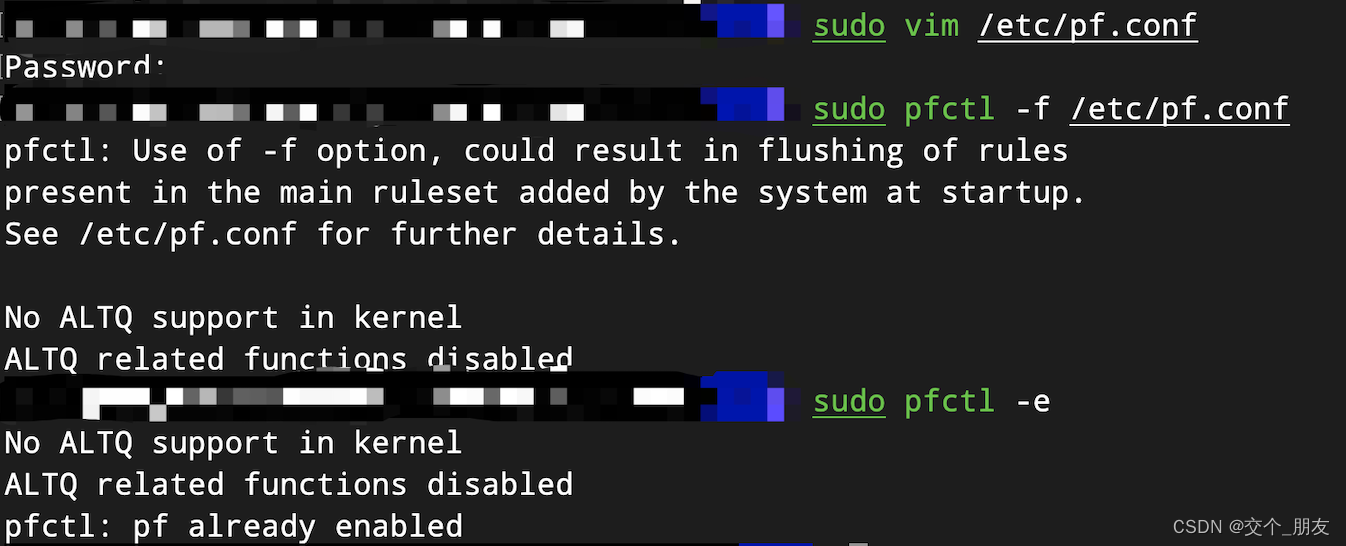
MacOS 12 开放指定端口 指定ip访问
MacOS 12 开放指定端口 指定ip访问 在 macOS 上开放一个端口,并指定只能特定的 IP 访问,你可以使用 macOS 内置的 pfctl(Packet Filter)工具来实现。 以下是一些基本的步骤: 1、 编辑 pf 配置文件: 打开 /…...

LeedCode刷题---滑动窗口问题
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、长度最小的子数组 题目链接:长度最小的子数组 题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。…...

leetcode24. 两两交换链表中的节点
题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:head [1,2,3,4] 输出&#…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
