机器学习-SVM(支持向量机)
推荐课程:【机器学习实战】第5期 支持向量机 |数据分析|机器学习|算法|菊安酱_哔哩哔哩_bilibili
赞美菊神ヾ ( ゜ⅴ゜)ノ
一、什么是支持向量机?
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面(maximum-margin hyperplane)。
1.1 举个例子

在桌子上似乎有规律地放了两种颜色的球,要求你用一根棍子分离开他们,并且尽量再放更多的球之后,仍然适用。

SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙(这被认为是最佳求解)。

并且,现在即使再放入更多的球,棍子仍然是一个很好的分界线。

但是,现在增加难度,如果将球散乱地放在桌子上,又该怎样进行划分呢?很明显,此时在二维平面中,这变成了一个线性不可分的问题,我们没有方法再用一根棍子将这些球分开了,那么怎么解决这样一个问题呢?

解决方法也很简单,我们可以使用一个核函数,将二维平面中的 '小球' 投影到三维空间,也许就可以在三维空间中,有可能找到这样一个平面将其分隔开来。(可以想象一下,用力拍向桌子,然后桌子上的球就被震到空中,瞬间抓起一张纸,插到两种球的中间。)
(话说,如果3维空间依旧找不到这样一个平面呢?没关系,我继续投四维呀╮(๑•́ ₃•̀๑)╭,总能找到一个维度解决线性不可分的问题。)

可以通过视频,更为直观地感受一下这个过程:支持向量机 SVM在线性不可分情况下进行分类 可视化直观展示 高维空间映射_哔哩哔哩_bilibili
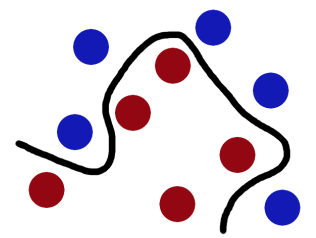
更为规范的,我们把这些球叫做「data」,把棍子叫做「classififier」, 最大间隙 trick 叫做「optimization」,拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。
1.2 概述一下
当一个分类问题,数据是线性可分(linearly separable)的,也就是用一根棍就可以将两种小球分开的时候,我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可,寻找这个最大间隔的过程,就叫做最优化。但是,一般的数据是线性不可分的,也就是找不到一个棍将两种小球很好的类。这个时候,我们就需要使用核函数 (kernel)将小球投影到多维空间(想象一下,将小球拍飞到空中,瞬间抓起一张纸,插到两种球的中间),而在多维空间中切分小球的平面,就是超平面(hyperplane)。如果数据集是N维的,那么超平面就是N-1维的。
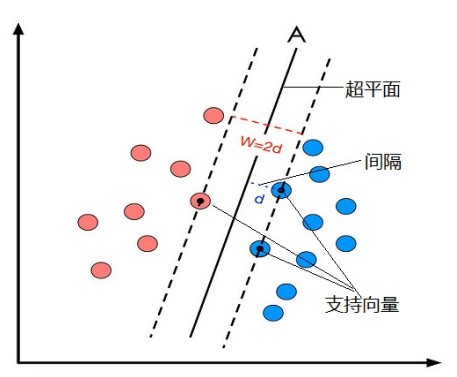
Q:什么是支持向量?
A:把一个数据集正确分开的超平面可能有多个,而那个具有“最大间隔”的超平面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为“支持向量(support vector)”。支持向量到超平面的距离被称为间隔(margin)。
二、线性支持向量机
一个最优化问题通常有两个最基本的因素:
1)目标函数,也就是你希望什么东西的什么指标达到最好;
2)优化对象,你期望通过改变哪些因素来使你的目标函数达到最优。
在线性SVM算法中,目标函数显然就是那个“间隔”,而优化对象则是超平面。
2.1 超平面方程
在线性可分的二分类问题中,超平面其实就是一条直线,公式如下:
![]()
将原来的x轴看作x1轴,y轴看作x2轴,于是公式(1)转换为:

向量形式可以写成:

进一步可表示为:
![]()
其中,![]() ,b为截距。
,b为截距。
2.2 间隔的计算公式
间隔的计算公式 = 点到直线距离推导公式,向量表示法:

其中,是向量
的模,假如
![]() ,则
,则 ![]() ,表示在空间中向量的长度。
,表示在空间中向量的长度。
我们评价分类器的好坏依据是分类间隔的![]() 的大小,即分类间隔W越大,我们认为这个超平面的分类效果越好。而追求分类间隔W的最大化也就是寻找 d的最大化。
的大小,即分类间隔W越大,我们认为这个超平面的分类效果越好。而追求分类间隔W的最大化也就是寻找 d的最大化。
2.3 约束条件
对于SVM的线性可分的二分类问题,我们希望:
1)超平面够将所有的样本点都正确分类。
2)超平面的位置应该是在间隔区域的中轴线上。
3)对于一个给定的超平面,我们能找到对应的支持向量,来计算距离d。

对于上述的三个约束条件,我们假设在平面空间中有红蓝两种点,对其分别标记为:
- 红色为正样本,标记为+1;
- 蓝色为负样本,标记为-1。
对每个样本点 加上类别标签
,则有

如果我们的超平面能够完全将红蓝两种样本点分离开(对应第一个约束条件),那么则有
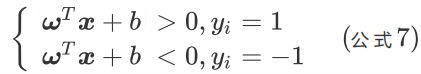
如果要求在再高一点,假设超平面正好处于间隔区域的中轴线上(对应第二个约束条件),并且相应支持向量到超平面的距离为d(对应第三个约束条件),则公式可进一步写为:

对公式两边同时除以d,可得:
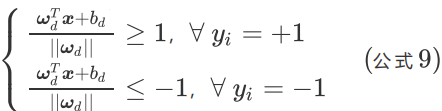
其中,![]() 。
。
简化方程,使用 和
代替
,
,可得:
![]()
当![]() 等于 1或 -1时,对应的
等于 1或 -1时,对应的 坐标就是支持向量的坐标。
以将上述方程糅合成一个约束方程:
![]()
这个方程就是SVM最优化问题的约束条件。
2.4 线性SVM最优化问题
当![]() 等于 1或 -1时,对应的
等于 1或 -1时,对应的 坐标就是支持向量的坐标,相应的根据约束条件,我们可以知道只有超平面最大化时,
![]() 才会等于 1或 -1。无论是等于1还是-1,即
才会等于 1或 -1。无论是等于1还是-1,即 为支持向量坐标时,对于公式10来说,都有
![]() 。
。
所以对于支持向量来说:
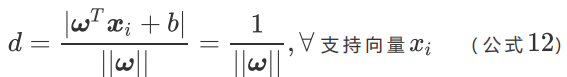
我们原来的任务是找到一组参数 使得分类间隔
最大化,根据公式12 就可以转变为
的最小化问题,也等效于
的最小化问题。我们之所以要在
上加上平方和1/2的系数,是为了以后进行最优化的过程中对目标函数求导时比较方便,但这绝不影响最优化问题最后的解。
所以,线性SVM最优化问题的数学描述就是:

公式13,描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。
2.5 求解线性SVM最优化问题
有不等式约束条件的原始目标函数求解十分困难,我们需要先转化没有约束条件的新目标函数,再进行求导优化,简单来讲过程就是:构造拉格朗日函数 + 求解拉格朗日对偶函数。
最终得到新的目标函数和约束条件,方便使用高效优化算法SMO算法:
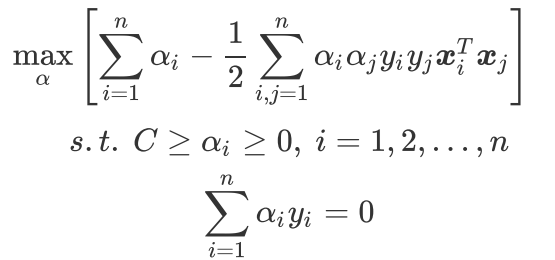
三、SMO算法
SMO算法就是序列最小优化(Sequential Minimal Optimization),它是由 John Platt 于1996年发布的专门用于训练SVM的一个强大算法(如同,梯度下降算法专门用于训练深度学习模型一般)。
简化版SMO算法,如下:
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):"""smoSimpleArgs:dataMatIn 数据集classLabels 类别标签C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。可以通过调节该参数达到不同的结果。toler 容错率(是指在某个体系中能减小一些因素或选择对某个系统产生不稳定的概率。)maxIter 退出前最大的循环次数Returns:b 模型的常量值alphas 拉格朗日乘子"""dataMatrix = mat(dataMatIn)# 矩阵转置 和 .T 一样的功能labelMat = mat(classLabels).transpose()m, n = shape(dataMatrix)# 初始化 b和alphas(alpha有点类似权重值。)b = 0alphas = mat(zeros((m, 1)))# 没有任何alpha改变的情况下遍历数据的次数iter = 0while (iter < maxIter):# w = calcWs(alphas, dataMatIn, classLabels)# print("w:", w)# 记录alpha是否已经进行优化,每次循环时设为0,然后再对整个集合顺序遍历alphaPairsChanged = 0for i in range(m):# print 'alphas=', alphas# print 'labelMat=', labelMat# print 'multiply(alphas, labelMat)=', multiply(alphas, labelMat)# 我们预测的类别 y = w^Tx[i]+b; 其中因为 w = Σ(1~n) a[n]*lable[n]*x[n]fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b# 预测结果与真实结果比对,计算误差EiEi = fXi - float(labelMat[i])# 约束条件 (KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值)# 0<=alphas[i]<=C,但由于0和C是边界值,我们无法进行优化,因为需要增加一个alphas和降低一个alphas。# 表示发生错误的概率:labelMat[i]*Ei 如果超出了 toler, 才需要优化。至于正负号,我们考虑绝对值就对了。'''# 检验训练样本(xi, yi)是否满足KKT条件yi*f(i) >= 1 and alpha = 0 (outside the boundary)yi*f(i) == 1 and 0<alpha< C (on the boundary)yi*f(i) <= 1 and alpha = C (between the boundary)'''if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):# 如果满足优化的条件,我们就随机选取非i的一个点,进行优化比较j = selectJrand(i, m)# 预测j的结果fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + bEj = fXj - float(labelMat[j])alphaIold = alphas[i].copy()alphaJold = alphas[j].copy()# L和H用于将alphas[j]调整到0-C之间。如果L==H,就不做任何改变,直接执行continue语句# labelMat[i] != labelMat[j] 表示异侧,就相减,否则是同侧,就相加。if (labelMat[i] != labelMat[j]):L = max(0, alphas[j] - alphas[i])H = min(C, C + alphas[j] - alphas[i])else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])# 如果相同,就没发优化了if L == H:print("L==H")continue# eta是alphas[j]的最优修改量,如果eta==0,需要退出for循环的当前迭代过程# 参考《统计学习方法》李航-P125~P128<序列最小最优化算法>eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].Tif eta >= 0:print("eta>=0")continue# 计算出一个新的alphas[j]值alphas[j] -= labelMat[j]*(Ei - Ej)/eta# 并使用辅助函数,以及L和H对其进行调整alphas[j] = clipAlpha(alphas[j], H, L)# 检查alpha[j]是否只是轻微的改变,如果是的话,就退出for循环。if (abs(alphas[j] - alphaJold) < 0.00001):print("j not moving enough")continue# 然后alphas[i]和alphas[j]同样进行改变,虽然改变的大小一样,但是改变的方向正好相反alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])# 在对alpha[i], alpha[j] 进行优化之后,给这两个alpha值设置一个常数b。# w= Σ[1~n] ai*yi*xi => b = yj- Σ[1~n] ai*yi(xi*xj)# 所以: b1 - b = (y1-y) - Σ[1~n] yi*(a1-a)*(xi*x1)# 为什么减2遍? 因为是 减去Σ[1~n],正好2个变量i和j,所以减2遍b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].Tb2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].Tif (0 < alphas[i]) and (C > alphas[i]):b = b1elif (0 < alphas[j]) and (C > alphas[j]):b = b2else:b = (b1 + b2)/2.0alphaPairsChanged += 1print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))# 在for循环外,检查alpha值是否做了更新,如果在更新则将iter设为0后继续运行程序# 知道更新完毕后,iter次循环无变化,才推出循环。if (alphaPairsChanged == 0):iter += 1else:iter = 0print("iteration number: %d" % iter)return b, alphas查看代码运行时间及结果:
# 惩罚因子C = 0.6
# 容错率toler = 0.001
# 退出前最大循环次数maxIter=40
%time b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)相关文章:
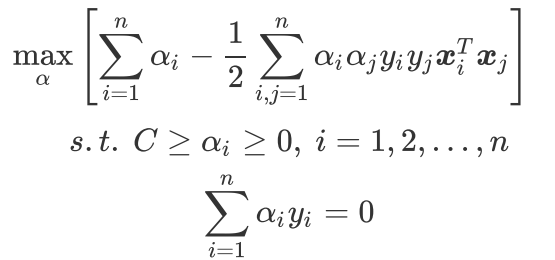
机器学习-SVM(支持向量机)
推荐课程:【机器学习实战】第5期 支持向量机 |数据分析|机器学习|算法|菊安酱_哔哩哔哩_bilibili 赞美菊神ヾ ( ゜ⅴ゜)ノ 一、什么是支持向量机? 支持向量机(Support Vector Machine, SVM)是一类按监督学习࿰…...
保姆级:Windows Server 2012上安装.NET Framework 3.5
📚📚 🏅我是默,一个在CSDN分享笔记的博主。📚📚 🌟在这里,我要推荐给大家我的专栏《Windows》。🎯🎯 🚀无论你是编程小白,还是有…...
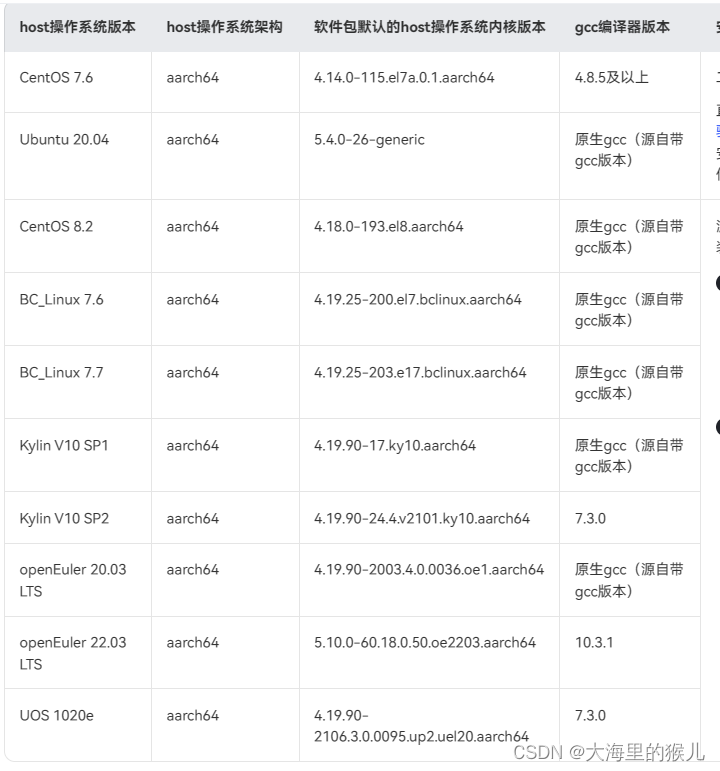
昇腾910安装驱动出错,降低Centos7.6的内核版本
零、问题描述: 在安装Atlas800-9000服务器的驱动的时候,可能会出现错误:Dkms install failed, details in : /var/log/ascend_seclog/ascend_install.log 如下所示: [rootlocalhost ~]# ./Ascend-hdk-910-npu-driver_23.0.rc3_l…...

LeetCode刷题日志-73矩阵置零
思路一: 用一个同样大小的矩阵记录0的位置,然后遍历矩阵置0, 空间复杂度为O(mn) class Solution {public void setZeroes(int[][] matrix) {int [][] matrix_new new int[matrix.length][matrix[0].length];for(int …...

基于Python+WaveNet+MFCC+Tensorflow智能方言分类—深度学习算法应用(含全部工程源码)(四)
目录 前言引言总体设计系统整体结构图系统流程图 运行环境模块实现1. 数据预处理2. 模型构建3. 模型训练及保存4. 模型生成 系统测试1. 训练准确率2. 测试效果 相关其它博客工程源代码下载其它资料下载 前言 博主前段时间发布了一篇有关方言识别和分类模型训练的博客ÿ…...
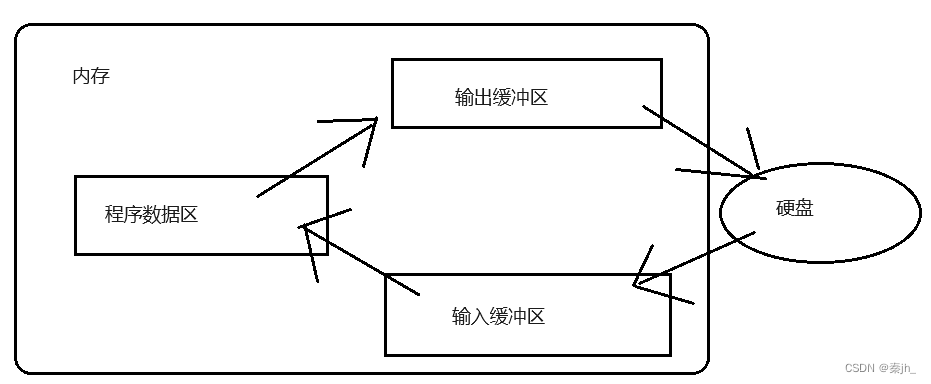
文件操作及函数
什么是文件? 在程序设计中,文件有两种:程序文件和数据文件。 程序文件 包括源程序文件(.c),目标文件(.obj),可执行程序(.exe)。 数据文件 文件的内容不一定是程序&…...
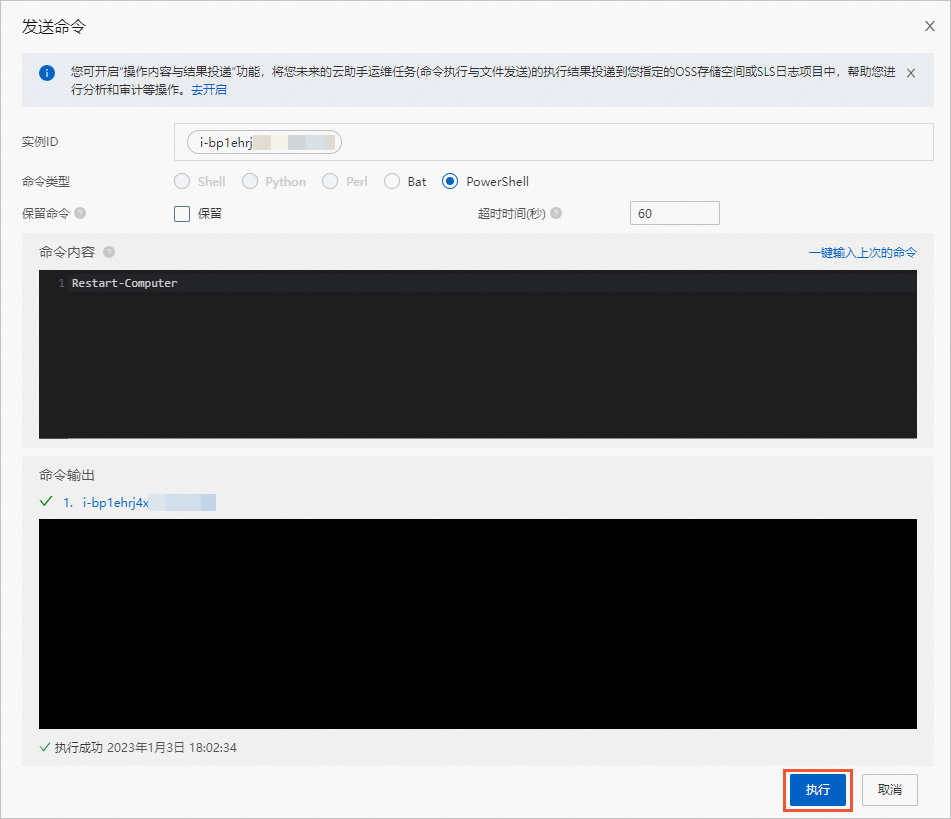
阿里云国际版无法远程连接Windows服务器的排查方法
如果您遇到紧急情况,需要尽快登录Windows实例,请参见以下操作步骤,先检查ECS实例的状态,然后通过云助手向Windows实例发送命令或通过VNC登录实例,具体步骤如下: 步骤一:检查ECS实例状态 无论何…...
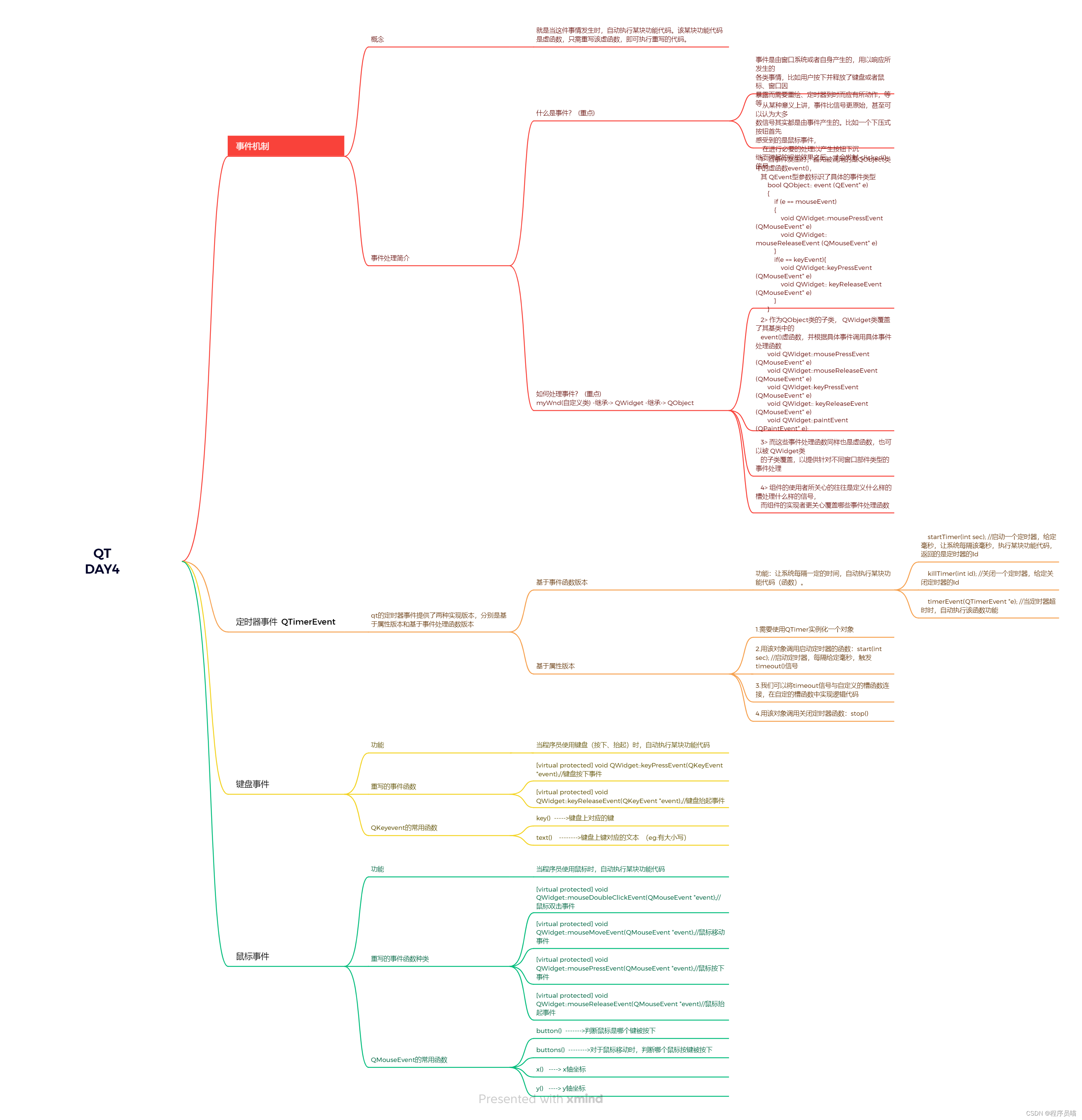
华清远见嵌入式学习——QT——作业4
作业要求: 代码运行效果图: 代码: 头文件: #ifndef ALARMCLOCK_H #define ALARMCLOCK_H#include <QWidget> #include <QTimerEvent> #include <QTimer> #include <QTime> #include <QTextToSpeech&g…...

Visuial Studio 打开 Unity 脚本时,脚本继承MonoBehaviour暂时失效为白色的解决方法
问题描述: u3d2020.3.47f1c1 vs2019 之前C#脚本A好好的,今天改了一行代码,在储存,就出现这个问题了,变白之后,新增的一行代码不生效,之前的代码照常运行。 如下办法都不能解决我的问题&…...

CentOS使用kkFileView实现在线预览word excel pdf等
一、环境安装 1、安装LibreOffice wget https://downloadarchive.documentfoundation.org/libreoffice/old/7.5.3.2/rpm/x86_64/LibreOffice_7.5.3.2_Linux_x86-64_rpm.tar.gz # 解压缩 tar -zxf LibreOffice_7.5.3.2_Linux_x86-64_rpm.tar cd LibreOffice_7.5.3.2_Linux_x86…...

黑豹程序员-EasyExcel实现导出
需求 将业务数据导出到excel中,老牌的可以选择POI,也有个新的选择EasyExcel。 有个小坑,客户要求样式比较美观,数字列要求千位符,保留2位小数。 可以用代码实现但非常繁琐,用模板就特别方便,模…...

【项目小结】优点分析
一、 个人博客系统 一)限制强制登录 问题:限制用户登录后才能进行相关操作解决: 1)前端: ① 写一个函数用于判断登录状态,如果返回的状态码是200就不进行任何操作,否则Ajax实现页面的跳转操作…...
已经写完的论文怎么降低查重率 papergpt
大家好,今天来聊聊已经写完的论文怎么降低查重率,希望能给大家提供一点参考。 以下是针对论文重复率高的情况,提供一些修改建议和技巧: 已经写完的论文怎么降低查重率 背景介绍 在学术界,论文的查重率是评价论文质量的…...
科研论文中PPT图片格式选择与转换:EPS、SVG 和 PDF 的比较
当涉及论文中的图片格式时,导师可能要求使用 EPS 格式的图片。EPS(Encapsulated PostScript)是一种矢量图格式,它以 PostScript 语言描述图像,能够无损地缩放并保持图像清晰度。与像素图像格式(如 PNG 和 J…...

mybatis xml 热部署
平时我们在项目中多多少少会根据不同的情况等等原因去调试sql,在数据库测试完后也需要在代码里面运行测试,但是每次修改就需要重启服务就显得太繁琐,所以如果mybatis的xml也可以热部署当然是最好的了,那我来试试如何可以将mybatis…...
MySQL的事务以及springboot中如何使用事务
事务的四大特性: 概念: 事务 是一组操作的集合,它是不可分割的工作单元。事务会把所有操作作为一个整体,一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 注意: 默认MySQ…...

docker二 redis单机安装
创建文件夹 mkdir -p /usr/local/redis/data /usr/local/redis/logs /usr/local/redis/conf chmod -R 777 /usr/local/redis/data* chmod -R 777 /usr/local/redis/logs*另一种风格 # 创建 redis 配置存放目录 mkdir -p /home/docker/redis/conf && chmod 777 /home/…...
【解决】Vue elementUI table表格 列错位/滑动后切换每页显示数后错位/表格使用fixed后错位...
table表格右侧列固定后,在切换页面之后,就会出现列错误的现象 <el-tablev-adaptive"{ bottomOffset: 85 }"height"100px"v-loading"loading":data"dataList"> 解决方法 方法一 1、给表格添加ref &…...

uniapp实战 —— 分类导航【详解】
效果预览 组件封装 src\pages\index\components\CategoryPanel.vue <script setup lang"ts"> import type { CategoryItem } from /types/index defineProps<{list: CategoryItem[] }>() </script><template><view class"category&…...

LangChain学习二:提示-实战(下半部分)
文章目录 上一节内容:LangChain学习二:提示-实战(上半部分)学习目标:提示词中的示例选择器和输出解释器学习内容一:示例选择器1.1 LangChain自定义示例选择器1.2 实现自定义示例选择器1.2.1实战:…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

