什么是泊松图像混合

泊松图像混合(Poisson Image Editing)的原理基于泊松方程。该方法旨在保持图像中的梯度一致性,从而在图像编辑中实现平滑和无缝的混合。以下是泊松图像混合的基本原理和公式:
泊松方程
泊松方程是一个偏微分方程,通常用于描述物理和数学中的一些现象。在图像处理中,泊松方程的形式如下:
[\nabla^2 u = f]
其中,(\nabla^2) 是拉普拉斯算子,(u) 是图像中的像素值,(f) 是输入图像中的梯度。
泊松图像混合
在图像编辑中,泊松图像混合的目标是将源图像 (S) 中的内容(包含一些掩码区域)融合到目标图像 (T) 中。设混合结果为 (R)。
-
定义泊松方程
泊松图像混合的目标是找到一个图像 (R),使得在掩码区域内,(R) 的梯度与源图像 (S) 中的梯度相匹配,并且在掩码区域外,(R) 等于目标图像 (T)。
[\nabla^2 R = \nabla^2 S \quad \text{在掩码区域内}]
[R = T \quad \text{在掩码区域外}] -
离散化泊松方程
将泊松方程离散化,得到以下方程:
[4R_{i,j} - R_{i-1,j} - R_{i+1,j} - R_{i,j-1} - R_{i,j+1} = S_{i,j} \quad \text{在掩码区域内}]
[R_{i,j} = T_{i,j} \quad \text{在掩码区域外}]其中,(R_{i,j}) 是混合图像中像素 ((i,j)) 处的值,(S_{i,j}) 是源图像中像素 ((i,j)) 处的值,(T_{i,j}) 是目标图像中像素 ((i,j)) 处的值。
-
求解泊松方程
这是一个线性方程组,可以通过迭代求解、矩阵求逆等方法来得到混合图像 (R)。
在实际应用中,为了更好地处理边界和获得高质量的混合结果,通常会采用一些改进的算法,如高斯-赛德尔方法、共轭梯度法等。
请注意,上述是泊松图像混合的基本思想和公式,实际实现可能涉及到更多的细节和优化。希望这能帮助理解泊松图像混合的原理。
相关文章:

什么是泊松图像混合
泊松图像混合(Poisson Image Editing)的原理基于泊松方程。该方法旨在保持图像中的梯度一致性,从而在图像编辑中实现平滑和无缝的混合。以下是泊松图像混合的基本原理和公式: 泊松方程 泊松方程是一个偏微分方程,通常…...

OpenAI 承认 ChatGPT 最近确实变懒,承诺修复问题
文章目录 一. ChatGPT 指令遵循能力下降引发用户投诉1.1 用户抱怨回应速度慢、敷衍回答、拒绝回答和中断会话 二. OpenAI 官方确认 ChatGPT 存在问题,展开调查三. OpenAI 解释模型行为差异,回应用户质疑四. GPT-4 模型变更受人事动荡和延期影响 一. Chat…...
———低代码:美味膳食或垃圾食品?)
创作活动(四十九)———低代码:美味膳食或垃圾食品?
#低代码:美味膳食或垃圾食品?# 一、什么是低代码 低代码是一种开发方法,通过可视化界面和少量的编码,使开发者能够快速构建应用程序。它的目标是提高开发效率、降低开发成本,并支持快速迭代和敏捷开发。 二、低代码的…...

【DL-TensorFlow遇错】TensorFlow中遇错合集
TensorFlow中遇错合集 一、AttributeError: module tensorflow has no attribute placeholder二、RuntimeError: tf.placeholder() is not compatible with eager execution. 一、AttributeError: module tensorflow has no attribute placeholder 错误原因 tensorflow版本问…...

pymysql代替mysqlclient,解决mysqlclient因版本不兼容无法安装成功而无法连接mysql的问题
pymysql代替mysqlclient,解决mysqlclient因版本不兼容无法安装成功而无法连接mysql的问题 原因:版本或者环境兼容问题,导致如centos或者其他Linux无法安装mysqlclient模块 解决办法:安装pymysql作为替代 在Django中连接MySQL数…...
uni-app 设置当前page界面进入直接变为横屏模式
首先 我们打开项目的 manifest.json 在左侧导航栏中找到 源码视图 然后找到 app-plus 配置 在下面加上 "orientation": [//竖屏正方向"portrait-primary",//竖屏反方向"portrait-secondary",//横屏正方向"landscape-primary",//横屏…...

Mysql的多表联合查询
内连接 隐式内连接 select column from tb1,tb2 where 条件; 显示内连接 关键字:[inner] join on 显示内连接与外连接的不同是新增的关键字,inner join 以及 使用on 替换了where select column from tb1 [inner] join tb2 on 条件; 外连接 左外…...

Linux上使用Python的requests库进行HTTP请求
在Linux上使用Python的requests库进行HTTP请求是一种非常方便和高效的方式。requests库是一个第三方库,用于发送HTTP请求并获取响应。下面是一个简单的示例,演示如何使用requests库发送GET请求并获取响应。 首先,你需要安装requests库。你可…...

图像处理领域的应用
图像处理领域的应用 文章目录 图像处理领域的应用1.图像类型2.图像转换3.彩色图像表示模式4.图像变换5.图像增强 1.图像类型 #mermaid-svg-x6mNS3Y1YkPvWUsQ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-x6mNS3Y1…...
MySQL笔记-第18章_MySQL8其它新特性
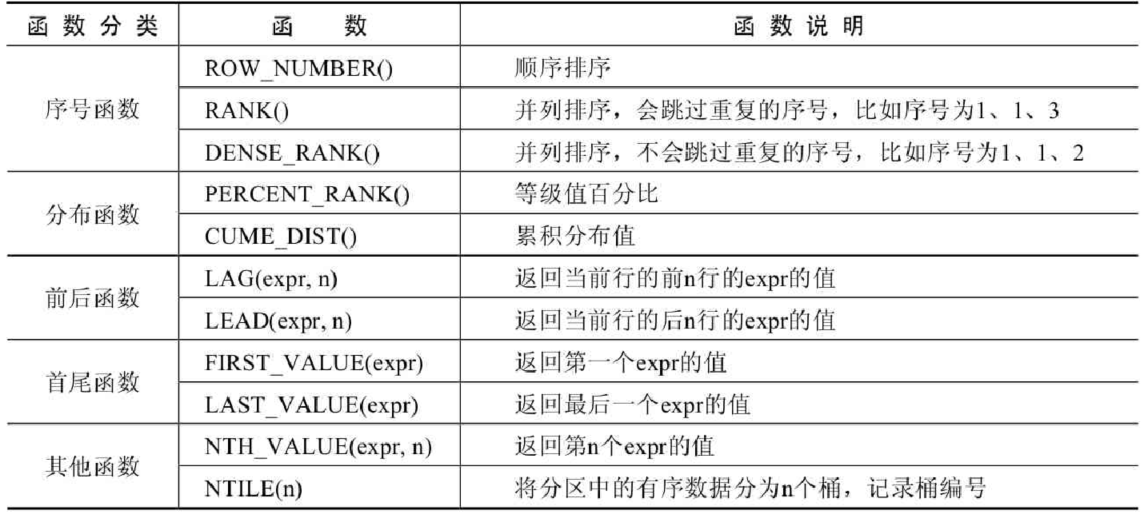
视频链接:【MySQL数据库入门到大牛,mysql安装到优化,百科全书级,全网天花板】 文章目录 第18章_MySQL8其它新特性1. MySQL8新特性概述1.1 MySQL8.0 新增特性1.2 MySQL8.0移除的旧特性 2. 新特性1:窗口函数2.1 使用窗口…...
C语言—每日选择题—Day46
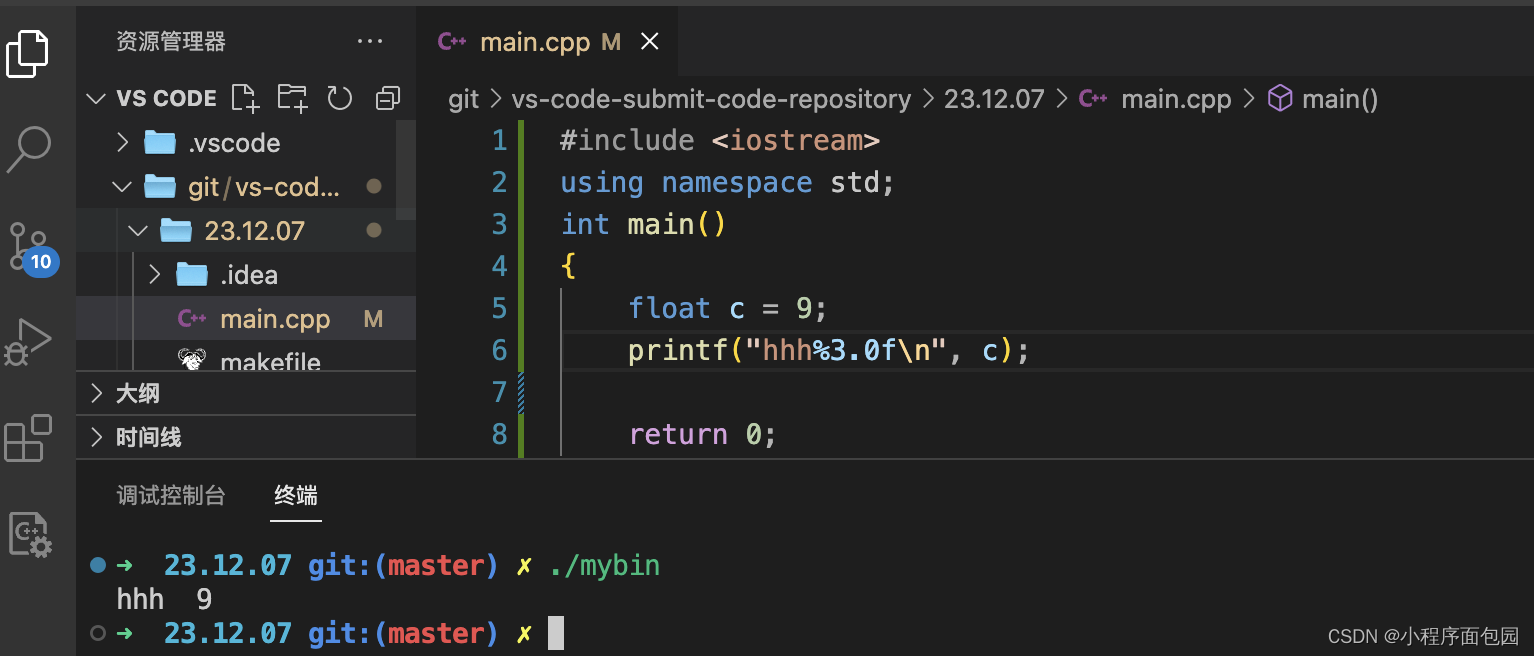
第一题 1. 下列程序段的输出结果是() #include <stdio.h> int main() {int x 1,a 0,b 0;switch(x) {case 0: b;case 1: a;case 2: a;b;}printf("a%d,b%d\n", a, b);return 0; } A:a2,b1 B:a1,b1 C…...

flex布局,换行的元素上下设置间距
要生成的效果图如下: display:flexflex-direction: row;flex-wrap: wrap;当我们使用弹性盒子布局后,默认元素是没有外边距的,紧挨着样式就有点丑,如果想使换行后,元素的外边距有个距离,可以用如下方法解决…...
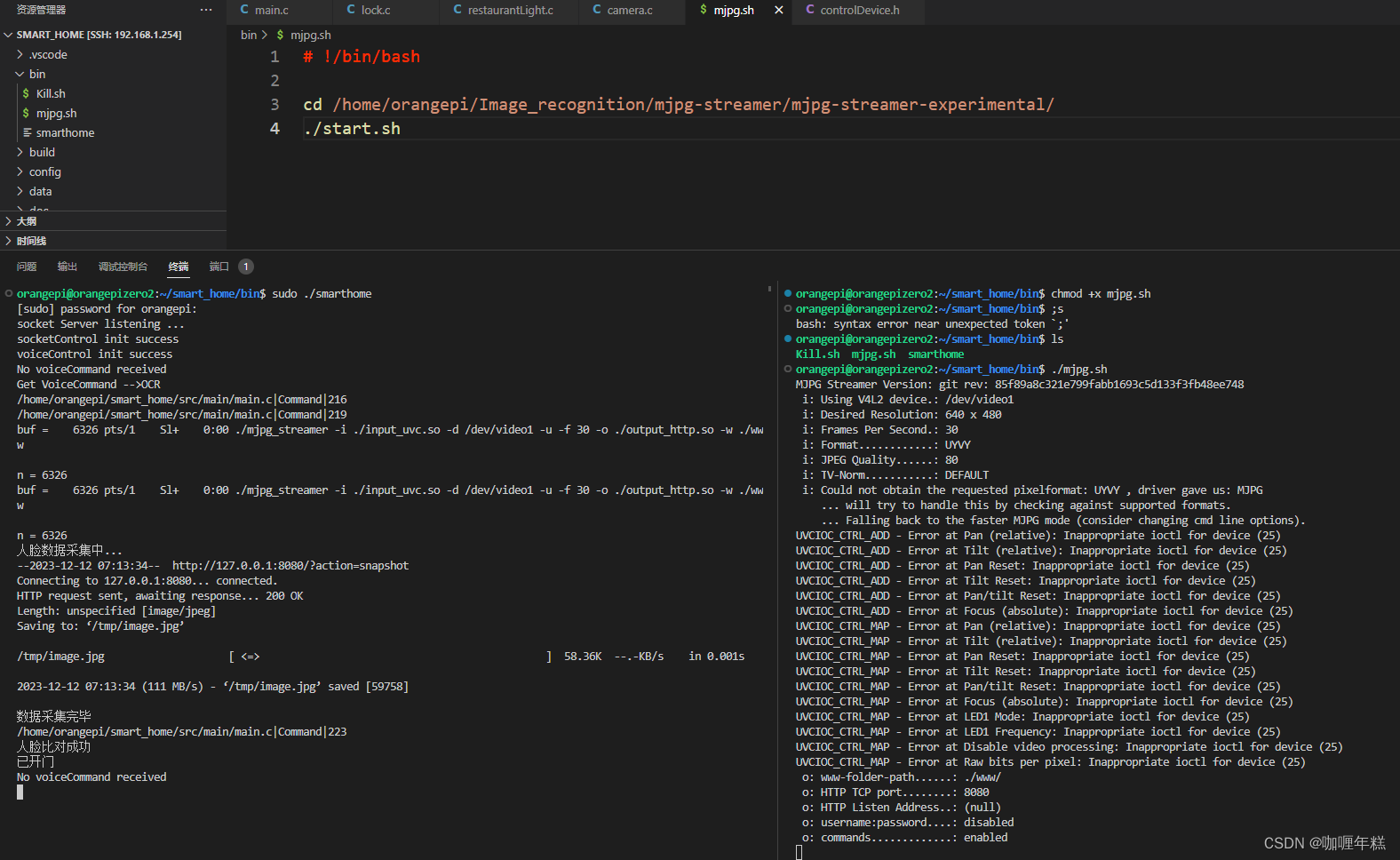
【智能家居】八、监控摄像采集、人脸识别比对进行开门功能点
一、使用 fswebcam 测试 USB 摄像头 二、根据demo来实现功能点 三、功能点编写编译运行实现 四、mjpg实现监控识别 五、V4L2 视频设备 Linux 内核模块的一部分 一、使用 fswebcam 测试 USB 摄像头 a. 安装 fswebcam orangepiorangepi:~$ sudo apt update orangepiorangepi:~…...

golang的文件操作
获取文件列表路径 package _caseimport ("fmt""log""os""strings" )// 获取文件路径 // 源文件目录 const sourceDir "file/"// 目标文件目录 const destDir "det_file/"// 拿到目录下完整的路径 func geFiles…...

数据库版本管理框架-Flyway(从入门到精通)
一、flyway简介 Flyway是一个简单开源数据库版本控制器(约定大于配置),主要提供migrate、clean、info、validate、baseline、repair等命令。它支持SQL(PL/SQL、T-SQL)方式和Java方式,支持命令行客户端等&am…...

外网访问内网服务器使用教程
如何在任何地方都能访问自己家里的笔记本上的应用?如何让局域网的服务器可以被任何地方访问到?有很多类似的需求,我们可以统一用一个解决方案:内网穿透。内网穿透的工具及方式有很多,如Ngrok、Ssh、autossh、Natapp、F…...

C# Dictionary 利用 ContainsValue 查询指定值是否已经存在
.NET Framework : 4.7.2IDE : Visual Studio Community 2022OS : Windows 10 x64typesetting : Markdownblog : niaoge.blog.csdn.net 简介 本文介绍如何查询Dictionary 中某个值是否已经存在。 ContainsValue 命名空间: System.Collections.Generic 程序集: System.Collect…...

招不到人?用C语言采集系统批量采集简历
虽说现在大环境不太好,很多人面临着失业再就业风险,包括企业则面临着招人人,找对口专业难得问题。想要找到适合自己公司的人员,还要得通过爬虫获取筛选简历才能从茫茫人海中找到公司得力干将。废话不多说,直接开整。 1…...
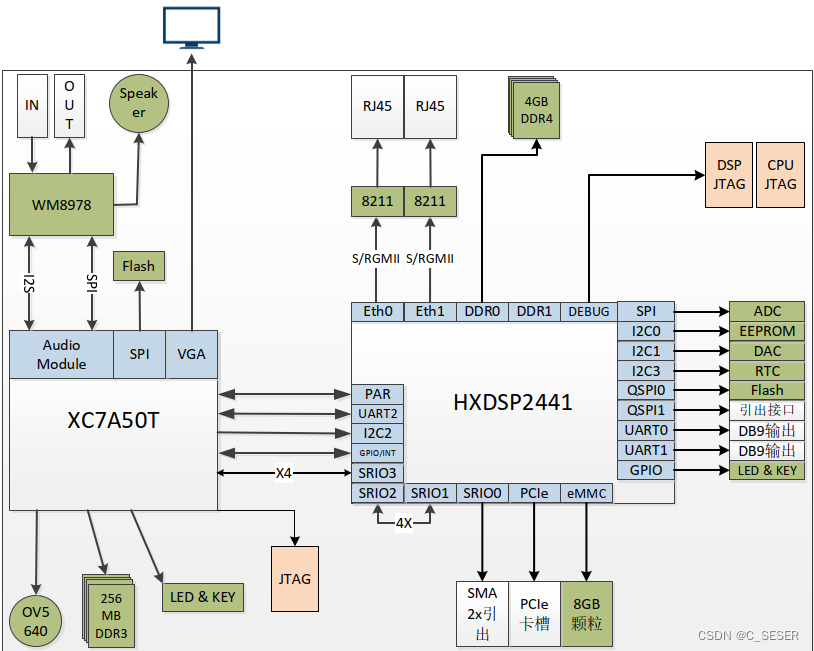
HXDSP2441-Demo板
板卡图示 下图为HXDSP2441DEMO板,HXDSP2441DEMO板是围绕HXDSP2441构建的芯片演示验证平台。 板卡简介 除了为HXDSP2441芯片提供供电、时钟、储存、网络及调试电路,来实现芯片最基本的功能,也添加了相关模块以搭建HXDSP2441的典型应用场景…...
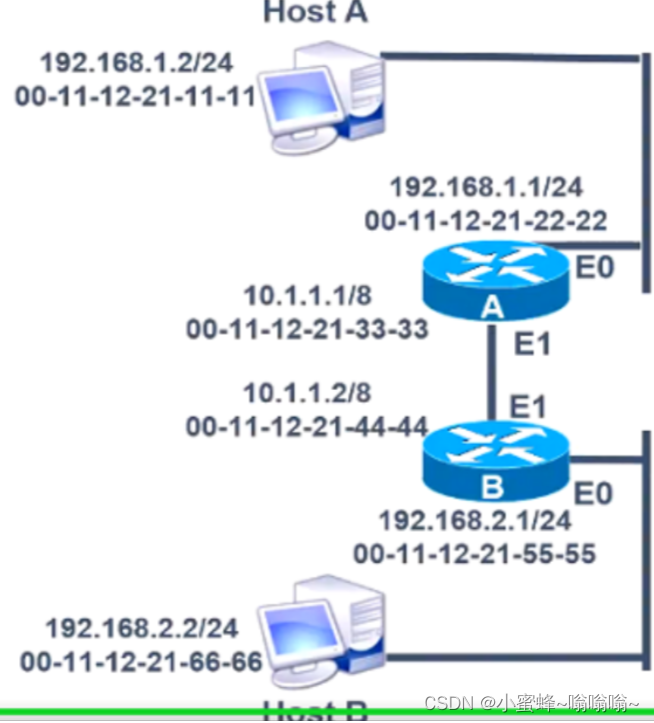
静态路由的原理和配置
一.路由器的工作原理 首先我们知道路由器是工作在网络层的,那就是三层设备。网络层的功能主要为:不同网段之间通信、最佳路径选择也就是逻辑地址(ip地址)寻址、转发数据。 1.路由器是什么 路由器是能将数据包转发到正确的目的地…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
