电线电缆行业生产管理MES系统解决方案
电线电缆行业生产管理mes系统核心功能
基础数据管理:对基础数据进行统一管理,包括组织架构、原材料数据、设备数据、报工数据、检验数据、员工数据等
工艺与BOM管理:对工艺标准进行统一管理,包括工艺的版本管理、关联型号管理,同时对PBOM、MBOM进行版本与分组管理,便于适应不同场景,并具备查询功能
生产排产管理:根据订单优先级,交货期,以及设备、原材料、人员、库存等约束条件,系统自动计算当前条件下最优排程方案,一键下发生产计划
报价管理:批量导入用户询价列表,自动计算材料成本、利率、销售价等,可自动调节材料单价,并且具备防错机制,可导出报价单
生产报工管理:员工可自行查看生产任务,生产完成后,员工点击完工,结束操作,汇报任务,更新订单生产进度等,管理层也可随时随地在设备上或移动端查看任务完成情况
质量检验管理:原材料检验、导体检验、抽检等数据进行记录,质检管理具备异常处理流程,最终能够实现质量信息的完整追溯,对不合格品进行严格把控,能够生成出厂报告与合格证
设备管理:建立设备统一台账,根据设备实际情况制定点检和保养计划,减小设备发生故障的几率,通过自动采集、扫码等方式直接获取设备数据,减少人工录入或耗费在非必要操作上的时间
仓储物流管理:对原材料仓、半成品仓、工装磨具仓、电线电缆成品仓进行统一的透明化管理,严格规范入库、出库、移库、盘点、拣选与物流等操作流程,实现仓储物流管理精准化
万界星空科技电线电缆行业低代码云MES系统应用价值
1、计划制定效率全面提升
结合电缆行业特性(如工序间流转多样性,工序之间的节拍差异)建立模型算法,贴合企业特征;利用算法提高排产效率,单次排产耗时从1天提升至15分钟,并提供排产模拟、产能预测等功能,有效提升计划的合理性。
2、产品报价快速精准
批量导入客户询价列表,自动计算材料成本,利率,销售价等;并且可以结合最新材料单价来手动进行调节,同时具备优惠价计算功能,如超过销售权限则启动审批流程,系统报价功能操作简单,不但具备防错机制,还可导出报价单,可大幅提升报价部门的工作效率,满足客户快速要价的需求。
3、设备利用率明显提升
系统根据设备实际情况制定全面的点检和保养计划,通过对计划的执行使设备时刻处于健康状态,最大程度上减小设备发生故障的几率,从而降低设备因故而被迫停机的时间。同时对设备进行集中线上管理,通过自动采集、扫码等方式直接获取设备数据信息,减少人工录入或耗费在非必要操作上的时间。
4、实现生产全透明化管理
由于电缆产品的特殊性,因此生产车间占地面积较大,设备也很多,为了便于管理,会通过设置车间大屏看板,让现场管理人员可以对生产情况一目了然,也可以让高层领导不下现场,通过PC、手机、平板等移动设备,就能随时随地掌控订单达成率、产量、合格率、设备状态、库存等关键指标,实现工厂的透明化管理
5、仓储物流全面信息化
对所有原材料、半成品、成品、工装磨具等划分仓库进行统一管理,通过仓库、库区、库位进行标准化放置,并借助二维码进行管理,入库、领用、归还、报废、出库等都必须通过系统进行操作,避免仓库管理混乱;在物流环节,发货组员工根据备货单指定的仓位、单号进行取货备货和装车,同时出库单匹配司机信息,以及物流信息登记。

上海万界星空科技有限公司专注提供AI低代码云MES系统,AR数字孪生,商业开源Mes等软件系统定制部署及服务。我们提供给客户的不单单是一个软件、更是根据客户企业情况制定不同的企业管理流程,制定适合企业的信息化方案,助力企业实现信息化管理,提升效率,提升竞争力.
百度搜索万界星空科技官网免费下载使用:https://www.metaxk.vip
相关文章:

电线电缆行业生产管理MES系统解决方案
电线电缆行业生产管理mes系统核心功能 基础数据管理:对基础数据进行统一管理,包括组织架构、原材料数据、设备数据、报工数据、检验数据、员工数据等工艺与BOM管理:对工艺标准进行统一管理,包括工艺的版本管理、关联型号管理&…...

滑动窗口最大值和前K个高频元素
滑动窗口最大值和前K个高频元素 239. 滑动窗口最大值 核心:建立一个单调队列,维护里面的最大值,并且从大到小的顺序即可!【只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。…...

C语言实现在顺序表中找到最大值
用C语言实现在顺序表中找到最大值: #include <stdio.h> #define MAX_SIZE 100 int findMax(int arr[], int size) { int max arr[0]; // 假设第一个元素为最大值 for (int i 1; i < size; i) { // 从第二个元素开始遍历列表 if (…...

数字工厂管理系统建设层级分为哪几层
随着工业4.0时代的到来,数字工厂已成为制造业转型升级的必经之路。数字工厂管理系统作为数字工厂的核心组成部分,对于提高生产效率、降低成本、提升质量等方面具有重要意义。数字工厂管理系统的建设层级一般分为以下几个层次,本文将对其进行详…...
MySQL 8 update语句更新数据表里边的数据
数据重新补充 这里使用alter table Bookbought.bookuser add userage INT after userphone;为用户表bookuser在userphone列后边添加一个类型为INT的新列userage。 使用alter table Bookbought.bookuser add sex varchar(6) after userage ;为用户表bookuser在userage 列后边添…...
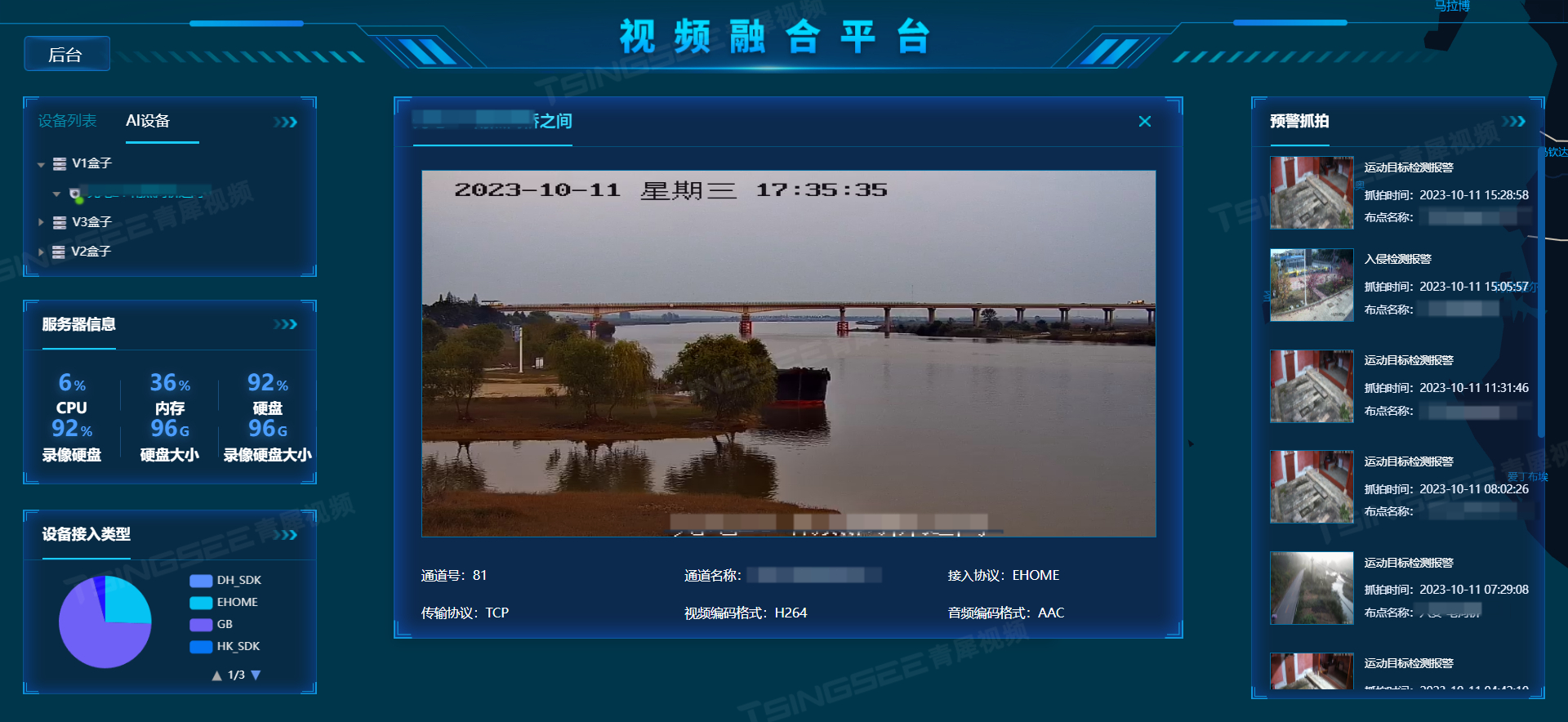
可视化监控云平台/智能监控平台EasyCVR国标设备开启音频没有声音是什么原因?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。GB28181视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存…...
L1-039:古风排版
题目描述 中国的古人写文字,是从右向左竖向排版的。本题就请你编写程序,把一段文字按古风排版。 输入格式: 输入在第一行给出一个正整数N(<100),是每一列的字符数。第二行给出一个长度不超过1000的非空字…...

树莓派新手装机指南
如果你决定买一个树莓派,那么你一定已经了解过,不需要再做多余的介绍,由于之前就玩过树莓派,还是想弄一个属于自己的树莓派,因为它就像一个微型电脑,耗电非常低,我可以在家里24小时开机…...

flink使用事件时间时警惕kafka不同分区的事件时间倾斜问题
背景 flink和kafka的消息组合消费模式几乎是实时流处理的标配,然后当在flink中使用事件时间处理时,需要注意kafka不同分区元素之间时间相差太大的问题,这样有可能会导致严重的数据堆积问题 kafka不同分区元素事件时间差异较大导致的问题 总…...
『App自动化测试之Appium基础篇』| Desired Capabilities详解与使用
App自动化测试之Appium基础篇』| Desired Capabilities详解与使用 1 关于appium driver2 安装appium driver3 安装Appium Python Client4 安装测试对象5 获取测试对象信息5.1 使用dumpsys5.2 使用AndroidKiller5.3 使用aapt 6 Capabilities详解6.1 Capabilities介绍6.2 automat…...

vscode插件webview和插件通信
如果你要在 VS Code 插件的 WebView 中调用插件中的方法,可以使用 vscode.postMessage API。具体步骤如下: 在插件中,在创建 WebView 时,指定一个 onDidReceiveMessage 回调方法,该方法会在 WebView 中调用 vscode.po…...

【STM32单片机】贪吃蛇游戏设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器,使用IIC OLED模块、按键等。 主要功能: 系统运行后,OLED显示游戏界面,可通过K1-K4键控制蛇的方向,当蛇吃…...

【Java 基础】32 定时调度
文章目录 Timer 类创建 Timer注意事项 ScheduledExecutorService 接口创建 ScheduledExecutorService注意事项 选择合适的定时调度方式Timer 的适用场景ScheduledExecutorService 的适用场景 总结 在软件开发中,定时任务是一种常见的需求,用于周期性地执…...

C++ 教程 - 02 复合数据类型
文章目录 数组vector字符串输入输出结构体枚举指针引用综合案例 数组 相同类型的数据的集合{ },通过索引访问元素;在内存中连续存储,属于顺序表;插入、删除时间复杂度 O ( n ) O(n) O(n),访问复杂度 O ( 1 ) O(1) O(1…...

【数据处理】NumPy数组的合并操作,如何将numpy数组进行合并?
,NumPy中的合并操作是指将两个或多个数组合并成一个数组的操作。这种操作可以通过不同的函数来实现。 一、横向合并(水平合并) 横向合并是指将两个具有相同行数的数组按列方向合并成一个数组的操作。在NumPy中,可以使用hstack()…...

JavaScript实现飘窗功能
实现飘窗功能很简单 html代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title…...

Docker笔记:容器转换成镜像,导出导入镜像,数据拷贝,查看日志
docker commit 将容器转换成镜像 可以把容器转换成镜像镜像没有写入权限,但可以通过修改容器把容器制作成新镜像启动容器后,就给容器提供了一个可写层, 在容器里,可安装软件,可创建文件 …转换成镜像,之后…...
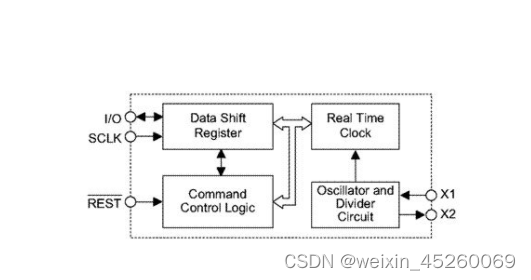
串行计时芯片D1380/D1381,2.0V~5.5V 工作电流: 2V时 与TTL 兼容,采用DIP8、SOP8封装
D1380/D1381是一个带秒、分、时、日、日期、月、年的串行时钟保持芯片,每个月多少天以及闰年能自动调节, D1380/D1381低功耗工作方式, D1380/D1381用若干寄存器存储对应信息,一个32.768kHz 的晶振校准时钟,为了使用最小弓|脚,D1380/D1381使用…...
中间件系列 - Redis入门到实战(基础篇)
前言 1.学习视频: 黑马程序员Redis入门到实战教程,深度透析redis底层原理redis分布式锁企业解决方案黑马点评实战项目 2. 本内容仅用于个人学习笔记,如有侵扰,联系删除 3. 本章学习目标: 初始Redis 认识NoSQL认识Redi…...

项目经理和产品经理该如何选择?
最近很多人咨询“项目经理跟产品经理该怎么选,我更适合哪个?”“项目经理跟产品经理哪个更有钱途 ”“项目经理转产品经理好转吗”等等,今天就一次性说清楚项目经理跟产品经理有什么区别,应该怎么选择。 不想看长篇大论的&#x…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
