蓝桥杯小白赛第一场(1~6)(期望DP)
1、模拟
2、贪心
3、前缀和
4、猜结论
5、双指针
6、期望DP(公式有问题已更改)
1. 蘑菇炸弹

思路:一个简单的暴力模拟。
#include <bits/stdc++.h>
using namespace std;
int main()
{int n;cin >> n;vector<int>a(n , 0);for(int i = 0 ; i < n ; i ++)cin >> a[i];int cnt = 0;for(int i = 1 ; i < n - 1; i ++){if(a[i] >= a[i - 1] + a[i + 1])cnt++;}cout << cnt;return 0;
}2. 构造数字

思路:考虑正整数中每一位的贡献:可以发现位数越大的位置贡献越大,因此将M优先分配给高位即可。
#include <bits/stdc++.h>
using namespace std;
int main()
{int n , m;cin >> n >> m;for(int i = 0 ; i < n ; i ++){int x = min(m , 9);cout << x;m -= x;}return 0;
}3. 小蓝的金牌梦

思路: 首先考虑若已知长度为,如何快速求出子数组最大值,可以用前缀和来O(1)的去解决,然后遍历所有的子数组左端点,时间复杂度总共
。接下来考虑所有质数情况:

范围内的质数共有9592个,考虑遍历所有情况:总共的复杂度为
约为
,直接暴力做还是能过的,所以直接暴力冲就行。
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
vector<LL>prime;//存储素数
bool vis[N+5];
void su()
{for(int i=2;i<=N;i++){if(!vis[i])prime.pb(i);for(int j=0;j < prime.size() && prime[j] * i <= N;j ++){vis[prime[j]*i]=1;if(i % prime[j]==0)break;}}
}
void solve()
{cin >> n;int sum[n + 5];sum[0] = 0;for(int i = 1 ; i <= n ; i ++)cin >> a[i] , sum[i] = sum[i - 1] + a[i];int maxx = -1e9;for(int i = 0 ; i < prime.size() ; i ++){int len = prime[i];if(len > n){break;}for(int j = len ; j <= n ; j ++){maxx = max(maxx , sum[j] - sum[j - len]);}}cout << maxx;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;su();//cin>>t;while(t--){solve();}return 0;
}
4. 合并石子加强版

思路:若只关注一个石头:发现最终他的贡献为其自身权值与其他所有石头权值乘积之和。而其他所有石头也是一样的。因此最终的代价和合并石子的顺序无关,只需要按顺序模拟即可。(longlong会爆,需要unsigned long long )
#include <iostream>
using namespace std;
#define int unsigned long long
signed main()
{int n;cin >> n;int a[n];for(int i = 0 ; i < n ; i ++)cin >> a[i];int sum = a[0];int tot = 0;for(int i = 1 ; i < n ; i ++){tot += a[i] * sum;sum += a[i];}cout << tot;return 0;
}5. 简单的LIS问题

思路:可以发现:修改一个数之后的效果最多能够使得LIS增加1。接下来考虑怎么添加能保证上升子序列增加1:
1、若当前上升子序列不包含最后一个元素,那么将最后一个元素设为就一定能使得上升子序列加一。
2、若上升子序列的开头不为0且不为第一个数,那么将第一个数改为就一定能使得上升子序列增加1。
3、修改子序列中相邻两个数之间的某个数,使得
。
所以我们需要知道的是:以某个数开头往后所能形成的最长上升子序列以及以某个数结尾能够形成的最长上升子序列。分别设为以及
,对应了以
结尾能够形成最长上升子序列长度以及以
开头能够形成的最长上升子序列长度。
对于情况1和情况2,可以直接通过函数来求解,对于情况3,可以想到将
与
合并,即最长上升子序列长度为
,当
时,则能够在
之间修改一个数使得LIS增加1。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,ans;
int a[5001],l[5001],r[5001];
signed main()
{cin >> n;for(int i = 1 ; i <= n ; i ++)cin >> a[i];for(int i = 1 ; i <= n ; i ++){l[i] = r[i] = 1;}for(int i = 2 ; i <= n ; i ++){for(int j = 1 ; j < i ; j ++){if(a[i] > a[j])l[i] = max(l[i] , l[j] + 1);}}for(int i = n ; i >= 1 ; i --){for(int j = n ; j > i ; j --){if(a[i] < a[j])r[i] = max(r[i] , r[j] + 1);}}for (int i = 1;i <= n ; i ++){if(i < n){//等效于将末尾设为10^1000ans = max(ans , l[i] + 1);}else{ans = max(ans , l[i]);}if(i != 1 && a[i] != 0){//等效于将 a1 设为0ans = max(ans , r[i] + 1);}else{ans = max(ans , r[i]);}for(int j = i + 2 ; j <= n ; j ++)//等效于将i ~ j 当中的一个数设为ai + 1if (a[j] - a[i] > 1)ans = max(ans , l[i] + r[j] + 1);}cout << ans;
}6. 期望次数

思路:一道期望DP的板子题,定义为当前
时,需要达到目标M的操作期望。
定义为权值总和,定义
为将
的权值。
接下来考虑转移方程:
化简之后得到:
之后就从后往前DP即可,最终输出.
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 998244353;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
LL qpow(LL a , LL b)//快速幂
{LL sum=1;while(b){if(b&1){sum=sum*a%mod;}a=a*a%mod;b>>=1;}return sum;
}
int dp[N];//从i到最终状态的期望次数
//sum - a[1] / sum dp[i] = Σ(dp[i * j] * a[i * j] / sum) + 1
// dp[i] = Σdp[i * j] * a[i * j] + sum / sum - a[i]
void solve()
{cin >> n >> m;int sum = 0;for(int i = 1 ; i <= n ; i ++){cin >> a[i];sum += a[i];}for(int i = m - 1 ; i >= 1 ; i --){for(int j = 2 ; j <= n && j * i < m ; j ++){dp[i] += a[j] * dp[i * j];dp[i] %= mod;}dp[i] += sum;dp[i] %= mod;dp[i] *= qpow(sum - a[1] , mod - 2);dp[i] %= mod;}cout << dp[1];
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}
相关文章:
蓝桥杯小白赛第一场(1~6)(期望DP)
1、模拟 2、贪心 3、前缀和 4、猜结论 5、双指针 6、期望DP(公式有问题已更改) 1. 蘑菇炸弹 思路:一个简单的暴力模拟。 #include <bits/stdc.h> using namespace std; int main() {int n;cin >> n;vector<int>a(n…...

房贷背后数学陷阱-蒙特卡洛算法Monte Carlo揭秘断供为何越来越多(硬核收藏)
前几天写了法拍房相关文章,发现国内断供的房屋越来越多。 中国法拍房数量统计预测模型_2023年法拍房数据竟是 2023年中国法拍房用户画像和数据分析 今早花了2个小时,写了蒙特卡洛算法模拟预测按揭贷款断供概率。 先给大家介绍按揭贷款的常用数据。不同…...
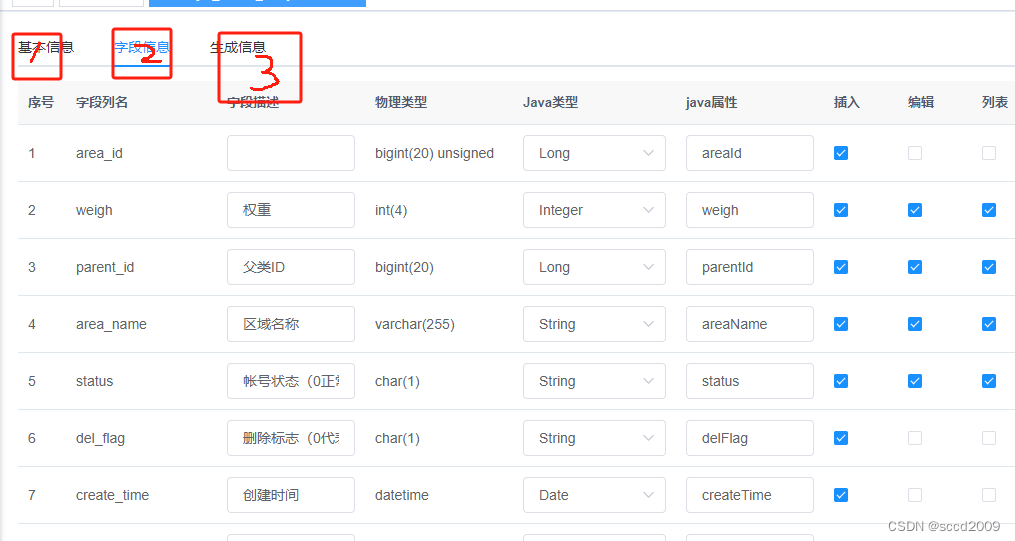
spingboot项目实战之若依框架创建新模块
前言 目前的脚手架系统很多,比较早接触诺依框架,以若依框架为参考如何创建新模块 步骤 1. 下载诺依框架,依照参考说明一步步,能做到系统运行起来。 2. 准备好mysql文件,创建新数据库表 3. 数据库管理工具navicat…...

智能优化算法应用:基于飞蛾扑火算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于飞蛾扑火算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于飞蛾扑火算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.飞蛾扑火算法4.实验参数设定5.算法结果6.…...

3分钟,掌握“曲面屏显示屏”
在3分钟内掌握“曲面屏显示屏”的概念和特点,可以按照以下步骤进行: 一、了解曲面屏显示屏的基本概念 曲面屏显示屏是一种采用柔性塑料的显示屏,主要通过OLED面板来实现。相比直面屏幕,曲面屏幕弹性更好,不易破碎。此外…...
光栅化渲染:光栅化算法实现
光栅化是将图元转换为二维图像的过程。 该图像的每个点都包含颜色和深度等信息。 因此,对图元进行光栅化由两部分组成。 第一个是确定窗口坐标中整数网格的哪些方格被图元占据。 第二个是为每个这样的方块分配颜色和深度值。 (OpenGL 规范) N…...

Python-Opencv图像处理的小坑
1.背景 最近在做一点图像处理的事情,在做处理时的cv2遇到一些小坑,希望大家遇到的相关的问题可以注意!! 2. cv2.imwrite保存图像 cv2.imwrite(filename, img, [params]) filename:需要写入的文件名,包括路…...

[LCTF 2018]bestphp‘s revenge
文章目录 前置知识call_user_func()函数session反序列化PHP原生类SoapClient 解题步骤 前置知识 call_user_func()函数 把第一个参数作为回调函数调用 eg:通过函数的方式回调 <?php function barber($type){echo "you wanted a $type haircut, no problem\n";}c…...

HTML中常用表单元素使用(详解!)
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍HTML中常用表单元素使用以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获,友友们有任何问题可以在评论区留言 …...

掌握C++模板的艺术:类型参数、默认值和自动推导
掌握C模板的艺术:类型参数、默认值和自动推导 模板参数 类型模板参数 在 Grid 示例中,Grid 模板有一个模板参数:存储在网格中的类型。编写类模板时,您需要在尖括号内指定参数列表,例如: template <typename T&g…...
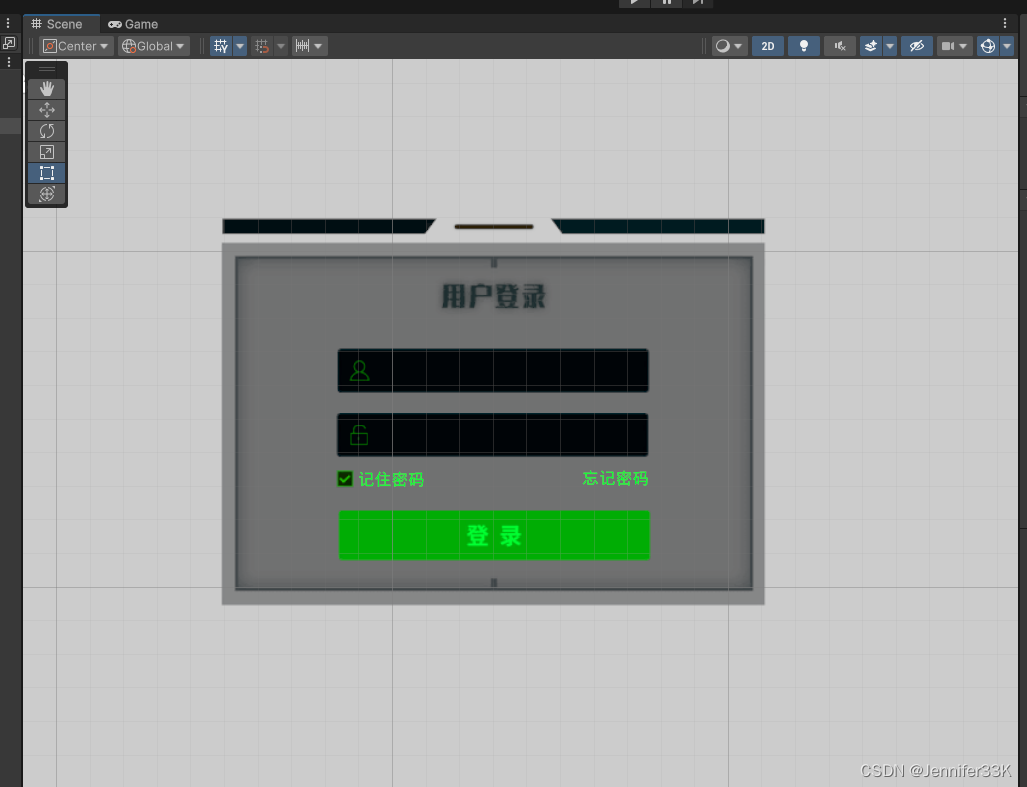
Unity_使用FairyGUI搭建登录页面
Unity_使用FairyGUI搭建登录页面 1. 使用FairyGUI准备一个UI界面,例如:以下登录 2. 发布导出(发布路径设置为Unity的Asset下任何路径) 3. Unity编辑器安装FairyGUI包资源(在资源商店找见并存储为我的资源,…...

百岁时代即将来临,原知因成为消费新潮流
什么叫长寿时代?泰康保险首席执行官陈东升指出:长寿时代,就是百岁人生即将来临,人人带病长期生存。而在这个时代,人类最大的变化在于“生命尺度的改变”,比如过去20岁是年轻人,40岁中年人,60岁…...
16:00的面试,16:07就出来了,问的问题过于变态了。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到六月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40…...

VUE宝典之el-dialog使用
文章目录 🍁前言🍁el-dialog简介🍁el-dialog属性🍁el-dialog示例🍁父子组件值传递示例 🍁前言 el-dialog是Element UI库中的一个重要组件,用于在Vue应用程序中创建弹出框。它提供了一组实用的属…...

Cocos Creator:坐标系
Cocos Creator:坐标系 坐标系节点位置坐标转换v3.8 实现原理(不想了解可以直接跳过)简单示例:(干货or解决方案在这里!) 锚点缩放和旋转 总结心得 在 Cocos Creator 3.8 中,节点坐标系…...
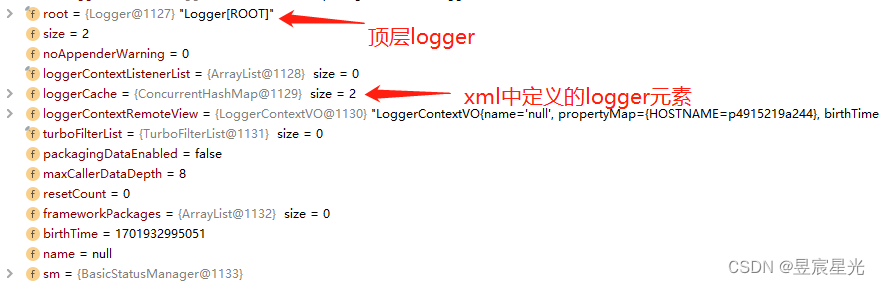
logback日志框架使用
依赖引入 <dependency><groupId>ch.qos.logback</groupId><artifactId>logback-classic</artifactId><version>1.1.7</version> </dependency> 使用logback日志框架只需要引入以上即可,(我们平时使用较多的Slf4j…...
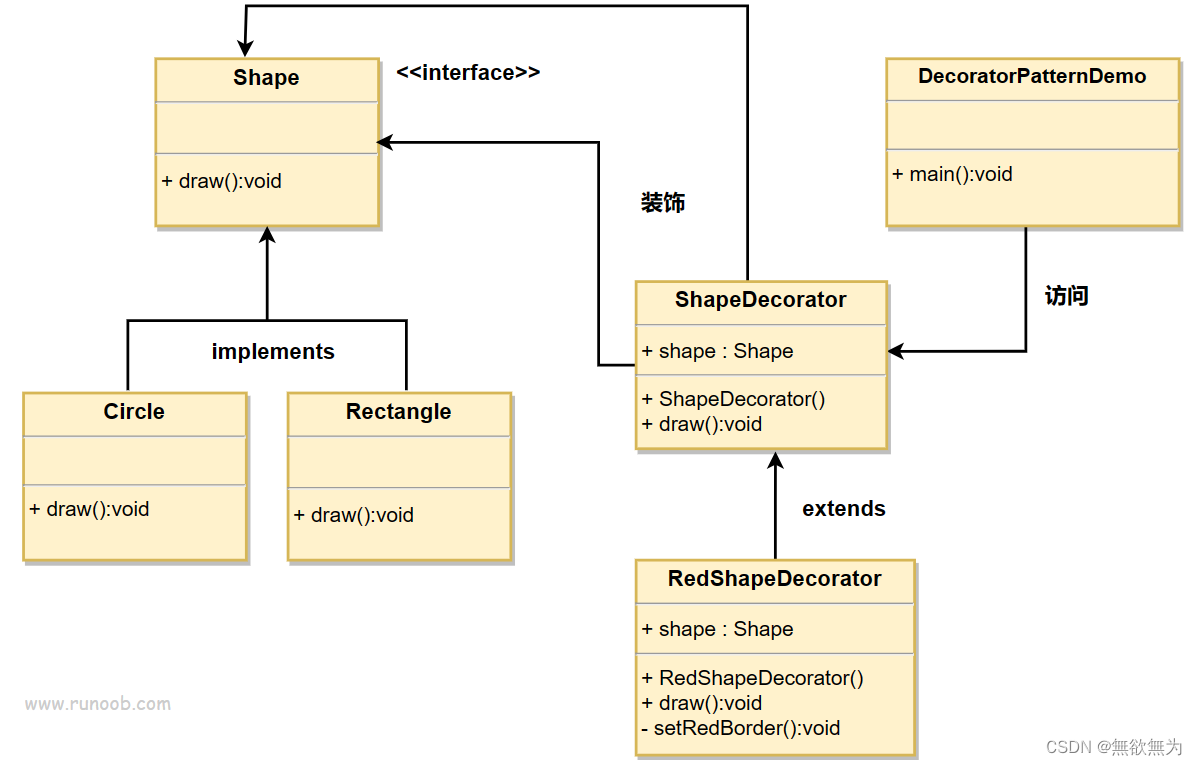
【八】python装饰器模式
文章目录 8.1 装饰器模式简介8.2 装饰器模式作用8.3 装饰器模式构成8.3.1 装饰器模式包含以下几个核心角色:8.3.2 UML类图 8.4 装饰器模式python代码实现8.4.1 基本装饰器的使用8.4.2 多个装饰器的执行顺序8.4.3 带返回值的装饰器的使用8.4.4 装饰器模式-关联类模式…...

Unity-小工具-LookAt
Unity-小工具-LookAt 🥙介绍 🥙介绍 💡通过扩展方法调用 gameObject.LookAtTarget,让物体转向目标位置 💡gameObject.StopLookat 停止更新 💡可以在调用时传入自动停止标记,等转向目标位置后自…...

TCP实现一对一聊天
一,创建类 二,类 1.ChatSocketServer类 import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Socket; import java.util.Sca…...
全面高压化与全面超快充,破解新能源汽车的时代难题
是什么让新能源车主感到疲惫与焦虑?是什么阻挡更多消费者选择新能源汽车?我们在身边进行一个简单的调查就会发现,问题的答案非常一致:充电。 充电难,充电慢的难题,始终是困扰新能源汽车产业发展,…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
