透析回溯的模板
| 关卡名 | 认识回溯思想 | 我会了✔️ |
| 内容 | 1.复习递归和N叉树,理解相关代码是如何实现的 | ✔️ |
| 2.理解回溯到底怎么回事 | ✔️ | |
| 3.掌握如何使用回溯来解决二叉树的路径问题 | ✔️ |
回溯可以视为递归的拓展,很多思想和解法都与递归密切相关,在很多材料中都将回溯都与递归同时解释,例如本章2.1的路径问题就可以使用递归和回溯两种方法来解决。因此学习回溯时,我们对比递归来分析其特征会理解更深刻。
关于递归和回溯的区别,我们设想一个场景,某猛男想脱单,现在有两种策略:
- 1.递归策略:先与意中人制造偶遇,然后了解人家的情况,然后约人家吃饭,有好感之后尝试拉人家的手,没有拒绝就表白。
- 2.回溯策略:先统计周围所有的单身女孩,然后一个一个表白, 被拒绝就说“我喝醉了”,然后就当啥也没发生,继续找下一个。
其实回溯本质就这么个过程,请读者学习本章时认真揣摩这个过程。
回溯最大的好处是有非常明确的模板,所有的回溯都是一个大框架,因此透彻理解回溯的框架是解决一切回溯问题的基础。第一章我们只干一件事,那就是分析这个框架。
回溯不是万能的,而且能解决的问题也是非常明确的,例如组合、分割、子集、排列,棋盘等等,不过这些问题具体处理时又有很多不同,本章我们梳理了多个最为热门的问题来解释,请同学们认真对待。
回溯可以理解为递归的拓展,而代码结构又特别像深度遍历N叉树,因此只要知道递归,理解回溯并不难,难在很多人不理解为什么在递归语句之后要有个“撤销”的操作。 我们会通过图示轻松给你解释该问题。这里先假设一个场景,你谈了个新女朋友,来你家之前,你是否会将你前任的东西赶紧藏起来?回溯也一样,有些信息是前任的,要先处理掉才能重新开始。
回溯最让人激动的是有非常清晰的解题模板,如下所示,大部分的回溯代码框架都是这个样子,具体为什么这样子我们后面再解释。
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择本层集合中元素(画成树,就是树节点孩子的大小)){处理节点;backtracking();回溯,撤销处理结果;}}回溯是有明确的解题模板的,本章我们只干一件事——分析回溯的模板。
1 从N叉树说起
在解释回溯之前, 我们先看一下N叉树遍历的问题,我们知道在二叉树中,按照前序遍历的过程如下所示:
void treeDFS(TreeNode root) {if (root == null)return;System.out.println(root.val);treeDFS(root.left);treeDFS(root.right);
}class TreeNode{int val;TreeNode left;TreeNode right;
}假如我现在是一个三叉、四叉甚至N叉树该怎么办呢?很显然这时候就不能用left和right来表示分支了,使用一个List比较好,也就是这样子:
class TreeNode{int val;List<TreeNode> nodes;
}遍历的代码:
public static void treeDFS(TreeNode root) {//递归必须要有终止条件if (root == null){return;}// 处理节点System.out.println(root.val);//通过循环,分别遍历N个子树for (int i = 1; i <= nodes.length; i++) {treeDFS("第i个子节点");}
}到这里,你有没有发现和上面说的回溯的模板非常像了?是的!非常像!既然很像,那说明两者一定存在某种关系。其他暂时不管,现在你只要先明白回溯的大框架就是遍历N叉树就行了。
2 为什么有的问题暴力搜索也不行
我们说回溯主要解决暴力枚举也解决不了的问题,什么问题这么神奇,暴力都搞不定?
看个例子:
LeetCode77 :给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。例如,输入n=4,k=2,则输出:
[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]
首先明确这个题是什么意思,如果n=4,k=2,那就是从4个数中选择2个,问你最后能选出多少组数据。
这个是高中数学中的一个内容,过程大致这样:如果n=4,那就是所有的数字为{1,2,3,4}
- 1.先取一个1,则有[1,2],[1,3],[1,4]三种可能。
- 2.然后取一个2,因为1已经取过了,不再取,则有[2,3],[2,4]两种可能。
- 3.再取一个3,因为1和2都取过了,不再取,则有[3,4]一种可能。
- 4.再取4,因为1,2,3都已经取过了,所以直接返回null。
- 5.所以最终结果就是[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]。
这就是我们思考该问题的基本过程,写成代码也很容易,双层循环轻松搞定:
int n = 4;for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {System.out.println(i + " " + j);}}假如n和k都变大,比如n是200,k是3呢?也可以,三层循环基本搞定:
int n = 200;for (int i = 1; i <= n; i++) {for (int j = i + 1; j <= n; j++) {for (int u = j + 1; u <= n; n++) {System.out.println(i + " " + j + " " + u);}} 如何这里的K是5呢?甚至是50呢?你需要套多少层循环?甚至告诉你K就是一个未知的正整数k,你怎么写循环呢?这时候已经无能为例了?所以暴力搜索就不行了。
这就是组合类型问题,除此之外子集、排列、切割、棋盘等方面都有类似的问题,因此我们要找更好的方式。
3 回溯=递归+局部枚举+放下前任
我们继续研究LeetCode77题,我们图示一下上面自己枚举所有答案的过程。
n=4时,我们可以选择的n有 {1,2,3,4}这四种情况,所以我们从第一层到第二层的分支有四个,分别表示可以取1,2,3,4。而且这里 从左向右取数,取过的数,不在重复取。 第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。
横向:
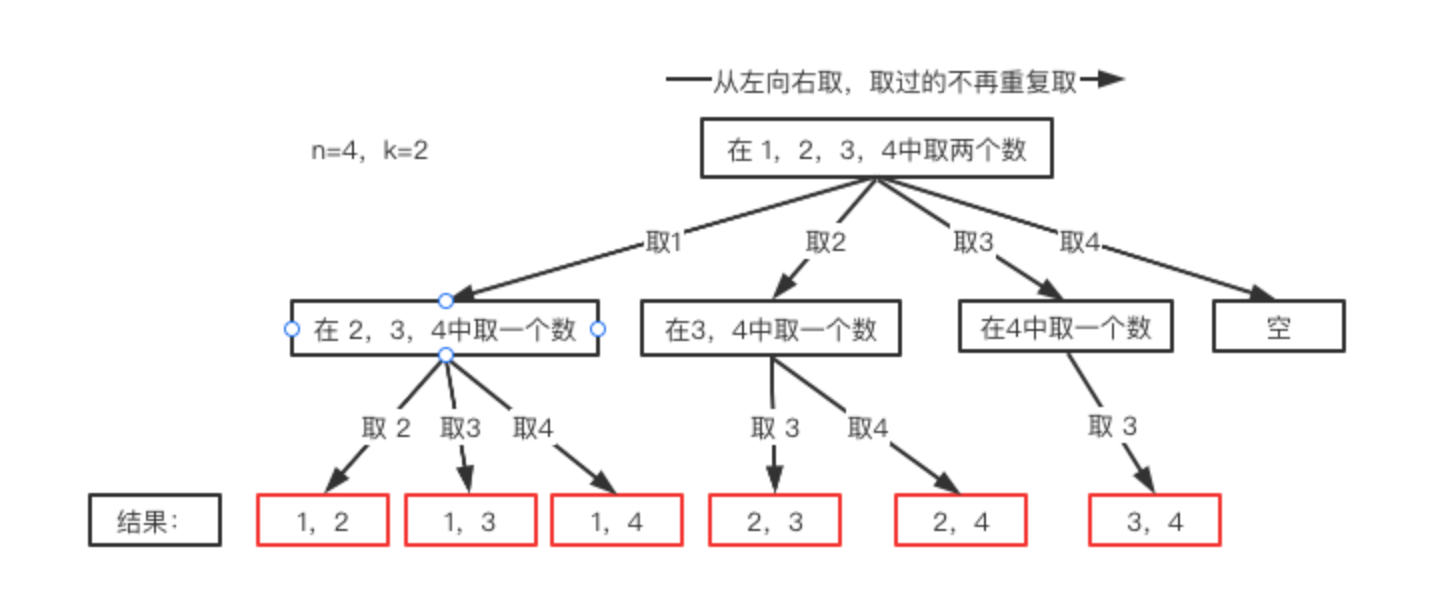
每次从集合中选取元素,可选择的范围会逐步收缩,到了取4时就直接为空了。
继续观察树结构,可以发现,图中每次访问到一次叶子节点(图中红框标记处),我们就找到了一个结果。虽然最后一个是空,但是不影响结果。这相当于只需要把从根节点开始每次选择的内容(分支)达到叶子节点时,将其收集起来就是想要的结果。
如果感觉不明显,我们再画一个n=5,k=3的例子:
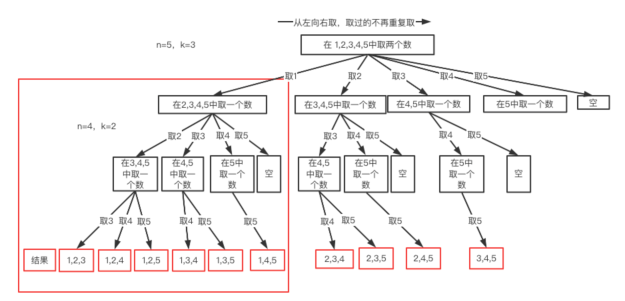
从图中我们发现元素个数n相当于树的宽度(横向),而每个结果的元素个数k相当于树的深度(纵向)。所以我们说回溯算法就是一纵一横而已。再分析,我们还发现几个规律:
① 我们每次选择都是从类似{1,2,3,4},{1,2,3,4,5}这样的序列中一个个选的,这就是局部枚举,而且越往后枚举范围越小。
② 枚举时,我们就是简单的暴力测试而已,一个个验证,能否满足要求,从上图可以看到,这就是N叉树遍历的过程,因此两者代码也必然很像。
③ 我们再看上图中红色大框起来的部分,这个部分的执行过程与n=4,k=2的处理过程完全一致,很明显这是个可以递归的子结构。
这样我们就将回溯与N叉树的完美结合在一起了。
到此,还有一个大问题没有解决,回溯一般会有个手动撤销的操作,为什么要这样呢?继续观察纵横图:
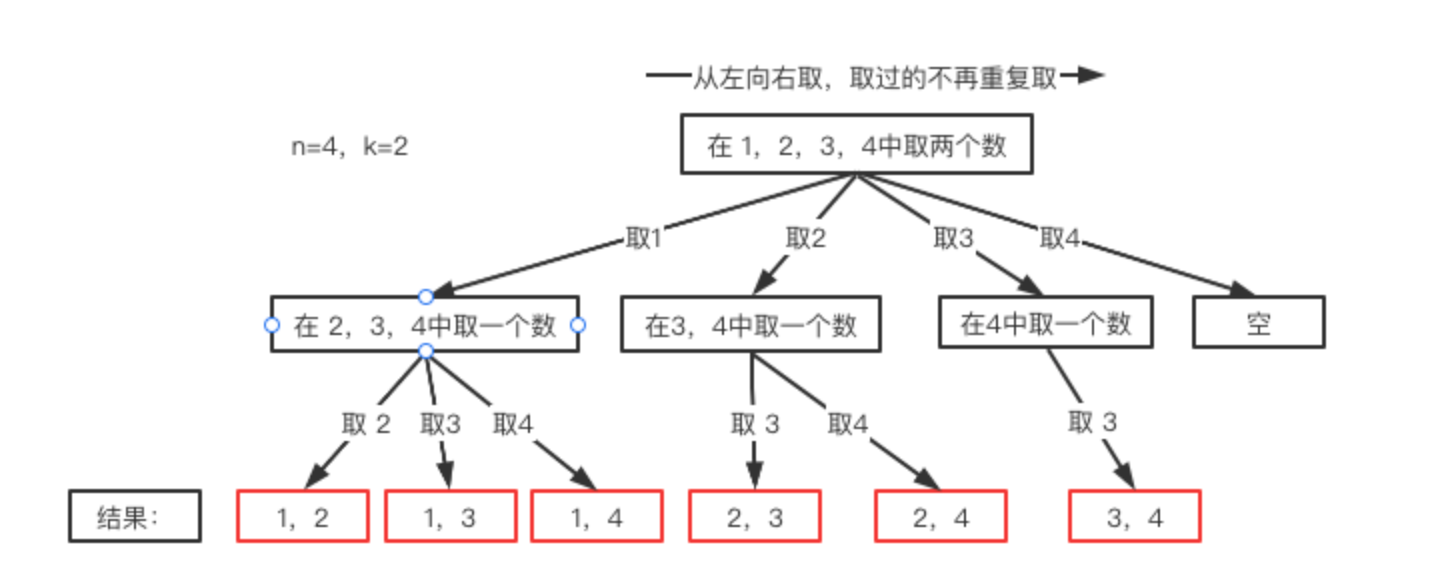
我们可以看到,我们收集每个结果不是针对叶子结点的,而是针对树枝的,比如最上层我们首先选了1,下层如果选2,结果就是{1,2},如果下层选了3,结果就是{1,3},依次类推。现在的问题是当我们得到第一个结果{1,2}之后,怎么得到第二个结果{1,3}呢?
继续观察纵横图,可以看到,我可以在得到{1,2}之后将2撤掉,再继续取3,这样就得到了{1,3},同理可以得到{1,4},之后当前层就没有了,我们可以将1撤销,继续从最上层取2继续进行。
这里对应的代码操作就是先将第一个结果放在临时列表path里,得到第一个结果{1,2}之后就将path里的内容放进结果列表resultList中,之后,将path里的2撤销掉, 继续寻找下一个结果{1.3},然后继续将path放入resultLit,然后再撤销继续找。
现在明白为什么要手动撤销了吧,这个过程,我称之为"放下前任,继续前进",后面所有的回溯问题都是这样的思路。
这几条就是回溯的基本规律,明白之后,一切都变得豁然开朗。如果还是不太明白,我们下一小节用更完整的图示解释该过程。
到此我们就可以写出完整的回溯代码了:
public List<List<Integer>> combine(int n, int k) {List<List<Integer>> resultList = new ArrayList<>();if(k<=0 || n<k){return resultList;}// 用户返回结果Deque<Integer> path = new ArrayList<>();dfs(n,k,1,path,resultList);return resultList;
}
public void dfs(int n,int k,int startIndex,Deque path,List<List<Integer>> resultList){// 递归终止条件是:path 的长度等于 kif(path.size()==k){resultList.add(new ArrayList<>(path));return;}// 针对一个结点,遍历可能的搜索起点,其实就是枚举for(int i=startIndex;i<=n;i++){// 向路径变量里添加一个数,就是上图中的一个树枝的值path.addLast(i);// 搜索起点要加1是为了缩小范围,下一轮递归做准备,因为不允许出现重复的元素dfs(n,k,i+1,path,resultList);// 递归之后需要做相同操作的逆向操作,具体后面继续解释path.removeLast();}
} 上面代码还有个问题要解释一下:startIndex和i是怎么变化的,为什么传给下一层时要加1。
我们可以看到在递归里有个循环
for (int i = startIndex; i <= n; i++) {dfs(n,k,i+1,path,res);}这里的循环有什么作用呢?看一下图就知道了,这里其实就是枚举,第一次n=4,可以选择1 ,2,3,4四种情况,所以就有四个分支,for循环就会执行四次:
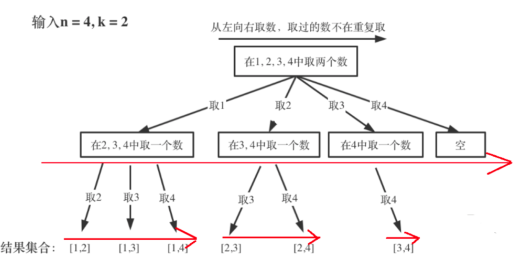
而对于第二层第一个,选择了1之后,剩下的元素只有2 ,3, 4了,所以这时候for循环就执行3次,后面的则只有2次和1次。
4 图解为什么有个撤销的操作
如果你已经明白上面为什么会有撤销过程,这一小节就不必看了。如果还是不懂,本节就用更详细的图示带你看一下。 回溯最难理解的部分是这个回溯过程,而且这个过程即使调试也经常会晕:
path.addLast(i);
dfs(n, k, i + 1, path, res);
path.removeLast();
为什么要remove呢?看下图,当第一层取1时,最底层的边从左向右依次执行“取2”、“取3”和“取4”,而取3的时候,此时list里面存的是上一个结果<1,2>,所以必须提前将2撤销,这就path.removeLast();的作用。
用我们拆解递归的方法,将递归拆分成函数调用,输出第一条路径{1,2}的步骤如下如下:
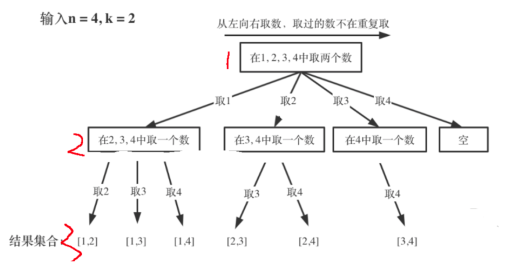
我们在递归章节说过,递归是“不撞南墙不回头”,回溯也一样,接下来画代码的执行图详细看一下其过程,图中的手绘的序号是执行过程:
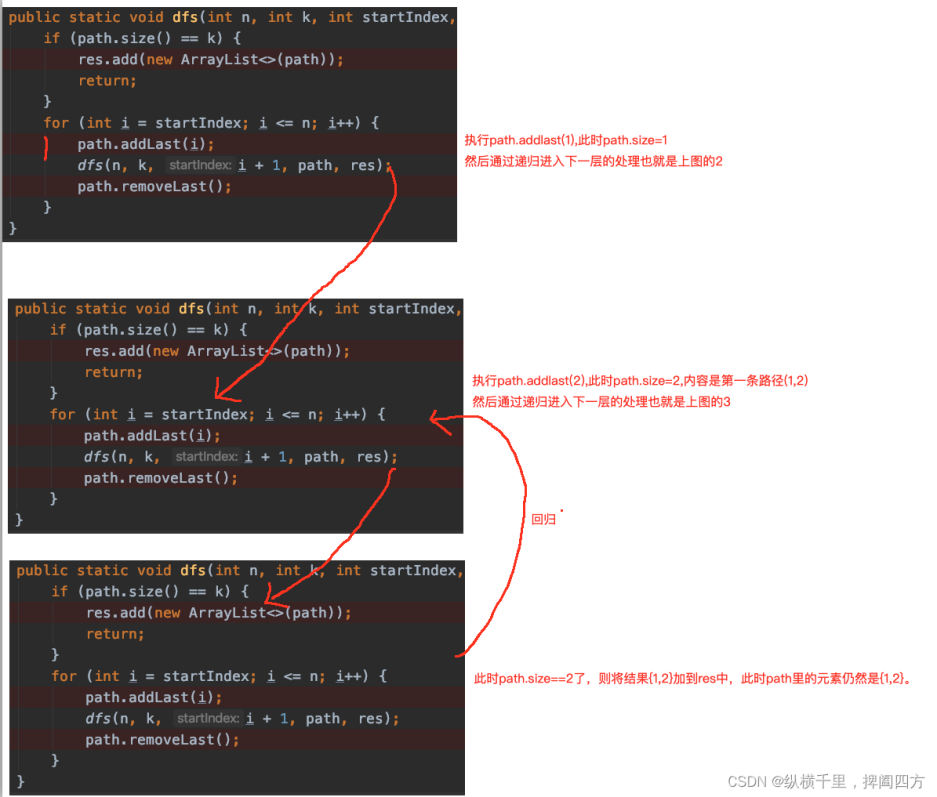
然后呢?{1,2}输出 之后会怎么执行呢?回归之后,假如我们将remove代码去掉,也就是这样子:
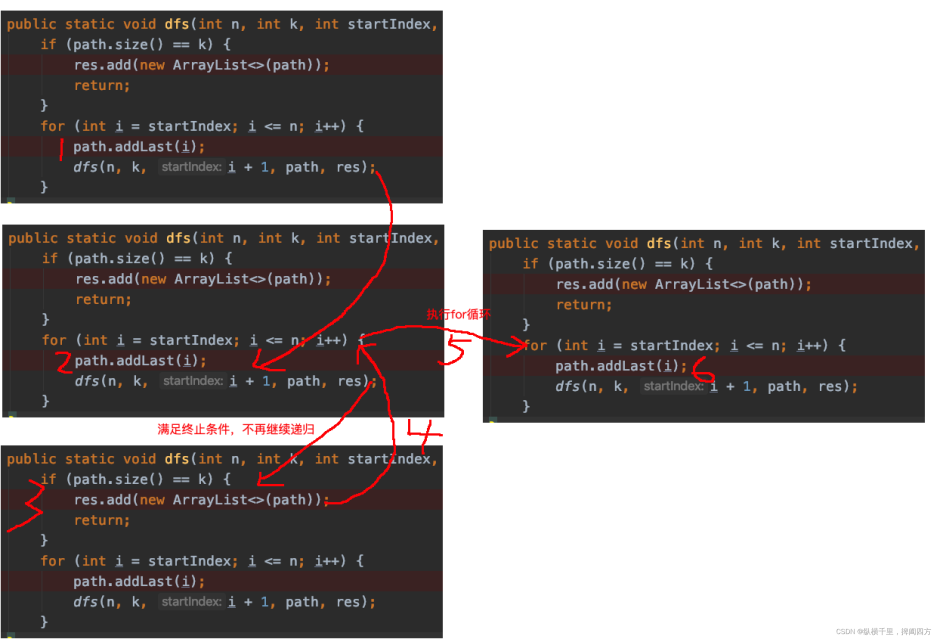
注意上面的4号位置结束之后,当前递归就结束了,然后返回到上一层继续执行for循环体,也就是上面的5。进入5之后,接着开始执行第6步:path.addLast(i)了,此时path的大小是3,元素是{1,2,3},为什么会这样呢?
因为path是一个全局的引用,各个递归函数共用的,所以当{1,2}处理完之后,2污染了path变量。我们希望将1保留而将2干掉,然后让3进来,这样才能得到{1,3},所以这时候需要手动remove一下。
同样3处理完之后,我们也不希望3污染接下来的{1,4},1全部走完之后也不希望1污染接下来的{2,3}等等,这就是为什么回溯里会在递归之后有一个remove撤销操作。
5 回溯热身—再论二叉树的路径问题
5.1 输出二叉树的所有路径
LeetCode257:给你一个二叉树的根节点root ,按任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点是指没有子节点的节点。
示例:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
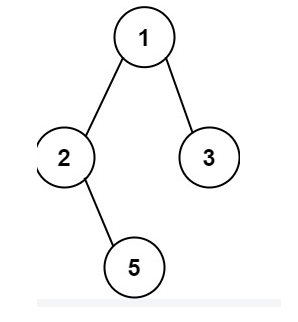
我们可以注意到有几个叶子节点,就有几条路径,那如何找叶子节点呢?我们知道深度优先搜索就是从根节点开始一直找到叶子结点,我们这里可以先判断当前节点是不是叶子结点,再决定是不是向下走,如果是叶子结点,我们就增加一条路径。
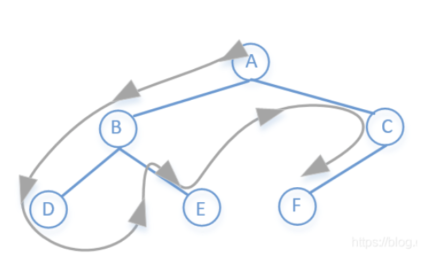
我们现在从回溯的角度来分析,得到第一条路径ABD之后怎么找到第二条路径ABE,这里很明显就是先将D撤销,然后再继续递归就可以了
class BinaryTreePaths {List<String> ans = new ArrayList<>();public List<String> binaryTreePaths(TreeNode root) {dfs(root,new ArrayList<>());return ans;}private void dfs(TreeNode root, List<Integer> temp){if(root==null){return;}temp.add(root.val);//如果是叶子节点记录结果if(root.left==null&&root.right==null){ans.add(getPathString(temp));}dfs(root.left,temp);dfs(root.right,temp);temp.remove(temp.size()-1);}//拼接结果private String getPathString(List<Integer> temp){StringBuilder sb = new StringBuilder();sb.append(temp.get(0));for(int i=1;i<temp.length();i++){sb.append("->").append(temp.get(i));}return sb.toString();}
}5.2 路径总和问题
同样的问题是LeetCode113题,给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
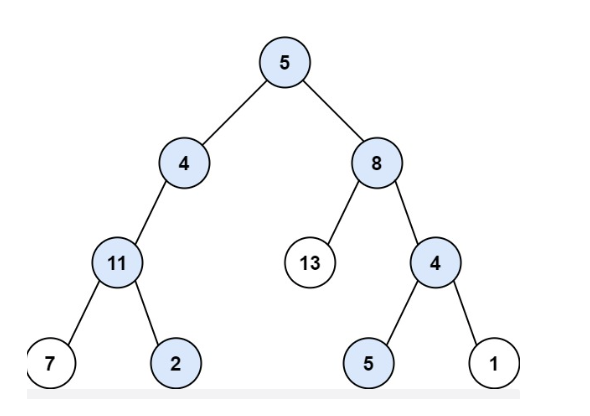
本题怎么做呢?我们直接观察题目给的示意图即可,要找的targetSum是22。我们发现根节点是5,因此只要从左侧或者右侧找到targetSum是17的即可。继续看左子树,我们发现值为4,那只要从node(4)的左右子树中找targetSum是13即可,依次类推,当我们到达node(11)时,我们需要再找和为2的子链路,显然此时node(7)已经超了,不是我们要的,此时就要将node(7)给移除掉,继续访问node(2).
同样在根结点的右侧,我们也要找总和为17的链路,方式与上面的一致。完整代码就是:
class PathSum {List<List<Integer>> res=new ArrayList<>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {LinkedList<Integer> path=new LinkedList<>();dfs(root,targetSum,path);return res;}public void dfs(TreeNode root,int targetSum,LinkedList<Integer> path){if(root==null){return;}//这个值有很关键的作用targetSum-=root.val;path.add(root.val);if(targetSum==0 && root.left==null && root.right==null){res.add(new LinkedList(path));}dfs(root.left,targetSum,path);dfs(root.right,targetSum,path);path.removeLast();}
}相关文章:

透析回溯的模板
关卡名 认识回溯思想 我会了✔️ 内容 1.复习递归和N叉树,理解相关代码是如何实现的 ✔️ 2.理解回溯到底怎么回事 ✔️ 3.掌握如何使用回溯来解决二叉树的路径问题 ✔️ 回溯可以视为递归的拓展,很多思想和解法都与递归密切相关,在很多…...

浅谈web性能测试
什么是性能测试? web性能应该注意些什么? 性能测试,简而言之就是模仿用户对一个系统进行大批量的操作,得出系统各项性能指标和性能瓶颈,并从中发现存在的问题,通过多方协助调优的过程。而web端的性能测试…...
Qt 容器QGroupBox带有标题的组框框架
控件简介 QGroupBox 小部件提供一个带有标题的组框框架。一般与一组或者是同类型的部件一起使用。教你会用,怎么用的强大就靠你了靓仔、靓妹。 用法示例 例 qgroupbox,组框示例(难度:简单),使用 3 个 QRadioButton 单选框按钮,与QVBoxLayout(垂直布局)来展示组框的…...
Linux系统解决“Key was rejected by service”
Linux系统下加载驱动模块出现如上错误提示的原因为:此驱动未经过签名。 方法一、关闭Secure Boot 如果是物理机,需要开机进入BIOS,找到“Secure Boot”的选项,然后关闭。 如果是虚拟机,可以打开虚拟设置,…...

【C++ Primer Plus学习记录】字符函数库cctype
C从C语言继承了一个与字符相关的、非常方便的函数软件包,它可以简化诸如确定字符是否为大写字母、数字、标点符号等工作,这些函数的原型是在头文件cctype中定义的。 cctype中的字符函数 函数名称返回值isalnum()如果参数是字母或数字,该函数返…...
C# WebSocket简单使用
文章目录 前言Fleck调试工具初始化简单使用 前言 最近接到了一个需求,需要网页实现上位机的功能。那就对数据传输的实时性要求很高。那就只能用WebSocket了。这里简单说一下我的WebSocket如何搭建 Fleck C# WebSocket(Fleck) 客户端:html Winfrom Fleck Github官网…...
uni-app 一些实用的页面模板
时间倒计时 <!-- 时间倒计时 --> <template><view class"container"><view class"flex-row time-box"><view class"time-item">{{ laveTimeList[0] }}</view><text>天</text><view class&qu…...
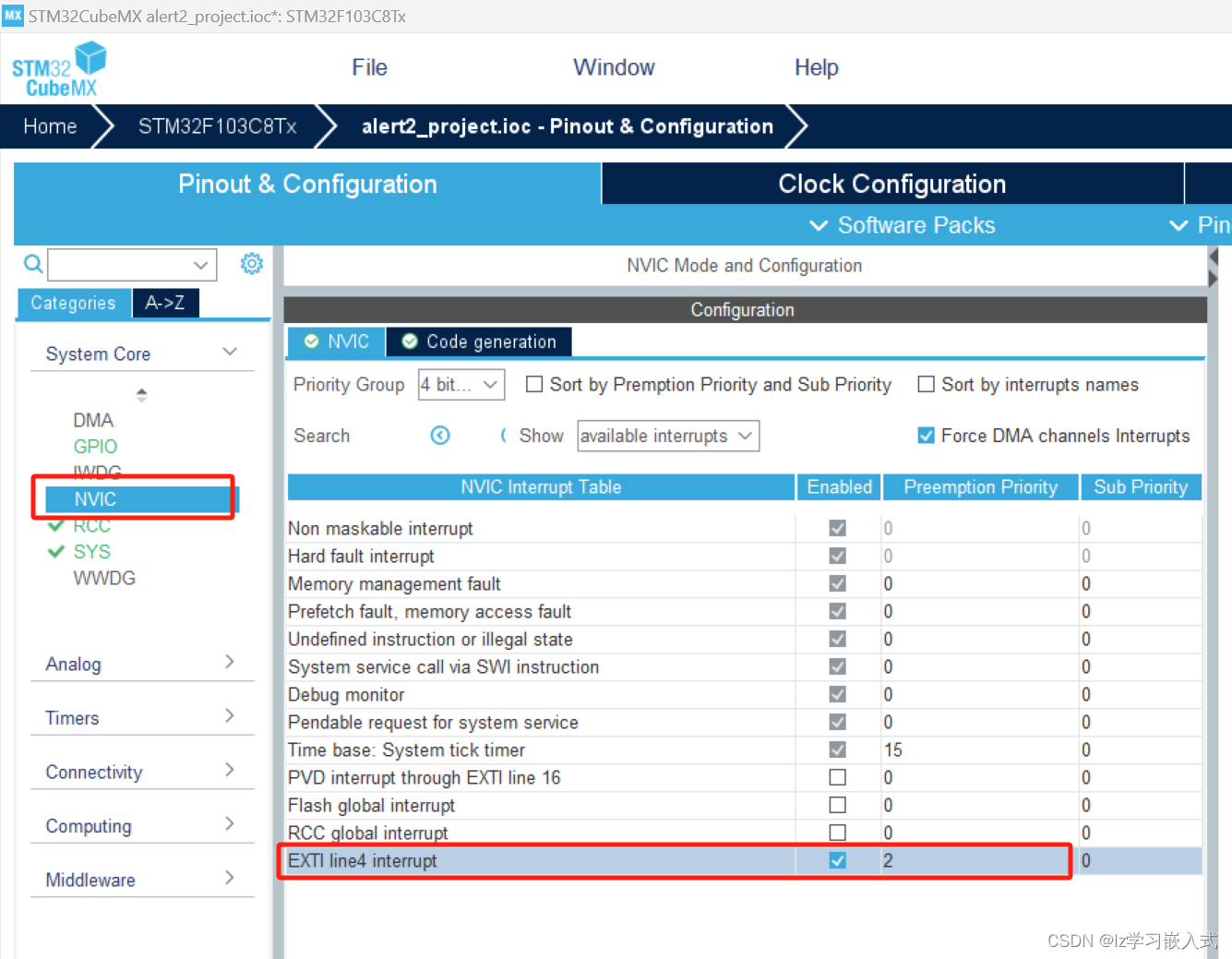
STM32——震动传感器点亮LED灯
震动传感器简单介绍 若产品不震动,模块上的 DO 口输出高电平; 若产品震动,模块上的 DO 口输出低电平,D0-LED绿色指示灯亮。 震动传感器与STM32的接线 编程实现 需求:当震动传感器接收到震动信号时,使用中断…...

使用 Timm 库替换 YOLOv8 主干网络 | 1000+ 主干融合YOLOv8
文章目录 前言版本差异说明替换方法parse_moedl( ) 方法_predict_once( ) 方法修改 yaml ,加载主干论文引用timm 是一个包含最先进计算机视觉模型、层、工具、优化器、调度器、数据加载器、数据增强和训练/评估脚本的库。 该库内置了 700 多个预训练模型,并且设计灵活易用。…...
?)
PHP中什么是闭包(Closure)?
在PHP中,闭包(Closure)是一种匿名函数,它可以作为变量传递、作为参数传递给其他函数,或者被作为函数的返回值。闭包可以在定义时捕获上下文中的变量,并在以后的执行中使用这些变量。闭包在处理回调函数、事…...

boost::graph学习
boost::graph API简单小结 boost::graph是boost为图算法提供的API,简单易用。 API说明 boost::add_vertex 创建一个顶点。 boost::add_edge 创建一条边。 boost::edges 获取所有的边。 boost::vertices 获取所有的顶点。 graph.operator[vertex_descriptor] 获…...

【C语言:动态内存管理】
文章目录 前言1.malloc2.free3.calloc4.realloc5.动态内存常见错误6.动态内存经典笔试题分析7.柔性数组8.C/C中的内存区域划分 前言 文章的标题是动态内存管理,那什么是动态内存管理?为什么有动态内存管理呢? 回顾一下以前学的知识ÿ…...

【Python基础】迭代器
文章目录 [toc]什么是迭代可迭代对象判断数据类型是否是可迭代类型 迭代器对可迭代对象进行迭代的本质获取可迭代对象的迭代器通过迭代器获取数据StopIteration异常 自定义迭代器__iter__()方法__next__()方法判断数据类型是否是可迭代类型自定义迭代器案例分离模式整合模式 fo…...
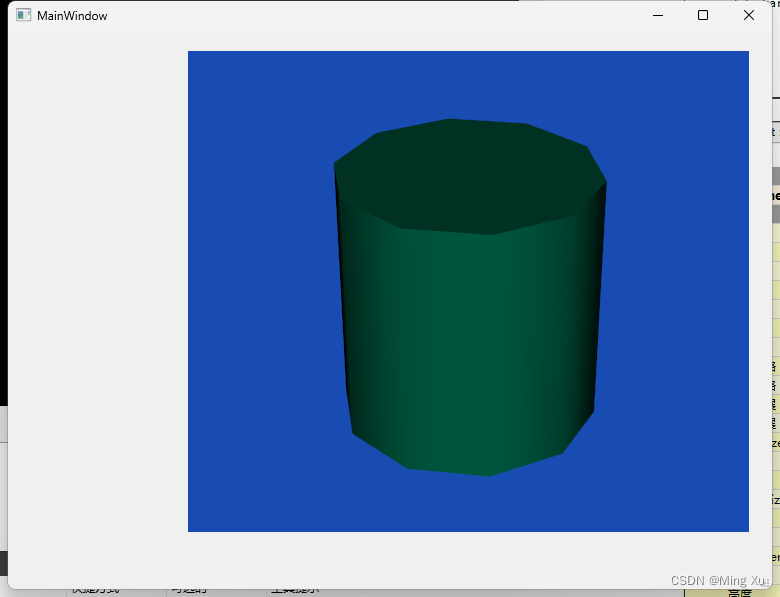
QVTK 可视化
#ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow>#include <vtkNew.h> // 智能指针 #include <QVTKOpenGLNativeWidget.h> #include <vtkCylinderSource.h> // 圆柱#include <vtkPolyDataMapper.h&g…...

【初阶C++】入门(超详解)
C入门 前言1. C关键字(C98)2. 命名空间2.1 命名空间定义2.2 命名空间使用2.3嵌套命名空间 3. C输入&输出4. 缺省参数4.1 缺省参数概念4.2 缺省参数分类 5. 函数重载5.1 函数重载概念5.2 C支持函数重载的原理--名字修饰(name Mangling) 6. 引用6.1 引用概念6.2 引用特性6.3 …...

Java正则表达式的使用
标题:Java正则表达式的使用 介绍: 正则表达式是一种强大的文本匹配模式和搜索工具。在Java中,通过使用正则表达式,我们可以快速有效地进行字符串的匹配、查找和替换。本文将介绍Java正则表达式的基本使用方法,并提供相…...
Collecting Application Engine Performance Data 收集应用程序引擎性能数据
You can collect performance data of any specific SQL action of an Application Engine program to address any performance issue. 您可以收集应用程序引擎程序的任何特定SQL操作的性能数据,以解决任何性能问题。 You can collect performance data of the S…...

C Primer Plus阅读--章节16
C Primer Plus阅读–章节16 翻译程序的第一步 预处理之前,编译器必须对该程序进行一些翻译处理。 首先,编译器将源代码中出现的字符映射到源字符集。第二,编译器定位每个反斜杠后面跟着换行符的实力,并删除他们。物理行的合并。…...
直接插入排序与希尔排序
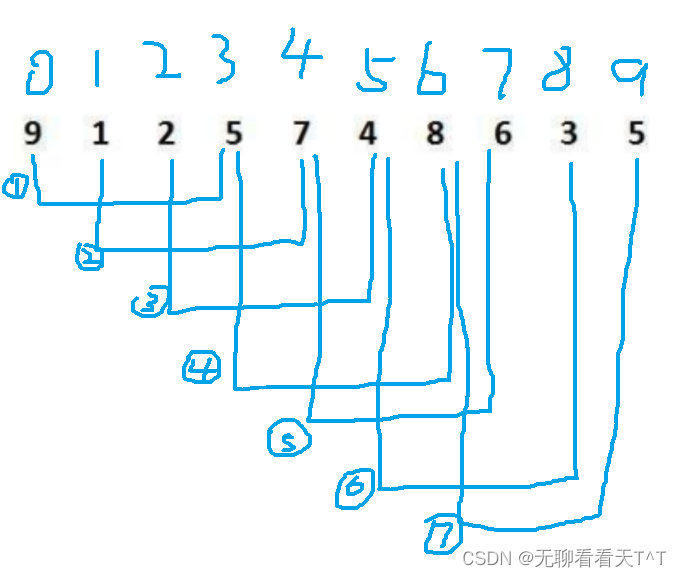
目录 前言 插入排序 直接插入排序 时空复杂度 直接插入排序的特性 希尔排序(缩小增量排序) 预排序 顺序排序 多组并排 小总结 直接插入排序 时空复杂度 希尔排序的特性 前言 字可能有点多,但是真的理解起来真的没那么难&#…...
敏捷:应对软件定义汽车时代的开发模式变革
随着软件定义汽车典型应用场景的落地,汽车从交通工具转向智能移动终端的趋势愈发明显。几十年前,一台好车的定义主要取决于高性能的底盘操稳与动力系统;几年前,一台好车的定义主要取决于智能化系统与智能交互能否满足终端用户的用…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
