C语言结构体和位段
自定义类型:结构体及联合和枚举
- 一.结构体类型的声明
- 1.1 结构体的概念
- 1.2结构的声明
- 1.3特殊的声明
- 1.4结构体的自引用
- 1.5可以使用typedef重命名
- 二.结构体变量的创建和初始化
- 2.1结构体变量的初始化使用`{}`
- 2.2初始化:定义变量的同时赋初值。
- 2.3结构体嵌套及初始化
- 三.结构体成员访问操作符
- 四.结构体内存对齐
- 4.1对齐规则
- 练习1
- 练习2
- 练习3
- 练习4(嵌套结构体的对齐数)
- 4.2修改默认对齐数
- 五.结构体传参
- 六.联合体
- 6.1联合体类型的声明
- 6.2联合体的特点
- 6.2计算联合体的大小
- 6.3用联合体判断大小端字节序
- 七.枚举类型
- 7.1枚举类型的声明
- 7.2枚举的优点
- 7.3 枚举类型的使用
一.结构体类型的声明
1.1 结构体的概念
结构是一些值的集合,这些称为成员变量,结构的每个成员可以是不同类型的变量
1.2结构的声明
struct tag
{member-list;
}variable-list;
假如是一个大学生,可以用以下带代码描述
struct Stu
{char name[20];//名字int age;//年龄char sex[5];//性别char id[20];//学号};
这里注意结构体后面的分号是不可以丢的
1.3特殊的声明
在声明结构体的时候可以使用匿名结构体
但是匿名结构体只可以使用一次
//匿名结构体类型
struct
{int a;char b;float c;
}x;
struct
{int a;char b;float c;
}a[20], *p;
编译器会把上面的两个声明当成完全不同的两个类型,所以是非法的。
匿名的结构体类型,如果没有对结构体类型重命名的话,基本上只能使⽤⼀次。
1.4结构体的自引用
在结构中包含⼀个类型为该结构本⾝的成员是可以的
比如:定义一个链表结点
struct Node
{int data;struct Node* next;
};
1.5可以使用typedef重命名
typedef struct Node
{int data;struct Node* next;
}Node;
二.结构体变量的创建和初始化
2.1结构体变量的初始化使用{}
struct Point
{int x;int y;
}s1; //声明类型的同时定义变量s1
struct Point s2; //定义结构体变量s2
2.2初始化:定义变量的同时赋初值。
struct Point p3 = {x, y};
2.3结构体嵌套及初始化
struct Node
{int data;struct Point p;struct Node* next;
}n1 = {10, {4,5}, NULL}; //结构体嵌套初始化
struct Node n2 = {20, {5, 6}, NULL};struct Stu
{char name[15];int age;
};
struct Stu s = {.age=20, .name="zhangsan"};//初始化
三.结构体成员访问操作符
结构成员访问操作符有两个⼀个是 . ,⼀个是 -> .
有以下两种方式:
结构体变量.成员变量名
结构体指针—>成员变量名
struct student
{char name[10];int age;
};int main()
{struct student stu = { "zhangsan",10 };struct student* pstu = &stu;printf("%d", (*(pstu)).age);printf("%d",pstu->age);return 0;
}
四.结构体内存对齐
4.1对齐规则
1. 结构体的第一个成员相对于结构体变量起始位置偏移量为0的地址处
2. 其他成员变量要对齐到某个数字(对齐数)的整数倍地址
3. 结构体总大小为 最大对其数(结构体中每个成员变量都有一个对齐数,所有对齐数中最大的)的整数倍
4. 如果要是嵌套了结构体的情况,嵌套的结构体成员对齐到自己成员中的最大对其数的整数倍,结构体的整体大小就是所有最大对齐数(含嵌套结构体中成员的对齐数)的整数倍
以下有几个练习:
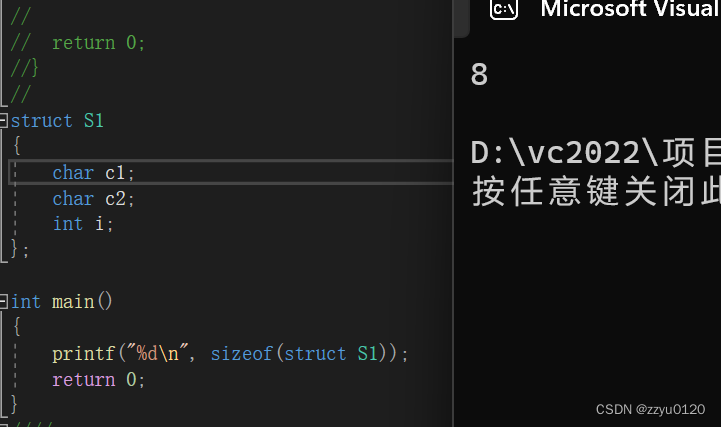
练习1
计算下列结构体大小:
struct S1
{char c1;char c2;int i;
};
printf("%d\n", sizeof(struct S1));
结果是
下面画图来解释以下原因:
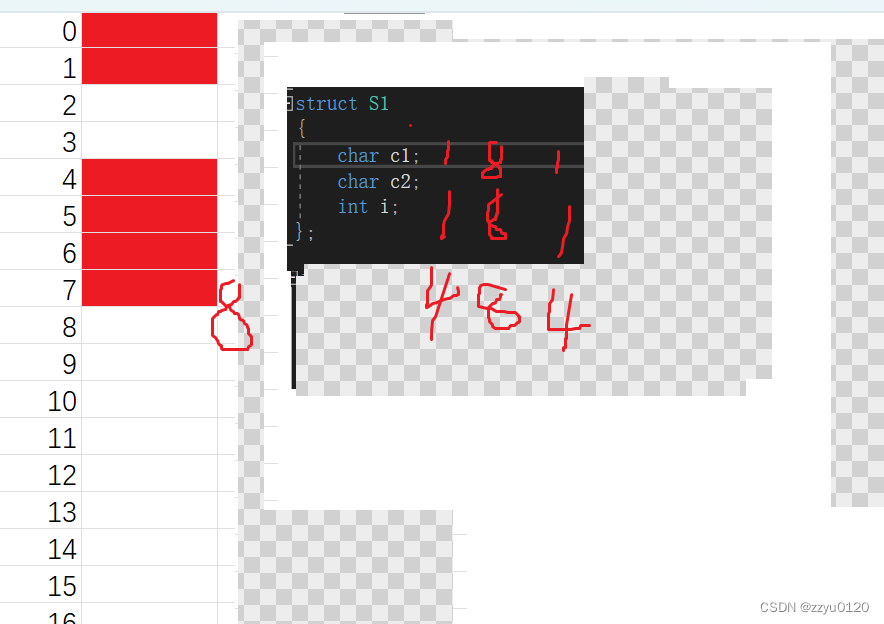
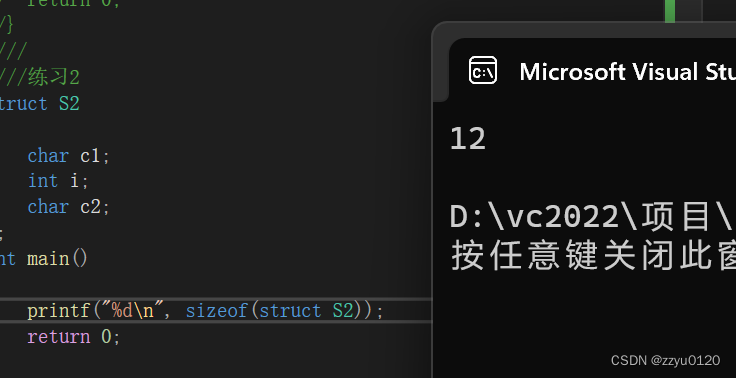
练习2
计算下列结构体大小:
struct S2
{char c1;int i;char c2;
};
int main()
{printf("%d\n", sizeof(struct S2));return 0;
}
结果是
下面画图来解释以下原因:
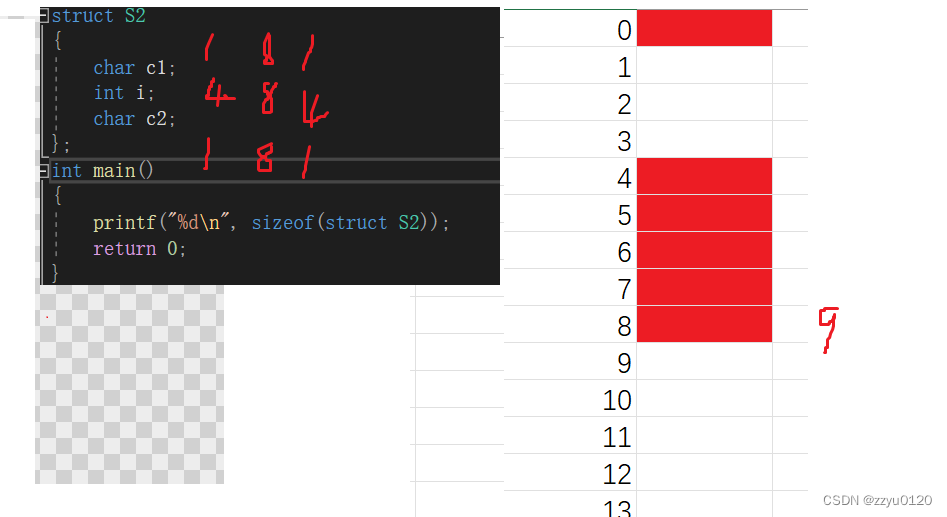
因为对齐数要是最大对齐数的整数倍,所以就是12
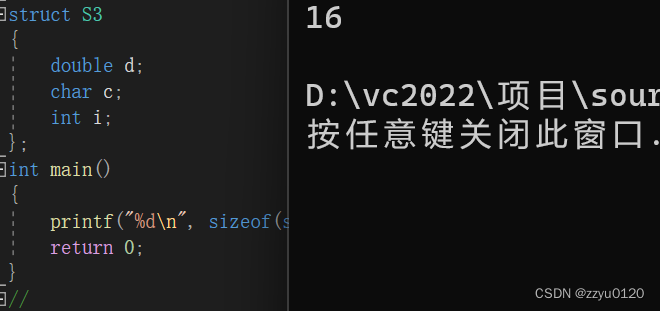
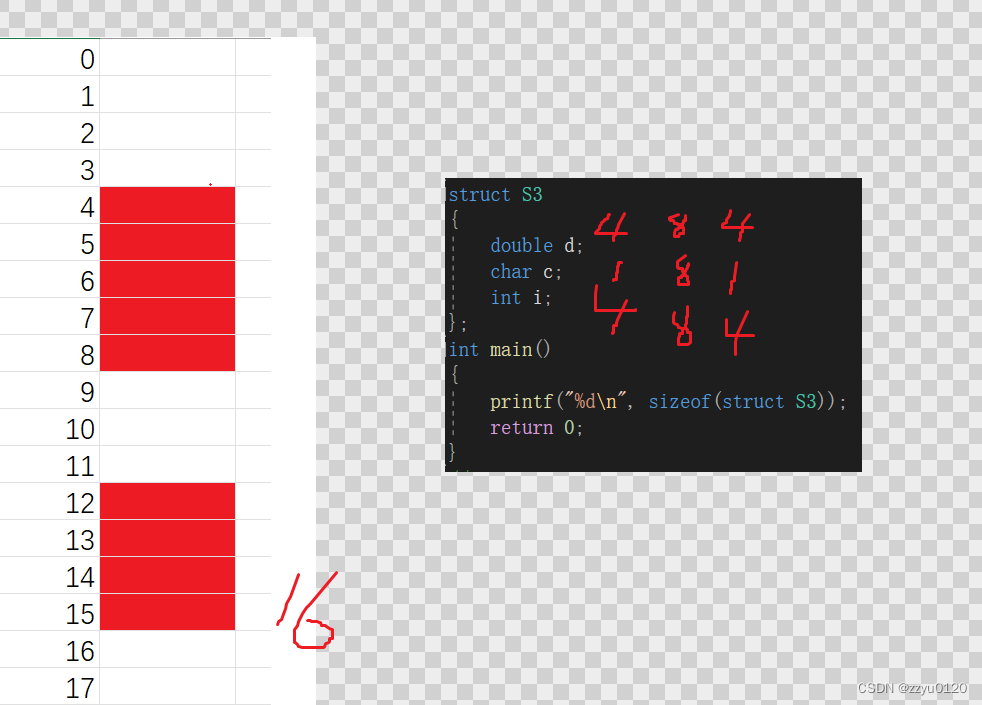
练习3
struct S3
{double d;char c;int i;
};
int main()
{printf("%d\n", sizeof(struct S3));return 0;
}
运行结果是
下面画图来解释以下原因:
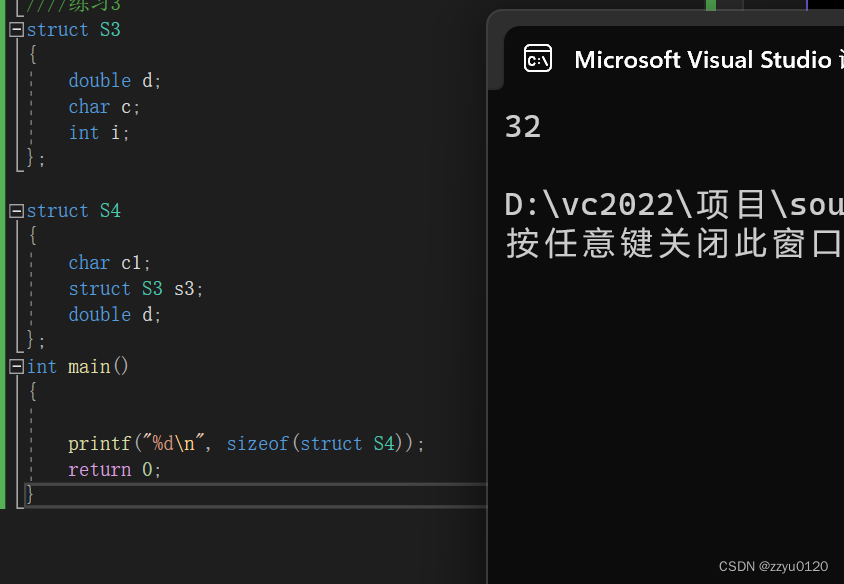
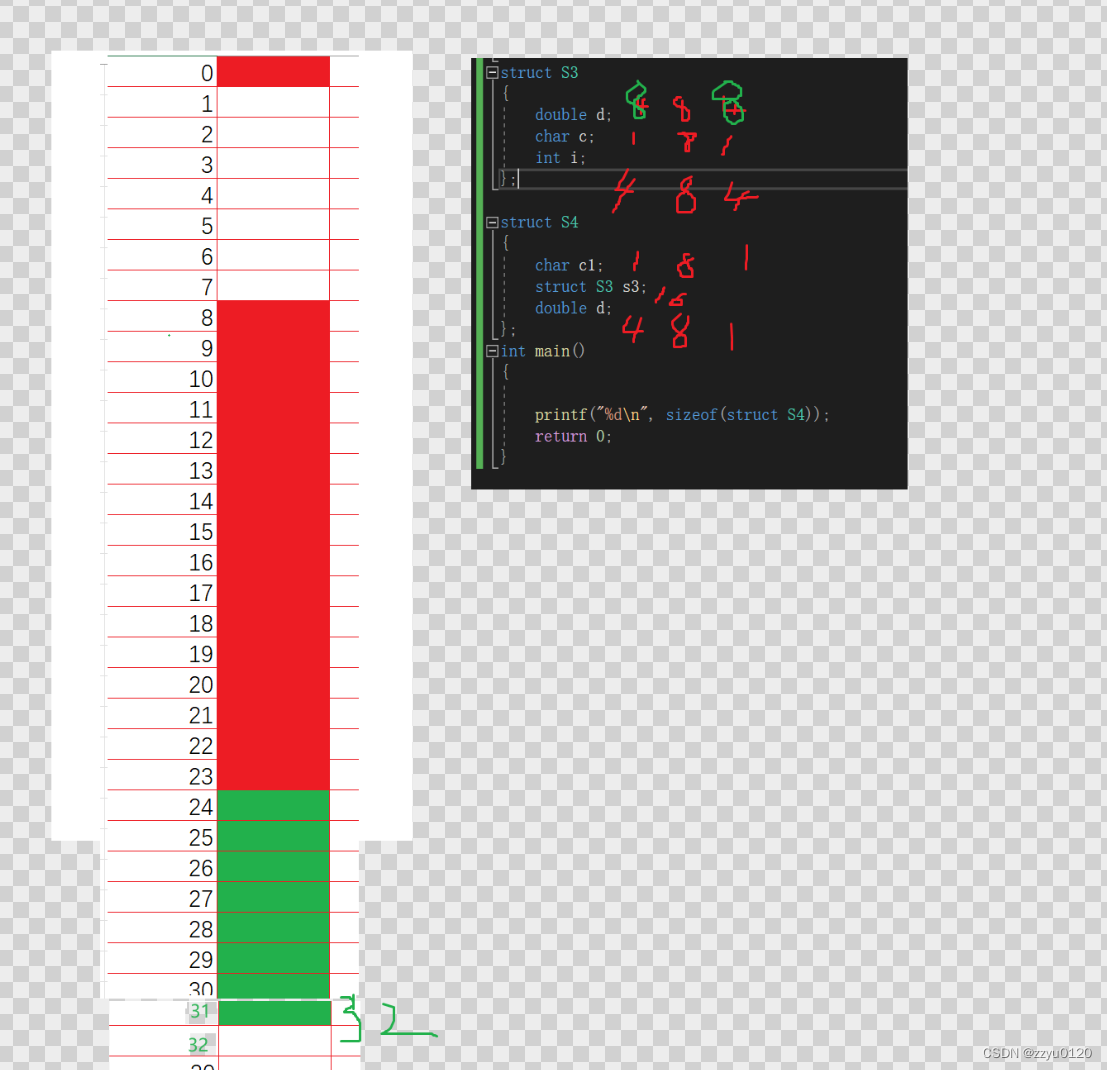
练习4(嵌套结构体的对齐数)
struct S3
{double d;char c;int i;
};struct S4
{char c1;struct S3 s3;double d;
};
int main()
{printf("%d\n", sizeof(struct S4));return 0;
}
运行结果
下面画图来解释以下原因:
4.2修改默认对齐数
可以使用
#pragam pack(1),设置默认对齐数为1
pragam pack()取消设置默认对齐数
五.结构体传参
struct S
{int data[1000];int num;
};
struct S s = {{1,2,3,4}, 1000};
//结构体传参
void print1(struct S s)
{printf("%d\n", s.num);
}
//结构体地址传参
void print2(struct S* ps)
{printf("%d\n", ps->num);
}
int main()
{print1(s); //传结构体print2(&s); //传地址return 0;
}
六.联合体
6.1联合体类型的声明
联合体的特点是所有成员共用同一块内存空间。所以联合体也叫:共用体。
给联合体其中⼀个成员赋值,其他成员的值也跟着变化。
//联合类型的声明
union Un
{char c;int i;
};
int main()
{//联合变量的定义union Un un = {0};//计算连个变量的⼤⼩printf("%d\n", sizeof(un));return 0;
}
运行结果:
4
6.2联合体的特点
联合的成员是共用同⼀块内存空间的,这样⼀个联合变量的大小,至少是最大成员的大小(因为联合至少得有能力保存最大的那个成员)。
代码
#include <stdio.h>
//联合类型的声明
union Un
{char c;int i;
};
int main()
{//联合变量的定义union Un un = {0};printf("%p\n", &(un.i));printf("%p\n", &(un.c));printf("%p\n", &un);return 0;
}
输出结果:
001AF85C
001AF85C
001AF85C
6.2计算联合体的大小
联合的大小至少是最⼤成员的大小。
当最大成员大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。
代码:
union Un1
{char c[5];int i;
};
union Un2
{short c[7];int i;
};
int main()
{//下⾯输出的结果是什么?printf("%d\n", sizeof(union Un1));printf("%d\n", sizeof(union Un2));return 0;
}
运行结果:
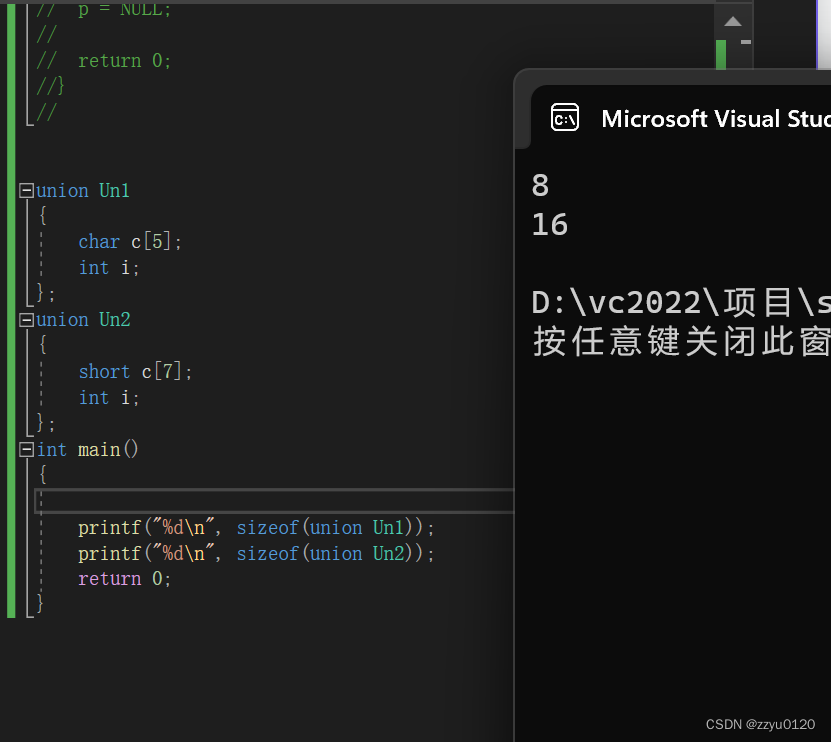
下面画图来解释以下原因:
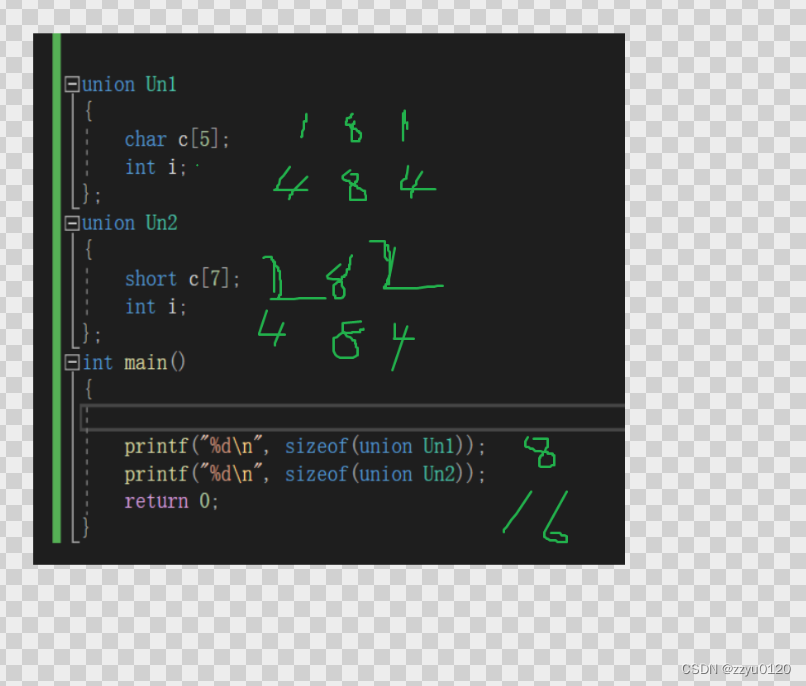
因为Un1的
char c[5]需要占用5个字节,5不是4的倍数,所以就是8个字节
Un2的char c[7]要占用14个字节,但是14不是结构第默认对齐数的最小公倍数,所以就是16
6.3用联合体判断大小端字节序
int check_sys()
{union{int i;char c;}un;un.i = 1;return un.c;
}
七.枚举类型
7.1枚举类型的声明
enum Day//星期
{Mon,Tues,Wed,Thur,Fri,Sat,Sun
};
enum Sex//性别
{MALE,FEMALE,SECRET
};
enum Color//颜⾊
{RED,GREEN,BLUE
};
1. 以上定义的 enum Day , enum Sex ,enum Color 都是枚举类型。
2. {}中的内容是枚举类型的可能取值,也叫 枚举常量 。
3. 这些可能取值都是有值的,默认从0开始,依次递增1,当然在声明枚举类型的时候也可以赋初值。
enum Color//颜⾊
{RED=2,GREEN=4,BLUE=8
};
7.2枚举的优点
- 增加代码的可读性和可维护性
- 和#define定义的标识符⽐较枚举有类型检查,更加严谨。
- 便于调试,预处理阶段会删除 #define 定义的符号
- 使用方便,一次可以定义多个常量
- 枚举常量是遵循作用域规则的,枚举声明在函数内,只能在函数内使用
7.3 枚举类型的使用
enum Color//颜⾊
{RED=1,GREEN=2,BLUE=4
};
enum Color clr = GREEN;
在C语言中是可以的,但是在C++是不行的,C++的类型(语法)检查比较严格。
文章到这里结束了!!!如果有错,请立刻指正,谢谢!!!
相关文章:

C语言结构体和位段
自定义类型:结构体及联合和枚举 一.结构体类型的声明1.1 结构体的概念1.2结构的声明1.3特殊的声明1.4结构体的自引用1.5可以使用typedef重命名 二.结构体变量的创建和初始化2.1结构体变量的初始化使用{}2.2初始化:定义变量的同时赋初值。2.3结构体嵌套及…...

【剑指offer|图解|数组】寻找文件副本 + 螺旋遍历二维数组
🌈个人主页:聆风吟 🔥系列专栏:数据结构、剑指offer每日一练 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. ⛳️寻找文件副本(题目难度:简单)1.1 题目1.2 示例1.3 限制1.4 解题思路一c代…...

Python核心编程之文件和输入输出
目录 一、文件对象 二、 文件内建函数[open()和file()] 1、工厂函数 file() 2、通用换行符支持(UNS)...
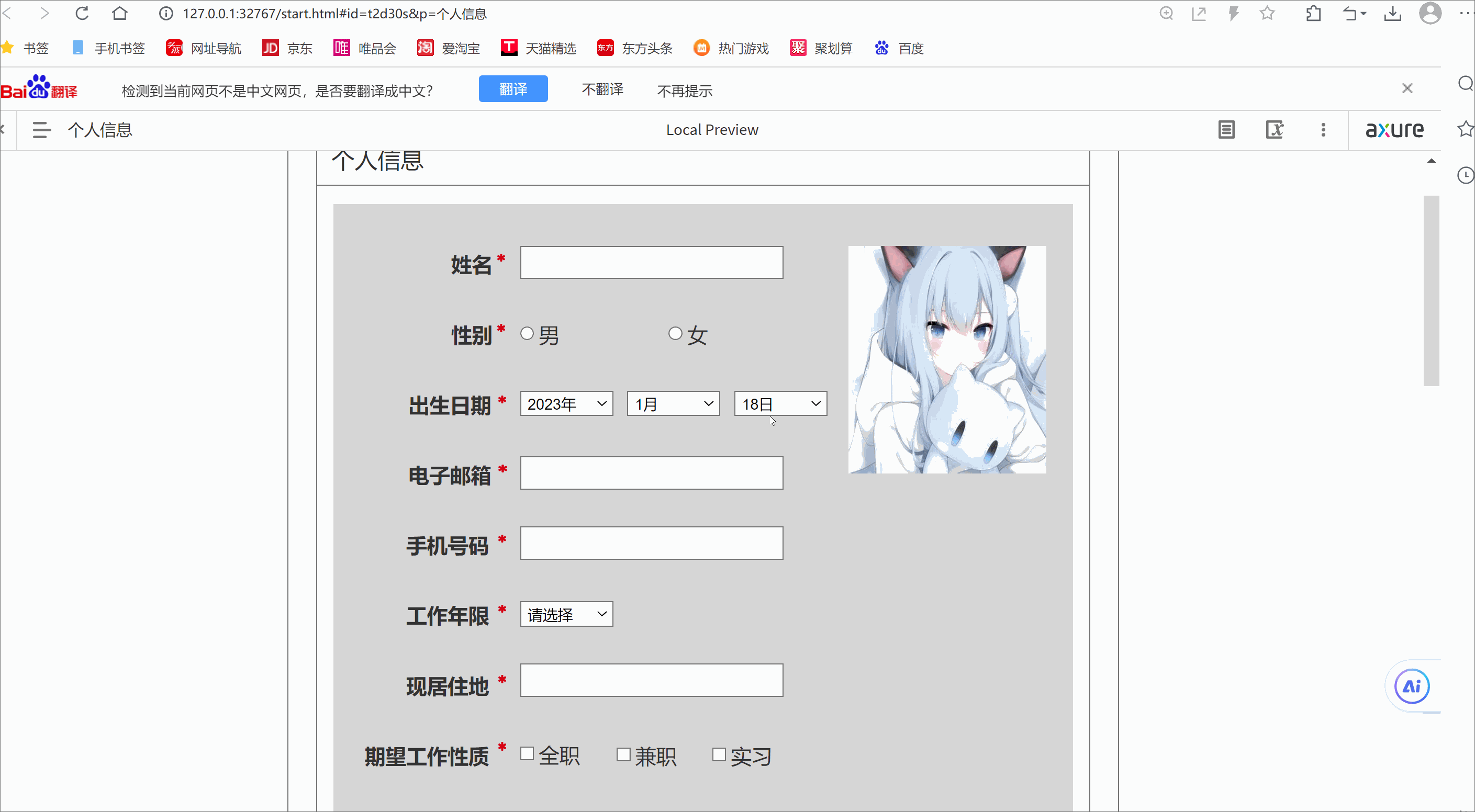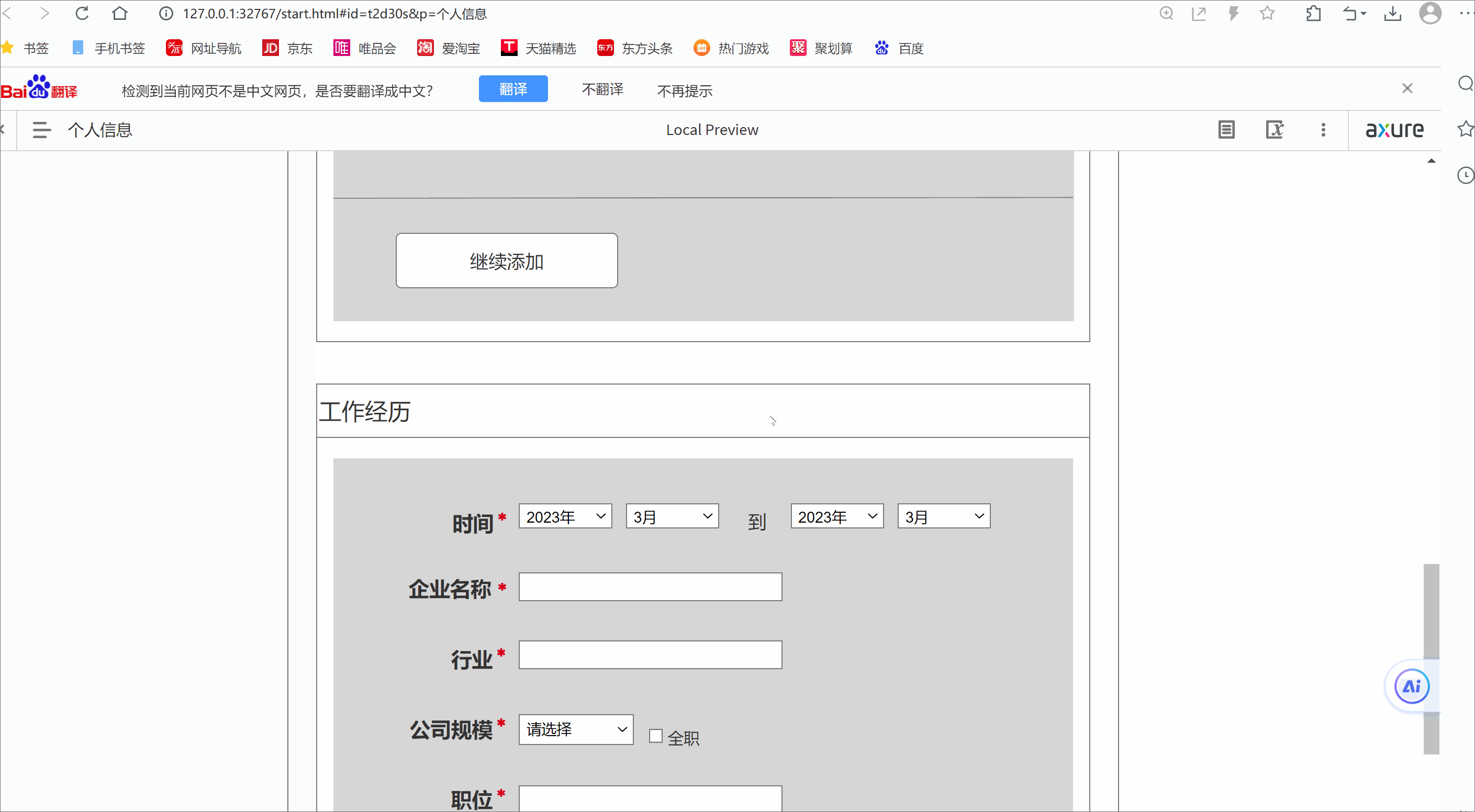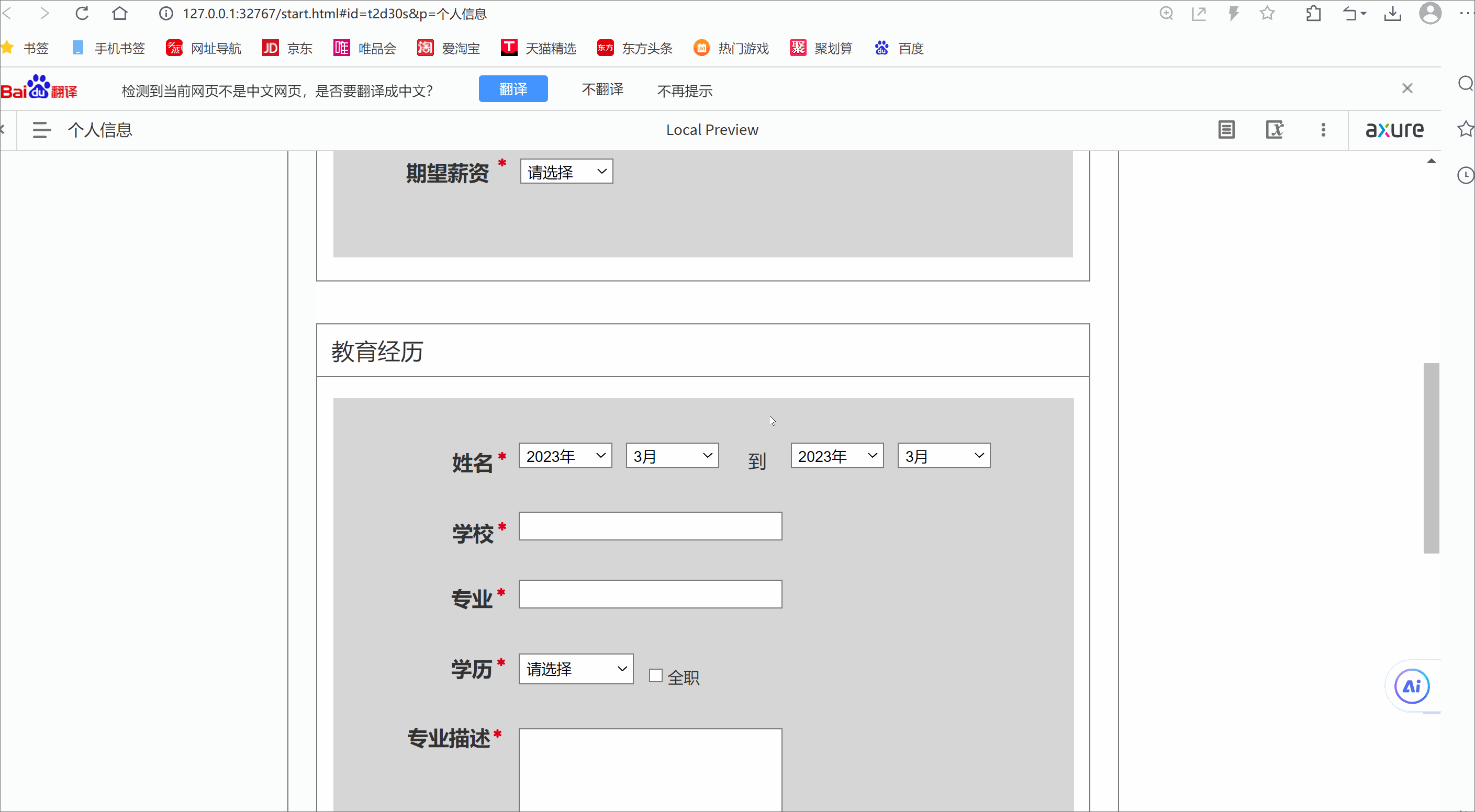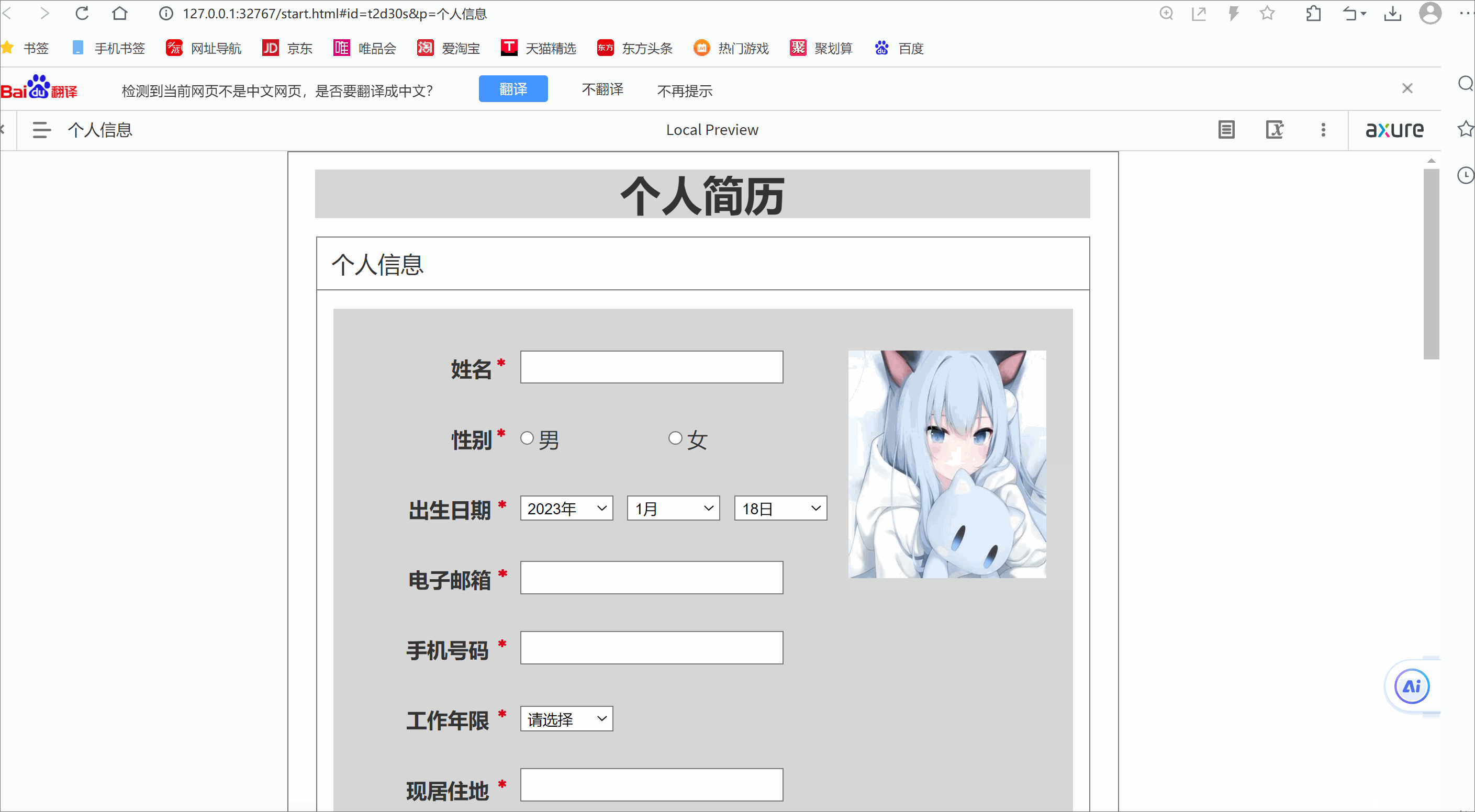
Axure 9基本元件,表单及表格元件简介,表单案例
目录 一.基本元件 1.元件基本介绍 2.基本元件的使用 二.表单及表格元件 三.表单案例 四.简单简历绘制 一.基本元件 1.元件基本介绍 概述 - 在Axure RP中,元件是**构建原型图的基础模块**。 将元件从元件库里拖拽到画布中,即可添加元件到你的原型…...
ARM I2C通信
1.概念 I2C总线是PHLIPS公司在八十年代初推出的一种串行的半双工同步总线,主要用于连接整体电路2.IIC总线硬件连接 1.IIC总线支持多主机多从机,但是在实际开发过程中,大多数采用单主机多从机模式 2.挂接到IIC总线上,每个从机设备都…...
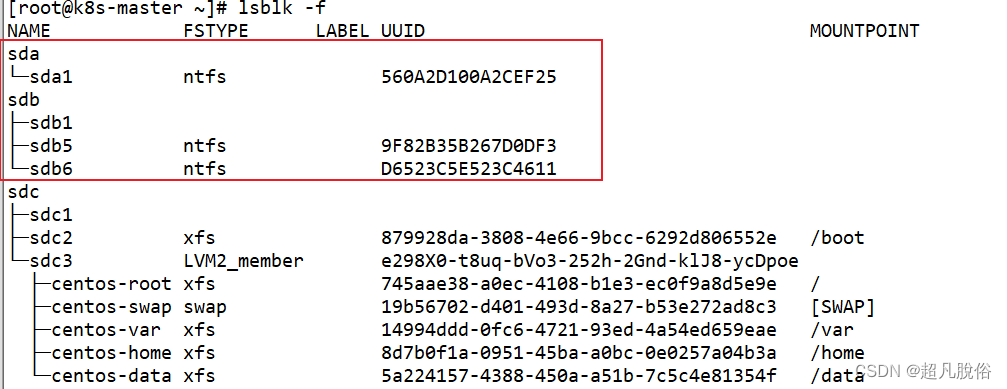
Cent OS7 磁盘挂载:扩展存储空间和自动挂载
文章目录 (1)概述(2)查看磁盘使用情况(3)VMware虚拟机挂载磁盘(4)物理机磁盘挂载(5)ntfs硬盘处理 (1)概述 在Linux系统中,…...
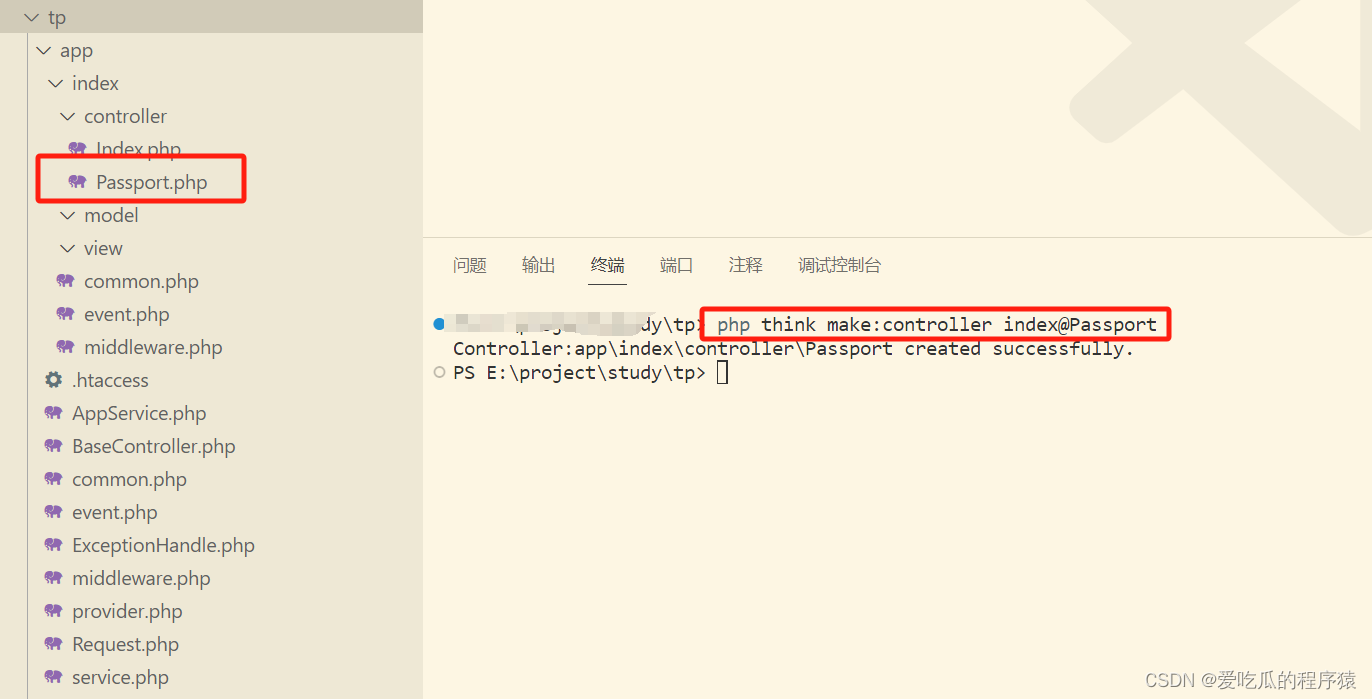
《使用ThinkPHP6开发项目》 - 创建应用
《使用ThinkPHP6开发项目》 - 安装ThinkPHP框架-CSDN博客 《使用ThinkPHP6开发项目》 - 设置项目环境变量-CSDN博客 《使用ThinkPHP6开发项目》 - 项目使用多应用开发-CSDN博客 根据前面的步骤,我们现在就可以开发我们的项目开发了,根据项目开发的需要…...

SpringBoot进行自然语言处理,利用Hanlp进行文本情感分析
. # 📑前言 本文主要是SpringBoot进行自然语言处理,利用Hanlp进行文本情感分析,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风…...
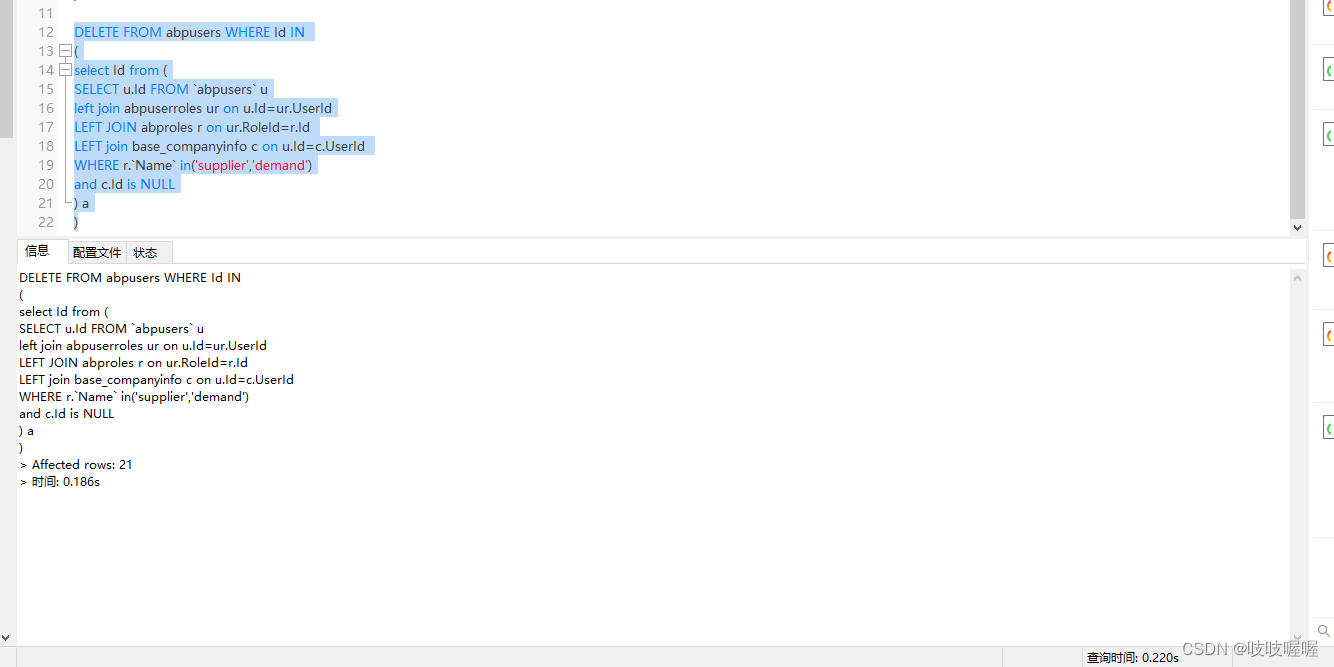
MySQL 报错 You can‘t specify target table for update in FROM clause解决办法
You can’t specify target table for update in FROM clause 其含义是:不能在同一表中查询的数据作为同一表的更新数 单独执行复合查询是正常的,如下: 但是当执行子查询删除命令时,报如下错误 DELETE FROM abpusers WHERE Id I…...

Linux中使用podman管理容器
本章主要介绍使用podman管理容器 了解什么是容器,容器和镜像的关系安装和配置podman拉取和删除镜像给镜像打标签导出和导入镜像创建和删除镜像数据卷的使用管理容器的命令使用普通用户管理容器 对于初学者来说,不太容易理解什么是容器,这里…...

飞天使-linux操作的一些技巧与知识点3-http的工作原理
文章目录 http工作原理nginx的正向代理和反向代理的区别一个小技巧dig 命令巧用 http工作原理 http1.0 协议 使用的是短连接,建立一次tcp连接,发起一次http的请求,结束,tcp断开 http1.1 协议使用的是长连接,建立一次tc…...
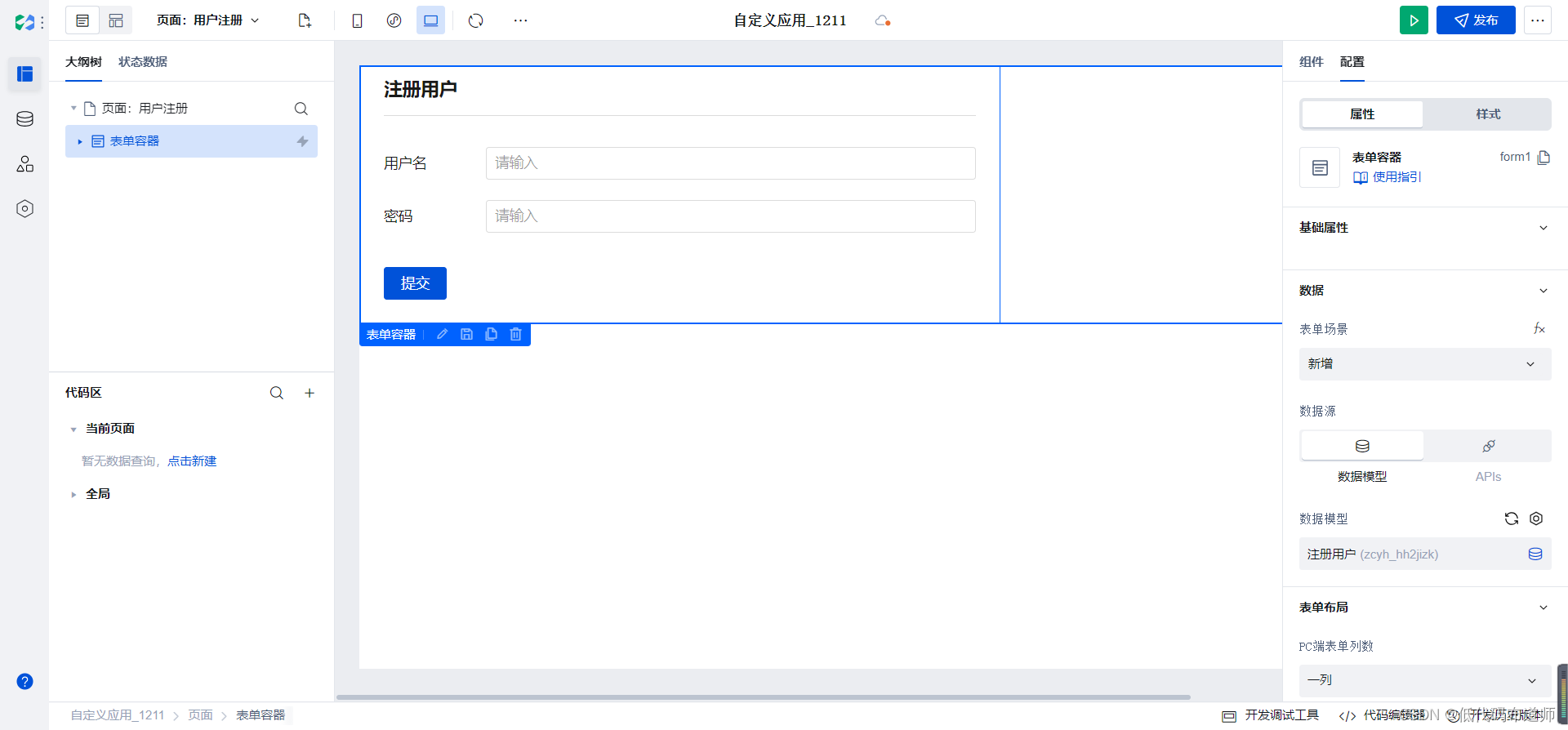
微搭低代码实现登录注册功能
目录 1 创建用户数据源2 实现登录逻辑3 搭建登录页面4 设置登录框5 实现登录的逻辑6 用户注册总结 原来产品在创建应用的时候可以创建模型应用,模型应用对应我们小程序的后端。最新的更新已经将模型应用的能力下线,那我们不得不自己实现一下后端的逻辑。…...
使用Cobalt Srike制作钓鱼文件
钓鱼 钓鱼文件是一种常见的网络攻击手段,旨在欺骗用户,诱使他们点击恶意链接、下载恶意附件或提供敏感信息。钓鱼文件的概念是通过伪装成合法、可信的文件或链接来欺骗受害者,使其相信文件或链接的来源是可信的,从而促使他们采取…...

任意文件读取漏洞
使用方法php://filter/readconvert.base64-encode/resourcexxx 任意文件读取漏洞 php://filter/readconvert.base64-encode/resourceflag 在url后边接上 以base64的编码形式 读取flag里面的内容 php://filter/readconvert.base64encode/resourceflag 用kali来解码 创建一个文…...

一个文件下png,jpg,jpeg,bmp,xml,json,txt文件名称排序命名
#utf-8 #authors 会飞的渔WZH #time:2023-12-13 import os# 要修改的图像所在的文件夹路径 root_path rD:\images\lines2\3 # 要修改的图像所在的文件夹路径filelist os.listdir(root_path) #遍历文件夹 print(len(filelist)) i0for item in filelist:if item.endswith(.…...
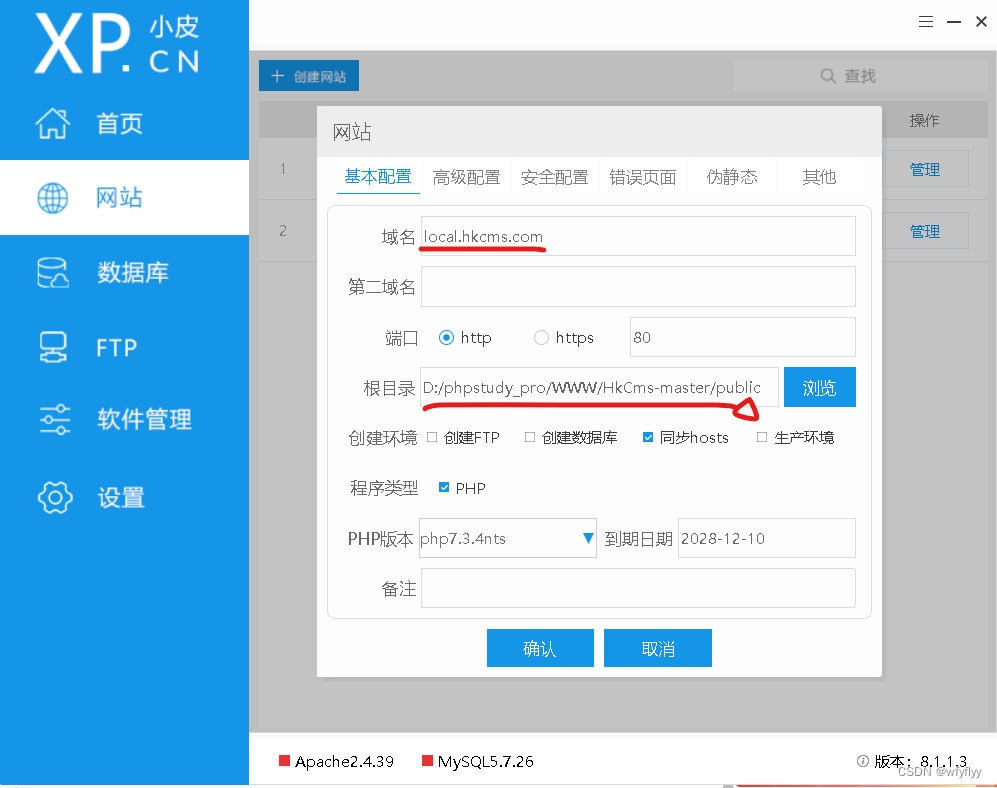
phpstudy小皮(PHP集成环境)下载及使用
下载 https://www.xp.cn/download.html直接官网下载即可,下载完解压是个.exe程序,直接点击安装就可以,它会自动在D盘目录为D:\phpstudy_pro 使用 phpMyAdmin是集成的数据库可视化,这里需要下载一下,在软件管理-》网站程…...

[BUG记录]UART占用CPUload过高问题
目录 关键词平台说明一、背景二、根本原因三、措施 关键词 嵌入式、C语言、autosar、TDA4 平台说明 项目ValueOSautosar OSautosar厂商vector芯片厂商TI编程语言C,C编译器HighTec (GCC) 一、背景 在基于TDA4开发的域控中使用到了UART打印debug信息,不…...

Flutter常用命令
一、环境安装 flutter --version 查看当前安装的flutter 版本 flutter upgrade 升级当前的flutter 版本 flutter doctor 检查环境安装是否完成 二、项目编译运行 flutter clean 清空build目录 flutter pub get 获取pub插件包 flutter run --设备名称 运行项目到指定设…...
:引用计数、共享指针、缓冲区管理)
【C++】POCO学习总结(十四):引用计数、共享指针、缓冲区管理
【C】郭老二博文之:C目录 1、Poco::AutoPtr 智能指针 1.1 说明 Poco::AutoPtr是一个含有引用计数的“智能”指针模版。 Poco::AutoPtr用于支持引用计数的类实例化。支持引用计数的类需要有以下要求: 维护一个引用计数(在创建时初始化为1)实现void du…...

Python之禅
import this 这是 Python 社区中著名的 "The Zen of Python"(Python之禅)文档,由 Python 创始人之一的 Tim Peters 撰写。这个文档包含了一系列关于编程和代码设计哲学的原则,以指导 Python 社区的开发者。以下是这些原…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...