参数学习——糖果问题(人工智能期末复习)
之前看了好久都不知道这题咋写,后来看了这篇机器智能-高频问题:糖果问题,大概看明白了,其实主要围绕着这两个公式

光看公式也看不懂,还是要结合题目来
己知有草莓味和酸橙味两种类型的糖果,分别放入5种不同的包装之中,
h1包装中100%是草莓味
h2包装中75%是草莓味25%是酸橙味
h3包装中50%是草莓味50%是酸橙味
h4包装中25%是草莓味75%是酸橙味
h5包装中100%是酸橙味
假定h1,h2… h5的先验分布概率为<0.1,0.2,0.4,0.2,0.1>,每次拿出糖果是相互独立的且不影响袋子里面糖果的比例,试回答下列问题:
(1)假定拿出的2个糖果都是草莓味,请分别计算每拿出一个糖果后h1到h5的概率值;
(2)在(1)的基础上计算下个糖果为草莓味,酸橙味的概率。
解:
(1)
- 拿出的第一个是草莓味
分别计算拿出的第一个是草莓味(d)的前提下从hi包装拿出的概率
P(h1|d) = 0.1×1×a=0.1a
P(h2|d) = 0.2×0.75×a=0.15a
P(h3|d) = 0.4×0.5×a=0.2a
P(h4|d) = 0.2×0.25×a=0.05a
P(h5|d) = 0.1×0×a=0
进行归一化:0.1a+0.15a+0.2a+0.05a+0=1 → a=2
因此
P(h1|d) = 0.1×1×a=0.2
P(h2|d) = 0.2×0.75×a=0.3
P(h3|d) = 0.4×0.5×a=0.4
P(h4|d) = 0.2×0.25×a=0.1
P(h5|d) = 0.1×0×a=0 - 拿出的第二个还是草莓味
P(h1|d) = 0.1×1×1×a=0.1a
P(h2|d) = 0.2×0.75×0.75×a=0.1125a
P(h3|d) = 0.4×0.5×0.5×a=0.1a
P(h4|d) = 0.2×0.25×0.25×a=0.0125a
P(h5|d) = 0.1×0×0×a=0
进行归一化:0.1a+0.1125a+0.1a+0.0125a+0=1 → a=40/13
所以
P(h1|d) = 0.1×1×1×a=0.3
P(h2|d) = 0.2×0.75×0.75×a=0.346
P(h3|d) = 0.4×0.5×0.5×a=0.3
P(h4|d) = 0.2×0.25×0.25×a=0.038
P(h5|d) = 0.1×0×0×a=0
(2)在第一题的基础上我们已经计算出了拿的包装是hi的概率,这一问就利用P(hi|d)来预测下一个糖的概率
在已知拿出了前两个都是草莓味(d)的前提下,预测下一个糖是草莓味(X)的概率
P(X|d) = ∑P(X|hi)P(hi|d) = 1×0.3+0.75×0.346+0.5×0.3+0.25×0.038+0 = 0.719
在已知拿出了前两个都是草莓味(d)的前提下,预测下一个糖是酸橙味(Y)的概率
P(Y|d) = ∑P(Y|hi)P(hi|d) = 0+0.25×0.346+0.5×0.3+0.75×0.038+0 = 0.265
再换一题试试看
已知有5种包含的糖果:
h1:草莓味100%
h2:草莓味80%、酸橙味20%
h3:草莓味50%、酸橙味50%
h4:草莓味20%、酸橙80%
h5:酸橙味100%
5种包装的先验概率分别是10%、20%、30%、10%、30%
假定依次从袋子里拿出3个糖果分别是草莓味、酸橙味、酸橙味包装内的糖果数量是无穷多的,回答下列问题
1)分别计算该袋子为h1到h5的概率;
2)下一个糖果是草莓味和酸橙味的概率
(1)
- 拿出的第一个是草莓味
P(h1|d) = 0.1×1×a=0.1a
P(h2|d) = 0.2×0.8×a=0.16a
P(h3|d) = 0.3×0.5×a=0.15a
P(h4|d) = 0.1×0.2×a=0.02a
P(h5|d) = 0.3×0×a=0
进行归一化:0.1a+0.16a+0.15a+0.02a+0=1 → a=100/43
因此
P(h1|d) = 0.1×1×a=0.23
P(h2|d) = 0.2×0.8×a=0.37
P(h3|d) = 0.3×0.5×a=0.35
P(h4|d) = 0.1×0.2×a=0.05
P(h5|d) = 0.3×0×a=0 - 拿出的第二个是酸橙味
P(h1|d) = 0.1×1×0×a=0
P(h2|d) = 0.2×0.8×0.2×a=0.032a
P(h3|d) = 0.3×0.5×0.5×a=0.075a
P(h4|d) = 0.1×0.2×0.8×a=0.016a
P(h5|d) = 0.3×0×1×a=0
进行归一化:0+0.032a+0.075a+0.016a+0=1 → a=1000/123
所以
P(h1|d) = 0.1×1×0×a=0
P(h2|d) = 0.2×0.8×0.2×a=0.26
P(h3|d) = 0.3×0.5×0.5×a=0.61
P(h4|d) = 0.1×0.2×0.8×a=0.13
P(h5|d) = 0.3×0×1×a=0 - 拿出的第三个还是酸橙味
P(h1|d) = 0.1×1×0×0×a=0
P(h2|d) = 0.2×0.8×0.2×0.2×a=0.0064a
P(h3|d) = 0.3×0.5×0.5×0.5×a=0.0375a
P(h4|d) = 0.1×0.2×0.8×0.8×a=0.0128a
P(h5|d) = 0.3×0×1×1×a=0
进行归一化:0+0.0064a+0.0375a+0.0128a+0=1 → a=10000/567
所以
P(h1|d) = 0.1×1×0×0×a=0
P(h2|d) = 0.2×0.8×0.2×0.2×a=0.11
P(h3|d) = 0.3×0.5×0.5×0.5×a=0.66
P(h4|d) = 0.1×0.2×0.8×0.8×a=0.23
P(h5|d) = 0.3×0×1×1×a=0
(2)
下一个糖是草莓味(X)的概率
P(X|d) = ∑P(X|hi)P(hi|d) = 0.8×0.11+0.5×0.66+0.2×0.23 = 0.464
下一个糖是酸橙味(Y)的概率
P(Y|d) = ∑P(Y|hi)P(hi|d) = 0.2×0.11+0.5×0.66+0.8×0.23 = 0.536
相关文章:

参数学习——糖果问题(人工智能期末复习)
之前看了好久都不知道这题咋写,后来看了这篇机器智能-高频问题:糖果问题,大概看明白了,其实主要围绕着这两个公式 光看公式也看不懂,还是要结合题目来 己知有草莓味和酸橙味两种类型的糖果,分别放入5种不同…...
【深度学习】注意力机制(六)
本文介绍一些注意力机制的实现,包括MobileVITv1/MobileVITv2/DAT/CrossFormer/MOA。 【深度学习】注意力机制(一) 【深度学习】注意力机制(二) 【深度学习】注意力机制(三) 【深度学习】注意…...
螺旋矩阵算法(leetcode第59题)
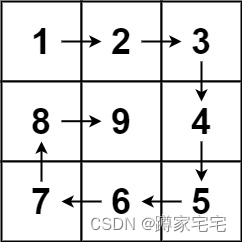
题目描述: 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。示例 1:输入:n 3 输出:[[1,2,3],[8,9,4],[7,6,5]] 示例 2:输入&#…...
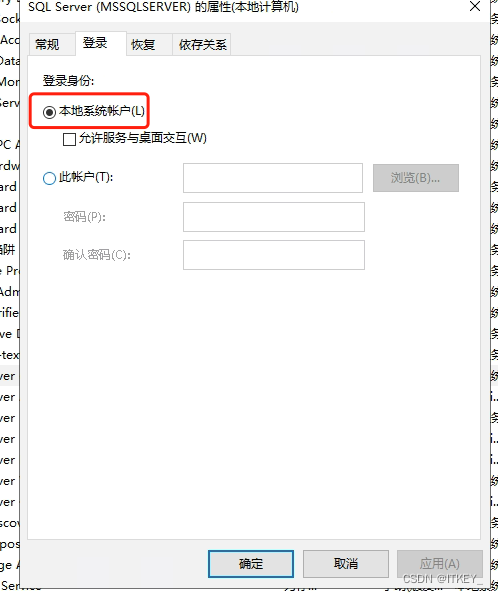
SQL Server 服务启动报错:错误1069:由于登录失败而无法启动服务
现象 服务器异常关机以后,SQL Server服务无法启动了。 启动服务时报错: 错误1069:由于登录失败而无法启动服务 解决办法 我的电脑–控制面板–管理工具–服务–右键MSSQLSERVER–属性–登录–登陆身份–选择"本地系统帐户" 设置完成后&am…...

“ABCD“[(int)qrand() % 4]作用
ABCD[(int)qrand() % 4] 作用 具体来说: qrand() 是一个函数,通常在C中用于生成一个随机整数。% 4 会取 qrand() 生成的随机数除以4的余数。因为4只有四个不同的余数(0, 1, 2, 3),所以这实际上会生成一个0到3之间的随…...

Vue2面试题:说一下组件通信有哪些方式?
父传子 1、自定义属性 props:在父组件中,给子组件绑定一个自定义属性,在子组件中,通过props进行接收 2、$parent:直接访问父组件实例的属性和方法 3、$attrs:在父组件中,给子组件绑定一个自定义…...
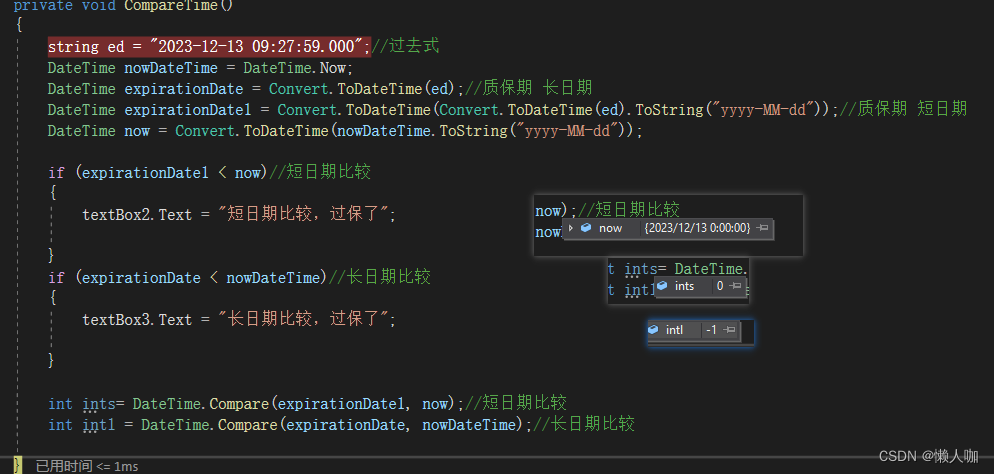
C# 两个日期比较大小
文章目录 C# 两个日期比较大小直接比较大小工具类DateTime.Compare C# 两个日期比较大小 直接比较大小 string ed "2023-12-13 09:27:59.000";//过去式DateTime nowDateTime DateTime.Now;DateTime expirationDate Convert.ToDateTime(ed);//质保期 长日期DateT…...
路由基本原理
目录 一、路由器概述 二、路由器的工作原理 三、路由表的形成 四、路由配置 1.连接设备 2.进入系统模式 3.进入接口模式 4.配置网络 5.下一跳的设置 6.设置浮动路由 7.设置默认路由 一、路由器概述 路由器(Router)是一种用于连接不同网络或子…...

配置本地端口镜像示例
镜像概念 定义 镜像是指将指定源的报文复制一份到目的端口。指定源被称为镜像源,目的端口被称为观察端口,复制的报文被称为镜像报文。 镜像可以在不影响设备对原始报文正常处理的情况下,将其复制一份,并通过观察端口发送给监控…...
使用FluentAvalonia组件库快速完成Avalonia前端开发
前言 工欲善其事必先利其器,前面我们花了几篇文章介绍了Avalonia框架以及如何在Avalonia框架下面使用PrismAvalonia完成MVV模式的开发。今天我们将介绍一款重磅级的Avalonia前端组件库,里面封装了我们开发中常用的组件,这样就不用我们自己再写组件了。专注业务功能开发,提…...

JAVA实体类集合该如何去重?
JAVA实体类集合该如何去重? 最近在工作中经常遇到需要去重的需求,所以特意系统的来梳理一下 有目录,不迷路 JAVA实体类集合该如何去重?单元素去重方法一:利用Set去重方法二:利用java 8的stream写法…...

修改Element UI可清空Input的样式
如图所示,修改Input右侧的清空按钮位置: <el-input class"create-catalog-ipt"placeholder"请输入相关章节标题"v-model"currentCatalogTitle"clearable /> // SCSS环境 ::v-deep {.create-catalog-ipt {input {he…...
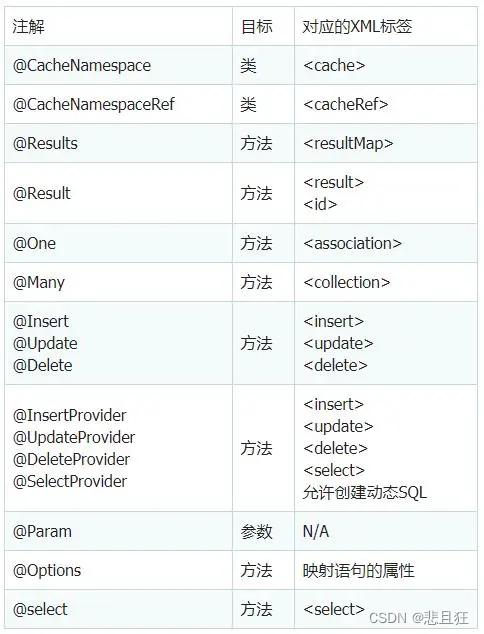
Java常用注解
文章目录 第一章、Java注解与元数据1.1)元数据与注解概念介绍1.2)Java注解的作用和使用1.3)注解的分类 第二章、Mybatis框架常用注解2.1)Mybatis注解概览2.2)常用注解MapperScanMapperSelectInsertUpdateDeleteParam结…...

golang实现同步阻塞、同步非阻塞、异步非阻塞IO模型
一、同步阻塞IO模型TCP和HTTP示例 同步阻塞IO符合我们的直觉认知,应用程序从TCP连接接收数据缓冲区接受数据,如果没有数据就等待——此处就是阻塞,如果有数据需要把数据从内核空间读取到用户空间——此处就是同步。 在Go语言中进行同步阻塞IO编程TCP交互,可以使用标准库中…...
java SSM教师工作量管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM 教师工作量管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要…...
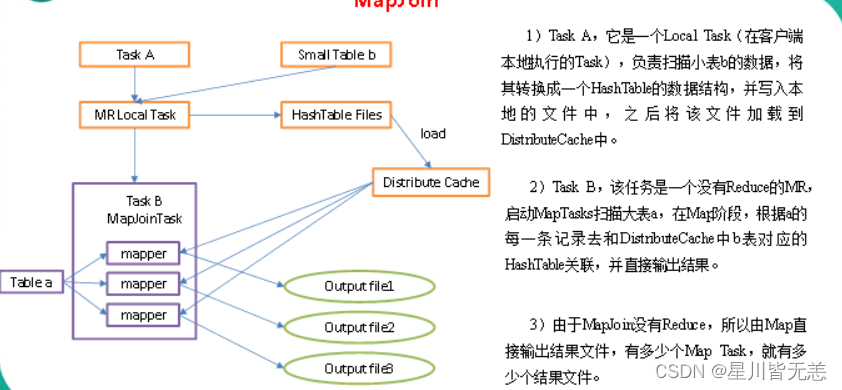
大数据技术之Hive(超级详细)
第1章 Hive入门 1.1 什么是Hive Hive:由Facebook开源用于解决海量结构化日志的数据统计。 Hive是基于Hadoop的一个数据仓库工具,可以将结构化的数据文件映射为一张表,并提供类SQL查询功能。 本质是:将HQL转化成MapReduce程序 …...

NVMe over Fabrics with SPDK with iRDMA总结 - 1
1.0 Introduction简介 NVM Express* (NVMe*) drives are high-speed, low-latency, solid-state drives (SSDs), that connect over the server Peripheral Component Interconnect Express* (PCIe*) bus. NVM Express* (NVMe*) 硬盘是高速、低延迟的固态硬盘 (SSD),通过服…...
)
【PTA刷题】求链式线性表的倒数第K项(代码+详解)
文章目录 题目代码详解 题目 给定一系列正整数,请设计一个尽可能高效的算法,查找倒数第K个位置上的数字。 输入格式: 输入首先给出一个正整数K,随后是若干非负整数,最后以一个负整数表示结尾(该负数不算在序列内&#…...

VSCode 创建工作区,多文件夹终端切换
VSCode 创建工作区的好处有以下几点: 项目结构清晰:每个工作区都有自己的文件夹结构,可以更好地组织和管理项目文件。版本控制:VSCode 支持多种版本控制系统,如Git,可以在工作区内进行代码的版本管理。插件…...
)
高阶函数(js的问题)
(1)函数可以作为参数被传递 (2)函数可以作为返回值输出 4-1.函数作为参数传递 Array.prototype.sort方法: var array [10,5,12,3];array.sort();//array:[10,12,3,5]//如代码那样,排序的结果并不是我们想要…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
