高阶函数(js的问题)
(1)函数可以作为参数被传递
(2)函数可以作为返回值输出
4-1.函数作为参数传递
Array.prototype.sort方法:
var array = ['10','5','12','3'];array.sort();//array:['10','12','3','5']//如代码那样,排序的结果并不是我们想要的,这与sort函数的比较规则有关系array.sort(function(a,b){return a-b;});//array:['3','5','10','12']传入一个比较的函数,就可以按照数字大小的规则进行正确的比较了。4-2.函数作为返回值输出
var getSingle = function ( fn ) {var ret;return function () {return ret || ( ret = fn.apply( this, arguments ) );};};4-3.函数作为参数被传递并且返回另一个函数
var getScript = getSingle(function(){return document.createElement( 'script' );});var script1 = getScript();var script2 = getScript();alert ( script1 === script2 ); // 输出:true4-4.高阶函数应用
(1)高阶函数实现AOP
AOP(面向切面编程)的主要作用是把一些跟核心业务逻辑模块无关的功能抽离出来,这些业务逻辑无关的功能包括日志统计、控制安全、异常处理等。把这些功能抽离出来之后,再通过“动态织入”的方式掺入业务逻辑模块中。
下面代码通过扩展Function.prototype来实现把一个函数“动态织入”
Function.prototype.before = function( beforefn ){var __self = this; // 保存原函数的引用return function(){ // 返回包含了原函数和新函数的"代理"函数beforefn.apply( this, arguments ); // 执行新函数,修正thisreturn __self.apply( this, arguments ); // 执行原函数}};Function.prototype.after = function( afterfn ){var __self = this;return function(){var ret = __self.apply( this, arguments );afterfn.apply( this, arguments );return ret;}};var func = function(){console.log( 2 );};func = func.before(function(){console.log( 1 );}).after(function(){console.log( 3 );});func();
(2)柯里化
一个currying函数首先会接受一些参数,接受了这些参数之后,该函数不会立即求值,而是继续返回另外一个函数,刚才传入的参数在函数形成的闭包中被保存了下来。待到函数真正需要求值的时候,之前传入的所有参数都会一次性用于求值。
一个经典的柯里化:
function curry(fn){var arr1 = Array.prototype.slice.call(arguments,1);return function(){var arg2 = Array.prototype.slice.call(arguments);var array = arr1.concat(arr2);return fn.apply(null,array);}}
不断累积的柯里化:
var currying = function( fn ){var args = [];//外层函数变量:用来累积return function(){if ( arguments.length === 0 ){return fn.apply( this, args );}else{[].push.apply( args, arguments );return arguments.callee;}}};(3)uncurrying
在javascript中,当我们调用对象的某个方法时,其实不用关心对象原本是否被设计为拥有这个方法,这是动态类型语言的特点,也就是常说的鸭子类型思想。
同理,一个对象也未必只能使用它自己的方法,其实可以借用原本不属于他的方法: call apply
Function.prototype.uncurrying = function () {var self = this;return function() {var obj = Array.prototype.shift.call( arguments );return self.apply( obj, arguments );};};var push = Array.prototype.push.uncurrying();
var obj = {"length": 1,"0": 1
};push( obj, 2 );//将2使用push的方法作用到obj上
console.log( obj ); // 输出:{0: 1, 1: 2, length: 2}
相关文章:
)
高阶函数(js的问题)
(1)函数可以作为参数被传递 (2)函数可以作为返回值输出 4-1.函数作为参数传递 Array.prototype.sort方法: var array [10,5,12,3];array.sort();//array:[10,12,3,5]//如代码那样,排序的结果并不是我们想要…...

android-android源码目录
android源码目录 Android.bp art bionic bootable bootstrap.bash build build.sh compatibility cts dalvik developers development device external frameworks: Android 系统的核心框架代码av: 该目录包含与音视频相关的框架和库,如音频解码器、视频编码器、多…...

Json格式化
Json格式化 大家好,我是微赚淘客机器人的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! Json格式化:让数据更亮眼,解密Json的奇妙世界 在现代Web开发中,Json(JavaScript Object N…...

数据可视化设计:让数据故事更有说服力
写在开头 在数字化的时代,数据如同一把锁住的宝剑,等待我们挥舞。然而,唯有通过巧妙运用数据可视化的原则和技术,我们才能真正解锁数据的力量,创造出令人信服的数据故事。本文将深入研究数据可视化设计的奥秘,揭示其中的魔法,让你在数据的海洋中游刃有余,用数据的语言…...

java面试题-Spring事务以及@Transactional注解详解
远离八股文,面试大白话,通俗且易懂 看完后试着用自己的话复述出来。有问题请指出,有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来,大家一起解决。 java面试题汇总-目录-持续更新中 对于这个面试中高频问到…...

ARM流水灯
.text .global _start _start: LED1 1.RCC时钟使能GPIOE RCC_MP_AHB4ENSETR[4]->1 LDR R0,0x50000a28 LDR R1,[R0] ORR R1,R1,#(0x1<<4) STR R1,[R0] 2.设置PE10为输出模式 GPIOE_MODER[21:20]->01 先清0 LDR R0,0x50006000 LDR R1,[R0] BIC R1,R1,#(0x3<&…...

docker-compose单机容器编排
Dockerfile:先配置好文件,然后build,镜像-------->容器。 docker-conpose 既可以基于dockerfile,也可以基于镜像,一键式拉起镜像和容器。 docker-compose核心就是yml文件,可以定义容器的一切。通过yml配置,直接运行…...

matlab信号分选系统算法-完整算法结构
matlab信号分选系统算法 针对得到的脉冲流PDW进行信号分选,包括重频恒定、重频抖动、重频参差和重频滑变四种脉间调制类型。 这里我们先进行数据的仿真,后续边仿真边分享思路:首先根据信号类型,分别产生重频恒定、重频抖动、重…...
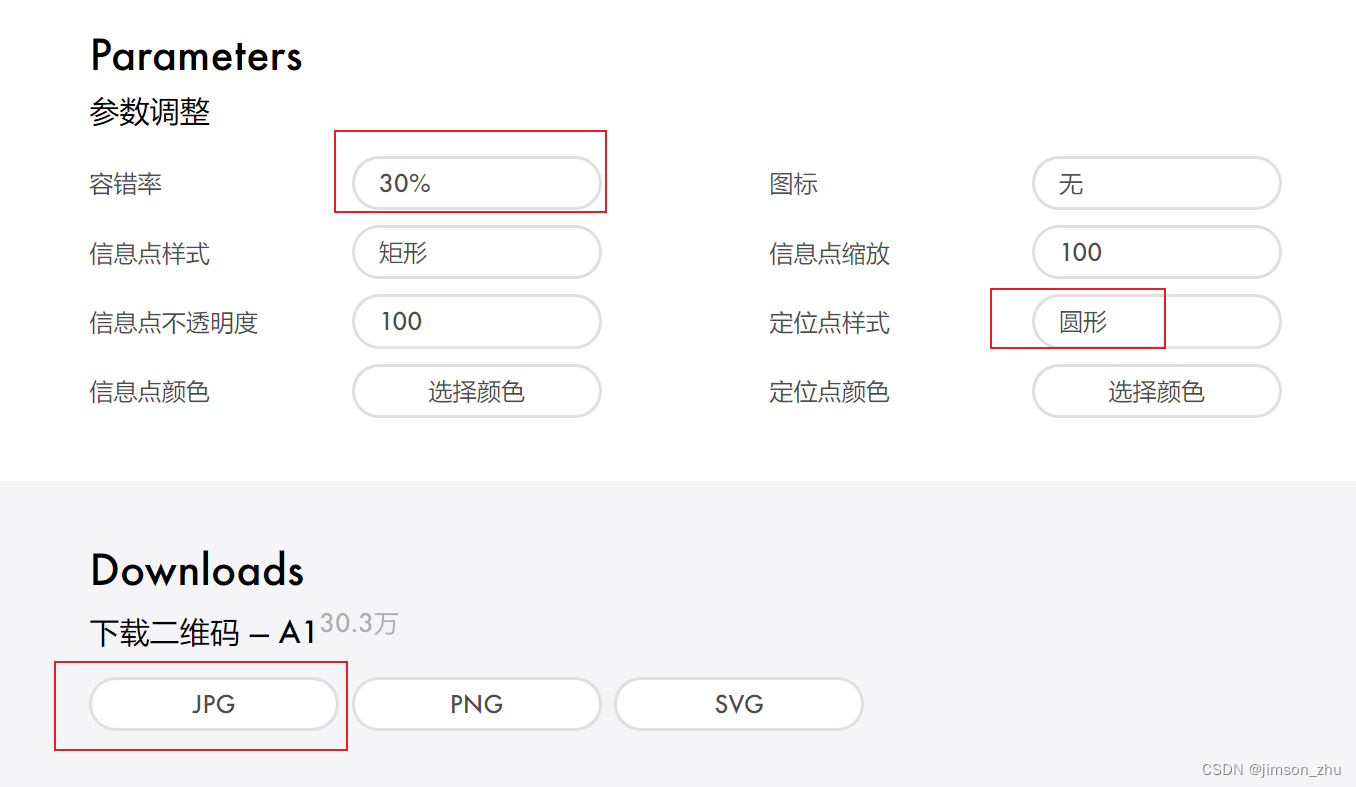
十八)Stable Diffusion使用教程:艺术二维码案例
今天说说怎么样使用SD生成艺术二维码。 我们直接上图。 方式有三种,分别如下: 1)方式一:直接 contronet 的tile模型进行控制 使用QRBTF Classic生成你的二维码。 首先输入网址,选择喜欢的二维码样式(推荐第一种就行): 然后选择相应参数,这里推荐最大的容错率,定…...

【LeetCode每日一题】53. 最大子数组和
https://leetcode.cn/problems/maximum-subarray/description/ 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 方式一:暴力…...

机器学习笔记 什么是协方差矩阵?
一、协方差矩阵 协方差矩阵是一种矩阵,用于表示随机向量中给定的元素对之间的协方差值。协方差矩阵也可以称为色散矩阵或方差-协方差矩阵。这是因为每个元素的方差是沿着矩阵的主对角线表示的。 协方差矩阵始终是方阵。此外,它是半正定且对称的。该矩阵在随机建模和主成分分析…...
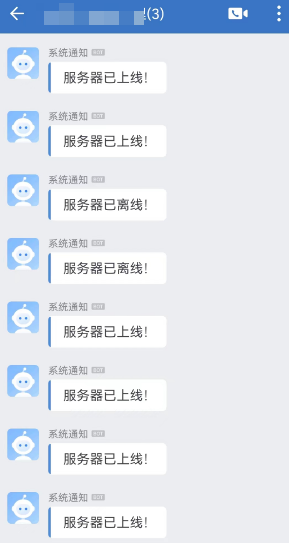
使用Python监控服务器在线状态
前言 在公司内网有一台服务器,有动态的公网IP,使用DDNS对外提供服务,但是会因为停电、服务器卡死等原因导致服务器离线。服务器离线后无法及时获知,因此需要实现在服务器离线的时候能够发送消息到手机上。 思路梳理 公司办理的…...
【JAVA】黑马MybatisPlus 学习笔记【二】【核心功能】
2.核心功能 刚才的案例中都是以id为条件的简单CRUD,一些复杂条件的SQL语句就要用到一些更高级的功能了。 2.1.条件构造器 除了新增以外,修改、删除、查询的SQL语句都需要指定where条件。因此BaseMapper中提供的相关方法除了以id作为where条件以外&…...
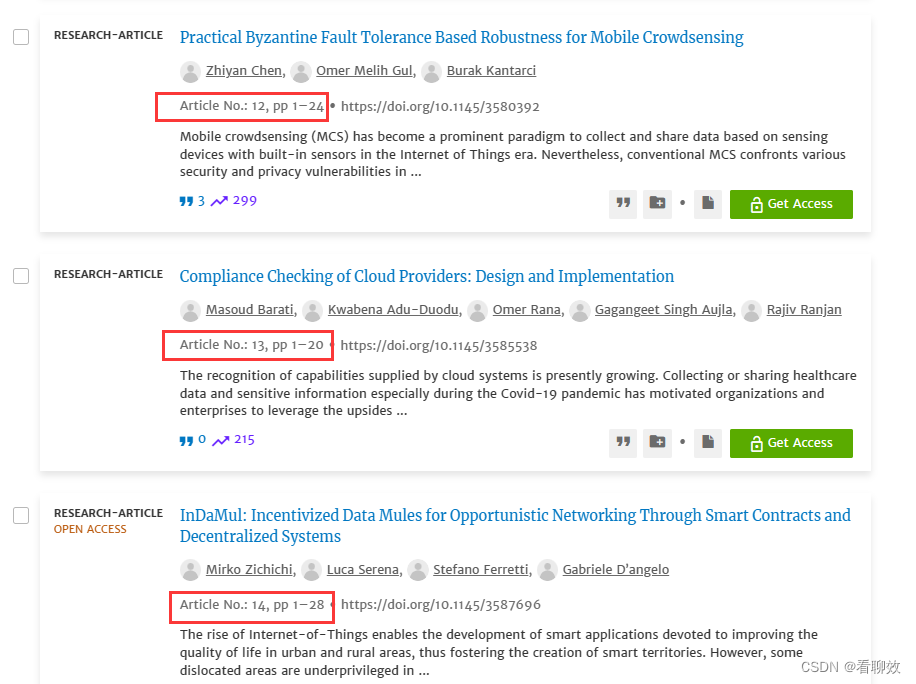
区块链实验室(30) - 区块链期刊:Distributed Ledger Technologies: Research and Practice
区块链涉及多学科及技术,众多期刊接收区块链文章。Distributed Ledger Technologies: Research and Practice是ACM出版集团的一本期刊。 Distributed Ledger Technologies: Research and Practice创刊历史很短,始于2022年,出版期数也不多。 载…...

Nginx【通俗易懂】《中篇》
目录 1.Url重写rewrite 2.防盗链 3.静态资源压缩 4.跨域问题 1.Url重写rewrite 🤩🤩🤩 1.1.rewrite书写格式 rewrite是实现URL重写的关键指令,根据regex(正则表达式)部分内容,重定向到rep…...

组件的二次封装
在React中,使用扩展运算符(...)来传递props的作用是将一个对象的所有可枚举属性(包括自身的和继承的)复制到新创建的对象中。当我们在二次封装组件时使用它,可以方便地将所有传递给我们的props传递给基础组…...
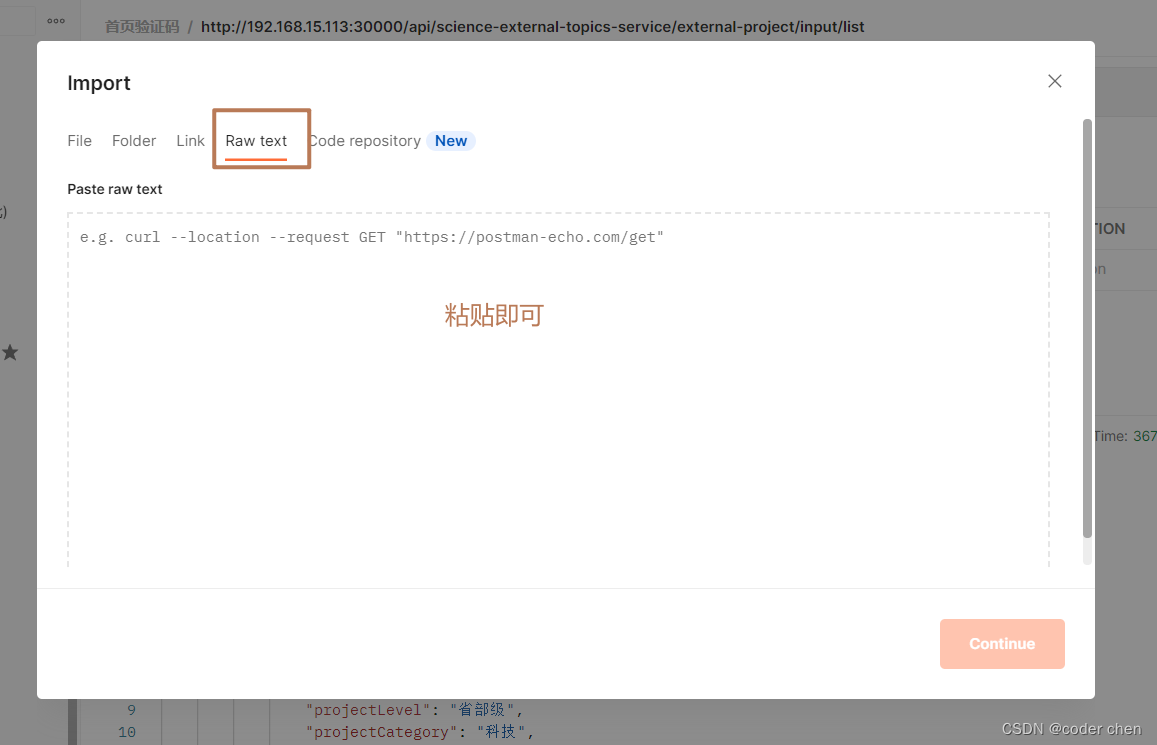
curl+postman 在java开发中的使用(提高效率)
概念 curl 是一个常用的命令行工具,用于发送各种类型的 HTTP 请求,包括 GET、POST、PUT、DELETE 等。它也可以用来下载文件、上传文件、设置 cookie、发送 multipart/form-data 等等。 使用 调用post接口 实际中的接口: curl --location…...
【电子取证:FTK IMAGER 篇】DD、E01系统镜像动态仿真
文章目录 【电子取证:FTK Imager 篇】DD、E01系统镜像动态仿真一、DD、E01系统镜像动态仿真 (一)使用到的软件 1、FTK Imager (v4.5.0.3)2、VMware Workstation 15 Pro (v15.5.2)(二)FTK Imager 挂载镜像 1、选择 …...

netcat瑞士军刀
netcat瑞士军刀 1、nc简介3、从示例中学习2、命令格式及常用参数 1、nc简介 nc(netcat)是一个短小精悍、功能实用、简单可靠的网络工具,主要有如下作用: (1)端口侦听,nc 可以作为 server 以 TC…...

【征稿倒计时十天】第三届高性能计算与通信工程国际学术会议(HPCCE 2023)
【有ISSN、ISBN号!!往届均已完成EI检索】 第三届高性能计算与通信工程国际学术会议(HPCCE 2023) 2023 3rd International Conference on High Performance Computing and Communication Engineering (HPCCE 2023) 2023年12月22-24日 | 中国哈尔滨 第三…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
