PyTorch实现逻辑回归
最终效果
先看下最终效果:
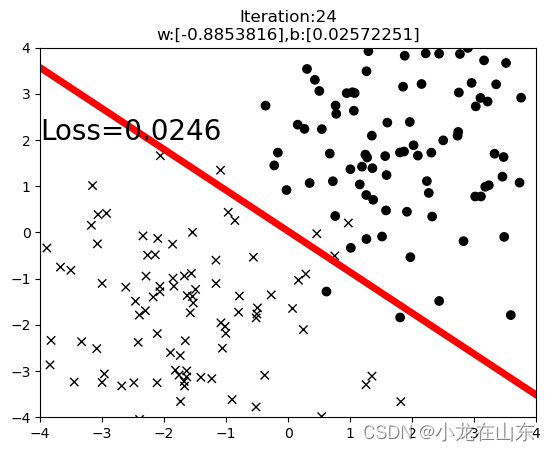
这里用一条直线把二维平面上不同的点分开。
生成随机数据
#创建训练数据
x = torch.rand(10,1)*10 #shape(10,1)
y = 2*x + (5 + torch.randn(10,1))#构建线性回归参数
w = torch.randn((1))#随机初始化w,要用到自动梯度求导
b = torch.zeros((1))#使用0初始化b,要用到自动梯度求导n_data = torch.ones(100, 2)
xy0 = torch.normal(2 * n_data, 1.5) # 生成均值为2.标准差为1.5的随机数组成的矩阵
c0 = torch.zeros(100)
xy1 = torch.normal(-2 * n_data, 1.5) # 生成均值为-2.标准差为1.5的随机数组成的矩阵
c1 = torch.ones(100)x,y = torch.cat((xy0,xy1),0).type(torch.FloatTensor).split(1, dim=1)
x = x.squeeze()
y = y.squeeze()
c = torch.cat((c0,c1),0).type(torch.FloatTensor)数据可视化
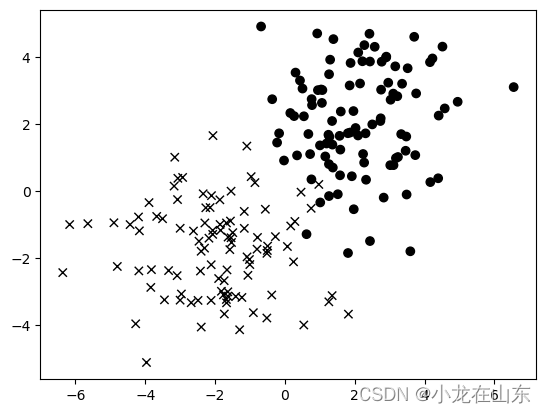
def plot(x, y, c):ax = plt.gca()sc = ax.scatter(x, y, color='black')paths = []for i in range(len(x)):if c[i].item() == 0:marker_obj = mmarkers.MarkerStyle('o')else:marker_obj = mmarkers.MarkerStyle('x')path = marker_obj.get_path().transformed(marker_obj.get_transform())paths.append(path)sc.set_paths(paths)return sc
plot(x, y, c)
plt.show()
使用x和o来表示两种不同类别的数据。
定义模型和损失函数
#构建逻辑回归参数
w = torch.tensor([1.,],requires_grad=True) # 随机初始化w
b = torch.zeros((1),requires_grad=True) # 使用0初始化bwx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b
loss = (0.5*(y-y_pred)**2).mean()这里使用了平方损失函数来估算模型准确度。
训练模型
最多训练100次,每次都会更新模型参数,当损失值小于0.03时停止训练。
xx = torch.arange(-4, 5)
lr = 0.02 #学习率
for iteration in range(100):#前向传播loss = ((torch.sigmoid(x*w+b-y) - c)**2).mean()#反向传播loss.backward()#更新参数b.data.sub_(lr*b.grad) # b = b - lr*b.gradw.data.sub_(lr*w.grad) # w = w - lr*w.grad#绘图if iteration % 3 == 0:plot(x, y, c)yy = w*xx + bplt.plot(xx.data.numpy(),yy.data.numpy(),'r-',lw=5)plt.text(-4,2,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'black'})plt.xlim(-4,4)plt.ylim(-4,4)plt.title("Iteration:{}\nw:{},b:{}".format(iteration,w.data.numpy(),b.data.numpy()))plt.show()if loss.data.numpy() < 0.03: # 停止条件break
全部代码
import torch
import matplotlib.pyplot as plt
import matplotlib.markers as mmarkers#创建训练数据
x = torch.rand(10,1)*10 #shape(10,1)
y = 2*x + (5 + torch.randn(10,1))#构建线性回归参数
w = torch.randn((1))#随机初始化w,要用到自动梯度求导
b = torch.zeros((1))#使用0初始化b,要用到自动梯度求导wx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + bn_data = torch.ones(100, 2)
xy0 = torch.normal(2 * n_data, 1.5) # 生成均值为2.标准差为1.5的随机数组成的矩阵
c0 = torch.zeros(100)
xy1 = torch.normal(-2 * n_data, 1.5) # 生成均值为-2.标准差为1.5的随机数组成的矩阵
c1 = torch.ones(100)x,y = torch.cat((xy0,xy1),0).type(torch.FloatTensor).split(1, dim=1)
x = x.squeeze()
y = y.squeeze()
c = torch.cat((c0,c1),0).type(torch.FloatTensor)def plot(x, y, c):ax = plt.gca()sc = ax.scatter(x, y, color='black')paths = []for i in range(len(x)):if c[i].item() == 0:marker_obj = mmarkers.MarkerStyle('o')else:marker_obj = mmarkers.MarkerStyle('x')path = marker_obj.get_path().transformed(marker_obj.get_transform())paths.append(path)sc.set_paths(paths)return sc
plot(x, y, c)
plt.show()#构建逻辑回归参数
w = torch.tensor([1.,],requires_grad=True)#随机初始化w
b = torch.zeros((1),requires_grad=True)#使用0初始化bwx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b
loss = (0.5*(y-y_pred)**2).mean()xx = torch.arange(-4, 5)
lr = 0.02 #学习率
for iteration in range(100):#前向传播loss = ((torch.sigmoid(x*w+b-y) - c)**2).mean()#反向传播loss.backward()#更新参数b.data.sub_(lr*b.grad) # b = b - lr*b.gradw.data.sub_(lr*w.grad) # w = w - lr*w.grad#绘图if iteration % 3 == 0:plot(x, y, c)yy = w*xx + bplt.plot(xx.data.numpy(),yy.data.numpy(),'r-',lw=5)plt.text(-4,2,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'black'})plt.xlim(-4,4)plt.ylim(-4,4)plt.title("Iteration:{}\nw:{},b:{}".format(iteration,w.data.numpy(),b.data.numpy()))plt.show()if loss.data.numpy() < 0.03:#停止条件break
相关文章:

PyTorch实现逻辑回归
最终效果 先看下最终效果: 这里用一条直线把二维平面上不同的点分开。 生成随机数据 #创建训练数据 x torch.rand(10,1)*10 #shape(10,1) y 2*x (5 torch.randn(10,1))#构建线性回归参数 w torch.randn((1))#随机初始化w,要用到自动梯度求导 b …...

什么是FPGA原型验证?
EDA工具的使用主要分为设计、验证和制造三大类。验证工作贯穿整个芯片设计流程,可以说芯片的验证阶段占据了整个芯片开发的大部分时间。从芯片需求定义、功能设计开发到物理实现制造,每个环节都需要进行大量的验证。 现如今验证方法也越来越多ÿ…...

基于VUE3+Layui从头搭建通用后台管理系统(前端篇)十四:系统设置模块相关功能实现
一、本章内容 本章使用已实现的公共组件实现系统管理中的系统设置模块相关功能,包括菜单管理、角色管理、日志管理、用户管理、系统配置、数据字典等。 1. 详细课程地址: 待发布 2. 源码下载地址: 待发布 二、界面预览 三、开发视频 3.1 B站视频地址:...
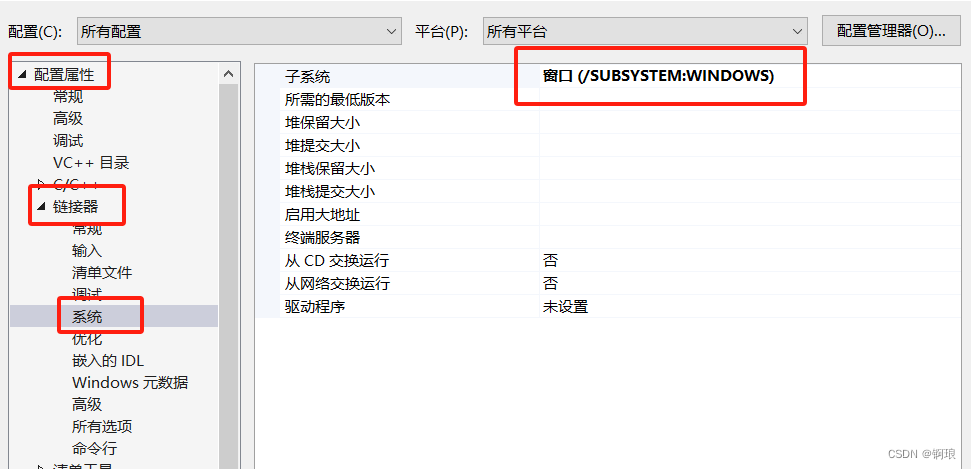
使用Visual Studio(VS)创建空项目的Win32桌面应用程序【main函数入口变WinMain】
前言 在Visual Studio中直接新建Windows桌面应用程序会有很多多余的代码生成,本文将提供从空项目创建Win32项目的方法,解决新建空项目直接使用WinMain代码编译报错的问题 例如:LNK2019 :无法解析的外部符号 参考博客࿱…...
基于自动化脚本批量上传依赖到nexus内网私服
前言 因为某些原因某些企业希望私服是不能连接外网的,所以需要某些开源依赖需要我们手动导入到nexus中,尽管nexus为我们提供了web页面。但是一个个手动导入显然是一个庞大的工程。 对此我们就不妨基于脚本的方式实现这一过程。 预期效果 笔者本地仓库…...

Linux中ps命令使用指南
目录 1 前言2 ps命令的含义和作用3 ps命令的基本使用4 常用选项参数5 一些常用情景5.1 查看系统中的所有进程(标准语法)5.2 使用 BSD 语法查看系统中的所有进程5.3 打印进程树5.4 获取线程信息5.5 获取安全信息5.6 查看以 root 用户身份(实际…...

PHP开发语言中,网页端常用的标签
在PHP开发语言中,网页端常用的标签包括以下几种: <html>:用于定义整个HTML文档。<head>:用于定义文档的头部,包含元数据、样式表和脚本等。<title>:用于定义文档的标题,显示…...
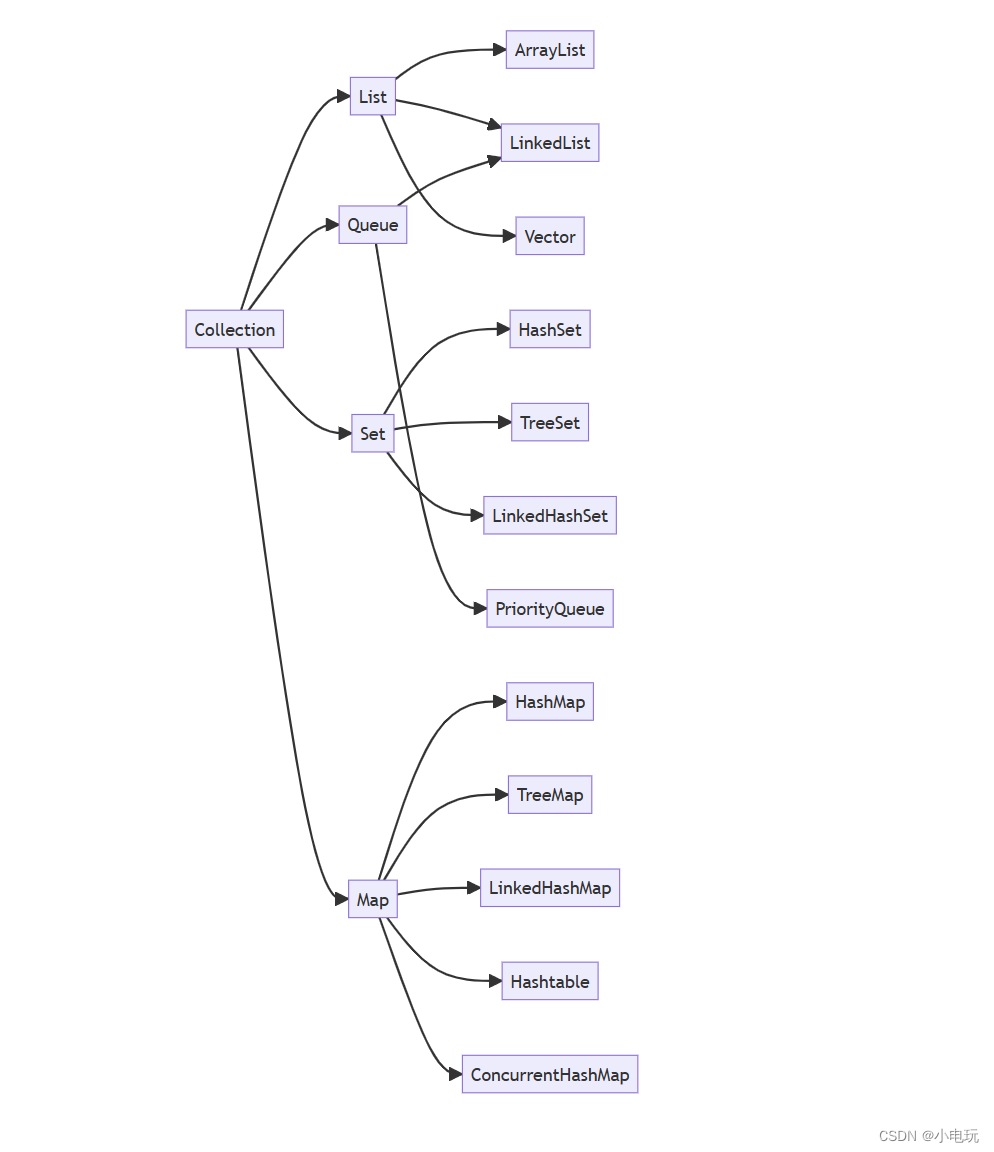
Java 入门第四篇 集合
Java 入门第四篇 集合 一,什么是集合 在Java中,集合(Collection)是一种用于存储和操作一组对象的容器类。它提供了一系列的方法和功能,用于方便地管理和操作对象的集合。集合框架是Java中非常重要和常用的一部分&…...

VBA技术资料MF93:将多个Excel表插入PowerPoint不同位置
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...

STM32 MCU的易坑点收集
IIC配置中的Clock No Stretch Mode Clock Stretch Mode时钟延长模式: 时钟延长是一个术语,某些从设备可以把时钟线拉低,主设备发现自己释放时钟线之后时钟线还没有变成高电平,就会停止发送数据,然后等待从设备释放时钟…...

Vue3项目filter.js组件封装
1、element-plus(el-table)修改table的行样式 export function elTableRowClassName({ row, rowIndex }) {if (rowIndex % 2 ! 0) {return default-row} }2、时间戳转换格式 export function parseTimeFilter(dateTime, dateType) {if (dateTime || dateTime undefined ||…...

Linux: pwd命令查看当前工作目录
pwd 是 Linux 和其他类 Unix 操作系统中的一个命令,用于显示当前工作目录的绝对路径。 语法 pwd 描述 pwd 是 "print working directory" 的缩写,它用于打印当前工作目录的完整路径。这对于确定当前目录位置非常有用,特别是在嵌…...

【深度学习】PHP操作mysql数据库总结
一.PHP数据库的扩展分类 1.MySQL 扩展是针对 MySQL 4.1.3 或更早版本设计的,是 PHP 与 MySQL数据库交互的早期扩展。由于其不支持 MySQL 数据库服务器的新特性,且安全性差,在项目开发中不建议使用,可用 MySQLi 扩展代替。 2.MySQ…...

【送书活动】探究AIGC、AGI、GPT和人工智能大模型
文章目录 前言01 《ChatGPT 驱动软件开发》推荐语 02 《ChatGPT原理与实战》推荐语 03 《神经网络与深度学习》推荐语 04 《AIGC重塑教育》推荐语 05 《通用人工智能》推荐语 后记赠书活动 前言 人工智能技术在过去几年中发展迅猛,得益于大数据、云计算、深度学习等…...
Apple Find My「查找」认证芯片找哪家,认准伦茨科技ST17H6x芯片
深圳市伦茨科技有限公司(以下简称“伦茨科技”)发布ST17H6x Soc平台。成为继Nordic之后全球第二家取得Apple Find My「查找」认证的芯片厂家,该平台提供可通过Apple Find My认证的Apple查找(Find My)功能集成解决方案。…...
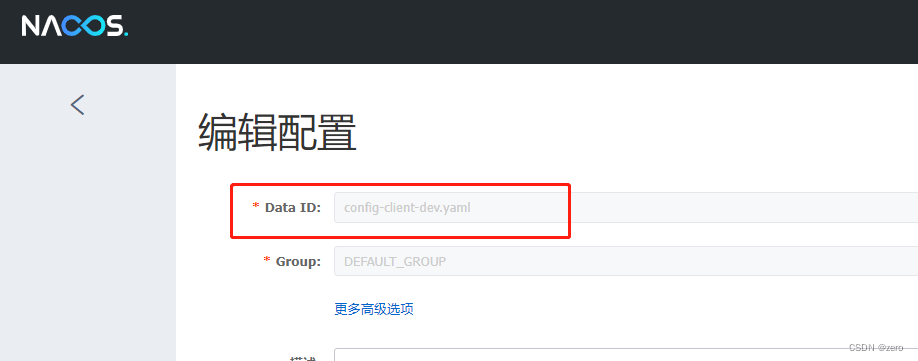
java.lang.IllegalArgumentException: Could not resolve placeholder XXX‘ in value
问题描述 使用Springcloudalibaba的nacos作为配置中心,服务启动时报错: java.lang.IllegalArgumentException: Could not resolve placeholder XXX‘ in value java.lang.IllegalArgumentException: Param ‘serviceName’ is illegal, serviceName is …...

自动机器学习是什么?概念及应用
自动机器学习 (Auto Machine Learning) 的应用和方法 随着众多企业在大量场景中开始采用机器学习,前后期处理和优化的数据量及规模指数级增长。企业很难雇用充足的人手来完成与高级机器学习模型相关的所有工作,因此机器学习自动化工具是未来人工智能 (A…...

el-date-picker限制选择7天内禁止内框选择
需求:elementPlus时间段选择框需要满足:①最多选7天时间。②不能手动输入。 <el-date-picker v-model"timeArrange" focus"timeEditable" :editable"false" type"datetimerange" range-separator"至&qu…...
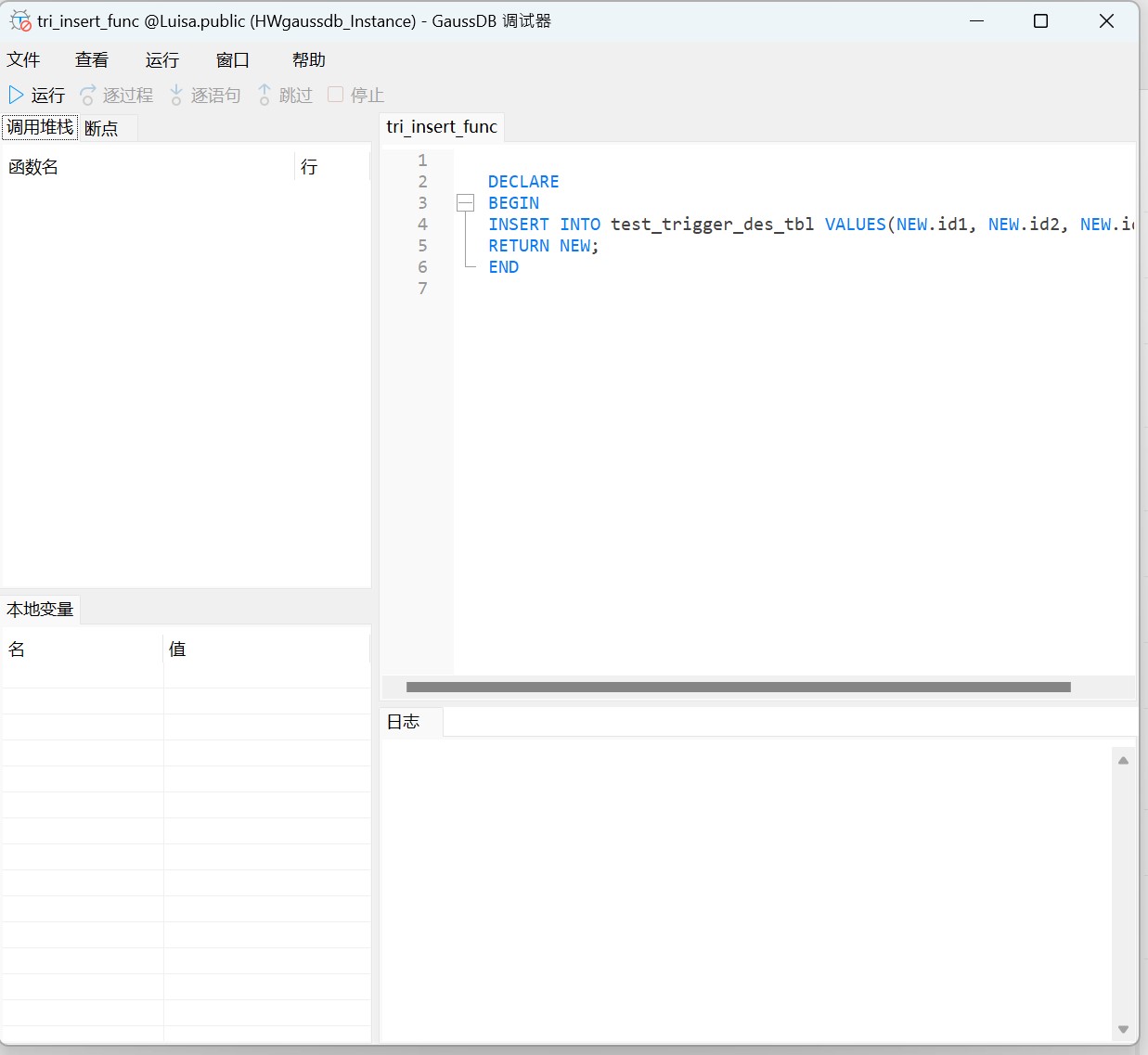
Navicat 技术指引 | 适用于 GaussDB 分布式的调试器
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…...

人工智能导论习题集(3)
第五章:不确定性推理 题1题2题3题4题5题6题7题8 题1 题2 题3 题4 题5 题6 题7 题8...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
