leetcode 二数之和 三数之和 四数之和
leetcode 二数之和 三数之和 四数之和
又到了不想写博客的环节,不想归不想,有些事情还是要做的,今天总结的是多数之和的问题。
二数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
思考:对于这道题其实很简单,不过要想到利用哈希法来做可能有点难度,一来对哈希结构相关的语法不熟悉,而来贪图方便,就用两个for循环解决了,这里需要注意的是两个for循环的起始位置,需要遍历到所有的可能性。
法一:
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {for(int i=0;i<nums.size()-1;i++){for(int j=i+1;j<nums.size();j++){if(nums[i]+nums[j]==target){return {i,j};}}}return {};}
};
法二:
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int,int> umap;for(int i=0;i<nums.size();i++){auto iter=umap.find(target-nums[i]);if(iter!=umap.end()){return {iter->second,i};}else{umap.insert(pair<int,int>(nums[i],i));}}return {};}
};
三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
思考:这道题按照正常的思路也可以,不过剪枝和去重的时候比较麻烦,容易少写或者多写,所以最好按照双指针的写法来写
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(),nums.end());for(int i=0;i<nums.size();i++){if(nums[i]>0){break;}if(i>0&&nums[i]==nums[i-1]){continue;}int left=i+1;int right=nums.size()-1;while(right>left){if(nums[i]+nums[left]+nums[right]>0) right--;else if(nums[i]+nums[left]+nums[right]<0) left++;else{result.push_back({nums[i],nums[left],nums[right]});while(right>left&&nums[right]==nums[right-1]) right--;while(right>left&&nums[left]==nums[left+1]) left++;right--;left++;}}}return result;}
};
四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
思考:这道题和三数之和的解法很像,也是双指针,这样去重时不容易出错,但是有个注意的点就是在判断第二个数时需要参照第一个数的写法
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> result;sort(nums.begin(),nums.end());for(int i=0;i<nums.size();i++){if(nums[i]>target&&nums[i]>=0){break;}if(i>0&&nums[i]==nums[i-1]){continue;}for(int j=i+1;j<nums.size();j++){if(nums[i]+nums[j]>target&&nums[i]+nums[j]>=0){break;}if(j>i+1&&nums[j]==nums[j-1]){continue;}int left=j+1;int right=nums.size()-1;while(right>left){if((long)nums[i]+nums[j]+nums[left]+nums[right]>target) right--;else if((long)nums[i]+nums[j]+nums[left]+nums[right]<target) left++;else{result.push_back(vector<int>{nums[i],nums[j],nums[left],nums[right]});while(right>left&&nums[right]==nums[right-1]) right--;while(right>left&&nums[left]==nums[left+1]) left++; left++;right--;}}}}return result;}
};
相关文章:

leetcode 二数之和 三数之和 四数之和
leetcode 二数之和 三数之和 四数之和 又到了不想写博客的环节,不想归不想,有些事情还是要做的,今天总结的是多数之和的问题。 二数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target …...

制衣厂生产ERP系统怎么样?制衣厂生产ERP软件哪个好
有很多的制衣厂在订单处理、物料、仓储、销售、仓储、物料编码、车间成本核算、计件工资核算等方面还存在不少改进空间。 而经过多年的发展,现如今制衣行业的竞争比较激烈,如何提升各业务部门协同效率,减少车间物料损耗,简化生产…...
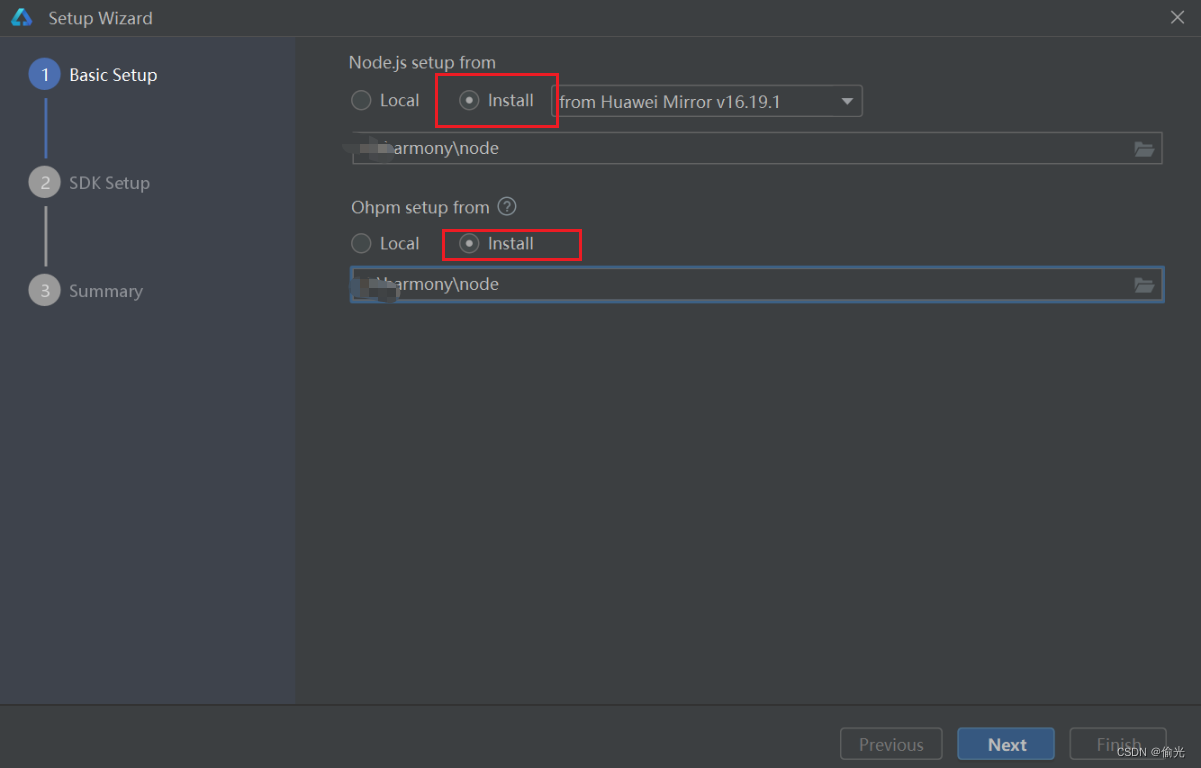
安装 DevEco Studio 后不能用本地 Node.js 打开
安装 DevEco Studio 后第一次打开时,不能用本地 Node.js 打开 答:因为本地 Node.js 文件夹名字中有空格 Node.js路径只能包含字母、数字、“。”、“_”、“-”、“:”和“V” 解决方法: 1.修改文件夹名称 2.重新下载 注意:找一…...
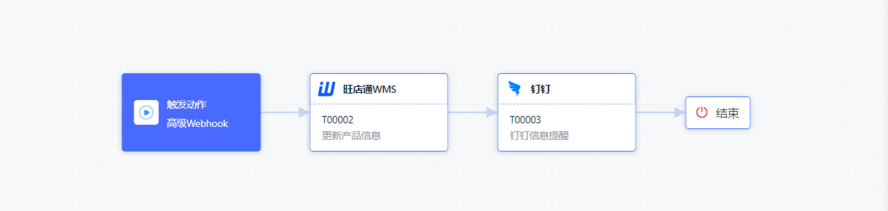
AppLink+WMS,实现仓储管理一体化
WMS像全能的库管员,可以在线还原真实仓库,让企业进行科学化、条理化、俯视化的仓库管理。 随着移动互联网和物流行业的快速发展,如何提高仓储管理的效率和准确性成为了企业关注的焦点。在这个背景下,结合AppLink和WMS系统&#x…...

如果是你,你选SOHO还是跟单?
昨天看到有人在讨论外贸跟单和外贸业务,谁的压力更大的问题?她们讨论的这个问题,源于一个年近四十准备二胎的宝妈,她做跟单十来年了,最近失业迷茫中,在纠结是否要SOHO?作为一个在工贸一体工厂做…...

大语言模型--能力
能力 大语言模型 能力从语言模型到任务模型的转化语言建模总结 从语言模型到任务模型的转化 在自然语言处理的世界中,语言模型 p p p是一种对代币序列 x 1 : L x_{1:L} x1:L这样的模型能够用于评估序列,例如 p ( t h e , m o u s e , a t e , t h e ,…...

安装LLaMA-Factory微调chatglm3,修改自我认知
安装git clone https://github.com/hiyouga/LLaMA-Factory.git conda create -n llama_factory python3.10 conda activate llama_factory cd LLaMA-Factory pip install -r requirements.txt 之后运行 单卡训练, CUDA_VISIBLE_DEVICES0 python src/train_web.py…...
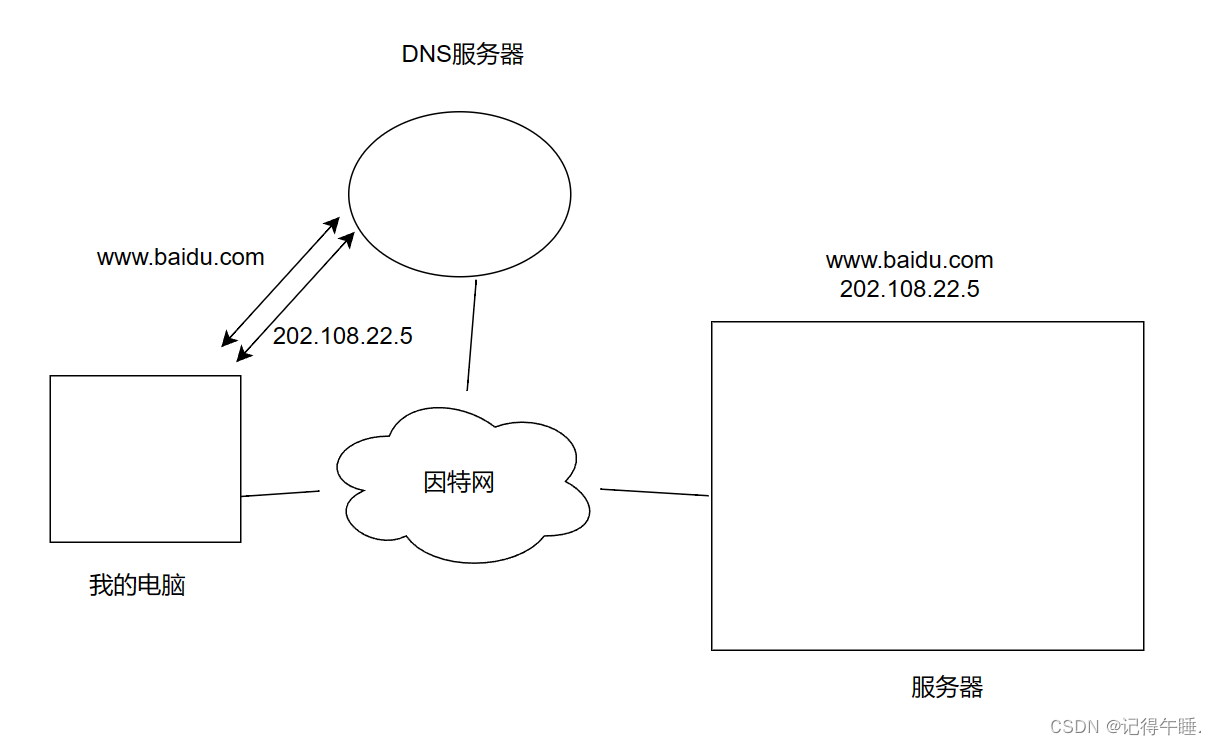
以太网协议与DNS
以太网协议 以太网协议DNS 以太网协议 以太网用于在计算机和其他网络设备之间传输数据,以太网既包含了数据链路层的内容,也包含了物理层的内容. 以太网数据报: 其中目的IP和源IP不是网络层的目的IP和源IP,而是mac地址.网络层的主要负责是整体的转发过程,数据链路层负责的是局…...

Spring Boot的日志
打印日志 打印日志的步骤: • 在程序中得到日志对象. • 使用日志对象输出要打印的内容 在程序中得到日志对象 在程序中获取日志对象需要使用日志工厂LoggerFactory,代码如下: package com.example.demo;import org.slf4j.Logger; import org.slf4j.LoggerFactory;public c…...
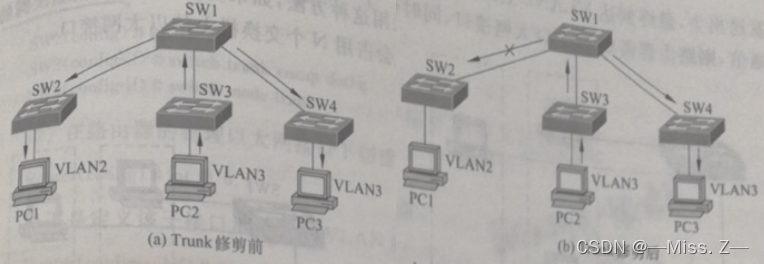
Cisco Packet Tracer配置命令——交换机篇
交换机VLAN配置 在简单的网络环境中,当交换机配置完端口后,即可直接应用,但若在复杂或规模较大的网络环境中,一般还要进行VLAN的规划,因此在交换机上还需进行 VLAN 的配置。交换机的VLAN配置工作主要有VLAN的建立与删…...

python单例模式
设计模式:单例模式(Singleton Pattern)。单例模式确保一个类只有一个实例,并提供一个全局访问点来获取这个实例。 class Singleton:_instance Nonedef __new__(cls):if cls._instance is None:cls._instance super().__new__(cl…...

环境保护:人类生存的最后机会
随着科技的进步和人类文明的不断发展,地球上的自然资源也在以惊人的速度消耗殆尽。人类对于环境的无止境的掠夺,使得我们的地球正面临着前所未有的环境危机。环境污染、全球变暖、大规模灭绝等问题不断困扰着我们,似乎指向了人类生存的最后机…...
头歌-Python 基础
第1关:建模与仿真 1、 建模过程,通常也称为数学优化建模(Mathematical Optimization Modeling),不同之处在于它可以确定特定场景的特定的、最优化或最佳的结果。这被称为诊断一个结果,因此命名为▁▁▁。 填空1答案:决…...
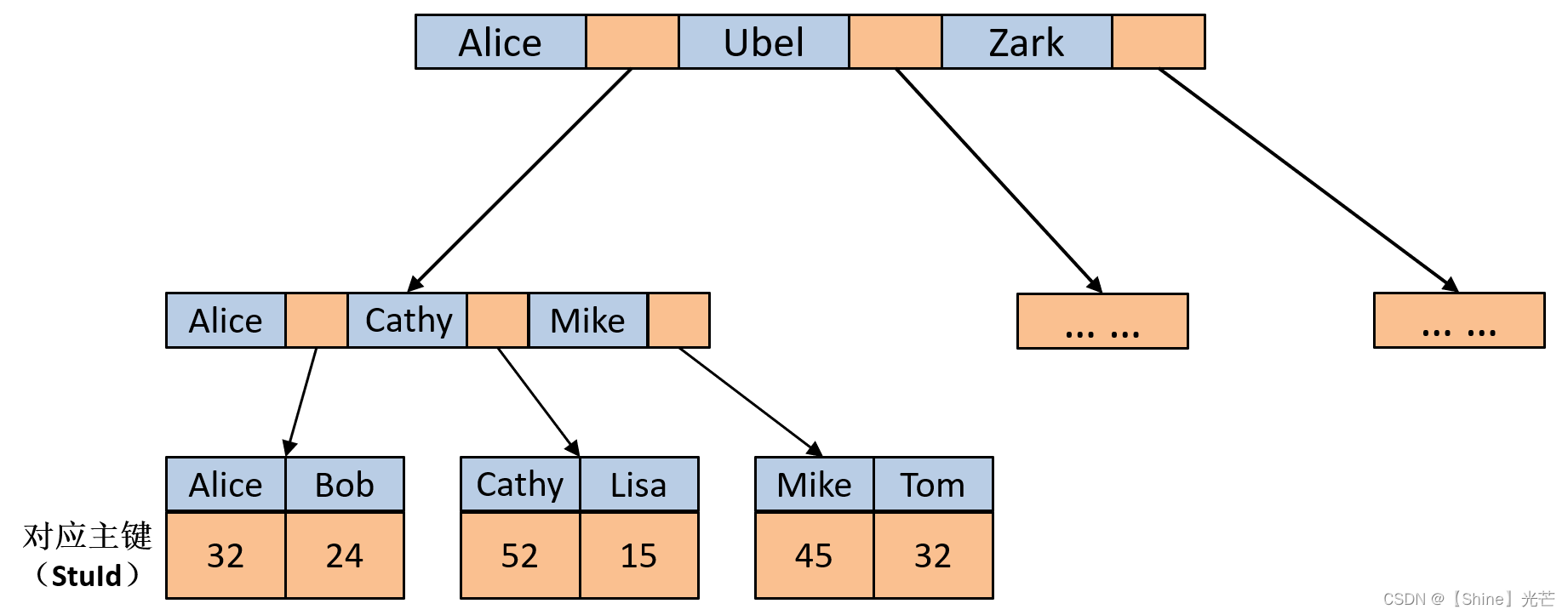
C++数据结构:B树
目录 一. 常见的搜索结构 二. B树的概念 三. B树节点的插入和遍历 3.1 插入B树节点 3.2 B树遍历 四. B树和B*树 4.1 B树 4.2 B*树 五. B树索引原理 5.1 索引概述 5.2 MyISAM 5.3 InnoDB 六. 总结 一. 常见的搜索结构 表示1为在实际软件开发项目中,常用…...

【07】ES6:对象的扩展
一、对象字面量语法扩展 1、属性简写 当属性名称和属性值的变量名称相同时,可以省略冒号的变量名称。 const foo barconst baz { foo } // 等同于 const baz { foo: foo }baz // { foo: bar }function f(x, y) {return { x, y } } // 等同于 function f(x, y)…...
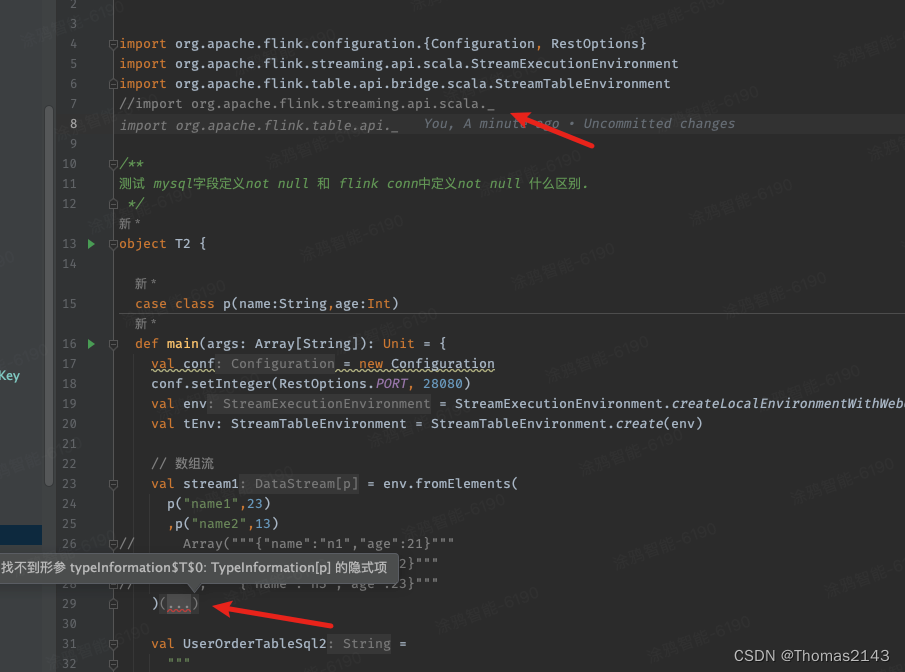
flink找不到隐式项
增加 import org.apache.flink.streaming.api.scala._ 即可...

【网络编程】-- 04 UDP
网络编程 6 UDP 6.1 初识Tomcat 服务端 自定义 STomcat S 客户端 自定义 C浏览器 B 6.2 UDP 6.2.1 udp实现发送消息 接收端: package com.duo.lesson03;import java.net.DatagramPacket; import java.net.DatagramSocket; import java.net.SocketExceptio…...

【脚本】图片-音视频-压缩文件处理
音视频处理 一,图片操作1,转换图片格式2,多张图片合成视频 二,音频操作1,转换音频格式2,分割音频为多段3,合成多段音频 三,视频操作1,转换视频格式2,提取视频…...

跨品牌的手机要怎样相互投屏?iPhone和iPad怎么相互投屏?
选择买不同品牌的手机是基于品牌声誉、产品特点、价格和性价比等多个因素的综合考虑。每个人的需求和偏好不同,选择适合自己的手机品牌是一个个人化的决策。 一些品牌可能更加注重摄影功能,而其他品牌可能更加注重性能和速度。选择不同品牌的手机可以根据…...
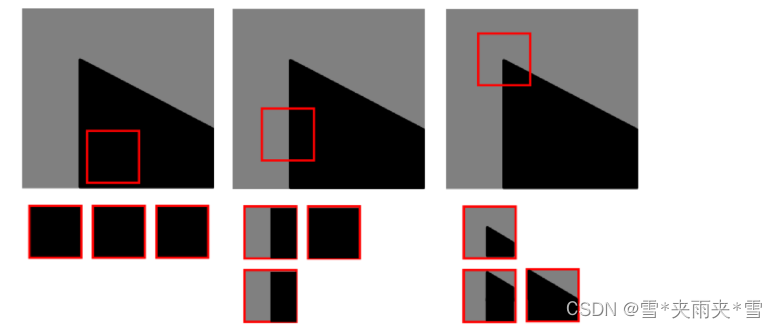
图像特征提取-角点
角点特征 大多数人都玩过拼图游戏。首先拿到完整图像的碎片,然后把这些碎片以正确的方式排列起来从而重建这幅图像。如果把拼图游戏的原理写成计算机程序,那计算机就也会玩拼图游戏了。 在拼图时,我们要寻找一些唯一的特征,这些…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
