弟弟的作业
问题 G: 弟弟的作业
[命题人 : 外部导入]
时间限制 : 1.000 sec 内存限制 : 128 MB
题目描述
你的弟弟刚做完了“100以内数的加减法”这部分的作业,请你帮他检查一下。每道题目(包括弟弟的答案)的格式为a+b=c或者a-b=c,其中a和b是作业中给出的,均为不超过100的非负整数;c是弟弟算出的答案,可能是不超过200的非负整数,也可能是单个字符"?",表示他不会算。
输入
输入文件包含不超过100行,以文件结束符结尾。每行包含一道题目,格式保证符合上述规定,且不包含任何空白字符。输入的所有整数均不含前导0。
输出
输出仅一行,包含一个非负整数,即弟弟答对的题目数量。
样例输入 Copy
1+2=3
3-1=5
6+7=?
99-0=99
样例输出 Copy
2
#include<stdio.h>
int main()
{int a=0, b=0,num=0,c,mm;char plusAndMinus=0,equal=0;while ((mm=scanf("%d %c%d%c%d", &a, &plusAndMinus, &b, &equal,&c))!=EOF){if (mm != 5){getchar();continue;}else if (plusAndMinus == '+'){if (a + b == c)num++;}else{if (c == '?');else if (a - b == c)num++;}}printf("%d", num);return 0;
}
利用scanf的返回值
相关文章:

弟弟的作业
问题 G: 弟弟的作业 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 你的弟弟刚做完了“100以内数的加减法”这部分的作业,请你帮他检查一下。每道题目(包括弟弟的答案)的格式为abc或者a-bc,其中a和b是作…...

代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字 中等 相关标签 相关企业 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10输出: …...

出现 java: 找不到符号 符号: 变量 log 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 增加编译参数3.2 增加lombok插件3.3 清楚本地缓存1. 问题所示 使用Springboot启动项目的时候,出现如下bug: java: 找不到符号符号: 变量 log位置: 类 org.springblade.example.consumer.rpc.BlogStu...
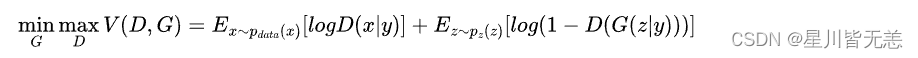
大数据机器学习与深度学习—— 生成对抗网络(GAN)
GAN概述 在讲GAN之前,先讲一个小趣事,你知道GAN是怎么被发明的吗?据Ian Goodfellow自己说: 之前他一直在研究生成模型,可能是一时兴起,有一天他在酒吧喝酒时,在酒吧里跟朋友讨论起生成模型。然…...

vue前端访问Django channels WebSocket失败
现象 前端报错:SSH.vue:51 WebSocket connection to ‘ws://127.0.0.1:8000/server/terminal/120.59.88.26/22/1/’ failed: 后端报错:Not Found: /server/terminal/120.79.83.26/22/1/ 原因 django的版本与channels的版本不匹配(django…...

厉害了!水浸监控技术有升级啦
水浸监控在今天的社会中变得愈发重要,特别是在各种行业和场所。面对突发的水灾,及时有效的监测和预警系统可以帮助组织减少损失,保障人员和财产的安全。 客户案例 商业办公楼 合肥某大型商业办公楼面临着水灾风险,而传统的监控系…...

【开题报告】基于SpringBoot的大学生心理教育平台的设计与实现
1.研究背景 大学生心理健康问题一直备受关注。随着社会压力的增加、人际关系的复杂化以及学业与就业压力等因素的影响,大学生心理健康问题日益突出。因此,设计并实现基于SpringBoot的大学生心理教育平台具有重要的研究意义和实践价值。 (1&…...
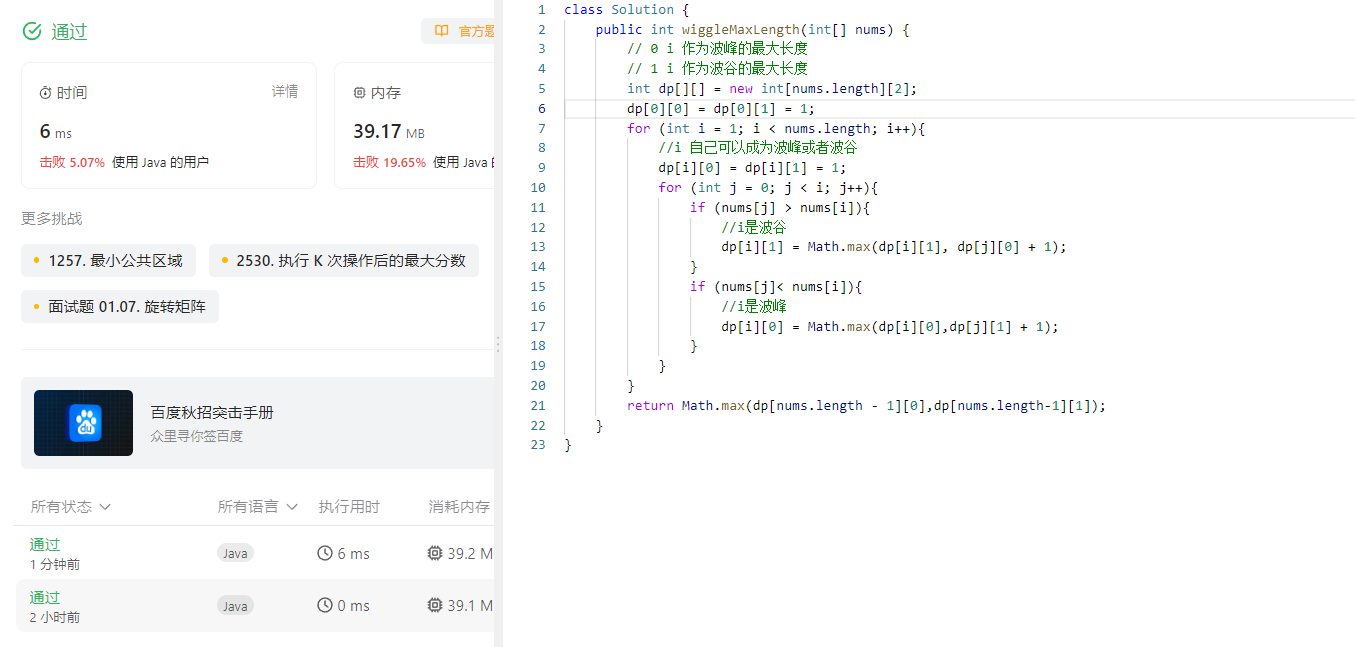
376. 摆动序列
376. 摆动序列 原题链接:完成情况:解题思路:参考代码:_376摆动序列_376摆动序列 错误经验吸取 原题链接: 376. 摆动序列 https://leetcode.cn/problems/wiggle-subsequence/description/ 完成情况: 解题…...

现在个人想上架微信小游戏已经这么难了吗...
引言 大家好,最近我突然想起来我还有一款微信小游戏还没有上架,于是捣鼓了一天把游戏完善了一下,然后准备提交审核,却发现异常的艰难... 1.为什么难? 相信大家都大概知道,自从微信平台宣布 9月1日起&…...
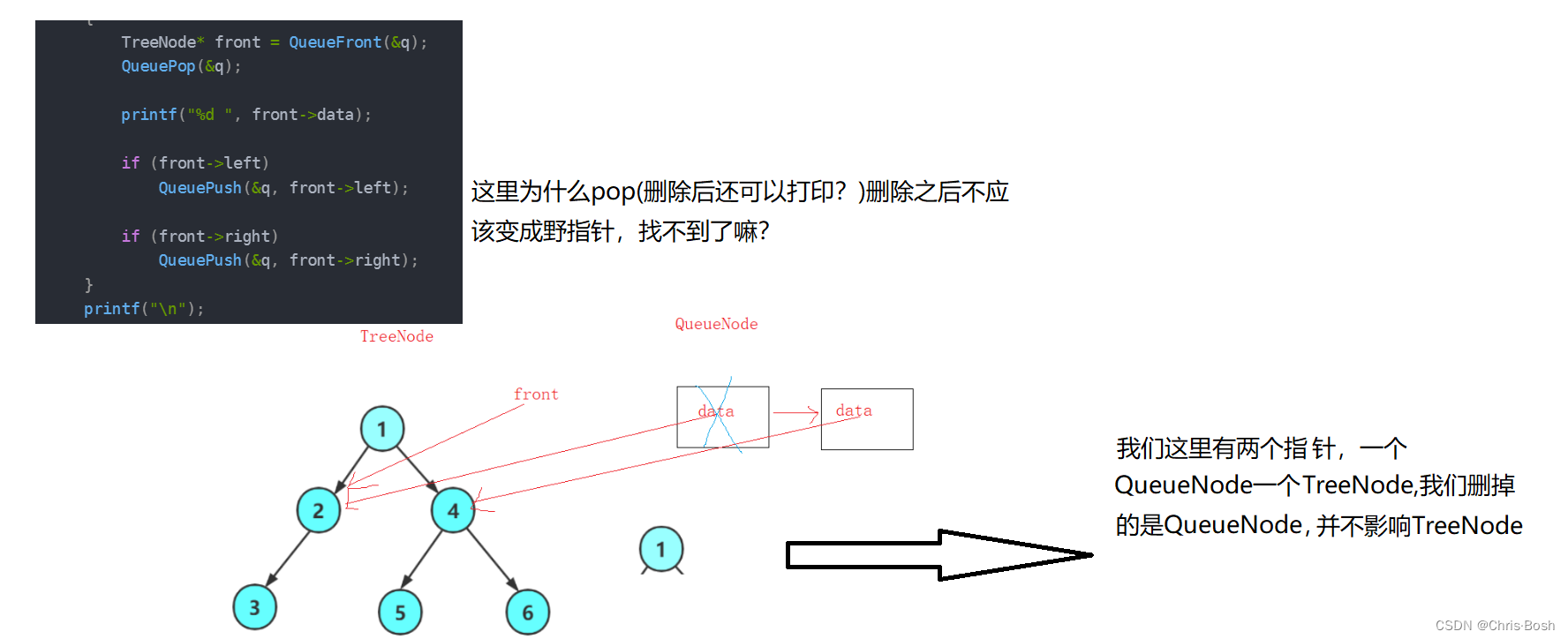
C语言数据结构-----二叉树(2)堆的深入理解及应用、链式二叉树的讲解及代码实现
前言 本篇文章讲述的内容有部分是上一节写过的。重复内容不会再进行说明,大家可以看上一节内容 链接: C语言数据结构-----二叉树(1)认识数、二叉树、堆及堆的代码实现 文章目录 前言1.使用堆解决TOP-K问题2.向下调整堆的时间复杂度与向上调整堆的时间复杂度对比3.堆…...

【算法】【动规】等差数列划分
跳转汇总链接 👉🔗算法题汇总链接 1.2 等差数列划分 🔗题目链接 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是…...
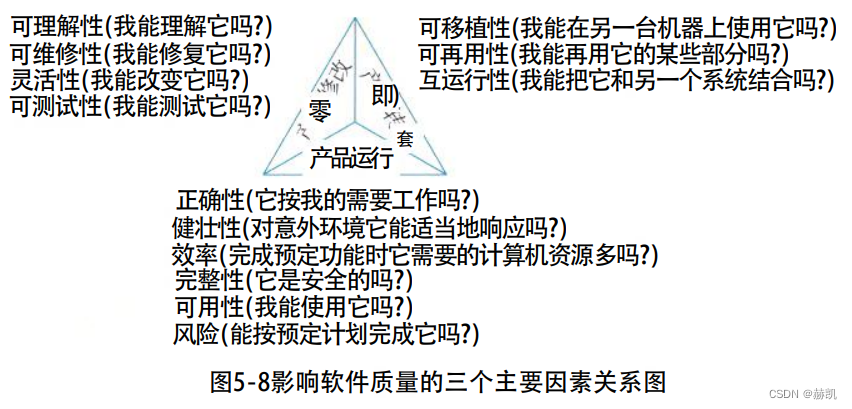
系统架构设计师教程(五)软件工程基础知识
软件工程基础知识 5.1 软件工程5.1.1 软件工程定义5.1.2 软件过程模型5.1.3 敏捷模型敏捷开发的特点敏捷方法的核心思想主要敏捷方法简介 5.1.4 统一过程模型 (RUP)RUP的生命周期RUP中的核心概念RUP的特点 5.1.5 软件能力成熟度模型 5.2 需求工程5.2.1 需求获取需求获取的基本步…...
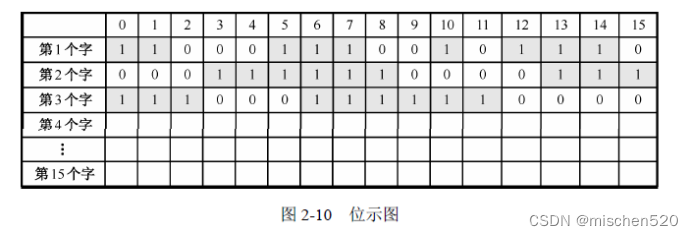
计算机中的文件管理
操作系统对计算机的管理包括两个方面:硬件资源和软件资源。硬件资源的管理包括CPU 的管理、存储器的管理、设备管理等,主要解决硬件资源的有效和合理利用问题。 软件资源包括各种系统程序、各种应用程序、各种用户程序,也包括大量的文档材料、…...

Linux常见排错思路及命令
Linux常见排错思路及命令 一、引言 在Linux系统中,由于其高度可配置和可定制的特性,可能会遇到各种问题。本文将介绍一些常见的排错思路,并提供一些常用的命令,以帮助您快速定位和解决问题。 二、常见排错思路 查看系统日志 …...

【springboot】【easyexcel】excel文件读取
目录 pom.xmlExcelVo逐行读取并处理全部读取并处理向ExcelListener 传参 pom.xml <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version> </dependency>ExcelVo 字段映射…...
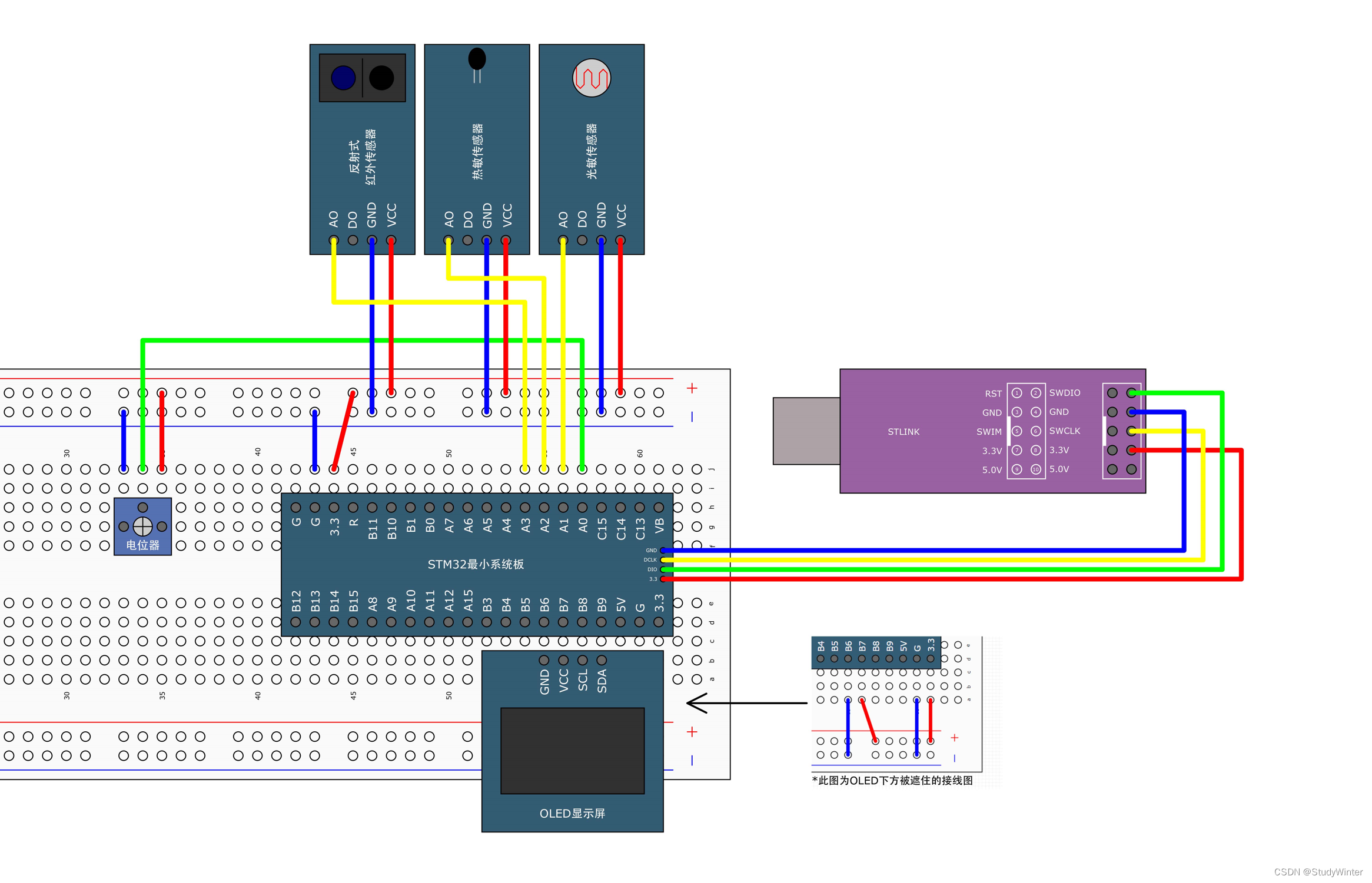
【STM32】ADC模数转换器
1 ADC简介 ADC(Analog-Digital Converter)模拟-数字转换器 ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 STM32是数字电路,只有高低电平,没有几V电压的概念ÿ…...

Git篇---第九篇
系列文章目录 文章目录 系列文章目录前言一、使用过git merge和git rebase吗?它们之间有什么区别?二、使用过git cherry-pick,有什么作用?前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看…...

Paper Reading: (ACRST) 基于自适应类再平衡自训练的半监督目标检测
目录 简介工作重点方法CropBankFBRAFFRTwo-stage Pseudo-label Filtering 实验与SOTA比较消融实验 简介 题目:《Semi-Supervised Object Detection with Adaptive Class-Rebalancing Self-Training》,AAAI’22, 基于自适应类再平衡自训练的半…...

2023年贺岁电影:一眼多,二眼好多
如果从11月末开始统计,今年贺岁档共有72部贺岁片,平均一天就有2部电影上映,看完总计需要花费7400分钟。 这个数量几乎快赶上2021年到2022年贺岁片的总和。 今年电影市场快速回暖以来,多部爆款作品接力上映,持续刺激市…...

软件测试面试中基础与功能的问题
一、 你们的测试流程是怎么样的? 答:1.项目开始阶段, BA (需求分析师) 从用户方收集需求并将需求转化为规格说明书,接 下来在 项目组领导 会组织需求评审。 2.需求评审通过后,BA 会组织 项目…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
