有趣的数学 数学建模入门三 数学建模入门示例两例 利用微积分求解
一、入门示例1
1、问题描述
某宾馆有150间客房,经过一段时间的经营,该宾馆经理得到一些数据:如果每间客房定价为200元,入住率为55%;定价为180元,入住率为65%;定价为160元,入住率为75%;定价为140元,入住率为85%。
经理想要使每天的收入最高,问每间客房的定价应为多少?
2、模型假设
假设1:每间客房的最高定价为200元。
假设2:根据题目提供的数据,可设随着房价的下降,入住率呈线性增长。
假设3:宾馆的每间客房的定价相等。
3、模型建立
设表示宾馆一天的总收入,与200元相比每间客房降低的房价为
元。由假设2可得,每降低1元房价,入住率就增加
。
因此,150间客房,最高房价200,1元入住率为0.005,可以如下公式:
由,可知
。于是问题转化为求当
时,总收入
的最大值是多少?
4、模型求解
我们整理一下上面的方程。
然后利用一元函数微分,令
可得当,即房价定为155元时,可获得最高收入18018.75元。此时,相应的入住率为77.5%。
二、入门示例2
1、问题描述
人口统计学家已经发现:每个城市的市中心人口密度最大,离市中心越远人口越稀少、密度越小。最为常见的人口密度模型为(每平方千米人口数),其中
,
为大于0的常数,
是距市中心的距离。如何求某城市的总人口数?
根据相关数据:某城市市中心的人口密度为:。
在距离市中心10km时的人口密度为:。
该城市为半径30km的圆形区域。
2、问题分析
为了确定区间,设市中心位于坐标原点,于是,从而人口密度函数为
。
3、模型求解
先确定人口密度中的常数a,c。
由,
;
,
,可得
,
,
因此人口密度函数为:
从而该城市的总人口数就是人口密度函数的积分,其中积分区域D为,
,即
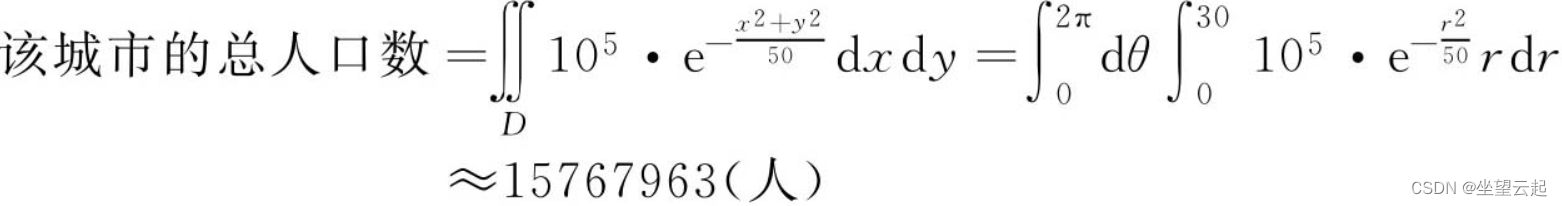
相关文章:
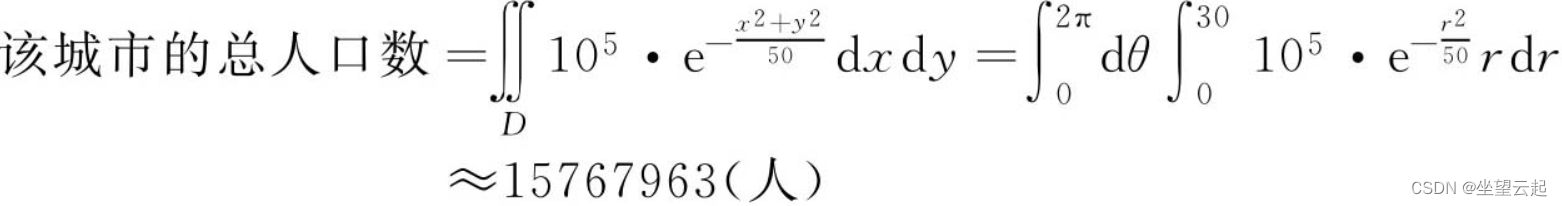
有趣的数学 数学建模入门三 数学建模入门示例两例 利用微积分求解
一、入门示例1 1、问题描述 某宾馆有150间客房,经过一段时间的经营,该宾馆经理得到一些数据:如果每间客房定价为200元,入住率为55%;定价为180元,入住率为65%;定价为160元…...

【Monitor, Maintenance Operation, Script code/prgramme】
Summary of M,M&O,Program JD) Monitor & M&O Symbio信必优) Job chance/opportunities on Dec 12th, 20231.1) Content 招聘JD job description:1.2) suggestions from Ms Liang/Winnie on Wechat app1.3) Java微服务是什么?1.3.1) [URL Java 微服务](…...

python接口自动化测试(单元测试方法)
一、环境搭建 python unittest requests实现http请求的接口自动化Python的优势:语法简洁优美, 功能强大, 标准库跟第三方库灰常强大,建议大家事先了解一下Python的基础;unittest是python的标准测试库,相比于其他测试框架是python目前使用最广…...

【css】划过滚动条,滚动条加宽,划出时,变回原宽度
// 全局的滚动条样式 ::-webkit-scrollbar { //滚动条的宽度width: 4px;height: 6px; }::-webkit-scrollbar-thumb { //滚动条的滑块background-color: rgba(144, 147, 153, 0.6);border-radius: 4px; }// 内容区滚动条划过加宽 .content>div>div::-webkit-scrollbar {…...

飞天使-linux操作的一些技巧与知识点5-ansible之roles
文章目录 roles批量替换文件 role 的依赖关系role 的实际案例 roles tasks 和 handlers ,那怎样组织 playbook 才是最好的方式呢?简 单的回答就是:使用 Roles Roles 基于一个已知的文件结构,去自动的加载 vars,tasks 以…...
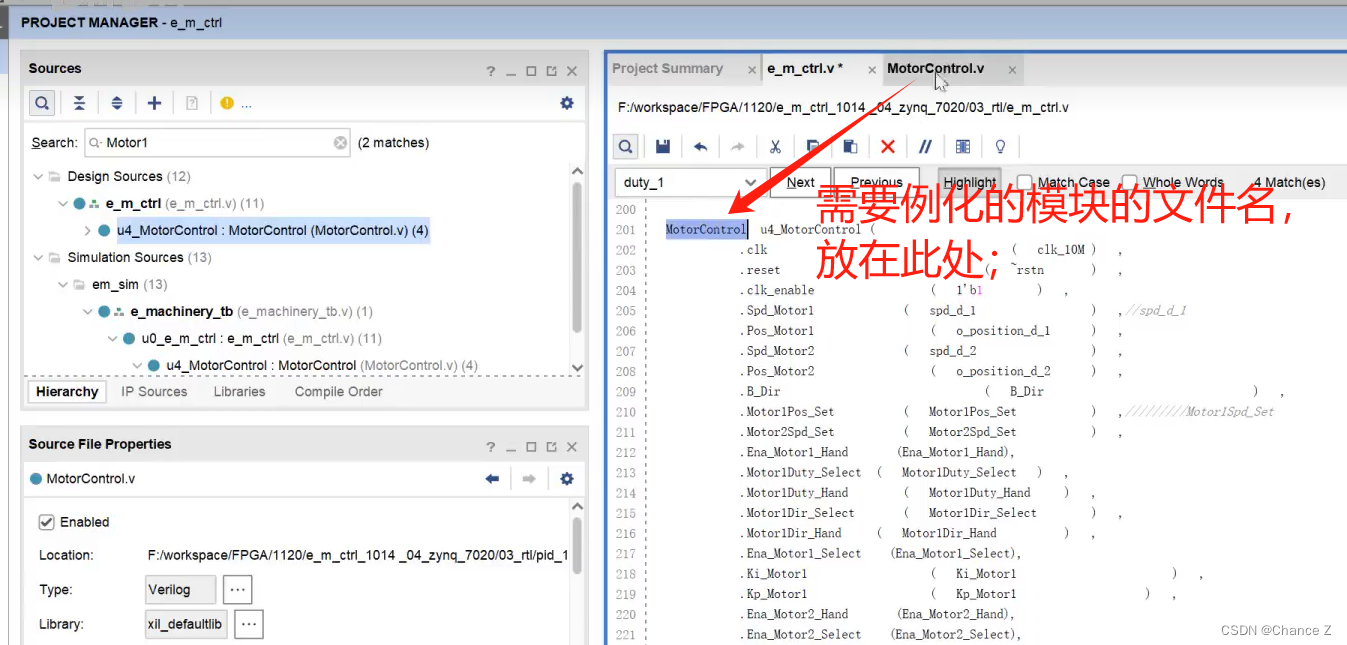
FPGA - 1、Simulink HDL coder模型例化到FPGA
Simulink HDL coder模型例化到FPGA 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成,如何生成可参考右…...
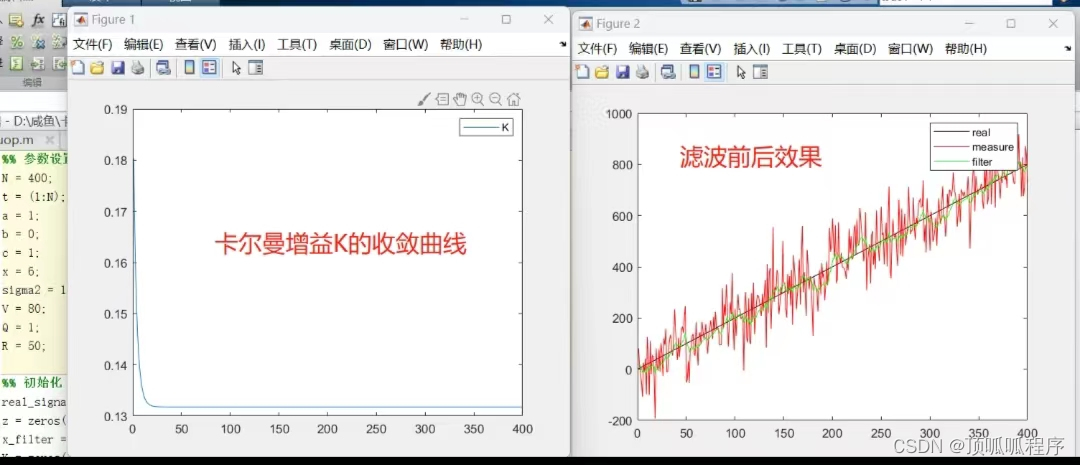
02基于matlab的卡尔曼滤波
基于matlab的卡尔曼滤波,可更改状态转移方程,控制输入,观测方程,设置生成的信号的噪声标准差,设置状态转移方差Q和观测方差R等参数,程序已调通,需要直接拍下。...

基础算法(3):排序(3)插入排序
1.插入排序实现 插入排序的工作原理是:通过构建有序序列,对于未排序数据,在已经排序的序列从后向前扫描,找到位置并插入,类似于平时打扑克牌时,将牌从大到小排列,每次摸到一张牌就插入到正确的位…...
Vue3-18-侦听器watch()、watchEffect() 的基本使用
什么是侦听器 个人理解:当有一个响应式状态(普通变量 or 一个响应式对象)发生改变时,我们希望监听到这个改变,并且能够进行一些逻辑处理。那么侦听器就是来帮助我们实现这个功能的。侦听器 其实就是两个函数ÿ…...
mysql 5.7.34升级到5.7.44修补漏洞
mysql 5.7.34旧版本,漏扫有漏洞,升级到最新版本 旧版本5.7.34在 /home/mysql/mysql中安装 备份旧版本数据还有目录 数据库备份升级 tar -xf mysql-5.7.44-el7-x86_64.tar #覆盖旧版本数据库文件 #注意看看文件是否和你起服务的用户一样 \cp -r mysql-5…...

基于电子密码锁具有掉电存储系统设计
**单片机设计介绍,基于电子密码锁具有掉电存储系统设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 电子密码锁是一种使用电子技术实现开关门的装置,通常由密码输入板、电控锁、控制电路等组成。其中&a…...

清华大学考研复试上机题之二叉树的遍历
问题描述: 编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串:ABC##DE#G##F### 其中#表示的是空格,空格字符代表空树。…...

java全栈体系结构-架构师之路(持续更新中)
Java 全栈体系结构 数据结构与算法实战(已更)微服务解决方案数据结构模型(openresty/tengine)实战高并发JVM虚拟机实战性能调优并发编程实战微服务框架源码解读集合框架源码解读分布式架构解决方案分布式消息中间件原理设计模式JavaWebJavaSE新零售电商项…...

【C语言】超详解strncpystrncatstrncmpstrerrorperror的使⽤和模拟实现
🌈write in front :🔍个人主页 : 啊森要自信的主页 ✏️真正相信奇迹的家伙,本身和奇迹一样了不起啊! 欢迎大家关注🔍点赞👍收藏⭐️留言📝>希望看完我的文章对你有小小的帮助&am…...
【Spring Boot 】Spring Boot 常用配置总结
文章目录 前言1.多环境配置application.propertiesapplication.yaml 2.常用配置3.配置读取4.自定义配置 前言 在涉及项目开发时,通常我们会灵活地把一些配置项集中在一起,如果你的项目不是很大的情况下,那么通过配置文件集中不失为一个很好的…...
Day60力扣打卡
打卡记录 1682分了记录下,希望下回能突破1700捏🤣🤣。作为一个菜鸟😨,知道自己不太行😭👊,从以前的周赛稳定1题到稳定2题🥺,到现在的时有时无的3题ǹ…...
Axure的动态图使用以及说明
认识Axure动态图 Axure动态图是Axure中的一种功能,它允许用户在原型中添加动画效果和交互动作,使原型更加生动和具有真实的用户体验。用户可以通过添加动态图来展示页面过渡、按钮点击、下拉菜单等交互操作的效果。 这是:就是我们今天要叫的…...

力扣 | 437. 路径总和 III
437. 路径总和 III mport java.util.ArrayList; import java.util.List;/*** int的取值范围:* -2^31 ~ 2^31-1* <p>* -2147483648 ~ 2147483647(约等于10的9次方)* <p>* long long的取值范围:* -2^63 ~ (2^63-1&…...
如何部署自己的服务渲染页面为Pdf文档
前言 相信大家都觉得官方发布的文档生成模块https://docs.mendix.com/appstore/modules/document-generation/很有用,它能把Mendix页面像素级导出到Pdf文件中,这对于归档等业务非常有价值。但部署依赖公有云提供的渲染服务,而中国本土用户对…...
)
常用的调试方法(段错误产生原因)
C 语言中常用的调试技巧和 demo C语言中常用的调试方法 打印调试信息 GDB 调试器 编写单元测试 段错误产生原因 初学时两种常用的段错误调试方法 C 语言中常用的调试技巧和 demo 当程序员进行调试时,他们通常会使用一些调试语句或技巧来帮助他们理解代码的执行过程…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
