基础算法(3):排序(3)插入排序
1.插入排序实现
插入排序的工作原理是:通过构建有序序列,对于未排序数据,在已经排序的序列从后向前扫描,找到位置并插入,类似于平时打扑克牌时,将牌从大到小排列,每次摸到一张牌就插入到正确的位置。
实现逻辑:
(1)从第一个元素出现,该元素认为已经被排好序
(2)取出下一个元素,在已经排序的序列中从后向前扫描
(3)如果扫描到某个元素大于取出的新元素,将该元素移到下一个位置
(4)重复(3),直到找到已排序的元素小于或者等于新元素的位置
(5)将新元素插入到该位置后面
(6)重复(2)-(5)
代码实现:
void insertSort(int* arr,int len)
{for(int i=i;i<len;i++){int cur=arr[i];int j=i-1;while(j>=0&&arr[j]>cur){arr[j+1]=arr[j];j--;}arr[j+1]=cur;}
}2.插入排序的时间复杂度
问题规模仍然为n,最好情况是序列是升序,这样只需要比较n-1次,最坏情况是序列是降序,需要比较n(n-1)次,所以时间复杂度为O(n^2)
3.leetcode题目
3.1 删除某些元素后的数组均值

void insertionSort(int *a ,int n){int i,j;int tmp ;for(i = 1; i < n; ++i){for(j = i - 1; j>=0; --j){if(a[j] > a[j+1]){tmp = a[j];a[j] = a[j+1];a[j+1] = tmp; }}}
}
double trimMean(int* arr, int arrSize){insertionSort(arr,arrSize);int cnt = arrSize / 20;double count = 0;for(int i = cnt; i < arrSize - cnt; ++i){count += arr[i];}return count / (arrSize - 2*cnt);
}3.2 去掉最低工资和最高工资后的工资平均值

double average(int* salary,int salarySize){for (int i = 1; i < salarySize; i++) {int tmp = salary[i];int j = i - 1;for (; j >= 0 && tmp < salary[j]; j--) {salary[j + 1] = salary[j];}salary[j + 1] = tmp;}double ans=0;for(int i=1;i<salarySize-1;i++){ans+=salary[i];}return ans/(salarySize-2);
}3.3 学生分数的最小差值

int minimumDifference(int* nums, int numsSize, int k) {for (int i = 1; i < numsSize; i++){int tmp = nums[i];int j = i - 1;for (; j >= 0 && tmp < nums[j]; j--) {nums[j + 1] = nums[j];}nums[j + 1] = tmp;}int ret=100000;for(int i=0;i+k-1<numsSize;i++){int ans=nums[i+k-1]-nums[i];if(ans<ret){ret=ans;}}return ret;
}相关文章:

基础算法(3):排序(3)插入排序
1.插入排序实现 插入排序的工作原理是:通过构建有序序列,对于未排序数据,在已经排序的序列从后向前扫描,找到位置并插入,类似于平时打扑克牌时,将牌从大到小排列,每次摸到一张牌就插入到正确的位…...
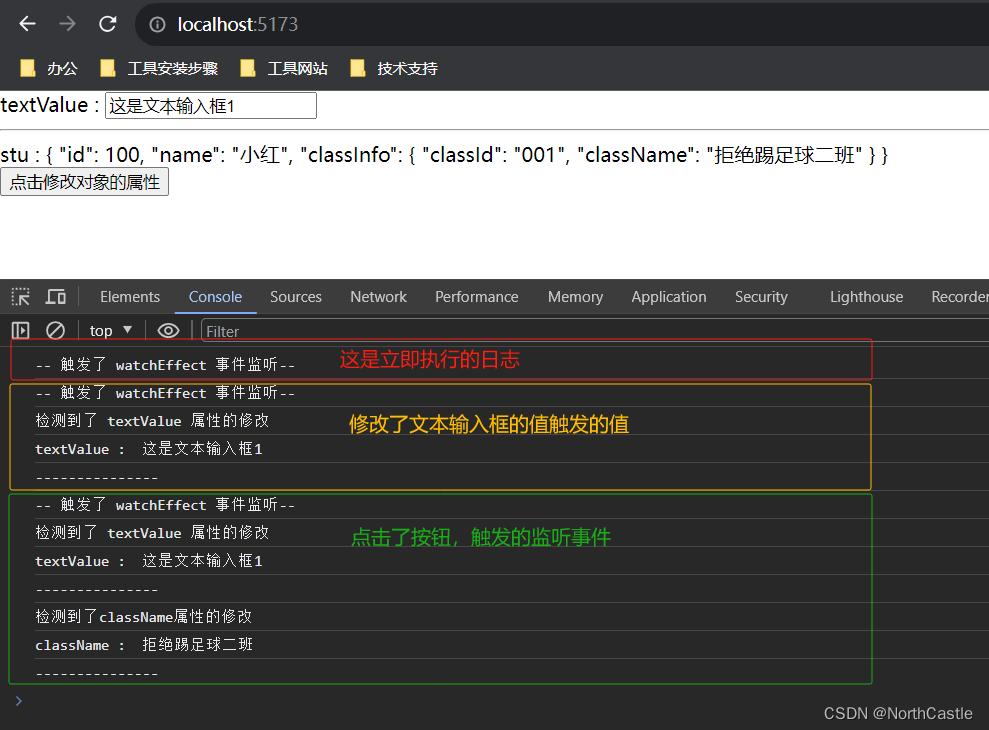
Vue3-18-侦听器watch()、watchEffect() 的基本使用
什么是侦听器 个人理解:当有一个响应式状态(普通变量 or 一个响应式对象)发生改变时,我们希望监听到这个改变,并且能够进行一些逻辑处理。那么侦听器就是来帮助我们实现这个功能的。侦听器 其实就是两个函数ÿ…...
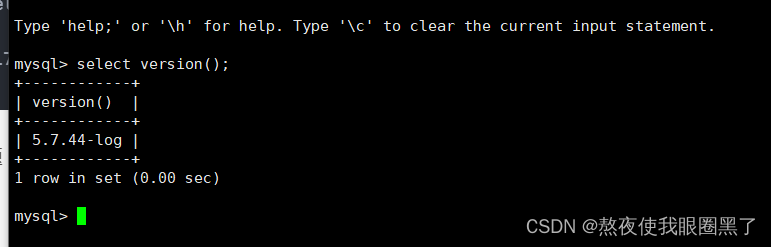
mysql 5.7.34升级到5.7.44修补漏洞
mysql 5.7.34旧版本,漏扫有漏洞,升级到最新版本 旧版本5.7.34在 /home/mysql/mysql中安装 备份旧版本数据还有目录 数据库备份升级 tar -xf mysql-5.7.44-el7-x86_64.tar #覆盖旧版本数据库文件 #注意看看文件是否和你起服务的用户一样 \cp -r mysql-5…...

基于电子密码锁具有掉电存储系统设计
**单片机设计介绍,基于电子密码锁具有掉电存储系统设计 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 电子密码锁是一种使用电子技术实现开关门的装置,通常由密码输入板、电控锁、控制电路等组成。其中&a…...

清华大学考研复试上机题之二叉树的遍历
问题描述: 编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串:ABC##DE#G##F### 其中#表示的是空格,空格字符代表空树。…...

java全栈体系结构-架构师之路(持续更新中)
Java 全栈体系结构 数据结构与算法实战(已更)微服务解决方案数据结构模型(openresty/tengine)实战高并发JVM虚拟机实战性能调优并发编程实战微服务框架源码解读集合框架源码解读分布式架构解决方案分布式消息中间件原理设计模式JavaWebJavaSE新零售电商项…...

【C语言】超详解strncpystrncatstrncmpstrerrorperror的使⽤和模拟实现
🌈write in front :🔍个人主页 : 啊森要自信的主页 ✏️真正相信奇迹的家伙,本身和奇迹一样了不起啊! 欢迎大家关注🔍点赞👍收藏⭐️留言📝>希望看完我的文章对你有小小的帮助&am…...
【Spring Boot 】Spring Boot 常用配置总结
文章目录 前言1.多环境配置application.propertiesapplication.yaml 2.常用配置3.配置读取4.自定义配置 前言 在涉及项目开发时,通常我们会灵活地把一些配置项集中在一起,如果你的项目不是很大的情况下,那么通过配置文件集中不失为一个很好的…...
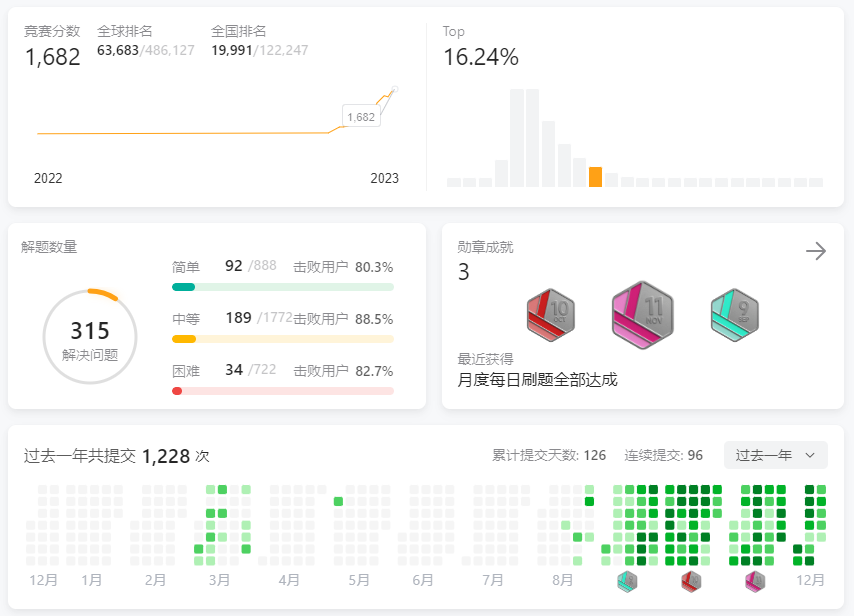
Day60力扣打卡
打卡记录 1682分了记录下,希望下回能突破1700捏🤣🤣。作为一个菜鸟😨,知道自己不太行😭👊,从以前的周赛稳定1题到稳定2题🥺,到现在的时有时无的3题ǹ…...
Axure的动态图使用以及说明
认识Axure动态图 Axure动态图是Axure中的一种功能,它允许用户在原型中添加动画效果和交互动作,使原型更加生动和具有真实的用户体验。用户可以通过添加动态图来展示页面过渡、按钮点击、下拉菜单等交互操作的效果。 这是:就是我们今天要叫的…...

力扣 | 437. 路径总和 III
437. 路径总和 III mport java.util.ArrayList; import java.util.List;/*** int的取值范围:* -2^31 ~ 2^31-1* <p>* -2147483648 ~ 2147483647(约等于10的9次方)* <p>* long long的取值范围:* -2^63 ~ (2^63-1&…...
如何部署自己的服务渲染页面为Pdf文档
前言 相信大家都觉得官方发布的文档生成模块https://docs.mendix.com/appstore/modules/document-generation/很有用,它能把Mendix页面像素级导出到Pdf文件中,这对于归档等业务非常有价值。但部署依赖公有云提供的渲染服务,而中国本土用户对…...
)
常用的调试方法(段错误产生原因)
C 语言中常用的调试技巧和 demo C语言中常用的调试方法 打印调试信息 GDB 调试器 编写单元测试 段错误产生原因 初学时两种常用的段错误调试方法 C 语言中常用的调试技巧和 demo 当程序员进行调试时,他们通常会使用一些调试语句或技巧来帮助他们理解代码的执行过程…...

[云原生] Docker 入门指南:镜像、容器、卷和网络解析
Docker 是一种流行的容器化平台,它以其强大的功能和易用性在软件开发和部署领域广受欢迎。本文将带领您逐步探索 Docker 中的四个核心概念:镜像、容器、卷和网络。通过了解这些概念的是什么、为什么以及如何使用,您将能够更好地理解和利用 Do…...

机器学习-聚类问题
前言 聚类算法又叫做”无监督分类“,目标是通过对无标记训练样本来揭示数据的内在性质及 规律,为进一步的数据分析提供基础。 Kmeans 作为聚类算法的典型代表,Kmeans可以说是最简单的聚类算法,没有之一,那她是怎么完…...

leetcode9.回文数java解法
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。 回文数是指正序(从左向右)和倒序(从右向左&…...
图论专栏一《图的基础知识》
图论(Graph Theory)是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定关系,用点代表实体,用连接两点的线表示两个实体间具有的…...

得帆云为玉柴打造CRM售后服务管理系统,实现服务全过程管理|基于得帆云低代码的CRM案例系列
广西玉柴机器股份有限公司 广西玉柴机器股份有限公司始建于1992年,是国内行业首家赴境外上市的中外合资企业,产品远销亚欧美非等180多个国家和地区。公司总部设在广西玉林市,下辖11家子公司,生产基地布局广西、江苏、安徽、山东等…...

智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蝠鲼觅食算法4.实验参数设定5.算法结果6.…...

vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件
vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件 1. vue2 自定义组件的 v-model vue2官网,自定义组件官方解释:一个组件上的 v-model 默认会利用名为 value 的 prop 和名为 input 的事件上代码代码中使用了 element-ui 子组件 使用默…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
