图论专栏一《图的基础知识》
图论(Graph Theory)是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定关系,用点代表实体,用连接两点的线表示两个实体间具有的某种关系。
相比矩阵、张量、序列等结构,图结构可以有效建模和解决社会关系、交通网络、文法结构和论文引用等需要考虑实体间关系的各种实际问题。因此,为了能够有效利用图结构这种工具,我们必须要对图的定义、类型和性质有一定的认识。
概念
图是由顶点(vertex)和边(edge)组成的数据结构
如下图:
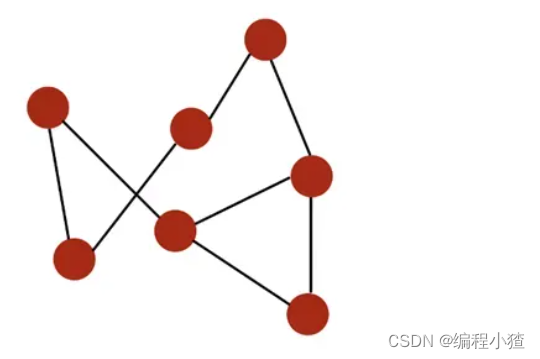
节点(node)用红色标出,通过黑色的边(edge)连接。
图可用于表示:
- 社交网络
- 网页
- 生物网络
- …
我们可以在图上执行怎样的分析?
- 研究拓扑结构和连接性
- 群体检测
- 识别中心节点
- 预测缺失的节点
- 预测缺失的边
- …
为了方便大家的学习,下面我先来介绍一下图的基本术语。
基本术语
图的分类
有向图(Directed Graph):
- 在有向图中,每条边都有一个方向,从一个顶点指向另一个顶点。
- 如果顶点 A 到顶点 B 有一条有向边,则我们称顶点 A 直接指向顶点 B。这意味着从顶点 A 出发可以到达顶点 B,但反之则不一定成立。
- 有向图常用于表示具有方向性关系的问题,例如交通流向、网页链接、任务依赖关系等。
无向图(Undirected Graph):
- 在无向图中,边没有方向,即连接两个顶点的边可以被看作是双向的。
- 如果顶点 A 与顶点 B 之间有一条边,那么顶点 A 与顶点 B 之间是相互连通的,可以双向移动。
- 无向图常用于表示无方向性关系的问题,例如社交网络中的好友关系、道路交通图等。
无向完全图:无向图中,任意两个顶点之间都存在边。
有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。
简单图:图中不存在顶点到其自身的边,且同一条边不重复出现。
稀疏图:有很少条边。
稠密图:有很多条边。
子图(Subgraph):假设G=(V,{E})和G‘=(V',{E'}),如果V'包含于V且E'包含于E,则称G'为G的子图。
边
边:顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边(Edge):若顶点V1到V2之间的边没有方向,则称这条边为无向边。
无向图(Undirected graphs):图中任意两个顶点之间的边都是无向边。(A,D)=(D,A)
对于无向图G来说,G1=(V1,{E1}),其中顶点集合V1={A,B,C,D};边集和E1={(A,B),(B,C),(C,D),(D,A),(A,C)}

有向边:若从顶点V1到V2的边有方向,则称这条边为有向边,也称弧(Arc)。用<V1,V2>表示,V1为弧尾(Tail),V2为弧头(Head)。(V1,V2)≠(V2,V1)。
度
度是指与该顶点相邻的边的数量。

例如上图图中
-
A、B、C、E、F 这几个顶点度数为 2
-
D 顶点度数为 4
有向图中,细分为入度和出度,参见下图
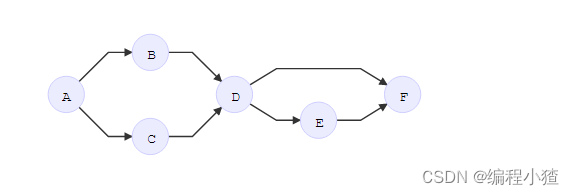
分析上图可知个顶点的出度与入度如下:
A (2 out / 0 in) 两个出度,没有入度
B、C、E (1 out / 1 in)
D (2 out / 2 in)
F (0 out / 2 in)
权
边可以有权重,代表从源顶点到目标顶点的距离、费用、时间或其他度量。

路径
路径被定义为从一个顶点到另一个顶点的一系列连续边,例如上图中【北京】到【上海】有多条路径。
北京 - 上海
北京 - 武汉 - 上海
路径长度
不考虑权重,长度就是边的数量
考虑权重,一般就是权重累加
环
在有向图中,从一个顶点开始,可以通过若干条有向边返回到该顶点,那么就形成了一个环。
如下图:

图的连通性
如果两个顶点之间存在路径,则这两个顶点是连通的,所有顶点都连通,则该图被称之为连通图,若子图连通,则称为连通分量。
graph LRA --- BA --- CC --- DD --- EB --- EF --- GG --- HH --- FI --- J根据上面给出的点与点之间的连通性,可得出下图:

强连通分量:有向图中的极大强连通子图。
生成树:无向图中连通且n个顶点n-1条边叫生成树。
有向树:有向图中一顶点入度为0其余顶点入度为1。
森林:一个有向图由若干棵有向树构成生成森林。
图的表示方法
图可以用邻接矩阵和邻接表表示
比如说,下面的图

用邻接矩阵可以表示为:
A B C D A 0 1 1 0 B 1 0 0 1 C 1 0 0 1 D 0 1 1 0
用邻接表可以表示为:
A -> B -> C B -> A -> D C -> A -> D D -> B -> C
有向图的例子:
graph LR
A--->B
A--->C
B--->D
C--->D
用邻接矩阵可以表示为:
A B C D
A 0 1 1 0
B 0 0 0 1
C 0 0 0 1
D 0 0 0 0
用邻接表可以表示为:
A - B - C
B - D
C - D
D - empty
图的存储结构
邻接矩阵
邻接矩阵:用两个数组,一个数组保存顶点集,一个数组保存边集。
无向图
无向图的邻接矩阵如图

代码示例
我们先将表示顶点和边的类定义出来
假设顶点的类型为 Vertex:
class Vertex {int value;// 其他顶点属性
}假设边的类型为 Edge:
class Edge {int startVertexId;int endVertexId;// 其他边属性
}class Graph {Vertex[] vertices;Edge[] edges;int[][] adjacencyMatrix;public Graph(Vertex[] vertices, Edge[] edges) {this.vertices = vertices;this.edges = edges;this.adjacencyMatrix = new int[vertices.length][vertices.length];// 初始化邻接矩阵,将相应位置设为 1 表示边的连接关系for (Edge edge : edges) {adjacencyMatrix[edge.startVertexId][edge.endVertexId] = 1;// 如果是无向图还需要设置对称位置adjacencyMatrix[edge.endVertexId][edge.startVertexId] = 1;}}
}有向图
有向图的邻接矩阵如图

代码示例
class Digraph {Vertex[] vertices;Edge[] edges;int[][] adjacencyMatrix;public Digraph(Vertex[] vertices, Edge[] edges) {this.vertices = vertices;this.edges = edges;this.adjacencyMatrix = new int[vertices.length][vertices.length];// 初始化邻接矩阵,将相应位置设为 1 表示边的连接关系for (Edge edge : edges) {adjacencyMatrix[edge.startVertexId][edge.endVertexId] = 1;}}
}邻接表
邻接表:数组与链表相结合的存储方法。
邻接表表示法(链式)表示如下图:

- 顶点: 按编号顺序将顶点数据存储在一维数组中。
- 关联同一顶点的边: 用线性链表存储。
- 如果有边\弧的信息,还可以在表结点中增加一项,

无向图
无向图的邻接表如下图:

特点:
- 邻接表不唯一
- 若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适宜存储稀疏图。
- 无向图中顶点vi的度为第i个单链表中的结点数
代码示例
import java.util.ArrayList;
import java.util.List;class Graph {int numVertices;List<List<Integer>> adjacencyList;public Graph(int numVertices) {this.numVertices = numVertices;this.adjacencyList = new ArrayList<>(numVertices);// 初始化邻接表for (int i = 0; i < numVertices; i++) {adjacencyList.add(new ArrayList<>());}}public void addEdge(int src, int dest) {// 添加双向边的连接关系adjacencyList.get(src).add(dest);adjacencyList.get(dest).add(src);}
}
有向图

特点:
- 顶点vi的出度为第i个单链表中的结点个数。
- 顶点vi的入度为整个单链表中邻接点域值是i-1的结点个数。
- 找出度易,找入度难
逆邻接表:

逆邻接表特点:
- 顶点vi的入度为第i个单链表中的结点个数。
- 顶点vi的出度为整个单链表中邻接点域值是i-1的结点个数。
- 找入度易,找出度难。
当邻接表的存储结构形成后,图便唯一确定。
代码示例:
import java.util.ArrayList;
import java.util.List;class Digraph {int numVertices;List<List<Integer>> adjacencyList;public Digraph(int numVertices) {this.numVertices = numVertices;this.adjacencyList = new ArrayList<>(numVertices);// 初始化邻接表for (int i = 0; i < numVertices; i++) {adjacencyList.add(new ArrayList<>());}}public void addEdge(int src, int dest) {// 添加单向边的连接关系adjacencyList.get(src).add(dest);}
}图的遍历
广度优先遍历(BFS)
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS。是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。
其实他本意就是,先遍历一个节点,然后遍历那个节点所连接的的周边节点,之后再一个结点一个结点的往外遍历,重复循环。
下面举个例子:

这张图,我们设从“3”开始遍历,运用广度优先的方法,那么我们所得到的遍历顺序为3,2,3,4,5,1
深度优先遍历(DFS)
所谓DFS,就是从起点开始,找准一个方向直到走不了为止,然后再原路返回,再找到一个能走的地方继续走的思路。
下面举个例子:
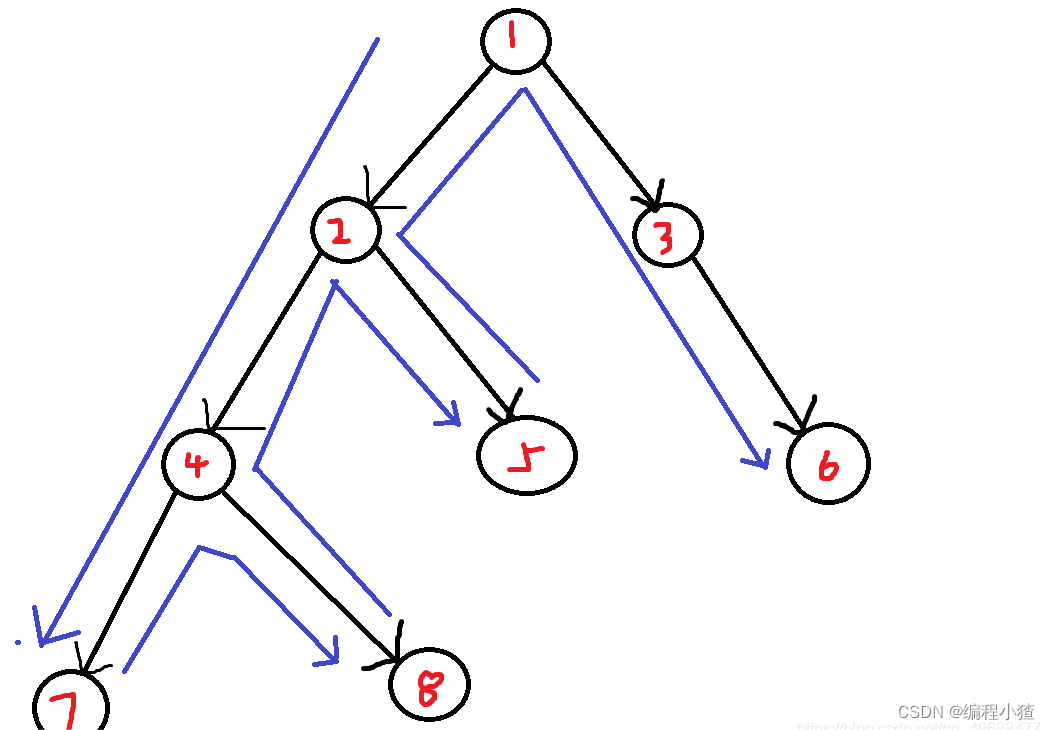
遍历顺序为:1,2,4,7,8,5,3,6
这里这两种算法,我只是概述一下,后面我还会写两篇博文来专门讲这两种遍历方式
上面差不多就是刷图论的题所需要具备的图的基础知识了,后续我会继续更新一些我在刷图论题的一些体会。
相关文章:

图论专栏一《图的基础知识》
图论(Graph Theory)是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些实体之间的某种特定关系,用点代表实体,用连接两点的线表示两个实体间具有的…...

得帆云为玉柴打造CRM售后服务管理系统,实现服务全过程管理|基于得帆云低代码的CRM案例系列
广西玉柴机器股份有限公司 广西玉柴机器股份有限公司始建于1992年,是国内行业首家赴境外上市的中外合资企业,产品远销亚欧美非等180多个国家和地区。公司总部设在广西玉林市,下辖11家子公司,生产基地布局广西、江苏、安徽、山东等…...

智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蝠鲼觅食算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蝠鲼觅食算法4.实验参数设定5.算法结果6.…...

vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件
vue2 以及 vue3 自定义组件使用 v-model使用默认值以及自定义事件 1. vue2 自定义组件的 v-model vue2官网,自定义组件官方解释:一个组件上的 v-model 默认会利用名为 value 的 prop 和名为 input 的事件上代码代码中使用了 element-ui 子组件 使用默…...
《PCL多线程加速处理》-滤波-统计滤波
《PCL多线程加速处理》-滤波-统计滤波 一、效果展示二、实现方式三、代码一、效果展示 提升速度随着点云越多效果越明显 二、实现方式 1、原始的统计滤波实现方式 #include <pcl/filters/statistical_outlier_removal.h>pcl::PointCloud<pcl::PointXYZ...

插入排序——直接插入排序和希尔排序(C语言实现)
文章目录 前言直接插入排序基本思想特性总结代码实现 希尔排序算法思想特性总结代码实现 前言 本博客插入排序动图和希尔排序视频参考大佬java技术爱好者,如有侵权,请联系删除。 直接插入排序 基本思想 直接插入排序是一种简单的插入排序法ÿ…...
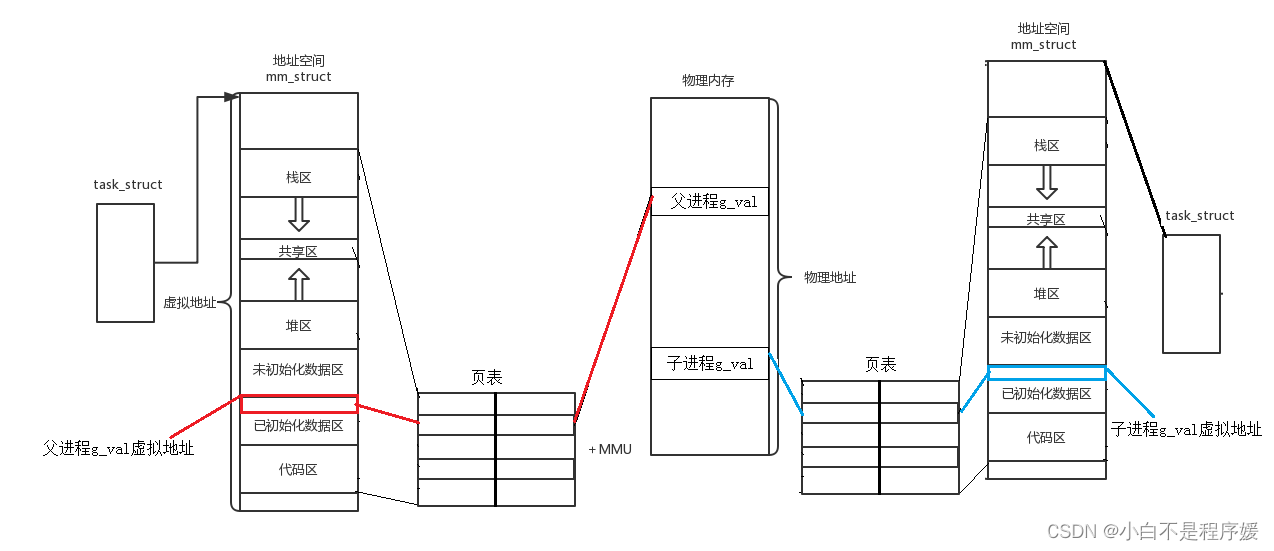
【Linux系统化学习】进程地址空间 | 虚拟地址和物理地址的关系
个人主页点击直达:小白不是程序媛 Linux专栏:Linux系统化学习 代码仓库:Gitee 目录 虚拟地址和物理地址 页表 进程地址空间 进程地址空间存在的意义 虚拟地址和物理地址 我们在学习C/C的时候肯定都见过下面这张有关于内存分布的图片&a…...
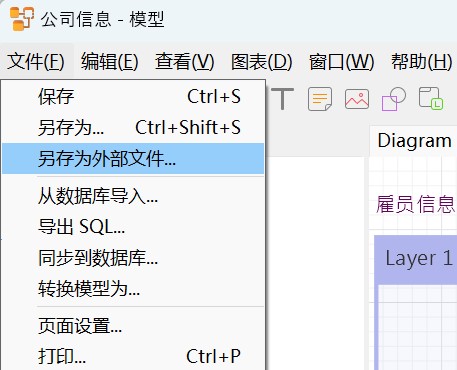
Navicat 技术指引 | 适用于 GaussDB 分布式的模型功能
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…...

四十五、Redis主从
目录 1、数据同步原理 (1)全量同步 (2)增量同步 (3)优化Redis主从集群 (4)什么时候执行全量同步 (5)什么时候执行增量同步 2、流程 1、数据同步原理 &…...

Spring源码学习一
IOC容器概述 ApplicationContext接口相当于负责bean的初始化、配置和组装的IoC容器. Spring为ApplicationContext提供了一些开箱即用的实现, 独立的应用可以使用 ClassPathXmlApplicationContext或者FileSystemXmlApplicationContext,web应用在web.xml配置监 听&am…...

小红书种草和抖音传播区别是什么?
目前品牌较为关注的2大平台小红书和抖音,两者在种草方面存在一些明显的区别。本次就存量竞争、种草形式和种草策略这三个方面入手进行分析,今天和大家分享下小红书种草和抖音传播区别是什么? 一、存量竞争下的2大平台 2个都是属于存量竞争下的…...

论文阅读《Parameterized Cost Volume for Stereo Matching》
论文地址:https://openaccess.thecvf.com/content/ICCV2023/papers/Zeng_Parameterized_Cost_Volume_for_Stereo_Matching_ICCV_2023_paper.pdf 源码地址:https://github.com/jiaxiZeng/Parameterized-Cost-Volume-for-Stereo-Matching 概述 现有的立体匹…...
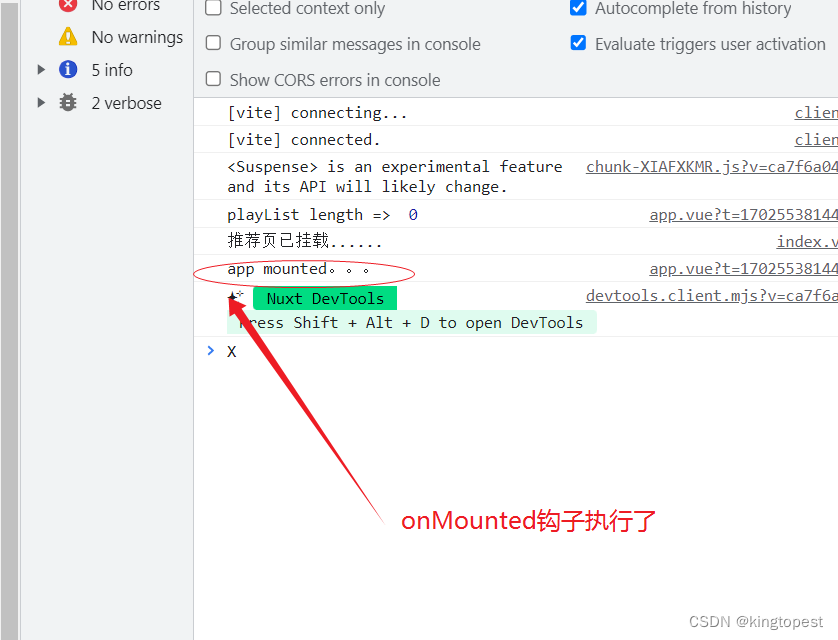
解决nuxt3中vue3生命周期钩子onMounted不执行的问题
看到这篇文章算你运气好!因为只有我才能给你答案!看到就赚到,这就是缘分 因为vue3迁移nuxt3是一个非常困难和痛苦的过程,中间会有各种报错,各种不兼容,各种乱七八糟但是你又找不到答案的问题。 而且你一定…...

Win32 HIWORD和LOWORD宏学习
HIWORD是High Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于高位的两个字节,即一个word长的数据; LOWORD是Low Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于低位的两个字节,即一个word长的数据; Win32编程常用; Win32窗口编程中,收到 WM_S…...

Axure官方软件安装、汉化保姆级教程(带官方资源下载)
1.下载汉化包 百度云链接:https://pan.baidu.com/s/1lluobjjBZvitASMt8e0A_w?pwdjqxn 提取码: jqxn 2.解压压缩包 3.安装Axure 进行安装 点击next 打勾,然后next, 默认是c盘,修改成自己的文件夹(不要什么都放c盘里…...

qt-C++笔记之addAction和addMenu的区别以及QAction的使用场景
qt-C笔记之addAction和addMenu的区别以及QAction的使用场景 code review! 文章目录 qt-C笔记之addAction和addMenu的区别以及QAction的使用场景1.QMenu和QMenuBar的关系与区别2.addMenu和addAction的使用场景区别3.将QAction的信号连接到槽函数4.QAction的使用场景5.将例1修改…...

nodejs 管道通讯
概述 2个nodejs程序的一种通讯方式,管道通讯,跟其他语言一样,管道通讯是一种特殊的socket通讯,普通的socket通讯是通过监听端口触发通讯机制,管道通讯是通过监听文件的方式进行通讯,一般用于单机的多进程通…...

k8s常用命令及示例(三):apply 、edit、delete
k8s常用命令及示例(三):apply 、edit、delete 1. kubectl apply -f 命令:从yaml文件中创建资源对象。 -f 参数为强制执行。kubectl apply和kubectl create的区别如下:kubectl create 和 kubectl apply 是 Kubernetes 中两个常用的命令&…...

前端页面显示的时间格式为:2022-03-18T01:46:08.000+00:00 如何转换为:年-月-日,并根据当前时间判断为几天前
由于后端每条博文的发表时间是以“xxxx—xx—xxxx:xx:xx”的形式显示的, 现在要在前端改成“xxxx年xx月xx日”的形式。 并对10分钟内发表的显示“刚刚”,对24小时内发表的显示“小时前”。 超过24小时,小于48小时,显示“1天前”。…...
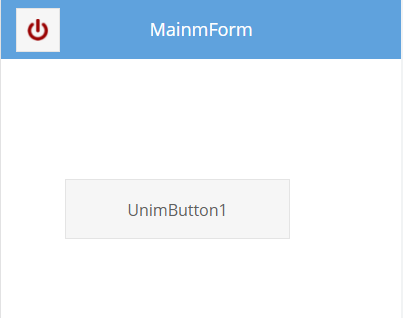
UniGui使用CSS移动端按钮标题垂直
unigui移动端中按钮拉窄以后,标题无法垂直居中,是因为标题有一个padding属性,在四周撑开一段距离。会变成这样: 解决方法,用css修改padding,具体做法如下 首先给button的cls创建一个cls,例如 然后添加css&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
