论文阅读《Parameterized Cost Volume for Stereo Matching》
论文地址:https://openaccess.thecvf.com/content/ICCV2023/papers/Zeng_Parameterized_Cost_Volume_for_Stereo_Matching_ICCV_2023_paper.pdf
源码地址:https://github.com/jiaxiZeng/Parameterized-Cost-Volume-for-Stereo-Matching
概述

现有的立体匹配方法针对大视差场景预测时时间和显存消耗成本大,限制了模型在现实世界的应用。先前的研究工作主要聚焦于使用局部信息的动态代价体进行迭代优化,此类方法虽可以节省内存,但由于缺乏全局视差视野而需要更多的迭代步数才能收敛到目标视差,如图1(a) 所示。为此,文中提出使用高斯分布来编码视差空间。而使用带有固定小方差的单高斯分布对视差空间编码时,每个像素的视差值都服从同一个参数相同的高斯分布,这样的分布对整个视差空间的观察视野有限,不能覆盖整个视差空间,当初始视差与目标视差距离过远时模型难以收敛到目标视差(或需要付出更多的时间成本)。而使用多元高斯分布来表示视差空间可以使得每个像素的视差值都服从一个由多个高斯分布组成的混合分布。这样的分布在视差空间中的视野是全局的,可以均匀地初始化在整个视差范围内。因此,使用多高斯分布可以在迭代开始的阶段迅速收敛。在视差局部调优阶段,多高斯分布的参数会变小,使得模型可以在局部视差空间进行更精细化的匹配。
为此,文中提出一种参数化的代价体,该代价体使用多元高斯分布编码每个像素的视差空间(参数化为权重、均值、方差),并使用JS散度进行优化。文中提出了一个前馈微分模块来实现该优化过程,该过程包含四个步骤:(1)使用初始的均值与方差采样视差候选值。(2)使用采样的视差候选值计算匹配代价,并基于该代价与多层GRU预测一个优化步长(3)用预测的步长更新三个视差空间的参数,并将更新后的参数作为下个迭代阶段的初始值,同时用均值的加权平均(多元高斯分布的期望)作为当前迭代阶段的视差输出。此外,由于前馈优化在收敛阶段容易发生局部震荡,针对该问题,文中引入基于一个不确定性感知的细化模块来修正最后一次迭代的错误结果。该确定性由权重与方差计算而来,并作为视差结果置信度的度量。该置信度可以指导视差从高可靠性区域扩散传播到低可靠区域。在合成数据集与真实世界数据集上的实验结果表明,该方法可以实现实时推理与SOTA性能。
模型架构

Parameterized Cost Volume
公式化:不妨使用 C ( x ) = c x d C(x)=c_{x}^{d} C(x)=cxd 表示代价体,传统的方法是密集地从一个离散的视差分布 { 0 , 1 , … , D − 1 } \{0, 1, …, D − 1\} {0,1,…,D−1}中枚举所有可能的视差候选 d d d,,这样会消耗大量的内存和计算资源。相比之下,动态代价体积的方法只从一个初始化的视差 d ∈ N d ~ d\in N_{\tilde{d}} d∈Nd~中采样视差候选 d d d,其中 N N N表示邻域的大小,这样可以减少内存和计算的开销,但是需要多次迭代来逼近真实的视差。在本文中,作者使用一个参数化的代价体(多元高斯分布)来编码视差空间:
C ( x , θ ) = { c x d ( θ ) } , d ( θ ) ∼ ∑ i = 1 i = M α i N ( μ i , σ i 2 ) . (1) \begin{aligned} C(x,\theta)& =\{c_{x}^{d(\theta)}\}, \\ d(\theta)& \sim\sum_{i=1}^{i=M}\alpha_i\mathcal{N}(\mu_i,\sigma_i^2). \end{aligned}\tag{1} C(x,θ)d(θ)={cxd(θ)},∼i=1∑i=MαiN(μi,σi2).(1)
其中, θ = { α i , μ i , σ i } i = 1 M \theta=\{\alpha_i,\mu_i,\sigma_i\}_{i=1}^M θ={αi,μi,σi}i=1M 为多元高斯分布的参数,包括权重参数 α = { α i } i = 1 M \alpha=\{\alpha_{i}\}_{i=1}^{M} α={αi}i=1M, 均值 μ = { μ i } i = 1 M \mu=\{\mu_{i}\}_{i=1}^{M} μ={μi}i=1M 与标准差(文中用标准差来替代方差) σ = { σ i } i = 1 M \sigma=\{\sigma_{i}\}_{i=1}^{M} σ={σi}i=1M。 M M M 为高斯分布的数量。 ∼ \sim ∼ 表示从分布中采样,且有 ∑ i = 1 M α i = 1 \sum_{i=1}^{M}\alpha_{i}=1 ∑i=1Mαi=1。通过从多个高斯分布中系数采样可以保持动态代价体的高效性,且通过在整个视差范围中均匀初始化多个高斯分布可以获得一个全局视差视野,有利于模型快速收敛到目标视差。
优化:为了高效地对高斯分布参数进行学习,将真实视差定义为一个目标高斯分布 N ( μ g t , σ g t ) \mathcal{N}(\mu_{gt},\sigma_{gt}) N(μgt,σgt) 并基于JS散度训练使得多元高斯分布的参数逼近于目标分布,其中 μ g t \mu_{gt} μgt 为目标视差值, σ g t \sigma_{gt} σgt 为预定义的参数,模型的优化目标可以表示为:
m i n 1 2 ( F ( N g t ∣ ∣ ∑ i = 1 i = M α i N i ) + F ( ∑ i = 1 i = M α i N i ∣ ∣ N g t ) ) , s . t . ∑ i = 1 i = M α i = 1 , (2) \begin{gathered}min~\frac12(F(\mathcal{N}_{gt}||\sum_{i=1}^{i=M}\alpha_i\mathcal{N}_i)+F(\sum_{i=1}^{i=M}\alpha_i\mathcal{N}_i||\mathcal{N}_{gt})),\\s.t.~\sum_{i=1}^{i=M}\alpha_i=1,\end{gathered}\tag{2} min 21(F(Ngt∣∣i=1∑i=MαiNi)+F(i=1∑i=MαiNi∣∣Ngt)),s.t. i=1∑i=Mαi=1,(2)
其中 F ( P ∣ ∣ Q ) = ∑ d ∈ D P ( d ) l o g P ( d ) Q ( d ) F(P||Q)=\sum_{d\in\mathcal{D}}P(d)log\frac{P(d)}{Q(d)} F(P∣∣Q)=∑d∈DP(d)logQ(d)P(d) 为KL 散度。 N i \mathcal{N}_i Ni 为 N ( μ i , σ i 2 ) \mathcal{N}(\mu_{i},\sigma_{i}^{2}) N(μi,σi2) 的缩写,然后将有约束的优化问题写成对应的拉格朗日函数:
L = 1 2 ( F ( N g t ∣ ∣ ∑ i = 1 i = M α i N i ) + F ( ∑ i = 1 i = M α i N i ∣ ∣ N g t ) ) + λ ( ∑ i = 1 i = M α i − 1 ) , (3) \begin{aligned}L&=\frac12(F(\mathcal{N}_{gt}||\sum_{i=1}^{i=M}\alpha_i\mathcal{N}_i)+F(\sum_{i=1}^{i=M}\alpha_i\mathcal{N}_i||\mathcal{N}_{gt}))\\&+\lambda(\sum_{i=1}^{i=M}\alpha_i-1),\end{aligned}\tag{3} L=21(F(Ngt∣∣i=1∑i=MαiNi)+F(i=1∑i=MαiNi∣∣Ngt))+λ(i=1∑i=Mαi−1),(3)
其中 λ \lambda λ 表示拉格朗日乘数。求解这个等式之前,先引入两个必要的公理。
公理1 给定两个高斯分布 N p \mathcal{N}_{p} Np 与 N q \mathcal{N}_{q} Nq, 其KL散度 F ( N p ∣ ∣ N q ) F(\mathcal{N}_p||\mathcal{N}_q) F(Np∣∣Nq)为:
F ( N p ∣ ∣ N q ) = l o g σ q σ p + σ p 2 + ( μ p − μ q ) 2 2 σ q 2 − 1 2 . (4) F(\mathcal{N}_p||\mathcal{N}_q)=log\frac{\sigma_q}{\sigma_p}+\frac{\sigma_p^2+(\mu_p-\mu_q)^2}{2\sigma_q^2}-\frac12.\tag{4} F(Np∣∣Nq)=logσpσq+2σq2σp2+(μp−μq)2−21.(4)
公理2 给定两个多元高斯分布 ∑ i = 1 i = M α i p N i p , Q = ∑ i = 1 i = M α i q N i q \sum_{i=1}^{i=M}\alpha_{i}^{p}\mathcal{N}_{i}^{p}, \quad Q =\sum_{i=1}^{i=M}\alpha_{i}^{q}\mathcal{N}_{i}^{q} ∑i=1i=MαipNip,Q=∑i=1i=MαiqNiq,其KL散度的紧凑上界为:
F ( P ∣ ∣ Q ) ≤ ∑ i = 1 i = M F ( α i p ∣ ∣ α i q ) + ∑ i = 1 i = M α i p F ( N i p ∣ ∣ N i q ) . (5) F(P||Q)\leq\sum_{i=1}^{i=M}F(\alpha_i^p||\alpha_i^q)+\sum_{i=1}^{i=M}\alpha_i^pF(\mathcal{N}_i^p||\mathcal{N}_i^q).\tag{5} F(P∣∣Q)≤i=1∑i=MF(αip∣∣αiq)+i=1∑i=MαipF(Nip∣∣Niq).(5)
基于公理2,可以得到公式3中的上界:
L ≤ 1 2 ( ∑ i = 1 i = M F ( 1 M ∣ ∣ α i ) + ∑ i = 1 i = M 1 M F ( N g t ∣ ∣ N i ) + ∑ i = 1 i = M F ( α i ∣ ∣ 1 M ) + ∑ i = 1 i = M α i F ( N i ∣ ∣ N g t ) ) + λ ( ∑ i = 1 i = M α i − 1 ) , (6) \begin{aligned} L\leq \frac12(\sum_{i=1}^{i=M}F(\frac1M||\alpha_i)+\sum_{i=1}^{i=M}\frac1MF(\mathcal{N}_{gt}||\mathcal{N}_i) \\ +\sum_{i=1}^{i=M}F(\alpha_i||\frac{1}{M})+\sum_{i=1}^{i=M}\alpha_iF(\mathcal{N}_i||\mathcal{N}_{gt})) \\ +\lambda(\sum_{i=1}^{\boldsymbol{i}=M}\alpha_i-1), \end{aligned}\tag{6} L≤21(i=1∑i=MF(M1∣∣αi)+i=1∑i=MM1F(Ngt∣∣Ni)+i=1∑i=MF(αi∣∣M1)+i=1∑i=MαiF(Ni∣∣Ngt))+λ(i=1∑i=Mαi−1),(6)
根据公式4,优化 L L L的上界时候,参数 α i , μ i , σ i \alpha_i,\mu_i,\sigma_i αi,μi,σi的梯度可以表示为:
∂ σ i = 1 2 ( σ i 2 − σ g t 2 − Δ 2 M σ i 3 − α i σ i + α i σ i σ g t 2 ) , ∂ μ i = − Δ 2 ( 1 M σ i 2 + α i σ g t 2 ) , ∂ α i = β i + λ , β i = 1 2 ( − 1 M α i + l o g σ g t M α i σ i + σ i 2 + Δ 2 2 σ g t 2 + 1 2 ) , λ = − 1 M ∑ i = 1 i = M β i , Δ = μ g t − μ i . (7) \begin{aligned} \partial\sigma_{i}& =\frac12(\frac{\sigma_i^2-\sigma_{gt}^2-\Delta^2}{M\sigma_i^3}-\frac{\alpha_i}{\sigma_i}+\frac{\alpha_i\sigma_i}{\sigma_{gt}^2}), \\ \partial\mu_{i}& =-\frac\Delta2(\frac1{M\sigma_i^2}+\frac{\alpha_i}{\sigma_{gt}^2}), \\ \partial\alpha_{i}& =\beta_i+\lambda, \\ \beta_{i}& =\frac12(-\frac1{M\alpha_i}+log\frac{\sigma_{gt}M\alpha_i}{\sigma_i}+\frac{\sigma_i^2+\Delta^2}{2\sigma_{gt}^2}+\frac12), \\ \lambda& =-\frac1M\sum_{i=1}^{i=M}\beta_i, \\ \Delta & =\mu_{gt}-\mu_i. \end{aligned}\tag{7} ∂σi∂μi∂αiβiλΔ=21(Mσi3σi2−σgt2−Δ2−σiαi+σgt2αiσi),=−2Δ(Mσi21+σgt2αi),=βi+λ,=21(−Mαi1+logσiσgtMαi+2σgt2σi2+Δ2+21),=−M1i=1∑i=Mβi,=μgt−μi.(7)
因为在推理过程中目标视差 μ g t \mu_{gt} μgt 未知,为此使用类似RAFT的神经网络的方式来不断预测视差参差值,从而逼近目标视差值,因此在 t t t阶段的参数可以表示为:
σ i t + 1 = σ i t − ∂ σ i t , μ i t + 1 = μ i t − ∂ μ i t , α i t + 1 = α i t − ∂ α i t . (8) \begin{aligned}\sigma_i^{t+1}&=\sigma_i^t-\partial\sigma_i^t,\\\mu_i^{t+1}&=\mu_i^t-\partial\mu_i^t,\\\alpha_i^{t+1}&=\alpha_i^t-\partial\alpha_i^t.\end{aligned}\tag{8} σit+1μit+1αit+1=σit−∂σit,=μit−∂μit,=αit−∂αit.(8)
基于动态代价体积的方法在每次迭代时,预测一个步长,用来调整上一次迭代的视差结果,使其更接近真实的视差。这些方法相当于用一个固定方差的单高斯分布来近似视差空间,其中方差的值由真实视差的方差决定。由于单高斯分布的视角有限,这些方法难以在大视差范围内捕捉到全局的信息,因此需要多次迭代才能收敛到真实视差。相比之下,文中所提出的方法用多个高斯分布来表示视差空间,每个高斯分布都有自己的权重,均值和方差,这些参数可以在优化过程中动态更新。这样做的好处是,多高斯分布可以在初始时提供一个全局的视角,覆盖整个视差空间,然后在迭代过程中逐渐收敛到真实视差,实现从粗到细的匹配。此外,多高斯分布之间还可以进行信息交互,加速优化过程,提高收敛速度和准确度。
Feed-forward Differential Module
如图3所示,该模块首先从当前的多高斯分布中采样视差候选值。然后,根据这些视差候选值计算匹配代价,并利用多层GRU 来预测优化步骤。最后,优化步骤用于计算参数的梯度并更新参数。
Multiple Gaussian Sampling:文中选择从当前的多高斯分布中采样视差候选值,每个高斯分布独立采样。具体来说,对于第 i i i个高斯分布,候选值在 [ µ i − 3 σ i , µ i + 3 σ i ] [µ_i − 3σ_i , µ_i + 3σ_i ] [µi−3σi,µi+3σi]的范围内均匀采样。
Optimization Step Prediction:根据视差候选值通过相关性来计算匹配代价。首先,不同高斯分布的代价被几个权值共享的2D卷积层独立编码。编码后的代价以及均值 µ µ µ与方差 σ σ σ和权重 α α α,被拼接作为输入送入多层GRUs,通过一个双层卷积来预测优化步骤 ∆ ∆ ∆。
Parameters Update: 使用梯度下降算法来更新多元高斯分布的参数。由于公式7中的梯度数值不稳定,在更新前对梯度进行裁剪。然后用裁剪后的梯度来更新参数,如公式8所示。为了限制更新后的 α α α在0和1之间,对 α α α进行裁剪和归一化,如下所示:
α ^ i t + 1 = min ( max ( α i t + 1 , 0 ) , 1 ) ∑ i min ( max ( α i t + 1 , 0 ) , 1 ) . (9) \hat{\alpha}_i^{t+1}=\frac{\min(\max(\alpha_i^{t+1},0),1)}{\sum_i\min(\max(\alpha_i^{t+1},0),1)}.\tag{9} α^it+1=∑imin(max(αit+1,0),1)min(max(αit+1,0),1).(9)
更新后的参数用于下一轮的迭代,根据多元高斯分布的期望来预测视差值:
μ ˉ t + 1 = ∑ i = 1 M α ^ i t + 1 μ i t + 1 . (10) \bar{\mu}^{t+1}=\sum_{i=1}^M\hat{\alpha}_i^{t+1}\mu_i^{t+1}.\tag{10} μˉt+1=i=1∑Mα^it+1μit+1.(10)
Uncertainty-aware Refinement Module
为了避免在收敛阶段优化过程中的局部震荡问题,文中引入一个不确定感知精细化模块用于提高视差细节区域的结果。首先将权重 α α α,方差 σ σ σ和均值 µ µ µ输入一系列卷积层,后接一个sigmoid函数,来估计一个不确定性图 U U U。然后将不确定性图和视差图以及左图特征拼接起来,通过卷积层来预测一个残差图 R R R,其中每一层除了最后一层都使用了leaky-relu函数。最后用不确定性图 U U U来指导残差图 R R R和视差图 µ ˉ \bar{µ} µˉ的融合,如下所示:
μ ^ = μ ˉ + R ⋅ U . (11) \hat{\mu}=\bar{\mu}+R\cdot U.\tag{11} μ^=μˉ+R⋅U.(11)
损失函数
为了让预测的高斯分布能逼近目标视差分布,使用 L 1 L1 L1损失在每个阶段约束生成的分布的均值:
L m t = ∑ i = 1 M ∥ μ i t − μ g t ∥ 1 , (12) \mathcal{L}_m^t=\sum_{i=1}^M\|\mu_i^t-\mu_{gt}\|_1,\tag{12} Lmt=i=1∑M∥μit−μgt∥1,(12)
使用 L 1 L1 L1 损失约束最后阶段的视差输出与标签视差:
L d t = ∥ μ ˉ t − μ g t ∥ 1 . (13) \mathcal{L}_d^t=\|\bar{\mu}^t-\mu_{gt}\|_1.\tag{13} Ldt=∥μˉt−μgt∥1.(13)
同样使用 L 1 L1 L1 损失约束精细化后的视差图:
L r = ∥ μ ^ − μ g t ∥ 1 . (14) \mathcal{L}_r=\|\hat{\mu}-\mu_{gt}\|_1.\tag{14} Lr=∥μ^−μgt∥1.(14)
&esmp; 总的损失函数为:
L = ∑ t = 1 T γ t ( L m t + L d t ) + λ L r , (15) \mathcal{L}=\sum_{t=1}^T\gamma^t(\mathcal{L}_m^t+\mathcal{L}_d^t)+\lambda\mathcal{L}_r,\tag{15} L=t=1∑Tγt(Lmt+Ldt)+λLr,(15)
实验结果







相关文章:

论文阅读《Parameterized Cost Volume for Stereo Matching》
论文地址:https://openaccess.thecvf.com/content/ICCV2023/papers/Zeng_Parameterized_Cost_Volume_for_Stereo_Matching_ICCV_2023_paper.pdf 源码地址:https://github.com/jiaxiZeng/Parameterized-Cost-Volume-for-Stereo-Matching 概述 现有的立体匹…...
解决nuxt3中vue3生命周期钩子onMounted不执行的问题
看到这篇文章算你运气好!因为只有我才能给你答案!看到就赚到,这就是缘分 因为vue3迁移nuxt3是一个非常困难和痛苦的过程,中间会有各种报错,各种不兼容,各种乱七八糟但是你又找不到答案的问题。 而且你一定…...

Win32 HIWORD和LOWORD宏学习
HIWORD是High Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于高位的两个字节,即一个word长的数据; LOWORD是Low Word的缩写,作用是取得某个4字节变量(即32位的值)在内存中处于低位的两个字节,即一个word长的数据; Win32编程常用; Win32窗口编程中,收到 WM_S…...

Axure官方软件安装、汉化保姆级教程(带官方资源下载)
1.下载汉化包 百度云链接:https://pan.baidu.com/s/1lluobjjBZvitASMt8e0A_w?pwdjqxn 提取码: jqxn 2.解压压缩包 3.安装Axure 进行安装 点击next 打勾,然后next, 默认是c盘,修改成自己的文件夹(不要什么都放c盘里…...

qt-C++笔记之addAction和addMenu的区别以及QAction的使用场景
qt-C笔记之addAction和addMenu的区别以及QAction的使用场景 code review! 文章目录 qt-C笔记之addAction和addMenu的区别以及QAction的使用场景1.QMenu和QMenuBar的关系与区别2.addMenu和addAction的使用场景区别3.将QAction的信号连接到槽函数4.QAction的使用场景5.将例1修改…...

nodejs 管道通讯
概述 2个nodejs程序的一种通讯方式,管道通讯,跟其他语言一样,管道通讯是一种特殊的socket通讯,普通的socket通讯是通过监听端口触发通讯机制,管道通讯是通过监听文件的方式进行通讯,一般用于单机的多进程通…...

k8s常用命令及示例(三):apply 、edit、delete
k8s常用命令及示例(三):apply 、edit、delete 1. kubectl apply -f 命令:从yaml文件中创建资源对象。 -f 参数为强制执行。kubectl apply和kubectl create的区别如下:kubectl create 和 kubectl apply 是 Kubernetes 中两个常用的命令&…...

前端页面显示的时间格式为:2022-03-18T01:46:08.000+00:00 如何转换为:年-月-日,并根据当前时间判断为几天前
由于后端每条博文的发表时间是以“xxxx—xx—xxxx:xx:xx”的形式显示的, 现在要在前端改成“xxxx年xx月xx日”的形式。 并对10分钟内发表的显示“刚刚”,对24小时内发表的显示“小时前”。 超过24小时,小于48小时,显示“1天前”。…...
UniGui使用CSS移动端按钮标题垂直
unigui移动端中按钮拉窄以后,标题无法垂直居中,是因为标题有一个padding属性,在四周撑开一段距离。会变成这样: 解决方法,用css修改padding,具体做法如下 首先给button的cls创建一个cls,例如 然后添加css&…...

0-50KHz频率响应模拟量高速信号隔离变送器
0-50KHz频率响应模拟量高速信号隔离变送器 型号:JSD TA-2322F系列 高速响应时间,频率响应时间快 特点: ◆小体积,低成本,标准 DIN35mm 导轨安装方式 ◆六端隔离(输入、输出、工作电源和通道间相互隔离) ◆高速信号采集 (-3dB,Min≤ 3.5 uS,订…...
Linux系统下CPU性能问题分析案例
(上) 本文涉及案例来自于学习极客时间专栏《Linux性能优化实战》精心整理而来,案例总结不到位的请各位多多指正。 某个应用的CPU使用率居然达到100%,我该怎么办? 分析过程 使用观察系统CPU使用情况(并按下…...
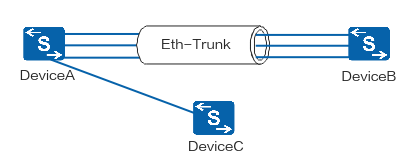
【网络协议】LACP(Link Aggregation Control Protocol,链路聚合控制协议)
文章目录 LACP名词解释LACP工作原理互发LACPDU报文确定主动端确定活动链路链路切换 LACP和PAgP有什么区别?LACP与LAG的关系LACP模式更优于手动模式LACP模式对数据传输更加稳定和可靠LACP模式对聚合链路组的故障检测更加准确和有效 推荐阅读 LACP名词解释 LACP&…...

MATLAB 2018一本通 学习笔记一
vivado暂时可以收一下,而且今天看场景和问题的解决程度,这两天看的还是有效果,需要接下来弄一下matlab。 算法开发、数据可视化、数据分析、数值计算方面,之前搞Python弄过matlib库,觉得差不多,但是实际工…...
文献计量学方法与应用、主题确定、检索与数据采集、VOSviewer可视化绘图、Citespace可视化绘图、R语言文献计量学绘图分析
目录 一、文献计量学方法与应用简介 二、主题确定、检索与数据采集 三、VOSviewer可视化绘图 四、Citespace可视化绘图 五、R语言文献计量学绘图分析 六、论文写作 七、论文投稿 更多应用 文献计量学是指用数学和统计学的方法,定量地分析一切知识载体的交叉…...

C#生成微信支付的Authorization签名认证
//获取签名var Token BuildAuthAsync("GET", body, URL);/// <summary>/// 构造签名串/// </summary>/// <param name"method">HTTP请求方式(全大写)</param>/// <param name"body">API接口…...
平台工程与 DevOps 和 SRE 有何不同?
在现代软件开发和运营的动态领域中 ,平台工程、DevOps 和站点可靠性工程 (SRE) 等术语 经常使用,有时可以互换使用,这常常会导致进入或浏览这些领域的专业人员感到困惑。了解这些概念之间的细微差别对于努力构建强大且可扩展的系统的组织至关…...

算法-只出现一次的数字集合
前言 仅记录学习笔记,如有错误欢迎指正。 题目 记录一道面试过的题目 题目如下: 给定一个数组,内容为1-n的数字,其中每个数字只会出现一次或者多次,请在时间复杂度O(n),空间复杂度O(1)的条件下找出所有出现一次的数…...

Linux,Web网站服务(一)
1.准备工作 为了避免发生端口冲突,程序冲突等现象,建议卸载使用RPM方式安装的httpd [rootnode01 ~]# rpm -e http --nodeps 挂载光盘到/mnt目录 [rootnode01 ~]# mount /dev/cdrom /mnt Apache的配置及运行需要apr.pcre等软件包的支持,因此…...

Monkey工具之fastbot-iOS实践
背景 目前移动端App上线后 crash 率比较高, 尤其在iOS端。我们需要一款Monkey工具测试App的稳定性,更早的发现crash问题并修复。 去年移动开发者大会上有参加 fastbot 的分享,所以很自然的就想到Fastbot工具。 Fastbot-iOS安装配置 准备工…...

我想当个程序员
1、为什么当初选择计算机行业 能从事这个行业,也和当时经济情况有关系。 初中开始感兴趣,大学软件工程专业。大四报的android的培训,后来进的对日外包,没想到签合同当天被辞,非技术原因,性格导致。后来回家…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
