最大公因数,最小公倍数详解
前言
对于初学编程的小伙伴们肯定经常遇见此类问题,而且为之头疼,今天我来给大家分享一下,最大公因数和最小公倍数的求法。让我们开始吧!

文章目录
- 1,最大公因数
- 法1
- 法2
- 法3
- 2,最小公倍数
- 3,尾声
1,最大公因数
首先提起最大公因数大家最先想到的就是辗转相除法。
假如求a,b的最大公因数x。其中a>b。a可以表示为nb+t,那么t=a-nb,因为x是a和b的公因数,将等式两边同时除以x得,t/x=a/x-n*b/x,那么我肯可以知道t/x是个整数,所以x是a和a%b的公因数,那么我们可知那么x也是b和a%b的公因数。所以a和b的最大公约数和b和a%b的最大公约数是一样的。那么我们就可以使用循环的方法求出最大公因数如下:
法1
#include<stdio.h>
int gcd(int a, int b)
{if (a > b)//判断大小事大数除以小数{int temp = a;a = b;b = temp;}while (a % b)//辗转相除{int temp = a;a = b;b = temp%b;}
}
int main()
{int a, b;scanf("%d %d", &a, &b);int ans = gcd(a,b);printf("%d", ans);return 0;
}
那么这样写有点麻烦,我们可以直接使用递归的方法解决而且速度更快。
法2
#include<stdio.h>
int gcd(int a, int b)
{if (a == 0)//当a为0时,b为最大公因数return b;return gcd(b, a%b);
}
int main()
{int a, b;scanf("%d %d", &a, &b);int ans = gcd(a,b);printf("%d", ans);return 0;
}
那么有没有更快的方法呢?当然有!我们都知道位运算的速度比除法运算快的多,那么我肯可以吧代码改成这样。
法3
#include<stdio.h>
int gcd(int a, int b)
{while (b ^= a ^= b ^= a %= b);//连等式是从右往左计算的,我们要知道a^a=0,a^0=a。那么连等式就可以等同于gcd(b,a%b)return a;
}
int main()
{int a, b;scanf("%d %d", &a, &b);int ans = gcd(a,b);printf("%d", ans);return 0;
}
这种算法是最快的
2,最小公倍数
正常求法求最小公倍数可能太过麻烦,但是我们要知道一个定理。假设x是a和b的最大公因数,y是a和b的最小公倍数,那么xy=ab。(如果不明白可以百度一下或者直接背下来当结论用)
所以我们就可以用上面的方法先求出x然后再用y=a*b/x求出y的值。
3,尾声
本期的分享到这里结束,如果觉得博主讲的不错的话请给博主一个点赞一个收藏支持一下,我们下期再见!
相关文章:

最大公因数,最小公倍数详解
前言 对于初学编程的小伙伴们肯定经常遇见此类问题,而且为之头疼,今天我来给大家分享一下,最大公因数和最小公倍数的求法。让我们开始吧! 文章目录 1,最大公因数法1法2法3 2,最小公倍数3,尾声 …...
无脑利用API实现文心一言AI对话功能?(附代码)
前言:在当今数字化的时代,人工智能(AI)技术正在不断演进,为开发者提供了丰富的工具和资源。其中,API(应用程序接口)成为构建强大AI应用的关键组成部分之一。本文将介绍如何利用API来…...

加速数据采集:用OkHttp和Kotlin构建Amazon图片爬虫
引言 曾想过轻松获取亚马逊上的商品图片用于项目或研究吗?是否曾面对网络速度慢或被网站反爬虫机制拦截而无法完成数据采集任务?如果是,那么本文将为您介绍如何用OkHttp和Kotlin构建一个高效的Amazon图片爬虫解决方案。 背景介绍 亚马逊&a…...
lua安装
lua安装 1.Lua介绍 特点:轻量、小巧。C语言开发。开源。 设计的目的:嵌入到应用程序当中,提供灵活的扩展和定制化的功能。 luanginx,luaredis。 2.windows安装lua windows上安装lua: 检查机器上是否有lua C:\U…...
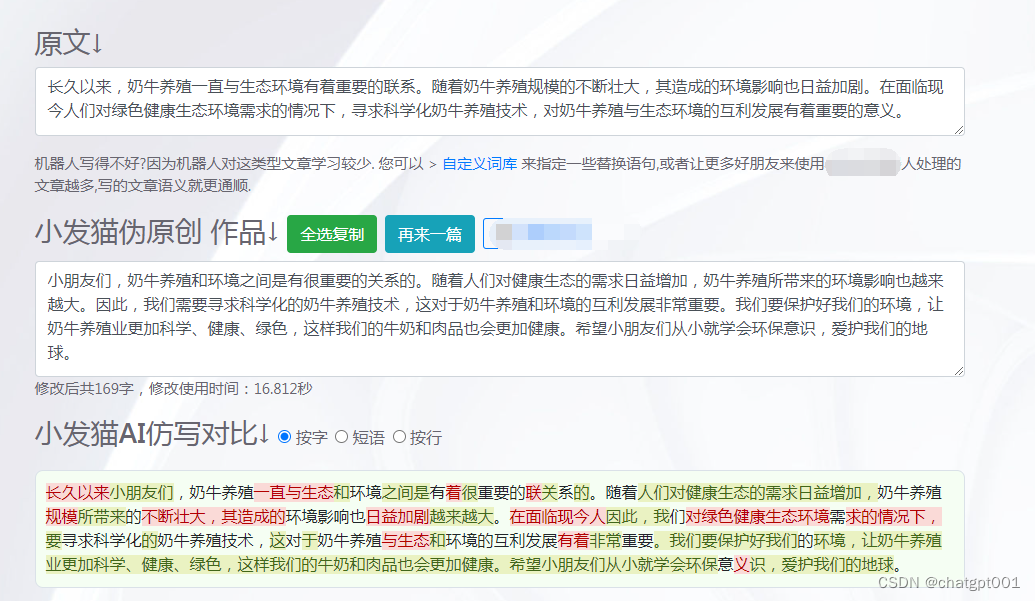
博士毕业需要发表几篇cssci论文
大家好,今天来聊聊博士毕业需要发表几篇cssci论文,希望能给大家提供一点参考。 以下是针对论文重复率高的情况,提供一些修改建议和技巧: 博士毕业需要发表几篇CSSCI论文 背景介绍 CSSCI即“中文社会科学引文索引”,被…...

UDP报文格式详解
✏️✏️✏️各位看官好,今天给大家分享的是 传输层的另外一个重点协议——UDP。 清风的CSDN博客 🛩️🛩️🛩️希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流࿰…...
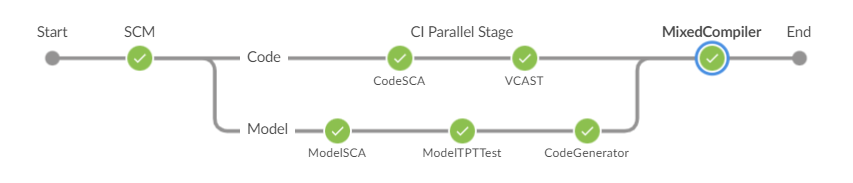
Python自动化测试如何自动生成测试用例?
汽车软件开发自动化测试攻略 随着软件开发在造车行业中占有越来越重要的地位,敏捷开发的思想在造车领域中也逐渐地被重视起来,随之而来的是整车厂对自动化测试需求越来越强烈。本文结合北汇在自动化测试方面的丰富经验,简单介绍一下实施自动…...
)
椋鸟C语言笔记#27:字符串数字提取(atoi、atol、atoll、atof)
萌新的学习笔记,写错了恳请斧正。 目录 atoi 模拟实现 atol与atoll(C99起) atof 合法的浮点值 返回值 使用示例 在stdlib.h中还有几个有意思的字符串函数 它们的功能是将字符串开头的数字提取出来 下面我们具体看一看这几个函数吧 …...

Git 命令使用总结
git init: 在当前目录创建一个新的空Git仓库。git clone [url]: 从远程仓库克隆一个项目到本地。git add [file]: 将文件添加到暂存区。git commit -m “message”: 提交暂存区的文件到本地仓库,并添加一条提交信息。git status: 查看当前工作区的状态(已…...
)
Linux常见面试题30题详细答案解析(二)
1. 如何使用Linux中的包管理器进行软件包依赖管理? Linux中的包管理器如apt、yum等可以自动处理软件包的依赖关系。当安装或升级软件包时,包管理器会自动解决软件包的依赖关系,确保所需的库和工具都已经安装。掌握如何使用包管理器进行依赖管…...
Linux查询指定时间点段日志Linux查询指定文件
Linux服务器高效查询日志查询文件 Ⅰ、常用几种日志查询语法Ⅱ、常用几种查询语法 Ⅰ、常用几种日志查询语法 #查询某日志前xx行日志 head -n 行数 日志文件名 #查询某日志后xx行日志 tail -n 行数 日志文件名 #查询固定时间点日志(前提是这个时间点确实有日志输出…...

2023年华为HCIA认证H12-811题库讲解
在VRP平台上,可以通过下面哪种方式返回到上一条历史命令?( ) A、Ctr1U B、Ctr1P C、左光标 D、上光标 试题答案:BD 试题解析:在VRP系统中,ctrlU为自定义快捷键,ct…...

MacOS上配置Jenkins开机自启动
之前文章有写过,如何在Windows环境下,通过vbsbat脚本的组合拳实现Jenkins的开机自启动,最近换了电脑,又要搭建Jenkins了,顺带整理分享下MacOS上配置Jenkins开机自启动的方法。 具体配置步骤: 打开终端应用…...
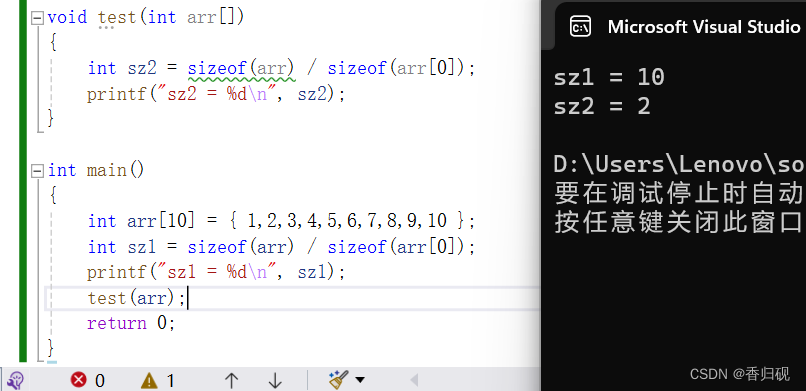
指针相关知识(入门)
通过前面的学习,我们已经对c语言有了一个初步的认识 接下来,我们继续学习。进入下一个阶段,指针。这个部分的知识较多,可能学习起来有些吃力,但是,从简到难,我们慢慢学习。 一.指针的概念 导入…...
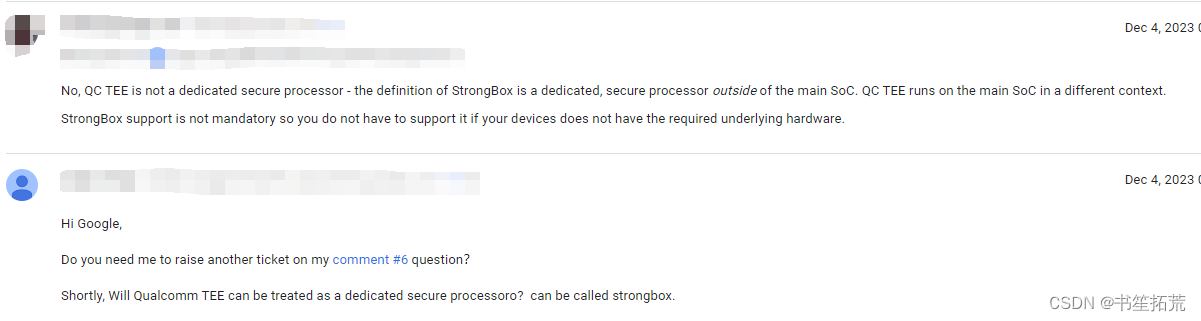
我的NPI项目之Android 安全系列 -- Android Strongbox 初识
从Android9(Pie)开始,Google强烈建议支持Strongbox. 具体描述如下: 一直到目前的Android14. 对应的内容也一并贴出来: 说人话就是Android开始通过独立于主SoC的单元进行密钥存储了。 通常,这样的单元就是我们通常称作的Secure Element(SE)&am…...
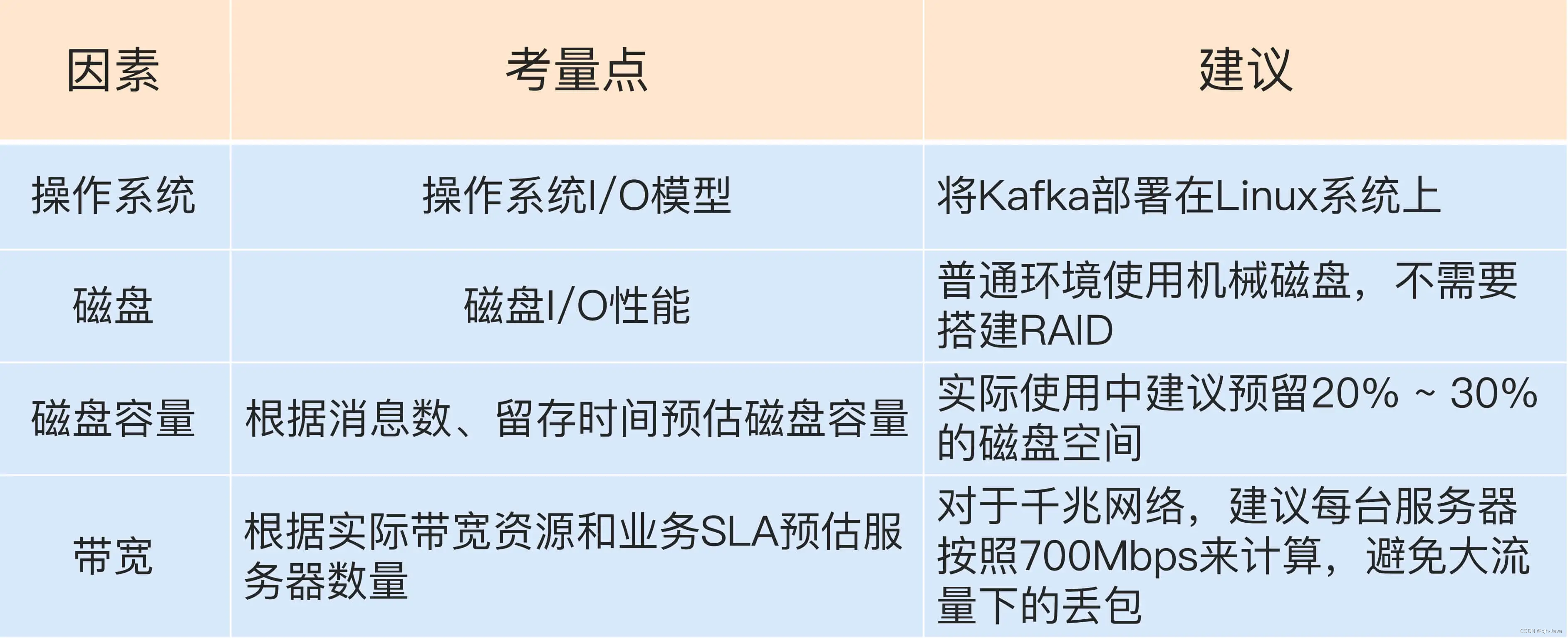
3、Kafka 线上集群部署方案怎么做?
文章目录 1、操作系统的选择1.1、I/O 模型的使用1.2、数据网络传输效率1.3、社区支持度 2、磁盘的选择3、磁盘容量的规划3.1、举例思考本问题:3.2、计算一下:3.3、规划磁盘容量时你需要考虑下面这几个元素: 4、带宽规划4.1、计算 总结 1、操作…...

【Oracle】常用数据库sql记录
文章目录 1、获取指定日期所在年份2、获取指定日期所在月份3、获取指定日期去年同期日期4、获取指定日期所在年份的总天数5、获取年初到指定日期的天数6、除法运算7、递归查询8、REPLACE函数9、DECODE 函数10、聚合函数11、窗口函数11.1 ROW_NUMBER函数11.2 RANK函数11.3 LEAD …...

在线监控网址源码/ 网站监控工具源码/ 网站监控系统源码/定时任务/网站网址URL状态监控神器
源码介绍: 在线监控网址源码、 网站监控工具源码,它作为网站监控系统源码,有定时任务,支持卡密充值,是网站网址URL状态监控神器。让数据库监控更加简单和专业。远程云中监控、实时邮件告警、丰富的指标和图表、分析和…...

【Mysql】myisam和innodb的区别?
0 回答 myisam引擎是5.1版本之前的默认引擎,支持全文检索、压缩、空间函数等,但是不支持事务和行级锁,所以一般用于有大量查询少量插入的场景来使用,而且myisam不支持外键,并且索引和数据是分开存储的。innodb是基于聚簇索引建立的,和myisam相反它支持事务、外键,并且通…...
vue 集成行政区域选择插件region和数据回显
故事:最近,项目需要进行行政区域围栏的绘制,由于老旧项目是利用js保存全国行政区域地址和编码,在选择器select进行匹配显示,但此方法复杂,因此选择集成区域插件region 步骤一:用命令安装region…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
