LeetCode每日一题——2132.用邮票贴满网格图
参考资料:
- 2132. 用邮票贴满网格图 - 力扣(LeetCode)
题目描述
给你一个 m x n 的二进制矩阵 grid ,每个格子要么为 0 (空)要么为 1 (被占据)。
给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中,且满足以下 限制 和 要求 :
- 覆盖所有 空 格子。
- 不覆盖任何 被占据 的格子。
- 我们可以放入任意数目的邮票。
- 邮票可以相互有 重叠 部分。
- 邮票不允许 旋转 。
- 邮票必须完全在矩阵 内 。
如果在满足上述要求的前提下,可以放入邮票,请返回 true ,否则返回 false 。
样例

思路
主要思想:二维前缀和 + 二维差分
由于题目没有限制放入邮票的数量,也允许邮票相互重叠,所以我们应该尽可能地多贴邮票。
假设我们以邮票的左上角 (i,j)为基准粘贴邮票,则该邮票的覆盖范围是 (i.j) ~ (x,y) ,其中 x = i+stampHeight-1, y = j+stampHeight-1。为了铺满整张网格图,我们遍历每个格子,判断能否以当前格子为左上角粘贴邮票,最后,我们检查是否每个空格子都被邮票覆盖即可。关键问题在于:
- 如果快速判断一个矩形范围
(i.j) ~ (x,y)内是否存在被占据的格子。 - 在贴上邮票后如何更新矩阵的状态,并在最后快速判断每个空格子是否被覆盖。
对于第一个问题,我们可以使用二维前缀和解决。定义 sum[i][j] 表示范围 (0,0) ~ (i,j) 内被占据格子的数量,那么对与我们要粘贴邮票的范围 (i.j) ~ (x,y) ,只需判断 sum[x][y]-sum[i-1][y]-sum[x][j-1]+sum[i-1][j-1] 是否为 0 即可。
对于第二个问题,我们可以使用二维差分解决。由于本人之前对于差分的理解不是很到位,所以这里展开说一下。差分可以看作前缀和的逆运算,我们对差分数组求前缀和即可得到原数组,对原数组求前缀和即可得到前缀和数组。假设这里的原数组 arr[i][j] 表示当前格子上的邮票数量,那差分数组 diff 就应该按照下图方式修改:
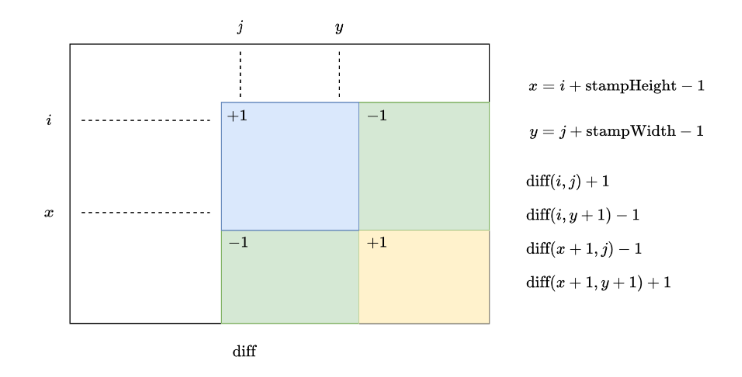
代码
不得不承认,我求二维前缀和、二维差分的代码极其丑陋。。。
class Solution {
public:bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {int m = grid.size(), n = grid[0].size();vector<vector<int>> sum(grid.begin(), grid.end());vector<vector<int>> diff(m, vector<int>(n, 0));for(int i=0;i<m;++i){for(int j=1;j<n;++j){sum[i][j] += sum[i][j-1];}}for(int i=1;i<m;++i){for(int j=0;j<n;++j){sum[i][j] += sum[i-1][j];}}for(int i=0;i<m;++i){for(int j=0;j<n;++j){if(grid[i][j]) continue;int x = i+stampHeight-1, y = j+stampWidth-1;if(x>=m || y>=n) continue;int temp = sum[x][y];if(i>0) temp -= sum[i-1][y];if(j>0) temp -= sum[x][j-1];if(i>0 && j>0) temp += sum[i-1][j-1];if(temp == 0){++diff[i][j];if(x+1<m) --diff[x+1][j];if(y+1<n) --diff[i][y+1];if(x+1<m && y+1<n) ++diff[x+1][y+1];}}}for(int i=0;i<m;++i){for(int j=1;j<n;++j){diff[i][j] += diff[i][j-1];}}for(int i=1;i<m;++i){for(int j=0;j<n;++j){diff[i][j] += diff[i-1][j];}}for(int i=0;i<m;++i){for(int j=0;j<n;++j){if(!grid[i][j] && !diff[i][j]) return false;}}return true;}
};
相关文章:

LeetCode每日一题——2132.用邮票贴满网格图
参考资料: 2132. 用邮票贴满网格图 - 力扣(LeetCode) 题目描述 给你一个 m x n 的二进制矩阵 grid ,每个格子要么为 0 (空)要么为 1 (被占据)。 给你邮票的尺寸为 stampHeight x…...
PyQt6 表单布局Form Layout (QFormLayout)
锋哥原创的PyQt6视频教程: 2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~共计43条视频,包括:2024版 PyQt6 Python桌面开发 视频教程(无废话版…...
函数)
Python: any()函数
在Python中,any函数是一个内置函数,它接受一个可迭代对象作为参数,并返回一个布尔值。当可迭代对象中至少一个元素为真(非零、非空、非None等)时,any函数返回True;否则,返回False。 …...

一些AG10K FPGA 调试的建议-Douglas
PLL AGM FPGA 在配置成功时,PLL 已经完成锁定,lock 信号已经变高;如果原设计中用 lock 信号输出实现系统 reset 的复位功能,就不能正确完成上电复位;同时,为了保证 PLL 相移的稳定,我们需要在 P…...

【模型量化】神经网络量化基础及代码学习总结
1 量化的介绍 量化是减少神经网络计算时间和能耗的最有效的方法之一。在神经网络量化中,权重和激活张量存储在比训练时通常使用的16-bit或32-bit更低的比特精度。当从32-bit降低到8-bit,存储张量的内存开销减少了4倍,矩阵乘法的计算成本则二…...

次模和K次模是多项式可解吗?
次模是多项式可解吗 **是的,**次模函数的最优化问题通常是多项式时间可解的。这是因为次模性质导致了问题的结构,使得可以利用高效的算法进行求解。 具体来说,针对次模函数的最优化问题,例如极大化或极小化这样的目标函数…...
网络安全——SQL注入实验
一、实验目的要求: 二、实验设备与环境: 三、实验原理: 四、实验步骤: 五、实验现象、结果记录及整理: 六、分析讨论与思考题解答: 七、实验截图: 一、实验目的要求: 1、…...

【cocotb】【达坦科技DatenLord】Cocotb Workshop分享
https://www.bilibili.com/video/BV19e4y1k7EE/?spm_id_from333.337.search-card.all.click&vd_sourcefd0f4be6d0a5aaa0a79d89604df3154a 方便RFM实现 cocotb_test 替代makefile , 类似python 函数执行...

Kafka系列之:统计kafka集群Topic的分区数和副本数,批量增加topic副本数
Kafka系列之:统计kafka集群Topic的分区数和副本数,批量增加topic副本数 一、创建KafkaAdminClient二、获取kafka集群topic元信息三、获取每个topic的名称、分区数、副本数四、生成增加topic副本的json文件五、执行增加topic副本的命令六、确认topic增加副本是否成功一、创建K…...

开具实习证明:在线实习项目介绍
大数据在线实习项目,是在线上为学生提供实习经验的项目。我们希望能够帮助想要在毕业后从事数据科学类工作的学生更加顺利地适应从教室到职场的转换;也帮助那些在工作中需要处理数据、实现数据价值的其他职能的从业者高效快速地掌握每天都能用起来的数据…...
MFC逆向之CrackMe Level3 过反调试 + 写注册机
今天我来分享一下,过反调试的方法以及使用IDA还原代码 写注册机的过程 由于内容太多,我准备分为两个帖子写,这个帖子主要是写IDA还原代码,下一个帖子是写反调试的分析以及过反调试和异常 这个CrackMe Level3是一个朋友发我的,我也不知道他在哪里弄的,我感觉挺好玩的,对反调试…...

【Centos】
一、Virtualbox安装Centos 1、Virtualbox 下载地址: Virtualbox 2、Centos 下载地址: Centos 3、Virtualbox安装Centos教程 Virtualbox安装Centos教程: Virtualbox安装Centos教程...

1+X大数据平台运维职业技能等级证书中级
hadoop: 由于我的功能限制,我无法直接为您执行这些操作或提供实际的截图。但我可以为您提供一步步的指导,帮助您完成这些任务。 1. 解压JDK安装包到“/usr/local/src”路径,并配置环境变量。 - 解压JDK:tar -zxf jd…...
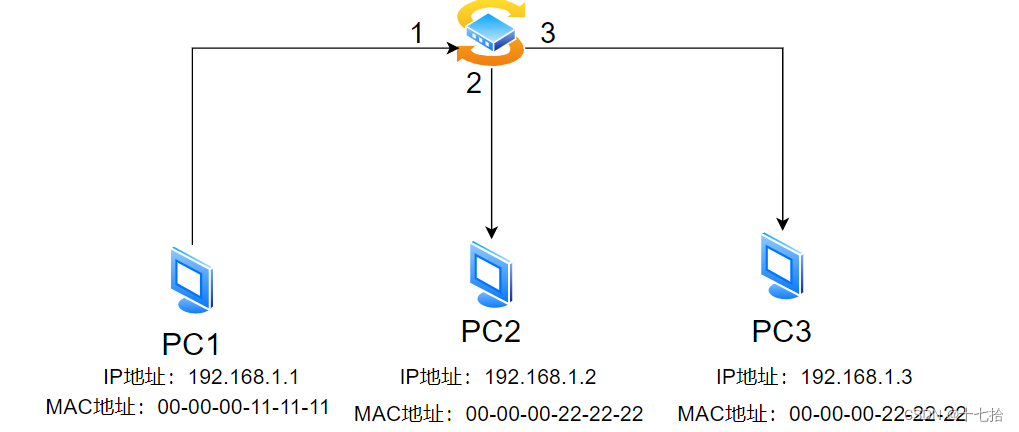
网络基础(五):网络层协议介绍
目录 一、网络层 1、网络层的概念 2、网络层功能 3、IP数据包格式 二、ICMP协议 1、ICMP的作用和功能 2、ping命令的使用 2.1ping命令的通用格式 2.2ping命令的常用参数 2.3TypeCode:查看不同功能的ICMP报文 2.4ping出现问题 3、Tracert 4、冲突域 5、…...
浅显易懂 @JsonIgnore 的作用
1.JsonIgnore作用 在json序列化/反序列化时将java bean中使用了该注解的属性忽略掉 2.这个注解可以用在类/属性上 例如:在返回user对象时,在pwd属性上使用这个注解,返回user对象时会直接去掉pwd这个字段,不管这个属性有没…...

【计算机设计大赛作品】诗意千年—唐朝诗人群像的数字展现_附源码—信息可视化赛道获奖项目深入剖析【可视化项目案例-20】
🎉🎊🎉 你的技术旅程将在这里启航! 记得看本专栏里顶置的可视化宝典导航贴哦! 🚀🚀 本专栏为可视化专栏,包含现有的所有可视化技术。订阅专栏用户在文章底部可下载对应案例完整源码以供大家深入的学习研究。 🎓 每一个案例都会提供完整代码和详细的讲解,不论你…...
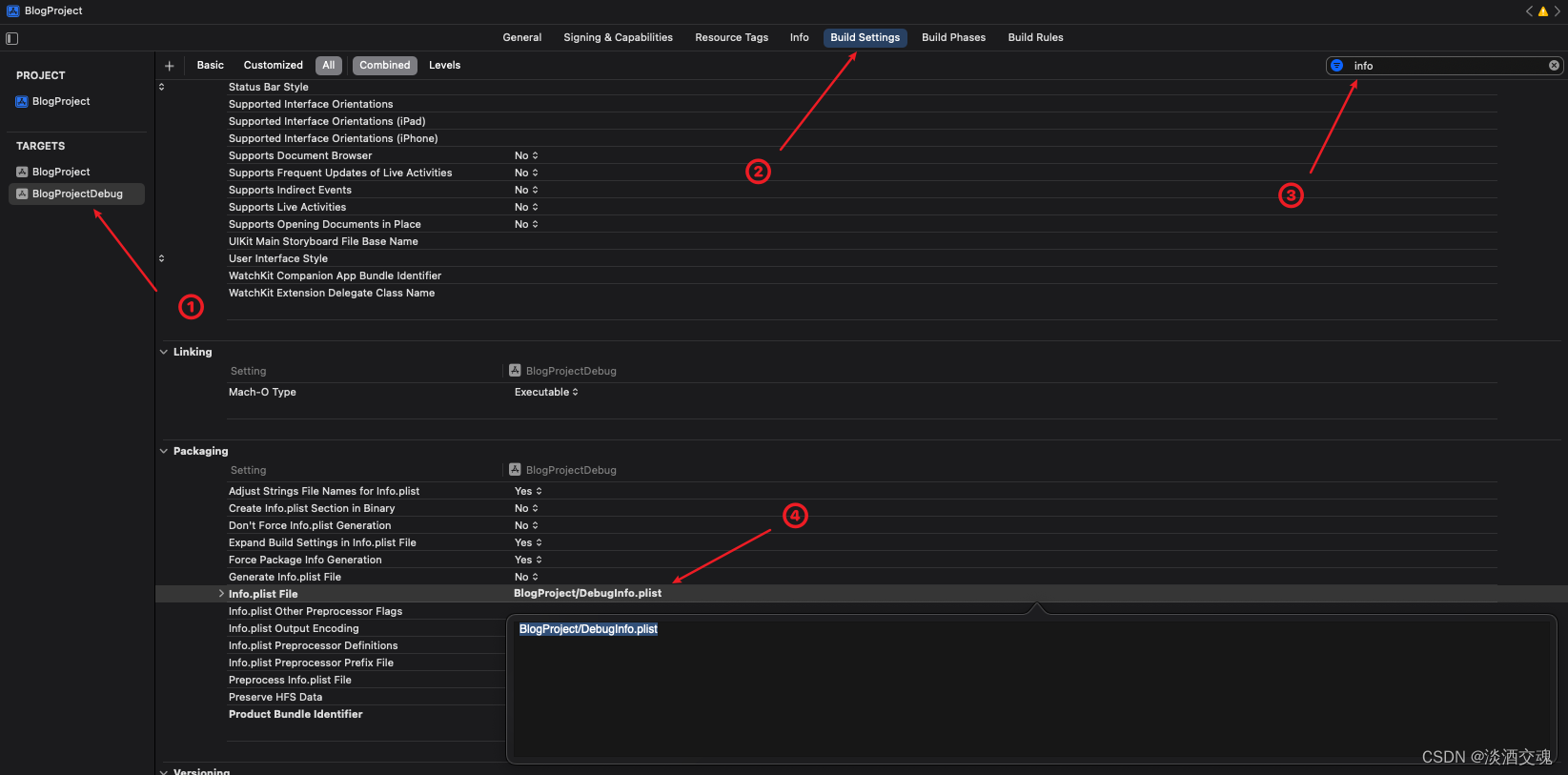
「Swift」Xcode多Target创建
前言:我们日常开发中会使用多个环境,如Dev、UAT,每个环境对应的业务功能都不同,但每个环境之间都只存在较小的差异,所以此时可以使用创建多个Target来实现,每个Target对应这个一个App,可以实现一…...

Python文件命名规则:批量重命名与规则匹配的文件
我从一个旧的 iOS 项目中获得了一个文件夹,其中包含许多类似于 image.png image2x.png another-image.png another-image2x.png然而,由于该项目现在只需要 2x.png 图像,我已经删除了所有的文件没有 2x 的名称。 但是我现在想知道如何轻松…...

『npm』一条命令快速配置npm淘宝国内镜像
📣读完这篇文章里你能收获到 一条命令快速切换至淘宝镜像恢复官方镜像 文章目录 一、设置淘宝镜像源二、恢复官方镜像源三、查看当前使用的镜像 一、设置淘宝镜像源 npm config set registry https://registry.npm.taobao.org服务器建议全局设置 sudo npm config…...
Java EE 多线程之线程安全的集合类
文章目录 1. 多线程环境使用 ArrayList1. 1 Collections.synchronizedList(new ArrayList)1.2 CopyOnWriteArrayList 2. 多线程环境使用队列2.1 ArrayBlockingQueue2.2 LinkedBlockingQueue2.3 PriorityBlockingQueue2.4 TransferQueue 3. 多线程环境使用哈希表3.1 Hashtable3.…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
