除法求值[中等]
一、题目
给你一个变量对数组equations和一个实数值数组values作为已知条件,其中equations[i] = [Ai, Bi]和values[i]共同表示等式Ai / Bi = values[i]。每个Ai或Bi是一个表示单个变量的字符串。另有一些以数组queries表示的问题,其中queries[j] = [Cj, Dj]表示第j个问题,请你根据已知条件找出Cj / Dj = ?的结果作为答案。返回 所有问题的答案 。如果存在某个无法确定的答案,则用-1.0替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用-1.0替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为0的情况,且不存在任何矛盾的结果。
注意:未在等式列表中出现的变量是未定义的,因此无法确定它们的答案。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意:x是未定义的=> -1.0
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
1 <= equations.length <= 20
equations[i].length == 2
1 <= Ai.length, Bi.length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= Cj.length, Dj.length <= 5
Ai,Bi,Cj,Dj由小写英文字母与数字组成
二、代码
广度优先搜索: 我们可以将整个问题建模成一张图:给定图中的一些点(变量),以及某些边的权值(两个变量的比值),试对任意两点(两个变量)求出其路径长(两个变量的比值)。因此,我们首先需要遍历equations数组,找出其中所有不同的字符串,并通过哈希表将每个不同的字符串映射成整数。
在构建完图之后,对于任何一个查询,就可以从起点出发,通过广度优先搜索的方式,不断更新起点与当前点之间的路径长度,直到搜索到终点为止。
class Solution {public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {int nvars = 0;Map<String, Integer> variables = new HashMap<String, Integer>();int n = equations.size();for (int i = 0; i < n; i++) {if (!variables.containsKey(equations.get(i).get(0))) {variables.put(equations.get(i).get(0), nvars++);}if (!variables.containsKey(equations.get(i).get(1))) {variables.put(equations.get(i).get(1), nvars++);}}// 对于每个点,存储其直接连接到的所有点及对应的权值List<Pair>[] edges = new List[nvars];for (int i = 0; i < nvars; i++) {edges[i] = new ArrayList<Pair>();}for (int i = 0; i < n; i++) {int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));edges[va].add(new Pair(vb, values[i]));edges[vb].add(new Pair(va, 1.0 / values[i]));}int queriesCount = queries.size();double[] ret = new double[queriesCount];for (int i = 0; i < queriesCount; i++) {List<String> query = queries.get(i);double result = -1.0;if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));if (ia == ib) {result = 1.0;} else {Queue<Integer> points = new LinkedList<Integer>();points.offer(ia);double[] ratios = new double[nvars];Arrays.fill(ratios, -1.0);ratios[ia] = 1.0;while (!points.isEmpty() && ratios[ib] < 0) {int x = points.poll();for (Pair pair : edges[x]) {int y = pair.index;double val = pair.value;if (ratios[y] < 0) {ratios[y] = ratios[x] * val;points.offer(y);}}}result = ratios[ib];}}ret[i] = result;}return ret;}
}class Pair {int index;double value;Pair(int index, double value) {this.index = index;this.value = value;}
}
时间复杂度: O(ML+Q⋅(L+M)),其中M为边的数量,Q为询问的数量,L为字符串的平均长度。构建图时,需要处理M条边,每条边都涉及到O(L)的字符串比较;处理查询时,每次查询首先要进行一次O(L)的比较,然后至多遍历O(M)条边。
空间复杂度: O(NL+M),其中N为点的数量,M为边的数量,L为字符串的平均长度。为了将每个字符串映射到整数,需要开辟空间为O(NL)的哈希表;随后,需要花费O(M)的空间存储每条边的权重;处理查询时,还需要O(N)的空间维护访问队列。最终,总的复杂度为O(NL+M+N)=O(NL+M)。
【2】Floyd 算法: 对于查询数量很多的情形,如果为每次查询都独立搜索一次,则效率会变低。为此,我们不妨对图先做一定的预处理,随后就可以在较短的时间内回答每个查询。在本题中,我们可以使用Floyd算法,预先计算出任意两点之间的距离。
class Solution {public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {int nvars = 0;Map<String, Integer> variables = new HashMap<String, Integer>();int n = equations.size();for (int i = 0; i < n; i++) {if (!variables.containsKey(equations.get(i).get(0))) {variables.put(equations.get(i).get(0), nvars++);}if (!variables.containsKey(equations.get(i).get(1))) {variables.put(equations.get(i).get(1), nvars++);}}double[][] graph = new double[nvars][nvars];for (int i = 0; i < nvars; i++) {Arrays.fill(graph[i], -1.0);}for (int i = 0; i < n; i++) {int va = variables.get(equations.get(i).get(0)), vb = variables.get(equations.get(i).get(1));graph[va][vb] = values[i];graph[vb][va] = 1.0 / values[i];}for (int k = 0; k < nvars; k++) {for (int i = 0; i < nvars; i++) {for (int j = 0; j < nvars; j++) {if (graph[i][k] > 0 && graph[k][j] > 0) {graph[i][j] = graph[i][k] * graph[k][j];}}}}int queriesCount = queries.size();double[] ret = new double[queriesCount];for (int i = 0; i < queriesCount; i++) {List<String> query = queries.get(i);double result = -1.0;if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {int ia = variables.get(query.get(0)), ib = variables.get(query.get(1));if (graph[ia][ib] > 0) {result = graph[ia][ib];}}ret[i] = result;}return ret;}
}
时间复杂度: O(ML+N3+QL)。构建图需要O(ML)的时间;Floyd算法需要O(N^3)的时间;处理查询时,单次查询只需要O(L)的字符串比较以及常数时间的额外操作。
空间复杂度: O(NL+N^2)。
相关文章:

除法求值[中等]
一、题目 给你一个变量对数组equations和一个实数值数组values作为已知条件,其中equations[i] [Ai, Bi]和values[i]共同表示等式Ai / Bi values[i]。每个Ai或Bi是一个表示单个变量的字符串。另有一些以数组queries表示的问题,其中queries[j] [Cj, Dj…...

新时代商业市场:AR技术的挑战与机遇并存
随着科技的不断发展,增强现实(AR)技术逐渐成为当今社会的一个重要组成部分。AR技术能够将虚拟世界与现实世界相结合,为人们提供更加丰富、多样化的体验。在新时代的社会商业市场中,AR技术也正逐渐被应用于各种商业活动…...

RHEL8中ansible的使用
编写ansible.cfg和清单文件ansible的基本用法 本章实验三台RHEL8系统(rhel801,rhel802,rhel803),其中rhel801是ansible主机 这里要确保ansible主机能够解析所有被管理的机器,这里通过配置/etc/hosts来实现…...

【1.6计算机组成与体系结构】存储系统
目录 1.层次化存储结构2.Cache2.1 Cache的介绍2.2 局部性原理2.3 Cache应用 1.层次化存储结构 由 ⬆ CPU:寄存器。 快 ⬆ Cache:按内容存取(相联存储器)。 到 ⬆内存(主存):DRAM。 慢 ⬆ 外存(辅存&#…...
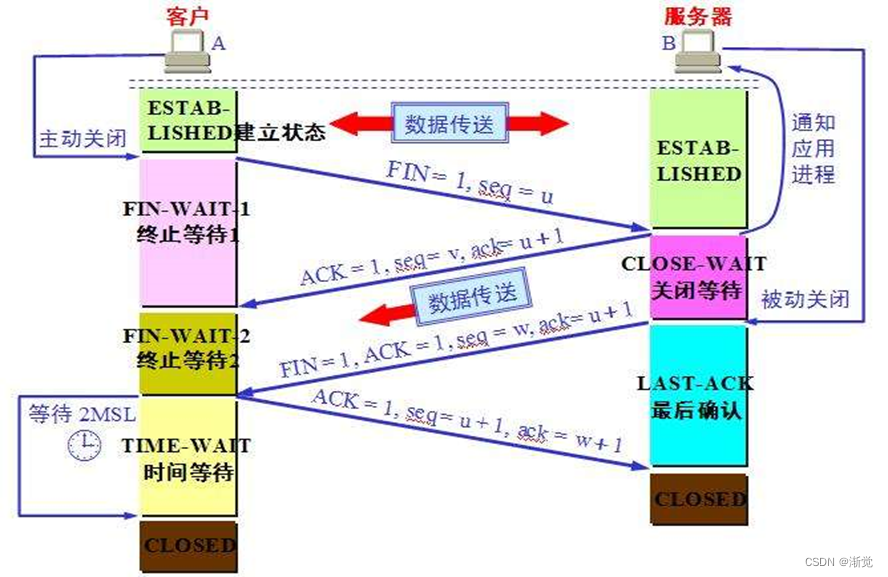
TCP/UDP 协议
目录 一.TCP协议 1.介绍 2.报文格式 编辑 确认号 控制位 窗口大小 3.TCP特性 二.TCP协议的三次握手 1.tcp 三次握手的过程 三.四次挥手 2.有限状态机 四.tcp协议和udp协议的区别 五.udp协议 UDP特性 六.telnet协议 一.TCP协议 1.介绍 TCP(Transm…...

如何正确理解和使用 Golang 中 nil ?
目录 指针中的 nil 切片中的 nil map 中的 nil 通道中的 nil 函数中的 nil 接口中的 nil 避免 nil 相关问题的最佳实践 小结 在 Golang 中,nil 是一个预定义的标识符,在不同的上下文环境中有不同的含义,但通常表示“无”、“空”或“…...
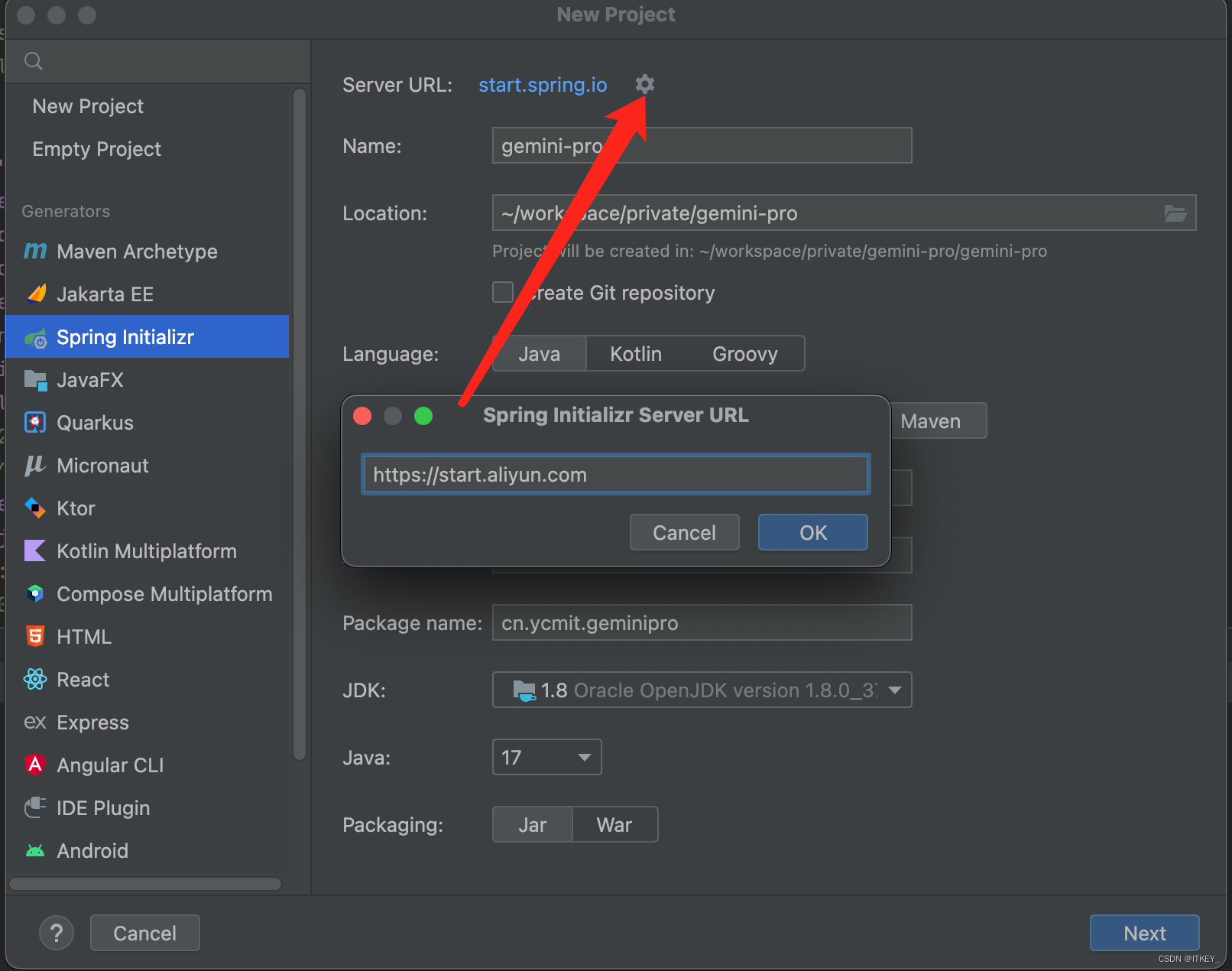
IDEA新建jdk8 spring boot项目
今天新建spring boot项目发现JDK版本最低可选17。 但是目前用的最多的还是JDK8啊。 解决办法 Server URL中设置: https://start.aliyun.com/设置完成后,又可以愉快的用jdk8创建项目了。 参考 https://blog.csdn.net/imbzz/article/details/13469117…...

Qt/C++音视频开发59-使用mdk-sdk组件/原qtav作者力作/性能凶残/超级跨平台
一、前言 最近一个月一直在研究mdk-sdk音视频组件,这个组件是原qtav作者的最新力作,提供了各种各样的示例demo,不仅限于支持C,其他各种比如java/flutter/web/android等全部支持,性能上也是杠杠的,目前大概…...

智安网络|企业网络安全工具对比:云桌面与堡垒机,哪个更适合您的需求
随着云计算技术的快速发展,越来越多的企业开始采用云计算解决方案来提高效率和灵活性。在云计算环境下,云桌面和堡垒机被广泛应用于企业网络安全和办公环境中。尽管它们都有助于提升企业的安全和效率,但云桌面和堡垒机在功能和应用方面存在着…...
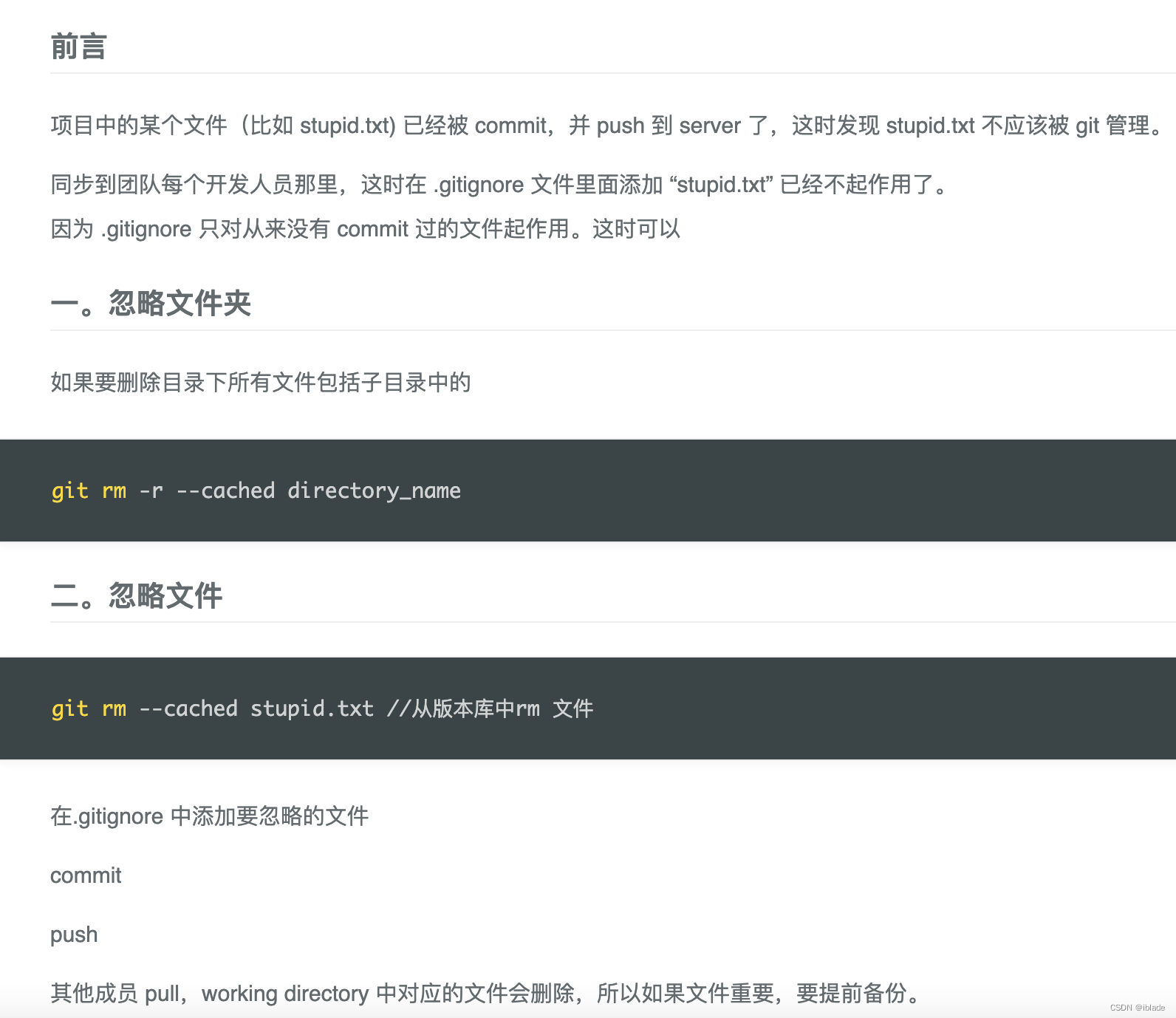
Git忽略已经提交的文件
原理类似于 Android修改submodule的lib包名...

MVVM和MVC以及MVP的原理以及它们的区别
MVVM、MVC 和 MVP 都是前端架构模式,它们各自有不同的原理和特点。 MVC(Model-View-Controller) 原理:MVC 将应用程序分为三个部分:模型(Model)、视图(View)和控制器&a…...
WeChatMsg: 导出微信聊天记录 | 开源日报 No.108
Mozilla-Ocho/llamafile Stars: 3.5k License: NOASSERTION llamafile 是一个开源项目,旨在通过将 lama.cpp 与 Cosmopolitan Libc 结合成一个框架,将 LLM (Large Language Models) 的复杂性折叠到单个文件可执行程序中,并使其能够在大多数…...
)
Python学习之复习MySQL-Day3(DQL)
目录 文章声明⭐⭐⭐让我们开始今天的学习吧!DQL简介基本查询查询多个/全部字段设置别名去除重复记录 条件查询条件查询介绍实例演示 聚合函数什么是聚合函数?常见的聚合函数实例演示 分组查询分组查询语法where 和 having 的区别实例演示 排序查询语法实…...

AI超级个体:ChatGPT与AIGC实战指南
目录 前言 一、ChatGPT在日常工作中的应用场景 1. 客户服务与支持 2. 内部沟通与协作 3. 创新与问题解决 二、巧用ChatGPT提升工作效率 1. 自动化工作流程 2. 信息整合与共享 3. 提高决策效率 三、巧用ChatGPT创造价值 1. 优化产品和服务 2. 提高员工满意度和留任率…...
|(使用OkHttpClient实现websocket以及详细介绍))
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)
SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍) 文章目录 SpringBoot集成websocket(5)|(使用OkHttpClient实现websocket以及详细介绍)[TOC] 前言一、初始…...
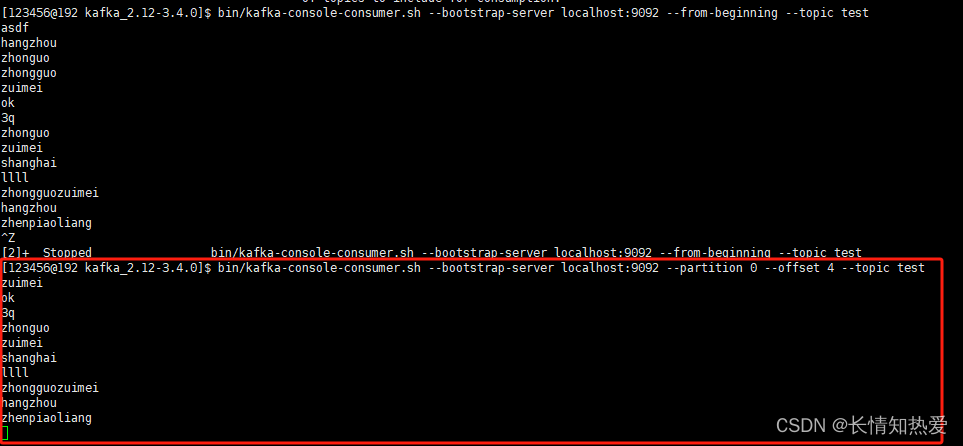
Kafka-Kafka基本原理与集群快速搭建(实践)
Kafka单机搭建 下载Kafka Apache Download Mirrors 解压 tar -zxvf kafka_2.12-3.4.0.tgz -C /usr/local/src/software/kafkakafka内部bin目录下有个内置的zookeeper(用于单机) 启动zookeeper(在后台启动) nohup bin/zookeeper-server-start.sh conf…...
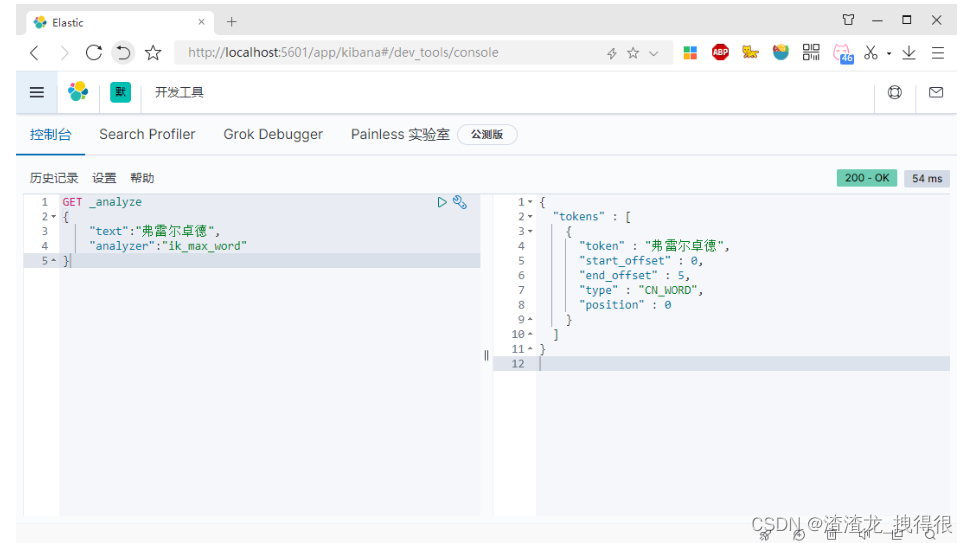
Elasticsearch 进阶(索引、类型、字段、分片、副本、集群等详细说明)-06
笔记来源:Elasticsearch Elasticsearch进阶 进阶-核心概念 索引Index 一个索引就是一个拥有几分相似特征的文档的集合。比如说,你可以有一个客户数据的索引,另一个产品目录的索引,还有一个订单数据的索引。一个索引由一个名字…...
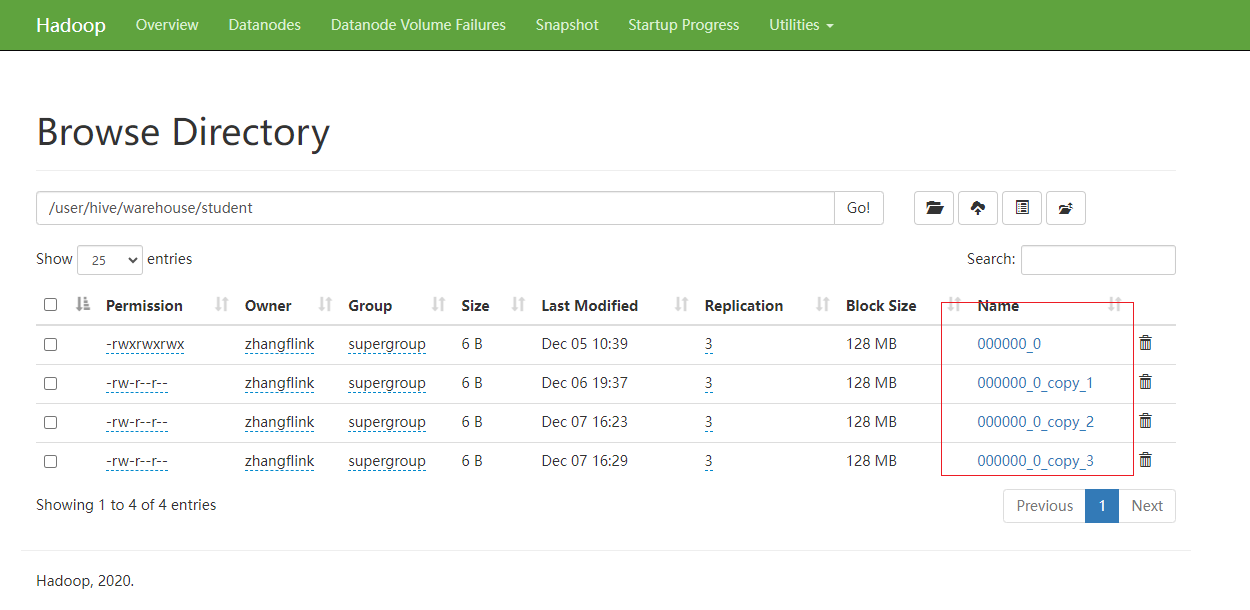
hive的分区表和分桶表详解
分区表 Hive中的分区就是把一张大表的数据按照业务需要分散的存储到多个目录,每个目录就称为该表的一个分区。在查询时通过where子句中的表达式选择查询所需要的分区,这样的查询效率会提高很多。 静态分区表基本语法 创建分区表 create table dept_p…...
verilog语法进阶-分布式ram
概述: FPGA的LUT查找表是用RAM设计的,所以LUT可以当成ram来使用,也并不是所有的LUT都可以当成ram来使用,sliceM的ram可以当成分布式ram来使用,而sliceL的ram只能当成rom来使用,也就是只能读,不能写&#x…...

HarmonyOS使用HTTP访问网络
HTTP数据请求 1 概述 日常生活中我们使用应用程序看新闻、发送消息等,都需要连接到互联网,从服务端获取数据。例如,新闻应用可以从新闻服务器中获取最新的热点新闻,从而给用户打造更加丰富、更加实用的体验。 那么要实现这样一种…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
