逻辑回归代价函数
逻辑回归的代价函数通常使用交叉熵损失来定义。这种损失函数非常适合于二元分类问题。
本篇来推导一下逻辑回归的代价函数。
首先,我们在之前了解了逻辑回归的定义:逻辑回归模型是一种用于二元分类的模型,其预测值是一个介于0和1之间的概率。模型的形式是一个S形的逻辑函数(sigmoid函数),但是sigmoid函数的参数到底要选哪个,就需要对sigmoid函数的结果进行评判,因此也就需要第二步:损失评估。
举个例子:
假设我们有一个逻辑回归模型,用来预测学生是否会通过最终考试。我们有两个特征:学生的出勤率和平均成绩。模型的目标是基于这些特征预测学生是否会通过考试("通过"记为1,"不通过"记为0)。
特征和参数
- 假设特征向量 x = [ x 1 x 2 ] x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} x=[x1x2],其中 x 1 x_1 x1是学生的出勤率, x 2 x_2 x2是学生的平均成绩。
- 模型的参数为 θ = [ θ 0 θ 1 θ 2 ] \theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix} θ= θ0θ1θ2 ,其中 θ 0 \theta_0 θ0是偏置项, θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2分别是与出勤率和平均成绩相关的权重。
计算 h ( x ) h(x) h(x)
模型会计算 h ( x ) h(x) h(x),即给定特征时通过考试的预测概率。这是通过sigmoid函数来完成的:
h θ ( x ) = 1 1 + e − ( θ 0 + θ 1 x 1 + θ 2 x 2 ) h_\theta(x) = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2)}} hθ(x)=1+e−(θ0+θ1x1+θ2x2)1
假设对于一个特定学生,出勤率 x 1 = 0.85 x_1 = 0.85 x1=0.85(85%),平均成绩 x 2 = 75 x_2 = 75 x2=75,而模型参数为 θ 0 = − 4 \theta_0 = -4 θ0=−4, θ 1 = 10 \theta_1 = 10 θ1=10, θ 2 = 0.05 \theta_2 = 0.05 θ2=0.05。那么 h ( x ) h(x) h(x)的计算为:
h θ ( x ) = 1 1 + e − ( − 4 + 10 × 0.85 + 0.05 × 75 ) h_\theta(x) = \frac{1}{1 + e^{-(-4 + 10 \times 0.85 + 0.05 \times 75)}} hθ(x)=1+e−(−4+10×0.85+0.05×75)1
计算这个表达式的值(这需要一些数学运算),假设结果是 h θ ( x ) ≈ 0.76 h_\theta(x) \approx 0.76 hθ(x)≈0.76。这意味着根据我们的模型,这个学生通过考试的预测概率是 76%。基于这个预测,由于概率大于0.5,我们可以预测这个学生会通过考试。
到这一步为止, θ 0 = − 4 \theta_0 = -4 θ0=−4, θ 1 = 10 \theta_1 = 10 θ1=10, θ 2 = 0.05 \theta_2 = 0.05 θ2=0.05实际上是我们随机(或经验)取的一组参数数值,但其并不是最佳的,所以就需要有一个代价函数来判断整体的损失(正确率),再进行梯度下降(或其他优化算法)来迭代地调整这些参数,以获得最小化损失。
在逻辑回归中,由于目标结果只有0和1两种情况,因此去计算一组数据的损失的时候就需要区分成两个函数:
当 y=1 时的损失函数
Cost when y = 1 : − log ( h θ ( x ) ) \text{Cost when } y = 1: -\log(h_\theta(x)) Cost when y=1:−log(hθ(x))
当 y=0 时的损失函数
Cost when y = 0 : − log ( 1 − h θ ( x ) ) \text{Cost when } y = 0: -\log(1 - h_\theta(x)) Cost when y=0:−log(1−hθ(x))
对应的图如下:
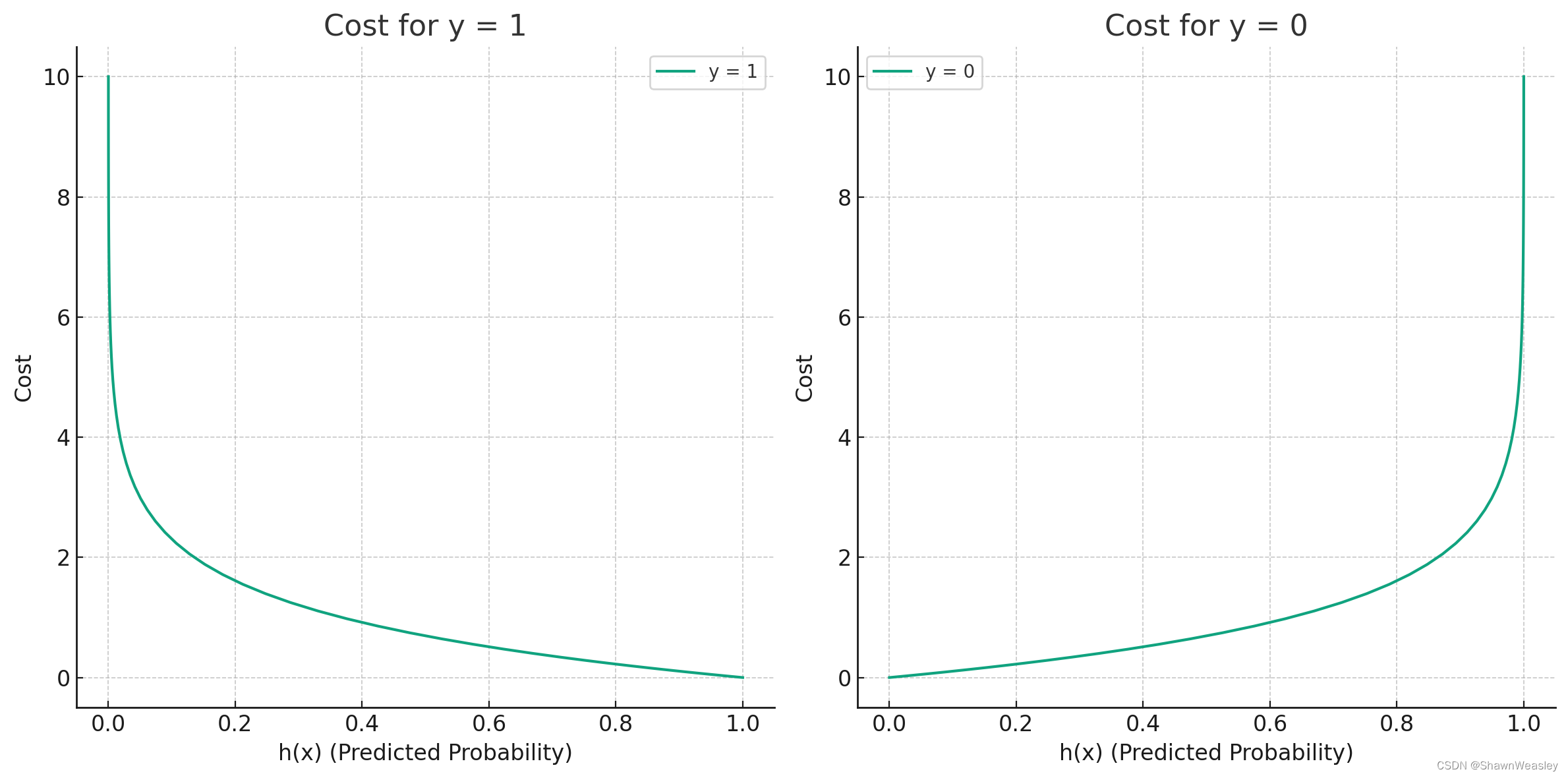
用一个式子来同时包含这两个情况就是我们的逻辑回归的代价函数(交叉熵损失):
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
我们可以看到这里 l o g ( h θ ( x ( i ) ) ) log(h_\theta(x^{(i)})) log(hθ(x(i)))前面乘以了 y ( i ) y^{(i)} y(i),所以当目标值为0的时候,这部分就变成了0,也就不会影响后面部分的计算,就很简单地实现了两个式子融合。
相关文章:

逻辑回归代价函数
逻辑回归的代价函数通常使用交叉熵损失来定义。这种损失函数非常适合于二元分类问题。 本篇来推导一下逻辑回归的代价函数。 首先,我们在之前了解了逻辑回归的定义:逻辑回归模型是一种用于二元分类的模型,其预测值是一个介于0和1之间的概率…...

芯知识 | WT2003Hx系列高品质语音芯片MP3音频解码IC的特征与应用优势
在嵌入式语音领域,唯创知音WT2003Hx系列高品质语音芯片以其卓越的音频解码性能脱颖而出。本文将深入研究该系列芯片的特色与应用优势,重点关注其支持wav、Mp3格式音频解码、高品质播放等方面。 特色一:支持wav、Mp3格式音频解码 1.多格式兼…...

node.js 启一个前端代理服务
文章目录 前言一、分析技术二、操作步骤2.1、下载依赖2.2、创建一个 serve.js 文件2.3、js 文件中写入以下代码 三、运行: node serve四、结果展示五、总结六、感谢 前言 有时候我们需要做一些基础的页面时,在研发过程中需要代理调用接口避免浏览器跨域…...

弹性搜索引擎Elasticsearch:本地部署与远程访问指南
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、Cpolar杂谈 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言系统环境1. Windows 安装Elasticsearch2. 本地访问Elasticsearch3. Windows 安装…...

微信小程序生成二维码海报并分享
背景:点击图标,生成海报后,点击保存相册,可以保存 生成海报:插件wxa-plugin-canvas,此处使用页面异步生成组件方式,官网地址:wxa-plugin-canvas - npm 二维码:调用后端…...
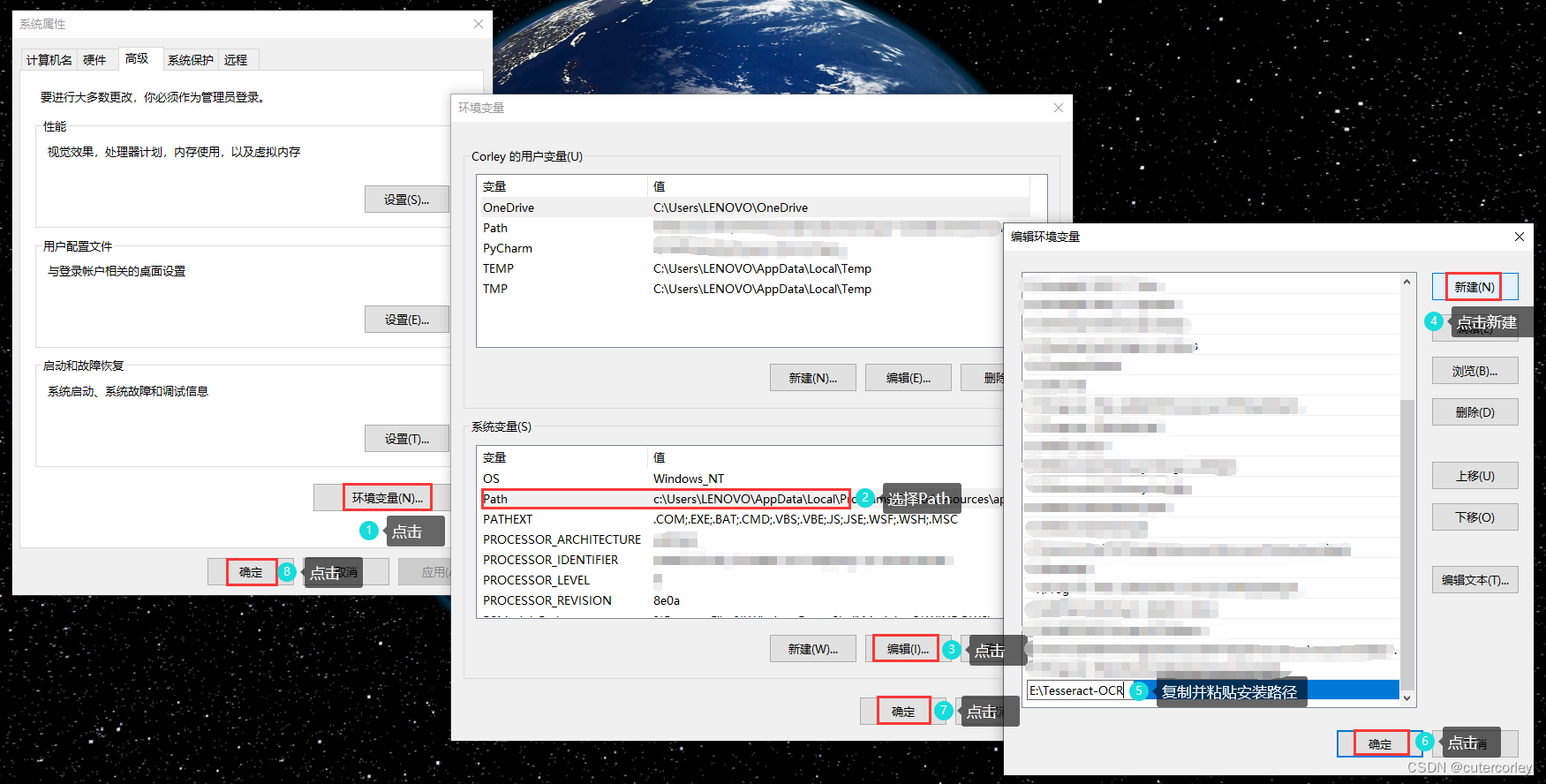
Windows安装Tesseract OCR与Python中使用pytesseract进行文字识别
文章目录 前言一、下载并安装Tesseract OCR二、配置环境变量三、Python中安装使用pytesseract总结 前言 Tesseract OCR是一个开源OCR(Optical Character Recognition)引擎,用于从图像中提取文本。Pytesseract是Tesseract OCR的Python封装&am…...
【答案】2023年国赛信息安全管理与评估第三阶段夺旗挑战CTF(网络安全渗透)
【答案】2023年国赛信息安全管理与评估第三阶段夺旗挑战CTF(网络安全渗透) 全国职业院校技能大赛高职组信息安全管理与评估 (赛项) 评分标准 第三阶段 夺旗挑战CTF(网络安全渗透) *竞赛项目赛题* 本文…...
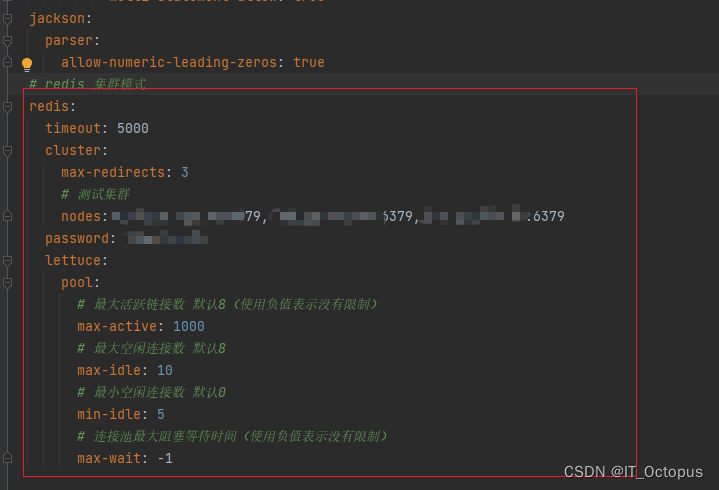
springboot 集成 redis luttuce redisson ,单机 集群模式(根据不同环境读取不同环境的配置)
luttuce 和redisson配置过程中实际上是独立的,他们两个可以同时集成,但是没有直接相关关系,配置相对独立。 所以分为Lettuce 和 Redisson 两套配置 父pom <!-- Spring Data Redis --><dependency><groupId>org.springframe…...
PPT插件-好用的插件-PPT 素材该怎么积累-大珩助手
PPT 素材该怎么积累? 使用大珩助手中的素材库功能,将Word中的,或系统中的文本文件、图片、其他word文档、pdf,所有见到的好素材,一键收纳。 步骤:选中文件,按住鼠标左键拖到素材库界面中&…...

qt 正则表达式简单介绍
正则表达式即一个文本匹配字符串的一种模式,Qt中使用QRegExp类进行模式匹配.主要应用:字符串验证,搜索,替换,分割..... 正则表达式中字符及字符集 c 匹配字符本身,如a匹配a \c 跟在\后面的字符匹配字符本身,但本表中下面指定的这些字符除外。 \a 匹…...
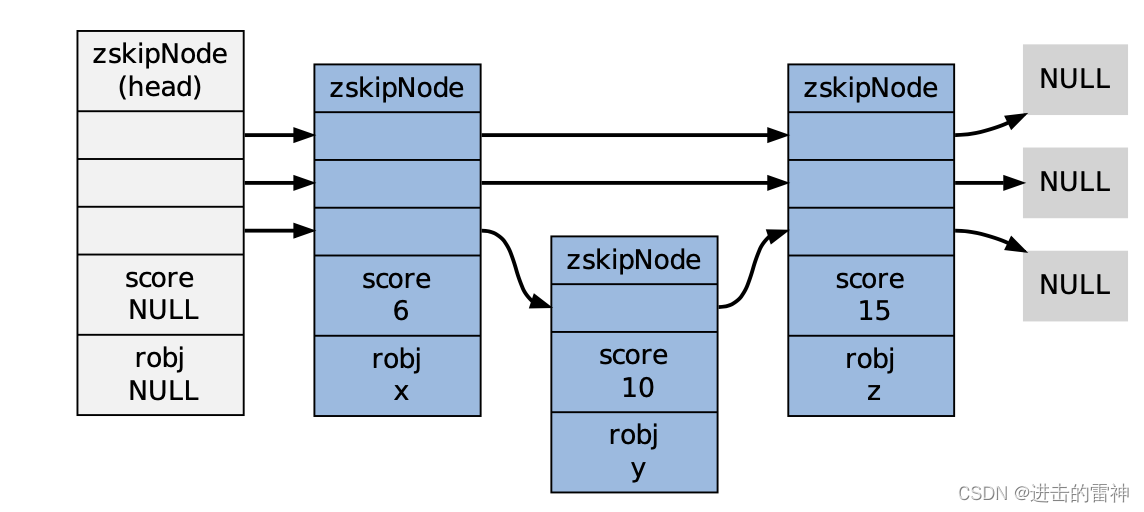
Redis设计与实现之跳跃表
目录 一、跳跃表 1、跳跃表的实现 2、跳跃表的应用 3、跳跃表的时间复杂度是什么? 二、跳跃表有哪些应用场景? 三、跳跃表和其他数据结构(如数组、链表等)相比有什么优点和缺点? 四、Redis的跳跃表支持并发操作吗…...

[每周一更]-(第27期):HTTP压测工具之wrk
[补充完善往期内容] wrk是一款简单的HTTP压测工具,托管在Github上,https://github.com/wg/wrkwrk 的一个很好的特性就是能用很少的线程压出很大的并发量. 原因是它使用了一些操作系统特定的高性能 io 机制, 比如 select, epoll, kqueue 等. 其实它是复用了 redis 的 ae 异步事…...
【FunASR】Paraformer语音识别-中文-通用-16k-离线-large-onnx
模型亮点 模型文件: damo/speech_paraformer-large-vad-punc_asr_nat-zh-cn-16k-common-vocab8404-pytorchParaformer-large长音频模型集成VAD、ASR、标点与时间戳功能,可直接对时长为数小时音频进行识别,并输出带标点文字与时间戳: ASR模型…...

C语言中的柔性数组
uint8_t data[0];代码的含义老虎开始对这个数组不太了解,查阅后得知这是个柔性数组。 C语言中的柔性数组(Flexible Array Member)是一种特殊的数组,它被定义在结构体的最后一个元素中,其大小未知,也就是所…...

ca-certificates.crt解析加载到nssdb中
openssl crl2pkcs7 -nocrl -certfile /etc/ssl/certs/ca-certificates.crt | openssl pkcs7 -print_certs -noout -text ca-certificates.crt为操作系统根证书列表。 获取证书以后使用PK11_ImportDERCert将证书导入到nssdb中 base::FilePath cert_path base::FilePath("…...
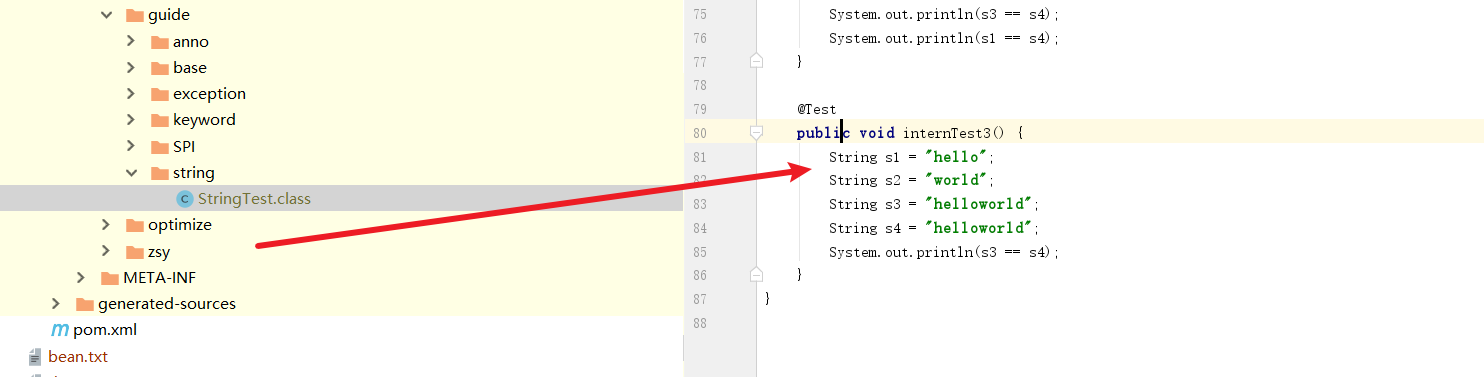
聊聊Java中的常用类String
String、StringBuffer、StringBuilder 的区别 从可变性分析 String不可变。StringBuffer、StringBuilder都继承自AbstractStringBuilder ,两者的底层的数组value并没有使用private和final修饰,所以是可变的。 AbstractStringBuilder 源码如下所示 ab…...

R语言piecewiseSEM结构方程模型在生态环境领域实践技术
结构方程模型(Sructural Equation Modeling,SEM)可分析系统内变量间的相互关系,并通过图形化方式清晰展示系统中多变量因果关系网,具有强大的数据分析功能和广泛的适用性,是近年来生态、进化、环境、地学、…...
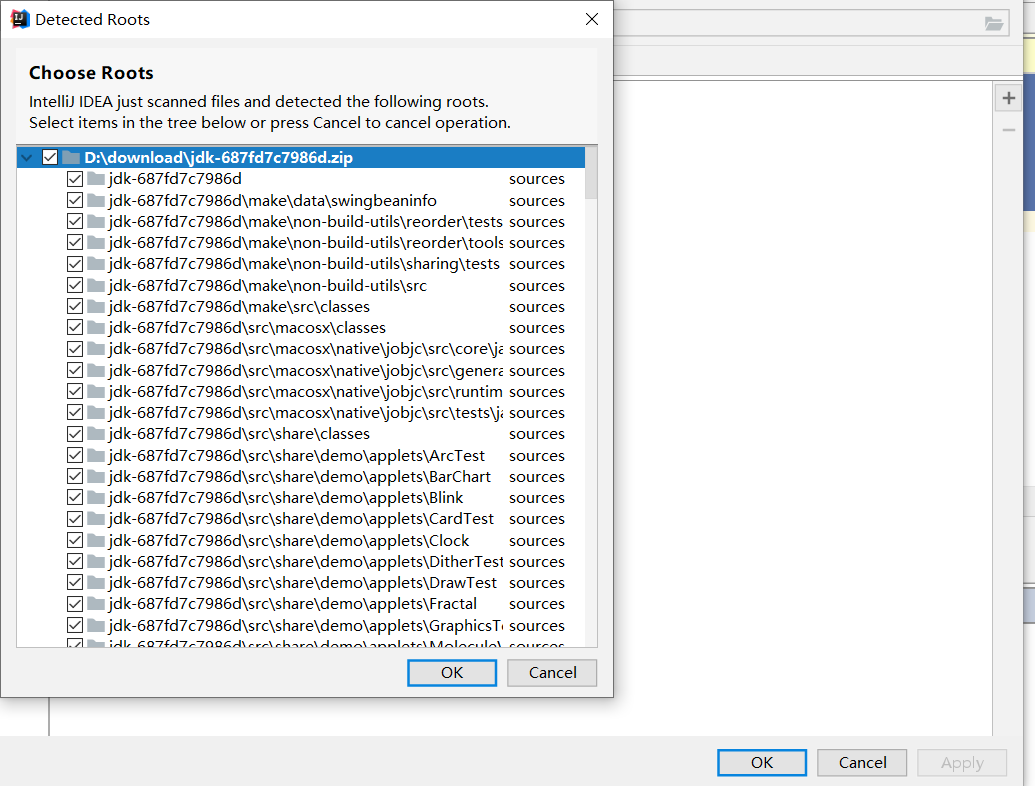
IDEA设置查看JDK源码
问题 我们在查看JDK源码时,可能会遇到这种情况,步入底层查看JDK源码时,出现一堆var变量,可读性非常之差,例如笔者最近想看到nio包下的SocketChannelImpl的write方法,结果看到这样一番景象: pu…...

SSM—Mybatis
目录 和其它持久化层技术对比 搭建MyBatis 开发环境 创建maven工程 创建MyBatis的核心配置文件 创建mapper接口 创建MyBatis的映射文件 通过junit测试功能 加入log4j日志功能 核心配置文件详解 MyBatis的增删改查 新增 删除 修改 查询一个实体类对象 查询list集…...

MYSQL在不删除数据的情况下,重置主键自增id
MYSQL在不删除数据的情况下,重置主键自增id 方法一: SET num : 0; UPDATE table_name SET id num : (num1); ALTER TABLE table_name AUTO_INCREMENT 1; 方法二: 背景(mysql 数据在进行多次删除新增之后id变得很大,但是并没…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
