机器学习-KL散度的直观理解+代码
KL散度
直观理解:
KL散度是一种衡量两个分布之间匹配程度的方法。通常在概率和统计中,我们会用更简单的近似分布来代替观察到的数据或复杂的分布,KL散度帮我们衡量在选择近似值时损失了多少信息。
在信息论或概率论中,KL散度(Kullback–Leibler divergence),又称为相对熵(relative entropy),是一种描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q)≠D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中Q表示真实分布,Q表示P的拟合分布。
对一个离散随机变量或连续随机变量的两个概率分布P和Q来说KL散度的定义分别如下所示
$D(P||Q) = ∑ i ∈ X P ( i ) ∗ [ l o g ( P ( i ) Q ( i ) ) ] \sum_{i\in{X}}P(i) * [log(\frac {P(i)}{Q(i)})] ∑i∈XP(i)∗[log(Q(i)P(i))]
$D(P||Q) = ∫ x P ( x ) ∗ [ l o g ( P ( i ) Q ( i ) ) ] d x \int_{x}P(x) * [log(\frac {P(i)}{Q(i)})]dx ∫xP(x)∗[log(Q(i)P(i))]dx
但似乎还是有点难以理解为什么KL散度就可以衡量两个分布之间的匹配程度了,下面举例说明。
举例探索
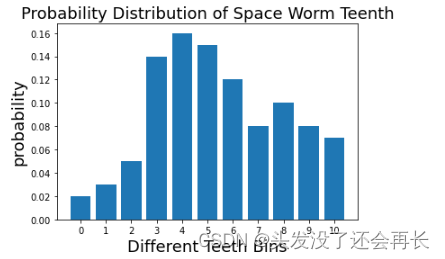
假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫,这些太空蠕虫的牙齿数量各不相同,在收集和许多样本后,我们得出了蠕虫牙齿数量的经验概率分布,用数组表示true_data=[0.02, 0.03, 0.05, 0.14, 0.16, 0.15, 0.12, 0.08, 0.1, 0.08, 0.07]。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高,所以我们需要用尽量少的数据表达这些信息。我们有个好方法:我们不发送单个数值,而是绘制一张图表。这样就将数据转化为分布。
可视化如下:
true_data=[0.02, 0.03, 0.05, 0.14, 0.16, 0.15, 0.12, 0.08, 0.1, 0.08, 0.07]
assert sum(true_data)==1.0pylab.bar(np.arange(len(true_data)), true_data)
pylab.xlabel('Different Teeth Bins', fontsize=18)
pylab.title('Probability Distribution of Space Worm Teenth', fontsize=18)
pylab.ylabel("probability", fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.show()
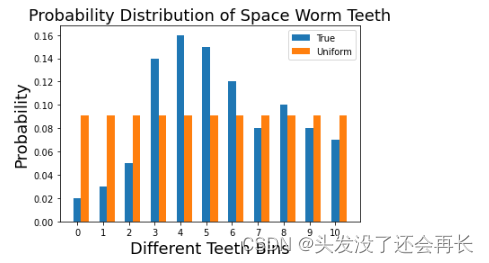
简化尝试:均匀分布(Uniform distribution)
这些数据很好,但是我们想更加简化这些数据,第一个选择是均匀分布。上面的概率数据转化为均匀分布。一共11个样本,所以每一个牙齿数量的概率都是1/11。
def get_unif_probability(n):return 1.0/nunif_data = [get_unif_probability(11) for _ in range(11)]
width=0.3pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data))+width,unif_data,width=width,label='Uniform')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()
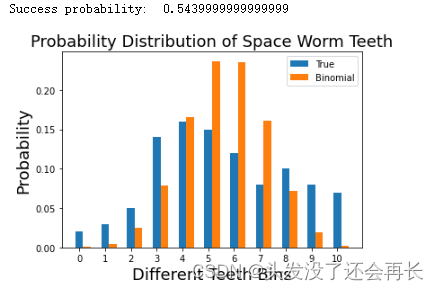
简化尝试:二项分布(binomial distribution)
显然我们的数据不是均匀分布的,现在尝试另一种二项分布对数据进行建模。我们需要计算二项分布的概率参数p,本例中n=10,E(X)=5.7,由E(X)=np得到p=0.57。则对于每一类牙齿个数的概率可以使用以下公式计算:
P ( X = i ) = C n k p k ( 1 − p ) ( n − k ) P(X=i)=C_n^kp^k(1-p)^{(n-k)} P(X=i)=Cnkpk(1−p)(n−k) i=(1,2,…)
def get_bino_probability(mean,k,n):return (factorial(n)/(factorial(k)*factorial(n-k)))*(mean**k)*((1.0-mean)**(n-k))def get_bino_success(true_data,n):return np.sum(np.array(true_data)*np.arange(len(true_data)))/10.0n_trials = 10
succ = get_bino_success(true_data,n_trials)
print('Success probability: ',succ)bino_data = [get_bino_probability(succ,k,n_trials) for k in range(11)]width=0.3pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()
汇总分析
现在我们使用了两个分布去近似我们原始的概率分布,将它们绘制在同一个图中进行比较,如下图所示:
pylab.bar(np.arange(len(true_data))-width,true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data)),unif_data,width=width,label='Uniform')
pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()
 可以看到这两个分布都没有很好的近似我们的原始数据,但是我们需要衡量一下哪个更好。
可以看到这两个分布都没有很好的近似我们的原始数据,但是我们需要衡量一下哪个更好。
我们最开始关注的就是如何使发送的信息最少,两个方法都减少了参数量,我们可以看哪个携带了更多的信息,这就是KL散度的作用。
熵
KL起源于信息论,信息论的主要目标是量化数据中有多少信息。某个信息 x i x_i xi出现的不确定的大小定义为 x i x_i xi所携带的信息量,用 I ( x i ) I(x_i) I(xi)表示, I ( x i ) I(x_i) I(xi)与信息 x i x_i xi出现的概率 p ( x i ) p(x_i) p(xi)之间的关系为:
I ( x i ) = l o g 1 p ( x i ) = − l o g p ( x i ) I(x_i) = log\frac{1}{p(x_i)} = -logp(x_i) I(xi)=logp(xi)1=−logp(xi)
信息论中最重要的指标称为熵,通常表示为H。概率分布的熵的定义时:
H = − ∑ i = 1 N p ( x i ) l o g p ( x i ) H = - \sum_{i=1}^Np(x_i)logp(x_i) H=−∑i=1Np(xi)logp(xi)
如果我们在计算中使用2为底的对数,我们可以将熵解释为“编码所需的最小比特数”。在这种情况下,信息是指根据我们的经验分布给出的每个牙齿计数观察。根据我们观察到的数据,我们的概率分布的熵为3.12比特。比特数告诉我们,在平均情况下,我们需要多少比特来编码我们在单个情况下观察到的牙齿数量的下限。
但是,熵并不能告诉我们最佳的编码方案,以帮助我们实现这种压缩。最优编码是一个非常有趣的话题,但对于理解KL散度并不是必要的。熵的关键是,仅仅知道我们需要的比特数的理论下限,我们有一种方法来准确量化数据中包含的信息量。 现在我们可以量化这一点,我们想要量化的是当我们用参数化的近似替代我们观察到的分布时丢失了多少信息。
使用KL散度测量丢失的信息
Kullback-Leibler散度只是对我们的熵公式的略微修改。不仅仅是有我们的概率分布p,还有上近似分布q。然后,我们查看每个log值的差异:
$D(p||q) = ∑ i ∈ X p ( i ) ∗ [ l o g ( p ( i ) q ( i ) ) ] \sum_{i\in{X}}p(i) * [log(\frac {p(i)}{q(i)})] ∑i∈Xp(i)∗[log(q(i)p(i))]
利用KL散度,我们可以精确地计算出当我们近似一个分布与另一个分布时损失了多少信息。让我们回到我们的数据,看看结果如何。
比较我们的近似分布
def get_klpq_div(p_probs, q_probs):kl_div = 0.0for pi, qi in zip(p_probs, q_probs):kl_div += pi*np.log(pi/qi)return kl_divdef get_klqp_div(p_probs, q_probs):kl_div = 0.0for pi, qi in zip(p_probs, q_probs):kl_div += qi*np.log(qi/pi)print('KL(True||Uniform): ',get_klpq_div(true_data,unif_data))
print('KL(True||Binomial): ',get_klpq_div(true_data,bino_data))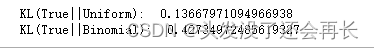
从计算的KL结果来看,使用二项分布损失的信息大于使用均匀分布损失的信息,所以我们最后如果从中选择一个,还是会选择均匀分布。
参考文章:
Kullback-Leibler(KL)散度介绍
KL散度代码地址
相关文章:
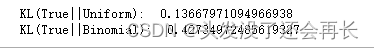
机器学习-KL散度的直观理解+代码
KL散度 直观理解:KL散度是一种衡量两个分布之间匹配程度的方法。通常在概率和统计中,我们会用更简单的近似分布来代替观察到的数据或复杂的分布,KL散度帮我们衡量在选择近似值时损失了多少信息。 在信息论或概率论中,KL散度&#…...
【教程】制作 iOS 推送证书
目录 证书类型 MAC Key Store 消息推送控制台 制作证书 创建苹果 App ID 使用appuploder制作 .p12文件 创建证书 如需向 iOS 设备推送数据,您首先需要在消息推送控制台上配置 iOS 推送证书。iOS 推送证书用于推送通知,本文将介绍消息推送服务支…...
ToolLLM model 以及LangChain AutoGPT Xagent在调用外部工具Tools的表现对比浅析
文章主要谈及主流ToolLLM 以及高口碑Agent 在调用Tools上的一些对比,框架先上,内容会不断丰富与更新。 第一部分,ToolLLM model 先来说主打Function Call 的大模型们 OpenAI GPT 宇宙第一LLM,它的functionCall都知道࿰…...
【MySQL学习之基础篇】约束
文章目录 1. 概述2. 基础约束3. 外键约束3.1. 介绍3.2. 外键的添加3.3. 外键删除和更新行为 1. 概述 概念: 约束是作用于表中字段上的规则,用于限制存储在表中的数据。 目的: 保证数据库中数据的正确、有效性和完整性。 分类&#x…...
【DataSophon】大数据管理平台DataSophon-1.2.1基本使用
🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 🪁🍁🪁&am…...
基于redisson实现发布订阅(多服务间用避坑)
前言 今天要分享的是基于Redisson实现信息发布与订阅(以前分享过直接基于redis的实现),如果你是在多服务间基于redisson做信息传递,并且有服务压根就收不到信息,那你一定要看完。 今天其实重点是避坑࿰…...

Java 源码、反码、补码 位运算
文章目录 1. 源码、反码、补码1.1 原码1.2 反码1.3 补码1.4 byte的最大值1.5 byte的最小值 2. 位运算2.1 & 与2.2 | 或2.3 ~ 非2.4 ^ 异或2.5 << 左移 (没有无符号左移)2.6 >> 右移 (有符号右移)2.7 >>>…...
时序分解 | Matlab实现NGO-ICEEMDAN基于北方苍鹰算法优化ICEEMDAN时间序列信号分解
时序分解 | Matlab实现NGO-ICEEMDAN基于北方苍鹰算法优化ICEEMDAN时间序列信号分解 目录 时序分解 | Matlab实现NGO-ICEEMDAN基于北方苍鹰算法优化ICEEMDAN时间序列信号分解效果一览基本介绍程序设计参考资料 效果一览 基本介绍 Matlab实现NGO-ICEEMDAN基于北方苍鹰算法优化ICE…...
Linux Conda 安装 Jupyter
在Linux服务器Conda环境上安装Jupyter过程中遇到了无数的报错,特此记录。 目录 步骤一:安装Anaconda3 步骤二:配置Conda源 步骤三:安装Jupyter 安装报错:simplejson.errors.JSONDecodeError 安装报错:…...

金融众筹系统源码:适合创业孵化机构 附带完整的搭建教程
互联网技术的发展,金融众筹作为一种新型的融资方式,逐渐成为创业孵化机构的重要手段。为了满足这一需求,金融众筹系统源码就由此而生,并附带了完整的搭建教程。 以下是部分代码示例: 系统特色功能一览: 1.…...

OpenCV imencode 函数详解与应用示例
OpenCV imencode 函数详解与应用示例 介绍imencode 函数的基本信息示例代码应用场景 介绍 OpenCV是一个强大的计算机视觉库,提供了许多图像处理和分析的工具。imencode函数是其中之一,用于将图像编码为指定格式的字节流。这个函数对于图像的存储、传输和…...
持续集成交付CICD:Jenkins使用CD流水线下载Nexus制品
目录 一、实验 1.Jenkins使用CD流水线下载Nexus制品 一、实验 1.Jenkins使用CD流水线下载Nexus制品 (1)Jenkins新建CD流水线 (2)新建视图 (3)查看视图 (4)添加字符参数 …...
)
【C++】输入输出流 ⑩ ( 文件流 | 文件流打开方式参数 | 文件指针 | 组合打开方式 | 文件打开失败 )
文章目录 一、文件流打开方式参数1、文件流打开方式参数2、文件指针3、组合打开方式4、文件打开失败 一、文件流打开方式参数 1、文件流打开方式参数 文件流打开方式参数 : ios::in : 以只读方式打开文件 ;ios::out : 以只写方式打开文件 , 默认打开方式 , 如果文件已存在则清…...

React中的setState执行机制
我这里今天下雨了,温度一下从昨天的22度降到今天的6度,家里和学校已经下了几天雪了,还是想去玩一下的,哈哈,只能在图片里看到了。 一. setState是什么 它是React组件中用于更新状态的方法。它是类组件中的方法&#x…...

LabVIEW实时建模检测癌细胞的异常
LabVIEW实时建模检测癌细胞的异常 癌症是全球健康的主要挑战之一,每年导致许多人死亡。世界卫生组织指出,不健康的生活方式和日益严重的环境污染是癌症发生的主要原因之一。癌症的发生通常与基因突变有关,这些突变导致细胞失去正常的增长和分…...

Python卡尔曼滤波器OpenCV跟踪和预测物体的轨迹
模拟简单物体二维运动和预测位置 预测数学式 想象一下你正坐在一辆汽车里,在雾中行驶。 你几乎看不到路,但你有一个 GPS 系统可以告诉你你的速度和位置。 问题是,这个 GPS 并不完美; 它有时会产生噪音或不准确的读数。 您如何知…...

LeetCode Hot100 25.K个一组翻转链表
题目: 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯…...

中职网络安全应急响应—Server2228
应急响应 任务环境说明: 服务器场景:Server2228(开放链接) 用户名:root,密码:p@ssw0rd123 1. 找出被黑客修改的系统别名,并将倒数第二个别名作为Flag值提交; 通过用户名和密码登录系统 在 Linux 中,利用 “alias” 命令去查看当前系统中定义的所有别名 flag:ss …...

springboot 获取路径
PostConstructpublic void setup() {try {// jar包所在目录 /Users/mashanshanString path this.getClass().getProtectionDomain().getCodeSource().getLocation().getPath();System.out.println("path:" path); // file:/Users/mashanshan/manual-admin-0.0.1-…...

C#上位机与欧姆龙PLC的通信01----项目背景
最近,【西门庆】作为项目经理负责一个70万的北京项目,需要在工控系统集成软件开发中和欧 姆龙PLC对接,考虑项目现场情况优先想到了采用FinsTCP通讯协议,接下来就是记录如何一步步实现这些通讯过程的,希望给电气工程师&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
