一文读懂算法中的时间复杂度和空间复杂度,O(1)、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度
时间复杂度和空间复杂度是什么
时间复杂度(Time Complexity)是描述算法运行时间长短的一个度量。空间复杂度(Space Complexity)是描述算法在运行过程中所需要的存储空间大小的一个度量。
时间复杂度和空间复杂度是衡量算法性能的重要指标。在实际开发中,我们通常会选择时间复杂度和空间复杂度都较低的算法。
时间复杂度可以用大O表示法来表示。大O表示法是用一个大写字母O来表示一个函数的增长率。例如,一个函数f(n)的增长率为O(n),表示当n趋于无穷大时,f(n)的增长率与n的增长率相同。
空间复杂度也可以用大O表示法来表示。例如,一个函数f(n)的空间复杂度为O(n),表示当n趋于无穷大时,f(n)所需要的存储空间与n的增长率相同。
在实际开发中,我们通常会选择时间复杂度和空间复杂度都较低的算法。例如,在排序算法中,我们通常会选择快速排序算法,而不是冒泡排序算法。这是因为快速排序算法的时间复杂度为O(nlogn),而冒泡排序算法的时间复杂度为O(n^2)。
常见的时间复杂度有哪些?
O(1):常数时间复杂度。表示算法运行时间与输入数据的大小无关。例如,求一个数的绝对值,无论这个数是多少,算法运行时间都是常数。
| 例如:访问数组元素:如果我们有一个长度为n的数组,并且我们想要访问数组中的某个元素,那么无论n多大,访问该元素的时间复杂度都是O(1)。因为访问数组元素只需要一个固定的时间,与数组的大小无关。 |
算法实现:
/*** 我们只处理数组中的第一个元素,无论数组中有多少个元素,* 算法的运行时间是固定的,所以时间复杂度为O(1)。** @param arr 数组*/public int constantTimeAlgorithm(int[] arr) {int firstElement = arr[0];// 在这里进行处理第一个元素的操作// ...return firstElement;}O(logn):对数时间复杂度。表示算法运行时间与输入数据的对数成正比。例如,二分查找算法。
| 你可以这样理解: 假设你有一个长度为n的数列,你想找到某个数在数列中的位置。如果用顺序查找,你需要遍历整个数列,时间复杂度为O(n)。如果用二分查找,你只需要遍历数列的一半,时间复杂度为O(logn)。 随着n的增大,O(n)的增长速度要比O(logn)快得多。例如,当n=100时,O(n)的值为100,而O(logn)的值为7。当n=1000时,O(n)的值为1000,而O(logn)的值为10。 因此,O(logn)的时间复杂度比O(n)的时间复杂度要好得多。 复习一下计算过程: 当计算 log₂(100) 时,我们要找到一个数 x,使得 2 的 x 次方等于 100。换句话说,我们要求解以下方程: 2^x = 100 为了求解这个方程,我们可以使用对数的定义。根据定义,log₂(100) 就是满足 2 的 x 次方等于 100 的 x 值。 因此,我们可以将方程改写为: x = log₂(100) 现在,我们需要计算 log₂(100) 的值。可以使用换底公式将其转化为常用对数或自然对数。换底公式如下: log₂(100) = logₓ(100) / logₓ(2) 其中,x 可以是任意正数,我们可以选择常用对数(以 10 为底)或自然对数(以 e 为底)。这里我们选择常用对数。 所以,我们有: log₂(100) = log₁₀(100) / log₁₀(2) 接下来,我们计算 log₁₀(100) 和 log₁₀(2) 的值: log₁₀(100) ≈ 2 log₁₀(2) ≈ 0.30103 将这些值代入公式中,我们可以计算出 log₂(100) 的近似值: log₂(100) ≈ log₁₀(100) / log₁₀(2) ≈ 2 / 0.30103 ≈ 6.6438561898 所以,log₂(100) 的近似值为 6.6438561898。 |
算法实现:
/*** 代码中的binarySearch方法实现了对有序数组进行二分查找的算法。* 它将目标元素与数组的中间元素进行比较,若相等则返回中间元素的索引,若小于中间元素则在左子数组中继续查找,* 若大于中间元素则在右子数组中继续查找。通过不断缩小查找范围,直到找到目标元素或发现不存在目标元素。* * @param arr 数组* @param target 目标值* @return int*/public int binarySearch(int[] arr, int target) {int low = 0;int high = arr.length - 1;while (low <= high) {int mid = low + (high - low) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {low = mid + 1;} else {high = mid - 1;}}return -1; // 如果找不到目标元素,则返回-1}O(n):线性时间复杂度。表示算法运行时间与输入数据的大小成正比。例如,冒泡排序算法。
| 你可以这样理解: 假设你有一个长度为n的数列,你想对这个数列进行排序。如果用冒泡排序,你需要遍历整个数列,然后将每个元素与它后面的元素进行比较,如果前一个元素比后一个元素大,就交换它们的位置。你需要重复这个过程,直到整个数列都被排序。 随着n的增大,O(n)的增长速度要比O(1)快得多。例如,当n=100时,O(n)的值为100,而O(1)的值为1。当n=1000时,O(n)的值为1000,而O(1)的值为1。 因此,O(n)的时间复杂度比O(1)的时间复杂度要差得多。 |
算法实现:
/*** 这个方法计算整数数组的平均值* * 在这个算法中,我们遍历整个数组一次,所以时间复杂度是O(n),其中n是数组的长度。* 这是计算数组平均值的最佳时间复杂度,因为我们至少需要查看数组中的每个元素一次。** @param array 数组*/public static double calculateAverage(int[] array) {int sum = 0;for (int i = 0; i < array.length; i++) {sum += array[i];}return (double) sum / array.length;}O(n^2):平方时间复杂度。表示算法运行时间与输入数据的平方成正比。例如,选择排序算法。
| O(n^2) 是一个表示算法复杂度的概念。简单来说,当你运行一个O(n^2)的算法时,它的运行时间或步骤的数量会随着输入大小n的增加而增加。具体来说,这个算法的复杂度是指它的运行时间或步骤的数量与n的平方成正比。 举个例子,如果你有一个数组,你想计算每个元素与所有其他元素的组合,那么你需要对每个元素进行n次比较(n是数组的大小),总共需要进行n * n = n^2次比较。因此,这个算法的时间复杂度是O(n^2)。 总结一下,O(n^2) 表示当输入大小n增加时,算法的运行时间或步骤数量会以n的平方的速度增加。 |
代码实现:
/*** 一个时间复杂度为O(n^2)的算法,常见的方法是使用嵌套循环。* 下面代码实现了一个冒泡排序算法。它通过嵌套循环遍历数组,并比较相邻的元素。* 如果前一个元素大于后一个元素,则交换它们的位置。通过多次遍历和交换,* 较大的元素会逐渐向数组的末尾冒泡。* 这个过程将重复执行n-1次,每次循环都需要比较n-i-1次。因此,总的比较次数为:** n-1 + n-2 + ... + 1 = n * (n-1) / 2,** 最终得到时间复杂度为O(n^2)。** @param arr 数组*/public void bubbleSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换arr[j]和arr[j + 1]int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}O(n^3):立方时间复杂度。表示算法运行时间与输入数据的立方成正比。
| 如果你有一个非常大的数组,并且你想计算每个元素与所有其他元素的组合的乘积,那么你需要对每个元素进行n次比较,然后再进行一次乘法操作。所以总共需要进行n * n = n^2次比较,以及n * n * n = n^3次乘法操作。因此,这个算法的时间复杂度是O(n^3)。 |
O(2^n):指数时间复杂度。表示算法运行时间与输入数据的指数成正比。例如,汉诺塔问题,斐波那契数列。
| 斐波那契数列:斐波那契数列是一个非常著名的数列,其中每个数字都是前两个数字的和。对于斐波那契数列的第n项,我们可以通过递归或迭代来计算。但是,由于递归的重复计算,其时间复杂度是O(2^n)。这是因为每次递归都会生成一个新的项,导致重复计算大量前面的项,因此总体时间复杂度是指数级的增长。 |
算法实现:
/*** 这个代码中,generatePowerSet方法会生成一个数组的所有子集。* 我们通过两个嵌套的循环来实现这一点。外部循环遍历2^n个可能的子集* (因为每个元素都可以在子集中或不在子集中,所以总共有2^n个子集),* 内部循环则根据当前子集的二进制表示来决定是否将数组中的元素添加到子集中。* 如果二进制表示的某一位为1,那么就将对应的元素添加到子集中。* * @param array 数组* @return List<List<Integer>>*/public static List<List<Integer>> generatePowerSet(int[] array) {List<List<Integer>> powerSet = new ArrayList<>();int n = array.length;for (int i = 0; i < (1 << n); i++) {List<Integer> subset = new ArrayList<>();for (int j = 0; j < n; j++) {if (((i >> j) & 1) == 1) {subset.add(array[j]);}}powerSet.add(subset);}return powerSet;}常见的空间复杂度有哪些?
算法的空间复杂度是评估算法在执行过程中所需额外存储空间的重要指标。以下是算法空间复杂度的一些常见类型:
- 常数空间复杂度(O(1)):算法执行过程中仅需要固定大小的额外空间。无论输入规模大小,所需的额外空间保持不变。
- 线性空间复杂度(O(n)):算法执行过程中所需的额外空间与输入规模线性相关。随着输入规模的增长,所需的空间也按比例增长。
- 对数空间复杂度(O(log n)):算法执行过程中所需的额外空间与输入规模的对数成正比。即使输入规模较大,所需的额外空间也会相对较少。
- 平方空间复杂度(O(n^2)):算法执行过程中所需的额外空间与输入规模的平方成正比。随着输入规模的增长,所需的空间会以平方的速度增长。
- 立方空间复杂度(O(n^3)):算法执行过程中所需的额外空间与输入规模的立方成正比。随着输入规模的增长,所需的空间会以立方的速度增长。
- 指数空间复杂度(O(2^n)):算法执行过程中所需的额外空间与输入规模的指数成正比。随着输入规模的增长,所需的空间会以指数的速度增长。
这些空间复杂度类型可以用于评估算法在处理不同规模输入时所需的额外存储空间的大小。选择合适的算法和数据结构可以优化空间复杂度,以适应不同规模的需求。
相关文章:
、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度)
一文读懂算法中的时间复杂度和空间复杂度,O(1)、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度
时间复杂度和空间复杂度是什么 时间复杂度(Time Complexity)是描述算法运行时间长短的一个度量。空间复杂度(Space Complexity)是描述算法在运行过程中所需要的存储空间大小的一个度量。 时间复杂度和空间复杂度是衡量算法性能…...
LWIP热插拔功能实现
0 工具准备 1.lwip 1.4.1 2.RTOS(本文使用rt-thread)1 使能连接变化回调功能 打开lwipopts.h,将宏定义LWIP_NETIF_LINK_CALLBACK的值设为1,如下: #define LWIP_NETIF_LINK_CALLBACK 1这个宏定义被使能后会将…...
android下的app性能测试应主要针对那些方面,如何开展?
如何开展安卓手机下的App性能测试,对于优秀的测试人员而言,除了要懂得性能测试的步骤流程外,还应该懂的性能测试的一些其他知识,比如性能测试指标、各指标的意义,常用的性能测试工具、如何查看结果分析等等知识。所以本…...
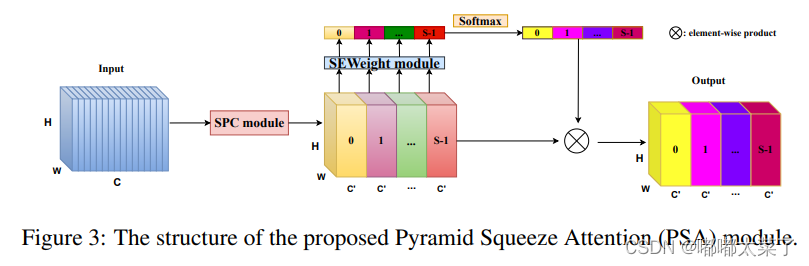
【深度学习】注意力机制(二)
本文介绍一些注意力机制的实现,包括EA/MHSA/SK/DA/EPSA。 【深度学习】注意力机制(一) 【深度学习】注意力机制(三) 目录 一、EA(External Attention) 二、Multi Head Self Attention 三、…...
学习黑马vue
项目分析 项目下载地址:vue-admin-template-master: 学习黑马vue 项目下载后没有环境可参考我的篇文章,算是比较详细:vue安装与配置-CSDN博客 安装这两个插件可格式化代码,vscode这个软件是免费的,官网:…...
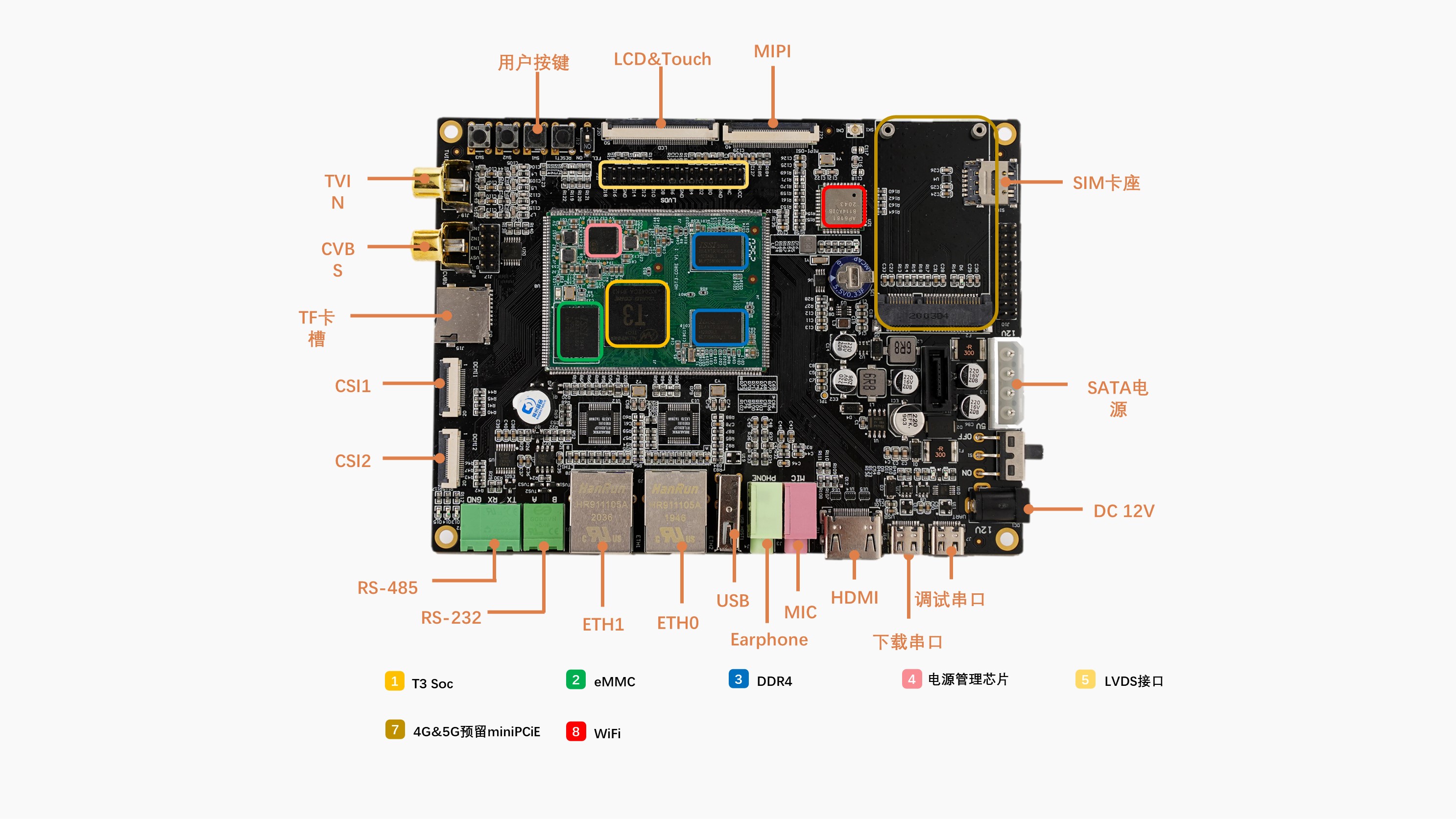
gdb本地调试版本移植至ARM-Linux系统
移植ncurses库 本文使用的ncurses版本为ncurses-5.9.tar.gz 下载地址:https://ftp.gnu.org/gnu/ncurses/ncurses-5.9.tar.gz 1. 将ncurses压缩包拷贝至Linux主机或使用wget命令下载并解压 tar-zxvf ncurses-5.9.tar.gz 2. 解压后进入到ncurses-5.9目录…...
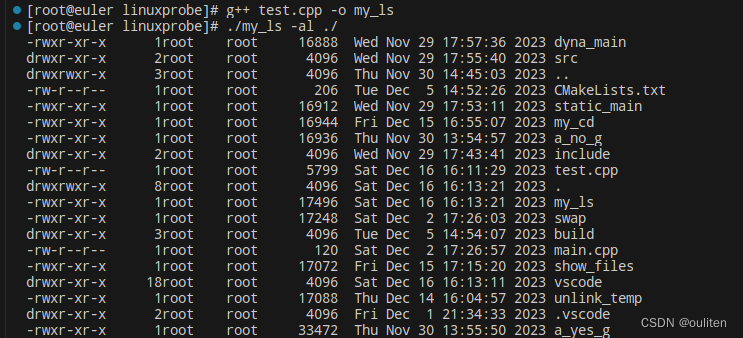
《Linux C编程实战》笔记:实现自己的ls命令
关键函数的功能及说明 1.void display_attribute(struct stat buf,char *name) 函数功能:打印文件名为name的文件信息,如 含义分别为:文件的类型和访问权限,文件的链接数,文件的所有者,文件所有者所属的组…...
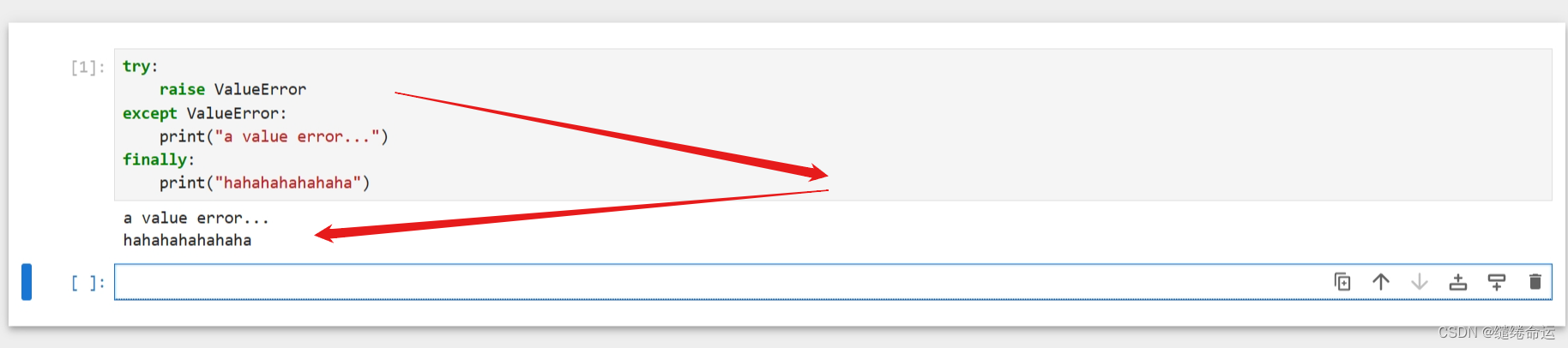
Python个人代码随笔(观看无益,请跳过)
异常抛错:一般来说,在程序中,遇到异常时,会从这一层逐层往外抛错,一直抛到最外层,由最外层把错误显示在用户终端。 try:raise ValueError("A value error...") except ValueError:print("V…...

Unity中实现ShaderToy卡通火(总结篇)
文章目录 前言一、把卡通火修改为后处理效果1、在Shader属性面板定义属性接收帧缓存纹理2、在片元着色器对其纹理采样后,与卡通火相加输出请添加图片描述 二、我们自定义卡通火1、修改 _CUTOFF 使卡通火显示在屏幕两侧2、使火附近屏幕偏红色 前言 在之前的文章中&a…...

等保2.0的变化
1法律地位得到确认 《中华人民共和国网络安全法》第21条规定“国家实行网络安全等级保护制度”,要求“网络运营者应当按照网络安全等级保护制度要求,履行安全保护义务”;第31条规定“对于国家关键信息基础设施,在网络安全等级保护…...
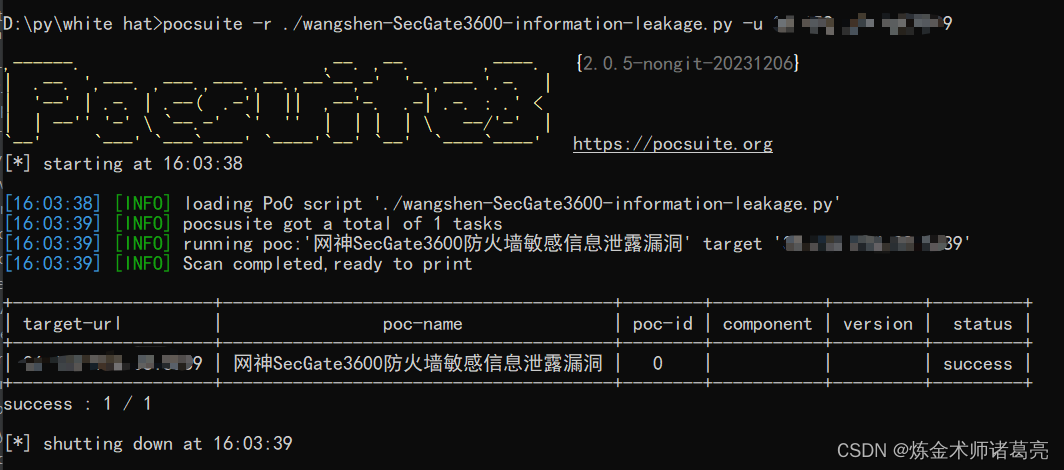
漏洞复现-网神SecGate3600防火墙敏感信息泄露漏洞(附漏洞检测脚本)
免责声明 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…...

ArkTS入门
代码结构分析 struct Index{ } 「自定义组件:可复用的UI单元」 xxx 「装饰器:用来装饰类结构、方法、变量」 Entry 标记当前组件是入口组件(该组件可被独立访问,通俗来讲:它自己就是一个页面)Component 用…...

JS中for循环之退出循环
我为大家介绍一下退出循环的两种方法 1.continue 退出本次循环,一般用于排除或者跳过某一个选项的时候,可以使用continue for(let i 0;i<5;i){if(i 3){continue}// 跳过了3console.log(i) //0 1 2 4}2.break 退出整个for循环,一般用于…...
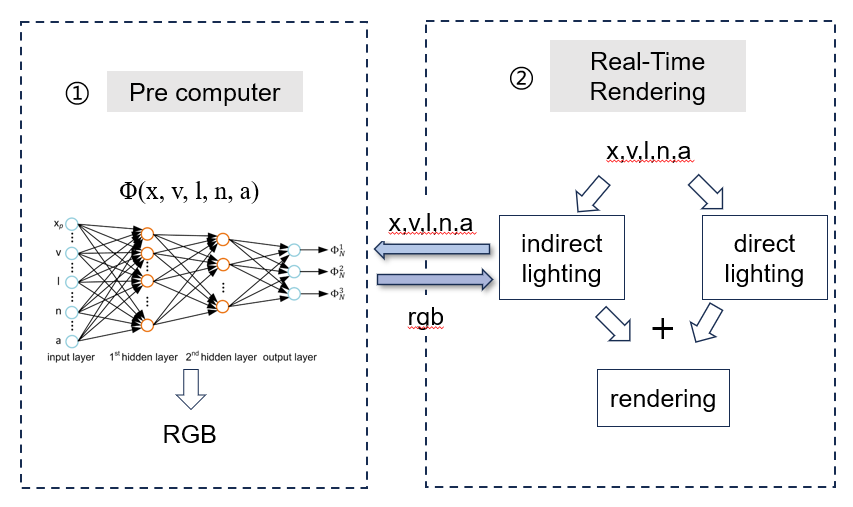
《Global illumination with radiance regression functions》
总结一下最近看的这篇结合神经网络的全局光照论文。 论文的主要思想是利用了神经网络的非线性特性去拟合全局光照中的间接光照部分,采用了基础的2层MLP去训练,最终能实现一些点光源、glossy材质的光照渲染。为了更好的理解、其输入输出表示如下。 首先…...

华南理工C++试卷
诚信应考 , 考试作弊将带来严重后果! 《C程序设计试卷》 注意事项:1. 考前请将密封线内填写清楚; 2. 所有答案请答在试卷的答案栏上; 3.考试形式:闭卷 4. 本试卷共 五 大题,满分100分ÿ…...
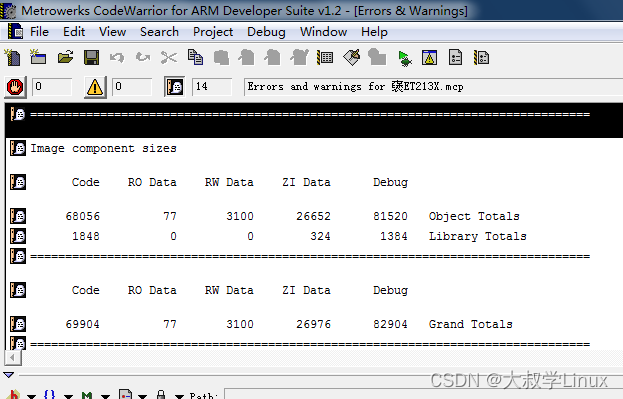
0001.WIN7(64位)安装ADS1.2出现L6218错误
用了十多年的笔记本电脑系统出现问题,硬件升级重装以后安装ADS1.2。在编译代码的时候出现L6218错误。如下: 图片是从网上找的,我编译出错的界面没有保留下来。 首先,代码本身没有任何问题 ,代码在win7(32位)下编译没有…...
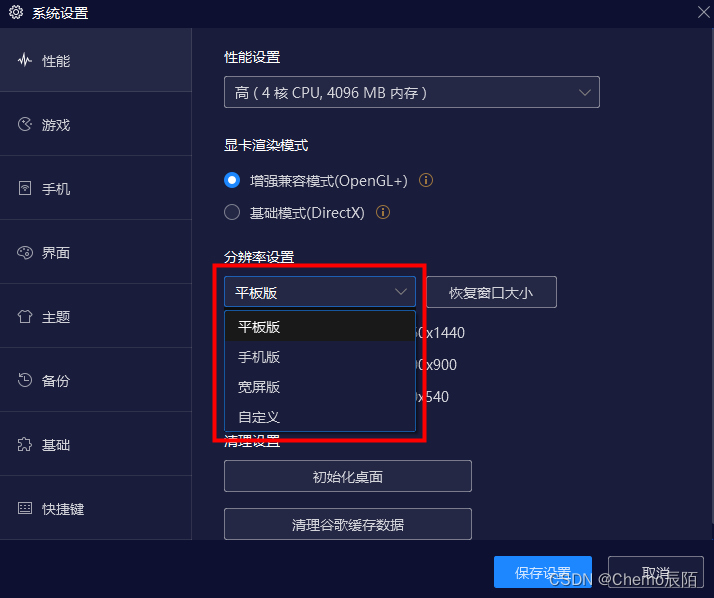
HBuilderX 配置 夜神模拟器 详细图文教程
在电脑端查看App的效果,不用真机调试,下载一个模拟器就可以了 --- Nox Player,夜神模拟器,是一款 Android 模拟器。他的使用非常安全,最重要的是完全免费。 一. 安装模拟器 官网地址: (yeshen.com) 二.配…...
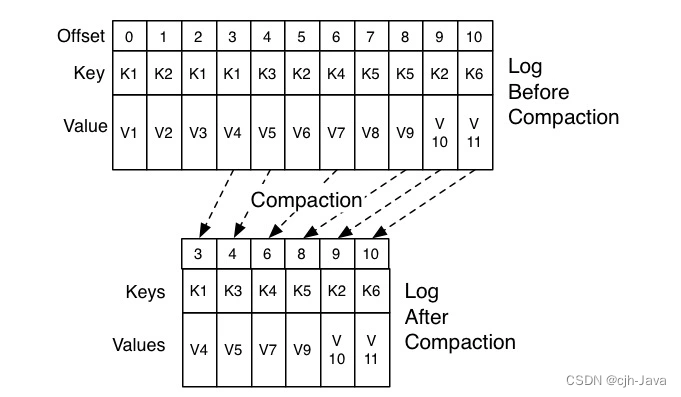
10、神秘的“位移主题”
神秘的“位移主题” 1、什么是位移主题2、位移主题的消息格式3、位移主题是怎么被创建的4、什么地方会用到位移主题5、位移主题的删除机制 本章主题是:Kafka 中的内部主题(Internal Topic)__consumer_offsets。 __consumer_offsets 在 Kafka …...

【Linux】dump命令使用
dump命令 dump命令用于备份文件系统。使用dump命令可以检查ext2/3/4文件系统上的文件,并确定哪些文件需要备份。这些文件复制到指定的磁盘、磁带或其他存储介质保管。 语法 dump [选项] [目录|文件系统] bash: dump: 未找到命令... 安装dump yum -y install …...

使用 TensorFlow 创建生产级机器学习模型(基于数据流编程的符号数学系统)——学习笔记
资源出处:初学者的 TensorFlow 2.0 教程 | TensorFlow Core (google.cn) 前言 对于新框架的学习,阅读官方文档是一种非常有效的方法。官方文档通常提供了关于框架的详细信息、使用方法和示例代码,可以帮助你快速了解和掌握框架的使用。 如…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
