2023第十四届蓝桥杯国赛 C/C++ 大学 B 组
文章目录
- 前言
- 试题 A: 子 2023
- 作者思考
- 题解
- 答案
- 试题 B: 双子数
- 作者思考
- 题解
- 试题 C: 班级活动
- 作者思考
- 题解
- 试题 D: 合并数列
- 作者思考
- 题解
- 试题 E: 数三角
- 作者思考
- 题解
- 试题 F: 删边问题
- 作者思考
- 题解
- 试题 G: AB 路线
- 作者思考
- 题解
- 试题 H: 抓娃娃
- 作者思考
- 题解
- 试题 I: 拼数字
- 试题 J: 逃跑
前言
第一次接触写国赛的题,在下才疏学浅,题解如有错误请指正。🤗
A ~ H有题解,其中E题作者打的暴力。
如果能帮助你的话,点点赞吧!谢谢🤝
试题 A: 子 2023
本题总分:5 分
【问题描述】
小蓝在黑板上连续写下从 1 到 2023 之间所有的整数,得到了一个数字序列:
S = 12345678910111213 . . . 20222023。
小蓝想知道 S 中有多少种子序列恰好等于 2023?
提示,以下是 3 种满足条件的子序列(用中括号标识出的数字是子序列包含的数字):
1[2]34567891[0]111[2]1[3]14151617181920212223…
1[2]34567891[0]111[2]131415161718192021222[3]…
1[2]34567891[0]111213141516171819[2]021222[3]…
注意以下是不满足条件的子序列,虽然包含了 2、0、2、3 四个数字,但是顺序不对:
1[2]345678910111[2]131415161718192[0]21222[3]…
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分
作者思考
作完省赛的就知道,这不就是省赛E题的接龙数列嘛😅。简单的dp就可以。分别以2 0 2 3(要转化,因为有两个2)结尾dp就可以了👻。
虽然正解是dp,但是暴力 + 剪枝也可以做,就是跑的有些慢。作者本地跑差不多50s。
还一个坑,就是如果你不开long long就会得到错的答案:1189693313
题解
#include<bits/stdc++.h>
using namespace std;
#define int long long // 开long long string s; int f1() {int cnt = 0;for (int a = 0; a < s.size(); a++) {if (s[a] != '2') continue;for (int b = a + 1; b < s.size(); b++) {if (s[b] != '0') continue;for (int c = b + 1; c < s.size(); c++) {if (s[c] != '2') continue;for (int d = c + 1; d < s.size(); d++) {if (s[d] != '3') continue;cnt++;}}}}return cnt;
}int f2() {int dp[4] = {0}; // 分别代表"2"、"20"、"202"、"2023"的数量for (char ch : s) {if (ch == '2') {dp[0]++;dp[2] += dp[1];}if (ch == '0') dp[1] += dp[0];if (ch == '3') dp[3] += dp[2];}return dp[3];
}signed main(){for (int i = 1; i <= 2023; i++) { // 剪枝 string tmp = to_string(i);for (char ch : tmp) {if (ch == '2') s += '2';if (ch == '0') s += '0';if (ch == '3') s += '3';}}
// cout << f1() << endl; // 暴力 cout << f2() << endl; // dpreturn 0;
}答案
5484660609
试题 B: 双子数
本题总分:5 分
【问题描述】
若一个正整数 x 可以被表示为 p 2 ^2 2 × q 2 ^2 2,其中 p、q 为质数且 p , q,则 x 是一个 “双子数”。请计算区间 [2333, 23333333333333] 内有多少个 “双子数”?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
作者思考
首先第一眼看到质数,那么直接就是质数筛嘛。筛多少质数呢?看区间数量级是10 14 ^{14} 14 ,难道筛10 14 ^{14} 14 ?🤔
不用, p、q 的最大值 23333333333333 \sqrt{23333333333333} 23333333333333 ≈ \approx ≈ 4830459。 所以大约筛5 x 10 6 ^6 6就可以了。
还有一个坑 ,计算p 2 ^2 2 × q 2 ^2 2 时,遍历到最大的p、q ,大约是10 24 ^{24} 24 ,那么数量级会爆long long。解决办法1、用int128 2、缩小数据范围,开根号转化成 p x q 在范围 [ 2333 \sqrt{2333} 2333, 23333333333333 \sqrt{23333333333333} 23333333333333] ,这样就完美解决了!😼
题解
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxl = 1e7 + 7;int l = 2333, r = 23333333333333;
int ans;
vector<int> prime;
int flag[maxl];void euler_prime(int n) {for (int i = 2; i <= n; i++) {if (!flag[i]) prime.push_back(i);for (int p : prime) {flag[p * i] = 1;if (i % p == 0 || p * i > n) break;}}
}signed main () {euler_prime(5e6 + 7);for (int i = 0; i < prime.size(); i++) {for (int j = i + 1; j < prime.size(); j++) {int x = prime[i] * prime[j]; // 这里的x是题目中的x开根号if (x < pow(l, 0.5)) continue; if (x > pow(r, 0.5)) break; // 太大后面的数都不用看了,都大于范围ans++; }}cout << ans << endl;return 0;
}
试题 C: 班级活动
时间限制: 1.0s 内存限制: 256.0MB 本题总分:10 分
【问题描述】
小明的老师准备组织一次班级活动。班上一共有 n 名(n 为偶数)同学,老师想把所有的同学进行分组,每两名同学一组。为了公平,老师给每名同学随机分配了一个 n 以内的正整数作为 id,第 i 名同学的 id 为 a i _i i。
老师希望通过更改若干名同学的 id 使得对于任意一名同学 i,有且仅有另一名同学 j 的 id 与其相同(a i _i i = a j _j j)。请问老师最少需要更改多少名同学的 id?
【输入格式】
输入共 2 行。
第一行为一个正整数 n。
第二行为 n 个由空格隔开的整数 a 1 _1 1, a 2 _2 2, …, a i _i i。
【输出格式】
输出共 1 行,一个整数。
【样例输入】
4
1 2 2 3
【样例输出】
1
【样例说明】
仅需要把 a 1 _1 1 改为 a 3 _3 3 或者把 a 3 _3 3改为 a 1 _1 1 即可。
【评测用例规模与约定】
对于 20% 的数据,保证 n ≤ 10 3 ^3 3。
对于 100% 的数据,保证 n ≤ 10 5 ^5 5。
作者思考
这里看两组样例就能明白规律了
输入:
1 2 2 2 2 2 3
输出:
3
这里很显然就是3个2要变成1, 3,和一个其他数字。
输入:
1 2 2 2 3 4
输出:
2
这里很显然就是1个2要变成1(或者3, 4),剩下两个数字再合并。
结论: 配对超过2个同学的数字总和,设为cnt1, 没有完成配对的同学的数字总和,设为cnt2,
当cnt1 > cnt2时,输出cnt1
当cnt1 < cnt2时,输出cnt1 + (cnt2 - cnt1) / 2
时间复杂度:O(n)
题解
#include <bits/stdc++.h>
using namespace std;
const int maxl = 1e5 + 7;int n, cnt1, cnt2;
int a[maxl];
map<int,int> mp;
bool flag[maxl];int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];mp[a[i]]++;}for (int i = 1; i <= n; i++) {if (!flag[a[i]]) {if (mp[a[i]] == 1) cnt2++;else if (mp[a[i]] > 2) cnt1 += (mp[a[i]] - 2);flag[a[i]] = 1;} }if (cnt1 > cnt2) cout << cnt1 << endl;else cout << cnt1 + (cnt2 - cnt1) / 2 << endl;return 0;
}
试题 D: 合并数列
时间限制: 1.0s 内存限制: 256.0MB 本题总分:10 分
【问题描述】
小明发现有很多方案可以把一个很大的正整数拆成若干正整数的和。他采取了其中两种方案,分别将他们列为两个数组 {a 1 _1 1, a 2 _2 2, …, a n _n n} 和 {b 1 _1 1, b 2 _2 2, …, b m _m m}。两个数组的和相同。
定义一次合并操作可以将某数组内相邻的两个数合并为一个新数,新数的值是原来两个数的和。小明想通过若干次合并操作将两个数组变成一模一样,即 n = m 且对于任意下标 i 满足 a i _i i = b i _i i。请计算至少需要多少次合并操作可以完成小明的目标。
【输入格式】
输入共 3 行。
第一行为两个正整数 n, m。
第二行为 n 个由空格隔开的整数 a 1 _1 1, a 2 _2 2, …, a n _n n。
第三行为 m 个由空格隔开的整数 b 1 _1 1, b 2 _2 2, …, b m _m m。
【输出格式】
输出共 1 行,一个整数。
【样例输入】
4 3
1 2 3 4
1 5 4
【样例输出】
1
【样例说明】
只需要将 a 2 _2 2 和 a 3 _3 3 合并,数组 a 变为 {1, 5, 4},即和 b 相同。
【评测用例规模与约定】
对于 20% 的数据,保证 n, m ≤ 10 3 ^3 3。
对于 100% 的数据,保证 n, m ≤ 10 5 ^5 5,0 < a i _i i , b i _i i ≤ 10 5 ^5 5。
作者思考
作者个人觉得不会这道题的人,大概率是没看到题目中的,相邻的两个数 。这里我给的大家标出来了。
看到这就应该是迎刃而解了,贪心就可以了。直接放代码了,我觉得你一定看的懂的!🤗
时间复杂度:O(n)
题解
#include<bits/stdc++.h>
using namespace std;int n, m, ans;
int tp1, tp2;
queue<int> q1, q2;int main(){cin >> n >> m;for (int i = 1, x; i <= n; i++) cin >> x, q1.push(x);for (int i = 1, x; i <= m; i++) cin >> x, q2.push(x);while (!q1.empty()) {tp1 = q1.front();tp2 = q2.front();if (tp1 == tp2) q1.pop(), q2.pop();else if (tp1 < tp2) q1.pop(), q1.front() += tp1, ans++;else q2.pop(), q2.front() += tp2, ans++;}cout << ans << endl;return 0;
}
试题 E: 数三角
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
【问题描述】
小明在二维坐标系中放置了 n 个点,他想在其中选出一个包含三个点的子集,这三个点能组成三角形。然而这样的方案太多了,他决定只选择那些可以组成等腰三角形的方案。请帮他计算出一共有多少种选法可以组成等腰三角形?
【输入格式】
输入共 n + 1 行。
第一行为一个正整数 n。
后面 n 行,每行两个整数 x i _i i, y i _i i 表示第 i 个点的坐标。
【输出格式】
输出共 1 行,一个整数。
【样例输入】
5
1 4
1 0
2 1
1 2
0 1
【样例输出】
5
【样例说明】
一共有 4 种选法:{2, 3, 4}、{3, 4, 5}、{4, 5, 2}、{5, 2, 3}、{1, 3, 5}。
【评测用例规模与约定】
对于 20% 的数据,保证 n ≤ 200。
对于 100% 的数据,保证 n ≤ 2000,0 ≤ x i _i i, y i _i i ≤ 10 9 ^9 9。
作者思考
作者思考不了了,作者不会😵💫
直接打暴力了。
时间复杂度:O(n 3 ^3 3)
题解
#include<bits/stdc++.h>
using namespace std;
const int maxl = 1e6 + 7;
struct point {int x;int y;
};int n, ans;
point p[maxl];double dis(int a, int b) {return sqrt((p[a].x - p[b].x) * (p[a].x - p[b].x) + (p[a].y - p[b].y) * (p[a].y - p[b].y)) * 1.00;
}signed main(){cin >> n;for (int i = 1; i <= n; i++) cin >> p[i].x >> p[i].y;// 遍历所有点,并且要避免重复 for (int i = 1; i <= n; i++) {for (int j = 1; j < i; j++) {for (int k = 1; k < j; k++) {double a = dis(i, j);double b = dis(i, k);double c = dis(j, k);if (a + b > c && a + c > b && b + c > a)if ((a == b) || (a == c) || (b == c)) ans++;}}}cout << ans << endl;return 0;
}
试题 F: 删边问题
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
【问题描述】
给定一个包含 N 个结点 M 条边的无向图 G,结点编号 1 . . . N。其中每个
结点都有一个点权 W i _i i。
你可以从 M 条边中任选恰好一条边删除,如果剩下的图恰好包含 2 个连通
分量,就称这是一种合法的删除方案。
对于一种合法的删除方案,我们假设 2 个连通分量包含的点的权值之和分
别为 X 和 Y,请你找出一种使得 X 与 Y 的差值最小的方案。输出 X 与 Y 的差
值。
【输入格式】
第一行包含两个整数 N 和 M。
第二行包含 N 个整数,W 1 _1 1, W 2 _2 2. . . . W N _N N。
以下 M 行每行包含 2 个整数 U 和 V,代表结点 U 和 V 之间有一条边。
【输出格式】
一个整数代表最小的差值。如果不存在合法的删除方案,输出 −1。
【样例输入】
4 4
10 20 30 40
1 2
2 1
2 3
4 3
【样例输出】
20
【样例说明】
由于 1 和 2 之间实际有 2 条边,所以合法的删除方案有 2 种,分别是删除(2, 3) 之间的边和删除 (3, 4) 之间的边。
删除 (2, 3) 之间的边,剩下的图包含 2 个连通分量:{1, 2} 和 {3, 4},点权和分别是 30、70,差为 40。
删除 (3, 4) 之间的边,剩下的图包含 2 个连通分量:{1, 2, 3} 和 {4},点权和分别是 60、40,差为 20。
【评测用例规模与约定】
对于 20% 的数据,1 ≤ N, M ≤ 10000。
对于另外 20% 的数据,每个结点的度数不超过 2。
对于 100% 的数据,1 ≤ N, M ≤ 200000,0 ≤ W i _i i ≤ 109,1 ≤ U, V ≤ N。
作者思考
这个15分是真不好拿呀!真比后面两道20分的题还难!真无语😩
考察知识点:Tarjan 算法 缩点、Tarjan 算法 求割边、拓扑序
暴力点的解法,就是求完割边,遍历每个割边求差值。时间复杂度是O(M(u + v)) ≈ O(n 3 ^3 3),超时
优化,把他当有向图,然后进行缩点,缩点后会出现拓扑序,根据拓扑序,求节点值和。差值:所有节点值之和 - 2 * 其中一半连通节点和
题解
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 0x3f3f3f3f;
const int maxl = 1e6 + 7;
struct edge{int u;int v;bool operator < (edge b) const { // map 需要给出排序规则 if (u != b.u) return u < b.u;else return v < b.v;}
};int n, m, W, w[maxl], ans = MaxN;
/*
W ——所以节点值总和
w ——每个节点值
ans ——最小差值
*/// 无向图求割边
vector<int> G1[maxl];
vector<edge> e; // 求割边
map<edge, int> mp1; // 记录边数,标记掉重边,又可能是割边的边
int cnt1 = 1;
int dfn1[maxl], low1[maxl];
int flag1[maxl];// 有向图缩点,建新图。目的:利用新图拓扑序求节点值 和
vector<int> G2[maxl], nG[maxl]; // G2 ——有向图缩点,nG ——缩点后的新图
map<edge, int> mp2; // 新图建立会有重边
int tp;
stack<int> st;
int cnt2 = 1, sc;
int scc[maxl];
int flag2[maxl];
int dfn2[maxl], low2[maxl];
int nw[maxl], dp[maxl]; // nw ——缩点后的新权值,dp ——后i个点的权值和 void targan_bridge(int u, int fa) { // 求割边 dfn1[u] = low1[u] = cnt1++;for (int v : G1[u]) {if (!dfn1[v]) {targan_bridge(v, u);low1[u] = min(low1[u], low1[v]);if (low1[v] > dfn1[u]) e.push_back({min(u, v), max(u, v)});} else if (dfn1[v] < dfn1[u && v != fa]) low1[u] = min(low1[u], dfn1[v]);}
}void targan_point(int u) { // 缩点 st.push(u);flag2[u] = 1;dfn2[u] = low2[u] = cnt2++;for (int v : G2[u]) {if (!dfn2[v]) {targan_point(v);low2[u] = min(low2[u], low2[v]);} else if (flag2[v]) low2[u] = min(low2[u], dfn2[v]);}if (low2[u] == dfn2[u]) {sc++;do {tp = st.top();st.pop();scc[tp] = sc;flag2[tp] = 0;}while (tp != u);}
}signed main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> w[i];W += w[i]; }for (int i = 1, u, v; i <= m; i++) {cin >> u >> v;G1[u].push_back(v);G1[v].push_back(u);mp1[{min(u, v), max(u, v)}]++;G2[u].push_back(v);}int d = 0; // 判断给的图是否是个连通图for (int i = 1; i <= n; i++) {if (!dfn1[i]) {targan_bridge(i, i);d++;}if (!dfn2[i]) targan_point(i);} if (d > 1 || !e.size()) { // 不是连通图 或者 没有割边,直接返回 cout << -1 << endl;return 0;}// 缩点建新图for (int u = 1; u <= n; u++) {nw[scc[u]] += w[u];for (int v : G2[u]) {if (scc[v] != scc[u] && !mp2[{min(u, v), max(u, v)}]) {nG[scc[u]].push_back(scc[v]);mp2[{min(u, v), max(u, v)}]++; }}} // 根据拓扑序,求节点权值和 for (int u = sc; u; u--) {dp[u] += nw[u];for (int v : nG[u]) dp[v] += dp[u];}for (edge birdge : e) {if (mp1[birdge] > 1) continue; // 重边,不用更新 ans的值int p = max(scc[birdge.u], scc[birdge.v]); // 割边中序号较大的点int t = dp[p];ans = min(ans, abs(W - t - t)); // 计算差值 }cout << ans << endl; return 0;
}
试题 G: AB 路线
时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
【问题描述】
有一个由 N × M 个方格组成的迷宫,每个方格写有一个字母 A 或者 B。小蓝站在迷宫左上角的方格,目标是走到右下角的方格。他每一步可以移动到上下左右相邻的方格去。
由于特殊的原因,小蓝的路线必须先走 K 个 A 格子、再走 K 个 B 格子、再走 K 个 A 格子、再走 K 个 B 格子……如此反复交替。
请你计算小蓝最少需要走多少步,才能到达右下角方格?
注意路线经过的格子数不必一定是 K 的倍数,即最后一段 A 或 B 的格子可以不满 K 个。起点保证是 A 格子。
例如 K = 3 时,以下 3 种路线是合法的:
AA
AAAB
AAABBBAAABBB
以下 3 种路线不合法:
ABABAB
ABBBAAABBB
AAABBBBBBAAA
【输入格式】
第一行包含三个整数 N、M 和 K。
以下 N 行,每行包含 M 个字符(A 或 B),代表格子类型。
【输出格式】
一个整数,代表最少步数。如果无法到达右下角,输出 −1。
【样例输入】
4 4 2
AAAB
ABAB
BBAB
BAAA
【样例输出】
8
【样例说明】
每一步方向如下:下右下右上右下下;路线序列:AABBAABBA。
【评测用例规模与约定】
对于 20% 的数据,1 ≤ N, M ≤ 4。
对于另 20% 的数据,K = 1。
对于 100% 的数据,1 ≤ N, M ≤ 1000,1 ≤ K ≤ 10。
作者思考
这题其实不难,就是走迷宫加强版。让在下给您分析一下。
最短路
两种方法
- bfs、堆优化,步数最小
- dp[i][j] —— 当前步最小
附加条件 : - AB交错走,且A先走
- 每次走k步,最后一步,可以走少于k不
这个很好实现嘛,比如,bfs中节点结构体中加一个flag代表是谁走,cnt代表现在走了多少步,d代表方向。就直接可以实现了。🥳
这里给出比较巧妙的解决办法,不用设这么多变量。利用步数,直接看代码吧,不难的,就是很巧妙。👍
思路有很多,我就给出我的吧!
题解
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 0x3f3f3f3f;
const int maxl = 1e3 + 7;
struct node {int x, y;int step;
};
int dx[] = {0, 1, -1, 0, 0};
int dy[] = {0, 0, 0, 1, -1};int n, m, k;
char mp[maxl][maxl];
int dp[maxl][maxl];
node tp;
queue<node> q;int main(){memset(dp, 0x3f, sizeof(dp)); // 赋最大值cin >> n >> m >> k;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> mp[i][j];}} if (mp[1][1] != 'A') {cout << -1 << endl;return 0;}dp[1][1] = 0;q.push({1, 1, 0});while (!q.empty()) {tp = q.front();q.pop();int x = tp.x;int y = tp.y;int step = tp.step;for (int i = 1; i <= 4; i++) {int nx = x + dx[i];int ny = y + dy[i];int nstep = (step + 1) % (2 * k);if (nx < 1 || ny < 1 || nx > n || ny > m) continue;if (mp[nx][ny] == 'A' && nstep >= k) continue;if (mp[nx][ny] == 'B' && nstep < k) continue;if (dp[nx][ny] > dp[x][y] + 1) {dp[nx][ny] = dp[x][y] + 1;q.push({nx, ny, nstep});}}}if (dp[n][m] == MaxN) cout << -1 << endl;else cout << dp[n][m] << endl;return 0;
}
试题 H: 抓娃娃
时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
【问题描述】
小明拿了 n 条线段练习抓娃娃。他将所有线段铺在数轴上,第 i 条线段的左端点在 l i _i i,右端点在 r i _i i。小明用 m 个区间去框这些线段,第 i 个区间的范围是 [L i _i i, R i _i i]。如果一个线段有 至少一半 的长度被包含在某个区间内,则将其视为被这个区间框住。请计算出每个区间框住了多少个线段?
【输入格式】
输入共 n + m + 1 行。
第一行为两个正整数 n, m。
后面 n 行,每行两个整数 l i _i i,r i _i i。
后面 m 行,每行两个整数 L i _i i, R i _i i。
【输出格式】
输出共 m 行,每行一个整数。
【样例输入】
3 2
1 2
1 3
3 4
1 4
2 3
【样例输出】
3
2
【评测用例规模与约定】
对于 20% 的数据,保证 n, m ≤ 10 3 ^3 3。
对于 100% 的数据,保证 n, m ≤ 10 5 ^5 5,l i _i i < r i _i i,0 < l i _i i,r i _i i, L i _i i, R i _i i ≤ 10 6 ^6 6,max{r i _i i − l i _i i} ≤ min{R i _i i − L i _i i}
作者思考
我只能说,这道题是真的简单。而且是20分啊?!!为啥不放到最前面10分啊?真服了😡
不就是,最基础的前缀和与差分嘛!
抓住以下几个点:
- 框住区间中间,就算抓住
- 会有精度问题。乘2防止
题解
#include<bits/stdc++.h>
using namespace std;
const int maxl = 2e6 + 7;int n, m;
int sum[maxl]; int main(){cin >> n >> m;for (int i = 1, l, r; i <= n; i++) {cin >> l >> r;sum[l + r]++;}for (int i = 1; i < maxl; i++) sum[i] += sum[i - 1];for (int i = 1, l, r; i <= m; i++) {cin >> l >> r;l *= 2;r *= 2;cout << sum[r] - sum[l - 1] << endl;}return 0;
}
后面两道题,作者能力有限不会。如果你们能会的话。记得留言告诉我。在下把题目放在这里了。
试题 I: 拼数字
时间限制: 1.0s 内存限制: 256.0MB 本题总分:25 分
【问题描述】
小蓝要用 N 个数字 2 和 M 个数字 3 拼出一个 N + M 位的整数。请你计算
小蓝能拼出的最大的 2023 的倍数是多少?
【输入格式】
两个整数 N 和 M。
【输出格式】
一个 N + M 位的整数,代表答案。如果拼不出 2023 的倍数,输出 −1。
【样例输入】
2 8
【样例输出】
2233333333
【评测用例规模与约定】
对于 20% 的数据,1 ≤ N, M ≤ 12。
对于 40% 的数据,1 ≤ N, M ≤ 100。
对于 60% 的数据,1 ≤ N, M ≤ 10000。
对于 100% 的数据,1 ≤ N, M ≤ 1000000。
试题 J: 逃跑
时间限制: 1.0s 内存限制: 256.0MB 本题总分:25 分
【问题描述】
小明所在星系有 n 颗星球,编号为 1 到 n。这些星球通过 n − 1 条无向边连成一棵树。根结点为编号为 1 的星球。
为了在星际战争到来时逃到其他星系,小明在根结点设置了逃离用的传送门。每个星球的人只需要一直往父结点星球移动就可以抵达根结点。为了方便各个星球的人去往根结点,小明将其中 m 个星球设置为了跳板星球。在从某个星球去往根结点的路径上,当一个人经过任意星球(包括起点星球)时,他可以尝试直接跳跃到 其前往根结点路径上的除当前星球以外的第一个跳板星球,其时间花费和走到父结点星球的时间花费相同,都是 1 单位时间。
然而,因为技术问题,向跳板星球的跳跃并不一定成功,每一次跳跃都有p 的概率失败,并转而跳跃到当前星球的父结点星球(相当于直接走到父结点星球);同时此跳板星球失效,将 不再视为跳板星球。
为了衡量移动效率,小明想知道,如果一个人在这 n 颗星球中随机选择一颗出发前往根结点,其花费的最短时间的期望是多少单位时间?
【输入格式】
输入共 n + 1 行,第一行为两个正整数 n、m 和一个浮点数 p。
后面 n − 1 行,每行两个正整数 xi
, y i _i i 表示第 i 条边的两个端点。
最后一行,共 m 个正整数表示所有跳板星球的编号。
【输出格式】
一行,一个浮点数,表示答案(请保留两位小数)。
【样例输入】
4 1 0.2
1 2
2 3
3 4
2
【样例输出】
1.30
【样例说明】
从 1 号星球出发的时间花费为 0;
从 2 号星球出发的时间花费为 1;
从 3 号星球出发的时间花费为 2;
从 4 号星球出发的时间花费为 0.8 × 2 + 0.2 × 3 = 2.2。
所以期望时间为 (0+1+2+2.2)/4 = 1.3。
【评测用例规模与约定】
对于 30% 的数据,保证 1 ≤ n ≤ 2000。
对于 100% 的数据,保证 1 ≤ n ≤ 10 6 ^6 6 ,1 ≤ m ≤ n,0 < p < 1。
相关文章:

2023第十四届蓝桥杯国赛 C/C++ 大学 B 组
文章目录 前言试题 A: 子 2023作者思考题解答案 试题 B: 双子数作者思考题解 试题 C: 班级活动作者思考题解 试题 D: 合并数列作者思考题解 试题 E: 数三角作者思考题解 试题 F: 删边问题作者思考题解 试题 G: AB 路线作者思考题解 试题 H: 抓娃娃作者思考题解 试题 I: 拼数字试…...

如何在页面中加入百度地图
官方文档:jspopularGL | 百度地图API SDK (baidu.com) 添加一下代码就可以实现 <!DOCTYPE html> <html> <head><meta name"viewport" content"initial-scale1.0, user-scalableno"/><meta http-equiv"Conten…...

Windows VC++提升当前进程权限到管理员权限
Windows VC提升当前进程权限 Windows VC提升当前进程权限到管理员权限 Windows VC提升当前进程权限到管理员权限 有时候Windows下我们需要提升当前进程的权限到管理员权限,相关VC代码如下: #ifndef SAFE_CLOSE_HANDLE #define SAFE_CLOSE_HANDLE(handl…...
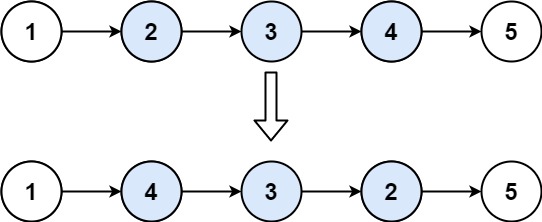
算法leetcode|92. 反转链表 II(rust重拳出击)
文章目录 92. 反转链表 II:样例 1:样例 2:提示:进阶: 分析:题解:rust:go:c:python:java: 92. 反转链表 II: 给你单链表的…...
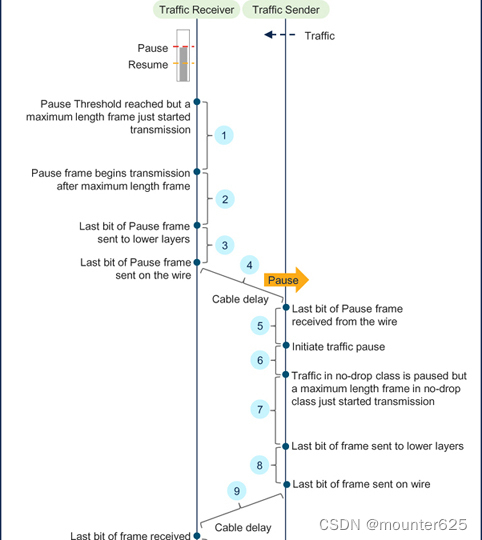
Chapter 7 - 3. Congestion Management in Ethernet Storage Networks以太网存储网络的拥塞管理
Pause Threshold for Long Distance Links长途链路的暂停阈值 This section uses the following basic concepts: 本节使用以下基本概念: Bit Time (BT): It is the time taken to transmit one bit. It is the reciprocal of the bit rate. For example, BT of a 10 GbE po…...
优雅玩转实验室服务器(二)传输文件
使用服务器最重要的肯定是传输文件了,我们不仅需要本地的一些资源上传到服务器,好进行实验,也需要将服务器计算得到的实验结果传输到本地,来进行预览或者报告撰写。 首先,由于涉及到服务器操作,我强烈推荐…...

动态面板简介以及ERP原型图案列
动态面板简介以及ERP原型图案列 1.Axure动态面板简介2.使用Axure制作ERP登录界面3.使用Asure完成左侧菜单栏4.使用Axuer完成公告栏5.使用Axuer完成左边侧边栏 1.Axure动态面板简介 在Axure RP中,动态面板是一种强大的交互设计工具,它允许你创建可交互的…...

漏刻有时百度地图API实战开发(12)(切片工具的使用、添加自定义图层TileLayer)
TileLayer向地图中添加自定义图层 var tileLayer new BMap.TileLayer();tileLayer.getTilesUrl function (tileCoord, zoom) {var x tileCoord.x;var y tileCoord.y;return images/tiles/ zoom /tile- x _ y .png;}var lockMap new BMap.MapType(lock_map, tileLaye…...

python 爬虫 m3u8 视频文件 加密解密 整合mp4
文章目录 一、完整代码二、视频分析1. 认识m3u8文件2. 获取密钥,构建解密器3. 下载ts文件4. 合并ts文件为mp4 三、总结 一、完整代码 完整代码如下: import requests from multiprocessing import Pool import re import os from tqdm import tqdm fro…...

mybatis中xml文件容易搞混的属性
目录 第一章、1.1)MyBatis中resultMap标签1.2)MyBatis的resultType1.3)MyBatis的parameterType1.4)type属性1.5)jdbcType属性1.6)javaType属性1.7)ofType属性 友情提醒: 先看文章目录ÿ…...

android Retrofit2.0请求 延长超时操作
import okhttp3.OkHttpClient; import retrofit2.Retrofit; import retrofit2.converter.gson.GsonConverterFactory;public class MyApiClient {private static final String BASE_URL "https://api.example.com/";// 创建 OkHttpClient,并设置超时时间…...

Axure之动态面板轮播图
目录 一.介绍 二.好处 三.动态面板轮播图 四.动态面板多方式登录 五.ERP登录 六.ERP的左侧菜单栏 七.ERP的公告栏 今天就到这了哦!!!希望能帮到你了哦!!! 一.介绍 Axure中的动态面板是一个非常有用的组…...
、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度)
一文读懂算法中的时间复杂度和空间复杂度,O(1)、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度
时间复杂度和空间复杂度是什么 时间复杂度(Time Complexity)是描述算法运行时间长短的一个度量。空间复杂度(Space Complexity)是描述算法在运行过程中所需要的存储空间大小的一个度量。 时间复杂度和空间复杂度是衡量算法性能…...
LWIP热插拔功能实现
0 工具准备 1.lwip 1.4.1 2.RTOS(本文使用rt-thread)1 使能连接变化回调功能 打开lwipopts.h,将宏定义LWIP_NETIF_LINK_CALLBACK的值设为1,如下: #define LWIP_NETIF_LINK_CALLBACK 1这个宏定义被使能后会将…...
android下的app性能测试应主要针对那些方面,如何开展?
如何开展安卓手机下的App性能测试,对于优秀的测试人员而言,除了要懂得性能测试的步骤流程外,还应该懂的性能测试的一些其他知识,比如性能测试指标、各指标的意义,常用的性能测试工具、如何查看结果分析等等知识。所以本…...
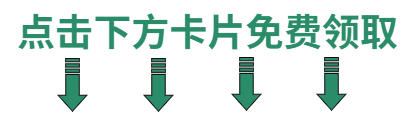
【深度学习】注意力机制(二)
本文介绍一些注意力机制的实现,包括EA/MHSA/SK/DA/EPSA。 【深度学习】注意力机制(一) 【深度学习】注意力机制(三) 目录 一、EA(External Attention) 二、Multi Head Self Attention 三、…...
学习黑马vue
项目分析 项目下载地址:vue-admin-template-master: 学习黑马vue 项目下载后没有环境可参考我的篇文章,算是比较详细:vue安装与配置-CSDN博客 安装这两个插件可格式化代码,vscode这个软件是免费的,官网:…...
gdb本地调试版本移植至ARM-Linux系统
移植ncurses库 本文使用的ncurses版本为ncurses-5.9.tar.gz 下载地址:https://ftp.gnu.org/gnu/ncurses/ncurses-5.9.tar.gz 1. 将ncurses压缩包拷贝至Linux主机或使用wget命令下载并解压 tar-zxvf ncurses-5.9.tar.gz 2. 解压后进入到ncurses-5.9目录…...
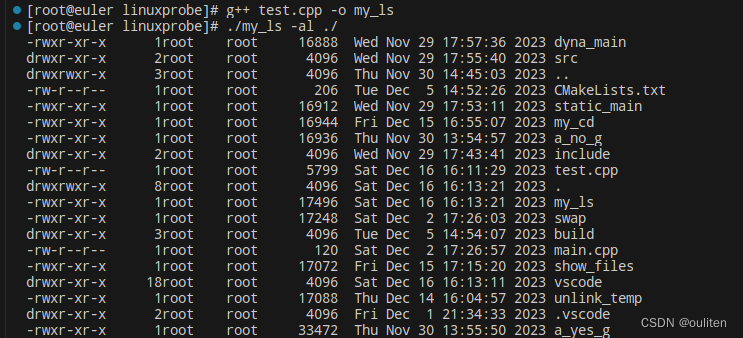
《Linux C编程实战》笔记:实现自己的ls命令
关键函数的功能及说明 1.void display_attribute(struct stat buf,char *name) 函数功能:打印文件名为name的文件信息,如 含义分别为:文件的类型和访问权限,文件的链接数,文件的所有者,文件所有者所属的组…...
Python个人代码随笔(观看无益,请跳过)
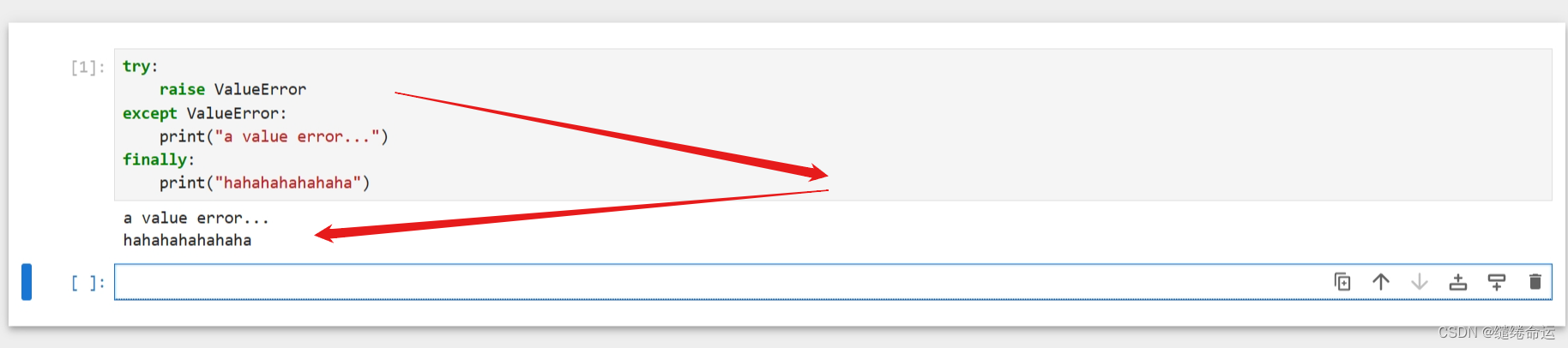
异常抛错:一般来说,在程序中,遇到异常时,会从这一层逐层往外抛错,一直抛到最外层,由最外层把错误显示在用户终端。 try:raise ValueError("A value error...") except ValueError:print("V…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
