【LeetCode: 2415. 反转二叉树的奇数层 | BFS + DFS】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |


🍔 目录
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ BFS | DFS
- 🥦 求解思路
- 🥦 实现代码 - BFS
- 🥦 运行结果
- 🥦 实现代码 - DFS
- 🥦 运行结果
- 💬 共勉
🚩 题目链接
- 2415. 反转二叉树的奇数层
⛲ 题目描述
给你一棵 完美 二叉树的根节点 root ,请你反转这棵树中每个 奇数 层的节点值。
例如,假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ,那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。
反转后,返回树的根节点。
完美 二叉树需满足:二叉树的所有父节点都有两个子节点,且所有叶子节点都在同一层。
节点的 层数 等于该节点到根节点之间的边数。
示例 1:
输入:root = [2,3,5,8,13,21,34]
输出:[2,5,3,8,13,21,34]
解释:
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ,反转后为 5、3 。
示例 2:
输入:root = [7,13,11]
输出:[7,11,13]
解释:
在第 1 层的节点分别是 13、11 ,反转后为 11、13 。
示例 3:
输入:root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出:[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释:奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ,反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ,反转后为 2、2、2、2、1、1、1、1 。
提示:
树中的节点数目在范围 [1, 214] 内
0 <= Node.val <= 105
root 是一棵 完美 二叉树
🌟 求解思路&实现代码&运行结果
⚡ BFS | DFS
🥦 求解思路
- 思路一:通过BFS求解,如果是奇数层,需要先将结果记录,然后进行反转即可。
- 思路二:通过DFS求解,如果是奇数层,交换节点的数值,然后递归交换root1的左子树和root2的右子树;同理,递归root1的右子树和root2的左子树。
- 实现代码如下所示:
🥦 实现代码 - BFS
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode reverseOddLevels(TreeNode root) {Queue<TreeNode> queue=new LinkedList<>();queue.add(root);int cnt=0;while(!queue.isEmpty()){int size=queue.size();List<TreeNode> list=new ArrayList<TreeNode>();for(int i=0;i<size;i++){TreeNode temp=queue.poll();if(cnt%2==1) list.add(temp);if(temp.left!=null){queue.add(temp.left);}if(temp.right!=null){queue.add(temp.right);}}if(cnt%2==1){for (int l=0,r=size-1;l<r;l++,r--) {int temp=list.get(l).val;list.get(l).val=list.get(r).val;list.get(r).val=temp;}}cnt++;}return root;}
}
🥦 运行结果
🥦 实现代码 - DFS
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode reverseOddLevels(TreeNode root) {dfs(root.left,root.right,1);return root;}public void dfs(TreeNode root1,TreeNode root2,int depth){if(root1==null||root2==null) return;if(depth%2==1){int temp=root1.val;root1.val=root2.val;root2.val=temp;}dfs(root1.left,root2.right,depth+1);dfs(root1.right,root2.left,depth+1);}
}
🥦 运行结果
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【LeetCode: 2415. 反转二叉树的奇数层 | BFS + DFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

期货股市联动(期股联动助推资本市场上扬)
期股联动——期货股市助推资本市场上扬 随着我国资本市场的不断发展,期货和股票这两个市场也在逐渐紧密地联系起来。期货和股票的相互作用是一种“期股联动”,它能够促进资本市场的上扬。 期货与股票市场 期货市场是一种标准化的场外交易市场…...

生成式AI的力量,释放RPA的无限潜能
回首即将过去的2023年,互联网行业似乎始终处在各种新概念的热潮激荡之中。其中,最引人注目的话题无疑是AI科技。自人工智能技术实现大规模突破以来,我们见证了一系列生成式AI的涌现。从ChatGPT到百度文心一言,它们纷纷登场&#x…...
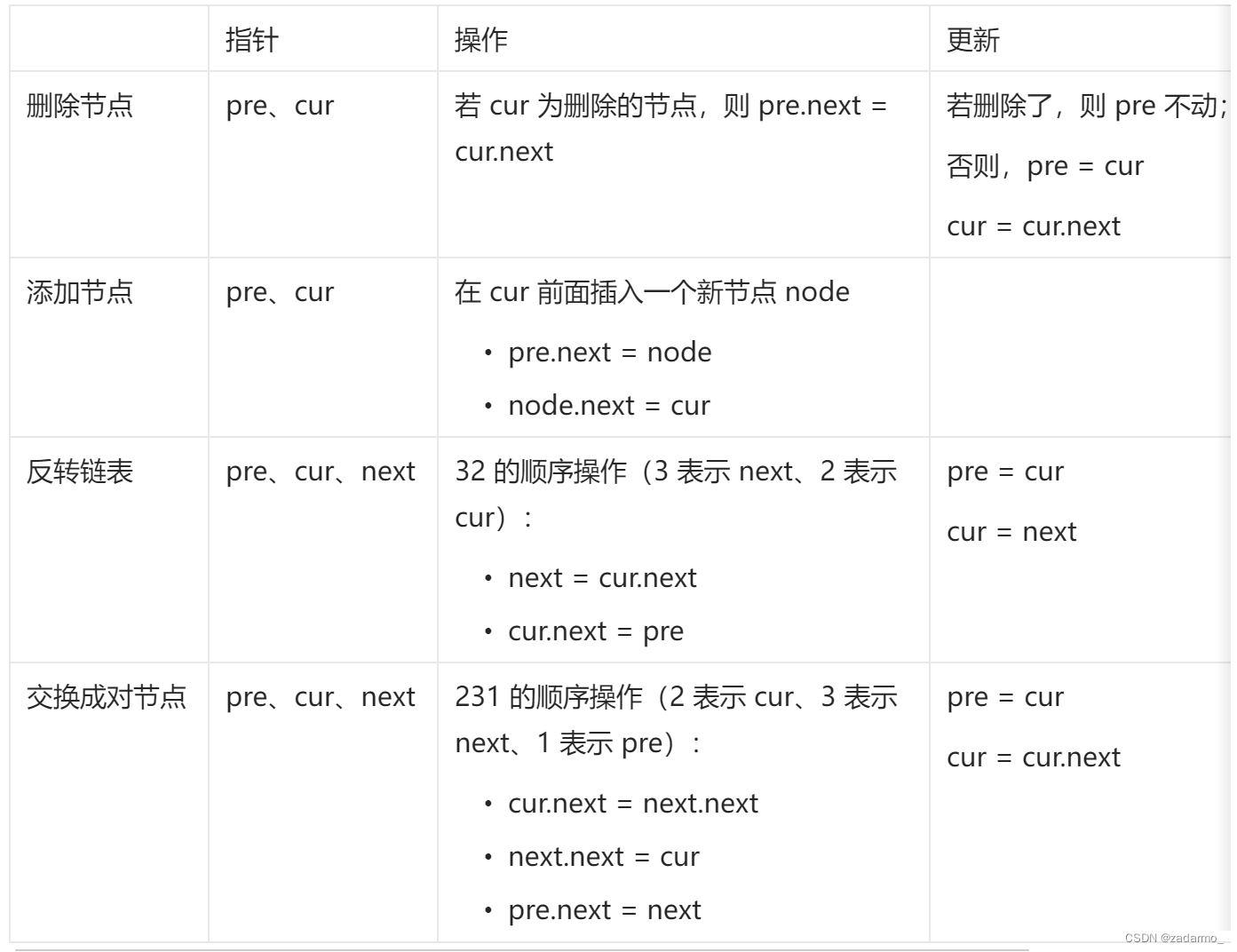
【leetcode】链表总结
说明:本文内容来自于代码随想录 链表基本操作 https://leetcode.cn/problems/design-linked-list/ 删除节点 https://leetcode.cn/problems/remove-linked-list-elements/description/,删除节点,虚拟头节点。定义两个节点,分别…...

焦虑,其实是你自愿选择的
如果一个人想要焦虑,他可以永远焦虑下去 从上学,到找工作,从买房到结婚生娃,他总是可以选择用自己的头脑去过度思考未来还没有发生的事情,从而让自己无限焦虑下去,直到生命终结。 我们的生命是存在于当下…...

4G无线工业级路由器在智能制造设备互联互通中的角色
随着工业技术的不断发展和进步,智能制造已经成为了现代制造业的重要趋势和发展方向。而在智能制造过程中,设备之间的互联互通是至关重要的一环。在这个过程中,4G无线工业级路由器扮演着重要的角色,它提供了稳定可靠的网络连接&…...
gitbash下载安装
参考教程 零、下载 官网地址 2.43.0win64 链接:https://pan.baidu.com/s/16urs_nmky7j20-qNzUTTkg 提取码:7jaq 一、安装 图标组件(Additional icons):选择是否创建桌面快捷方式;桌面浏览(Win…...
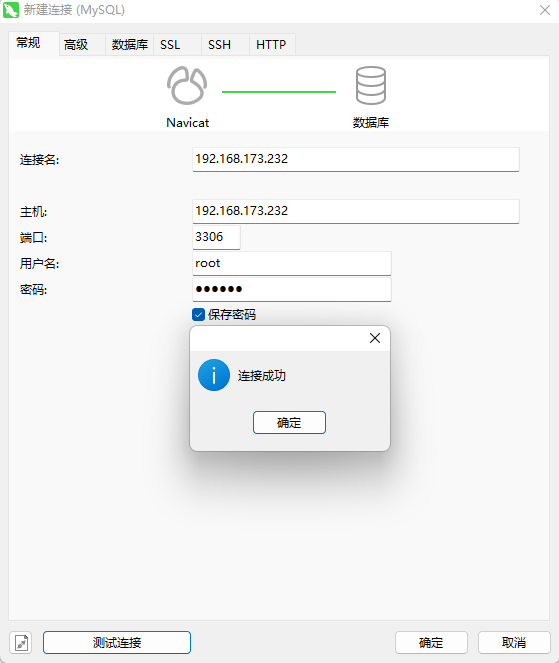
系列一、Linux中安装MySQL
一、Linux中安装MySQL 1.1、下载MySQL安装包 官网:https://dev.mysql.com/downloads/file/?id523327 我分享的: 链接:https://pan.baidu.com/s/188_9RnBYlWVzFb_UJH5aaQ?pwdyyds 提取码:yyds 1.2、上传至/opt目录 & 解压…...

开辟“护眼绿洲”,荣耀何以为师?
文 | 智能相对论 作者 | 佘凯文 俗话说,眼睛是心灵的窗户,可如今,人们对于这扇“窗户”的保护,似乎越来越不重视。 据人民日报今年发布的调查显示,中国眼病患病人数2.1亿,近视患者人数多达6亿࿰…...

Modbus RTU和Modbus TCP的区别 深入篇
目录 1 传输方式不同 2 硬件接口不同 3 校验码不同 4 指令内容不同 4.1 Modbus RTU 4.1.1 功能码为03,表示读寄存器 4.1.2 功能码为10,表示写多个寄存器 4.2 Modbus TCP 4.2.1 功能码为03,表示读寄存器 4.2.2 回复异常报文 5 传输速…...

【大数据】Doris 的集群规划和环境准备
Doris 的集群规划和环境准备 1.1 环境要求1.1 Linux 操作系统版本需求1.2 软件需求 1.2 硬件要求1.3 节点规划1.4 通信端口1.5 IP 地址绑定 Doris 作为一款开源的 MPP 架构 OLAP 数据库,能够运行在绝大多数主流的商用服务器上。为了能够充分运用 MPP 架构的并发优势…...
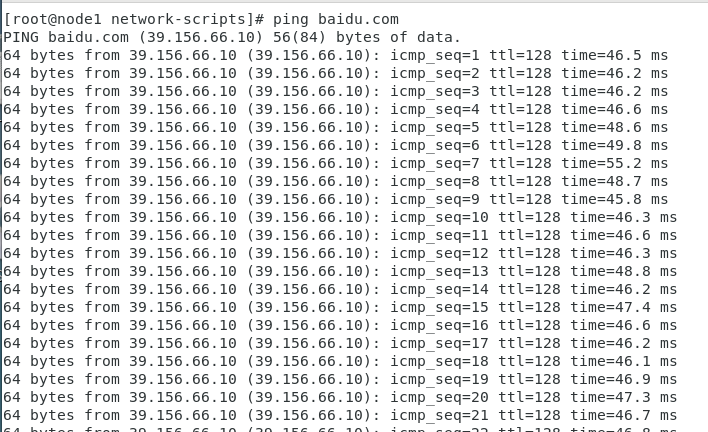
connect: Network is unreachable问题解决
第一步:查看ifcfg-ens33配置文件 cd /etc/sysconfig/network-scripts/ cat ifcfg-ens33 发现问题:GATEWAY写错成GATWAY 第二步:修改 vim ifcfg-ens33 第三步:检测是否成功 ping baidu.com 成功!...
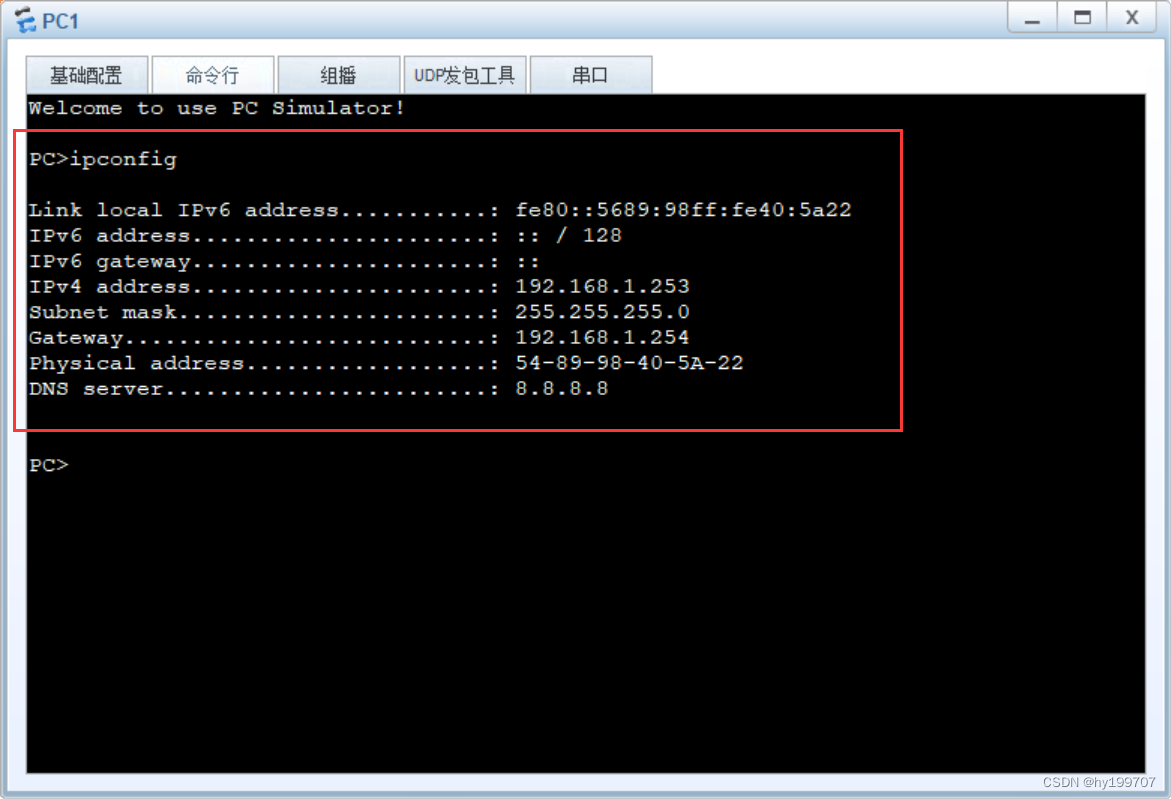
三层交换与DHCP
目录 一、三层交换 (一)基本概念 (二)转发原理 (三)ensp项目实验 二、DHCP (一)DHCP工作原理 1.DHCP的特点 2.工作原理 (二)DHCP项目实验 一、三层交…...

02markdown-学习笔记
一级标题 二级标题 三级标题 四级标题 五级标题 六级标题 换行符<br>标签 写入一段测试用的正文第二段测试文本,如果要对文本进行换行可以使用<br>标签 文本修饰符 字体为斜体的修饰,一对星号包含 字符为粗体,两对星号包含 字体为…...
UE5 动画 Sequencer-学习笔记
P2. 课程介绍 资料:https://www.bilibili.com/video/BV1Ag411873f?p2&vd_source707ec8983cc32e6e065d5496a7f79ee6 Sequencer不仅可以做互动动画,还可以导出视频与序列帧 P3-4. 界面介绍 https://www.bilibili.com/video/BV1Ag411873f?p3&spm_…...
visual studio code 好用的插件
vscode-icons Better comments 该插件对不同类型的注释会附加了不同的颜色,更加方便区分,帮助我们在代码中创建更人性化的注释。 Error Lens Error Lens插件是一款可以检测你编写的代码的语法错误,并且会显示出对语法错误的诊断信息…...
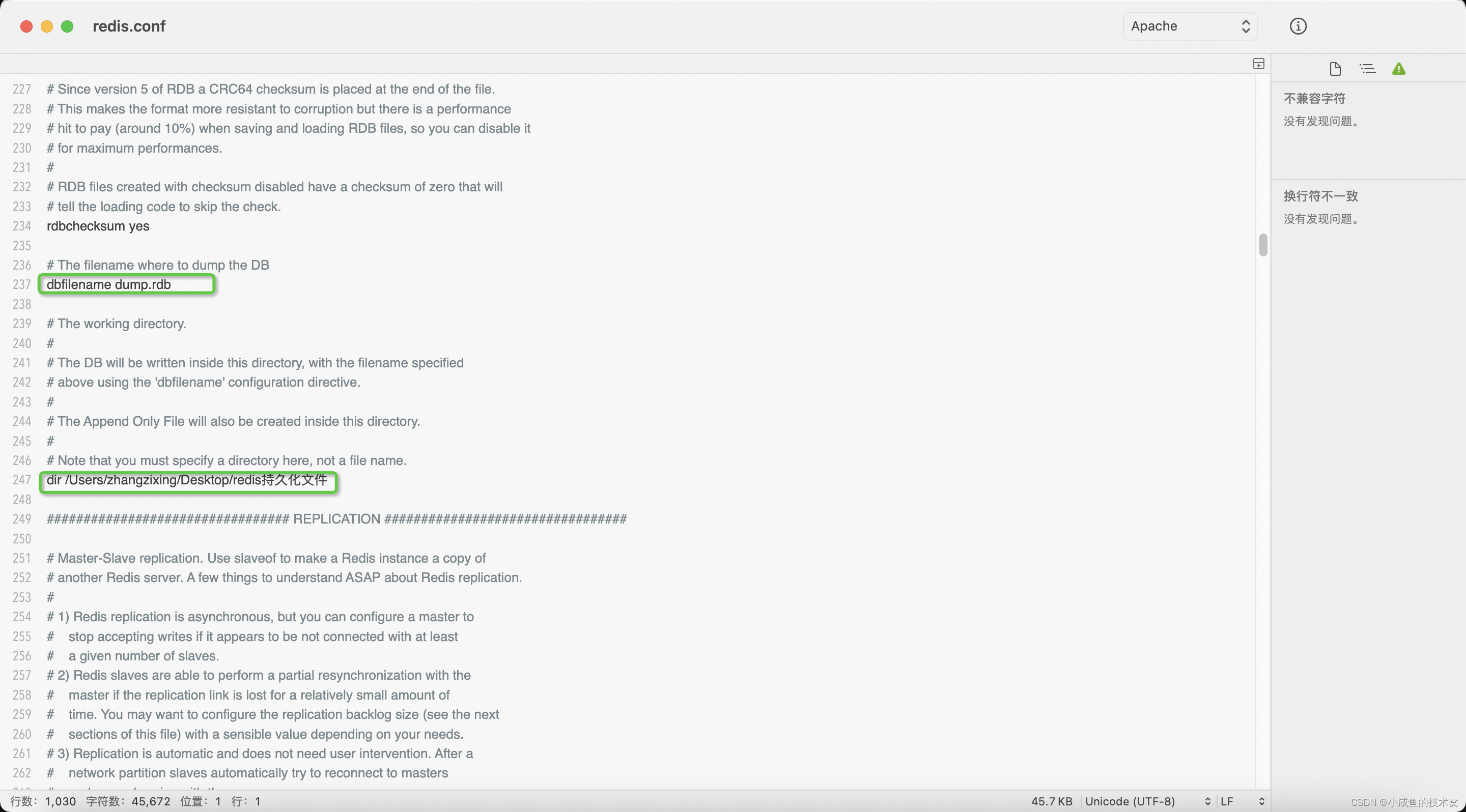
Redis 过期删除策略、内存回收策略、单线程理解
不知从何开始Redis的内存淘汰策略也开始被人问及,卷!真的是太卷了。难不成要我们去阅读Redis源码吗,其实问题的答案,在Redis中的配置文件中全有,不需要你阅读源码、这个东西就是个老八股,估计问这个东西是想…...

oracle 如何把数据库 date 日期格式 的数据 改成 2021-01-27
如果您要将日期"27-12月-29"更改为"2021-01-27"格式,您可以使用Oracle的日期格式化函数和字符串替换函数来实现。 以下是一个示例SQL语句,将日期"27-12月-29"更改为"2021-01-27"格式: sql UPDATE…...

Git 使用教程(超级详细)
目录 一:Git二:SVN与Git的的区别三、安装Git四:常规操作五:远程仓库六:创建与合并分支七:bug分支八:多人协作九:git可视化工具 Git Git 是一种分布式版本控制系统,用于…...
动态规划习题
动态规划的核心思想是利用子问题的解来构建整个问题的解。为此,我们通常使用一个表格或数组来存储子问题的解,以便在需要时进行查找和使用。 1.最大字段和 #include <iostream> using namespace std; #define M 200000int main() {int n, a[M], d…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
