01--二分查找
一. 初识算法
1.1 什么是算法?
在数学和计算机科学领域,算法是一系列有限的严谨指令,通常用于解决一类特定问题或执行计算
不正式的说,算法就是任何定义优良的计算过程:接收一些值作为输入,在有限的时间内,产生一些值作为输出。
1.2 什么是数据结构?
在计算机科学领域,数据结构是一种数据组织、管理和存储格式,通常被选择用来高效访问数据
数据结构是一种存储和组织数据的方式,旨在便于访问和修改
1.3 衡量算法好坏
一般从以下维度来评估算法的优劣:正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)。
时间复杂度(time complexity):估算程序指令的执行次数(执行时间)。
空间复杂度(space complexity):估算所需占用的存储空间。
1.3.1 时间复杂度
常见的时间复杂度从快到慢:
常数复杂度 O(1)
对数复杂度 O(logn)
线性时间复杂度 O(n)
线性对数复杂度 O(nlogn)
平方 O(
)
立方 O(
)
指数 O(
)
阶乘 O(n!)
1.3.2 空间复杂度
空间复杂度就是算法需要多少内存,占用了多少空间
常用的空间复杂度有O(1)、O(n)、O()
二、二分查找
二分查找算法也称折半查找,是一种非常高效的工作于有序数组的查找算法。
2.1 二分查找基础版


/*** @description: 二分查找基础版* @author: 憨憨浩浩* @date: 2023/12/11 21:54* @param: [a, target]* @return: int**/public static int binarySearchBasic(int[] a, int target) {// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length - 1;// 当 i > j 时退出循环while (i <= j){// 定义中间指针int m = (i + j) / 2;if (a[m] > target){ // 目标值在左边j = m - 1;}else if (a[m] < target){ // 目标值在右边i = m + 1;}else { // 找到目标值返回对应索引return m;}}return -1; // 找不到目标值返回-1}
(i + j) / 2 有没有问题?
有问题,当数组长度足够长是会发生问题;
@Testpublic void Test01(){int i = Integer.MAX_VALUE / 2;int j = Integer.MAX_VALUE;int m = (i + j) / 2;System.out.println(m); // -536870913}解决方案:
@Testpublic void Test02(){int i = Integer.MAX_VALUE / 2;int j = Integer.MAX_VALUE;int m = (i + j) >>> 2;System.out.println(m); // 805306367}2.2 二分查找改变版
另一种写法
/*** @description: 二分查找改变版* @author: 憨憨浩浩* @date: 2023/12/11 22:10* @param: [a, target]* @return: int**/public static int binarySearchAlternative(int[] a,int target){// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length;// 当 i = j 时退出循环while (i < j){// 定义中间指针int m = (i + j) /2;if (a[m] > target){ // 目标值在左边j = m;} else if (a[m] < target) { // 目标值在右边i = m + 1;}else { // 找到目标值返回对应索引return m;}}return -1; // 找不到目标值返回-1}
2.3 二分查找性能

2.4 二分查找平衡版
/*** @description: 二分查找平衡版* @author: 憨憨浩浩* @date: 2023/12/13 13:46* @param: [a, target]* @return: int**/public static int binarySearchBalance(int[] a,int target){// 定义左侧指针int i = 0;// 定义右侧指针int j = a.length;// 当 i + 1 > j 时退出循环while (1 < j - i) {// 定义中间指针int m = (i + j) >>> 1;if (target < a[m]) { // 目标值在左边j = m;} else {i = m;}}// 查到返回i,查不到返回-1return (a[i] == target) ? i : -1;}
2.5 二分查找 Java 版
Java8源码:

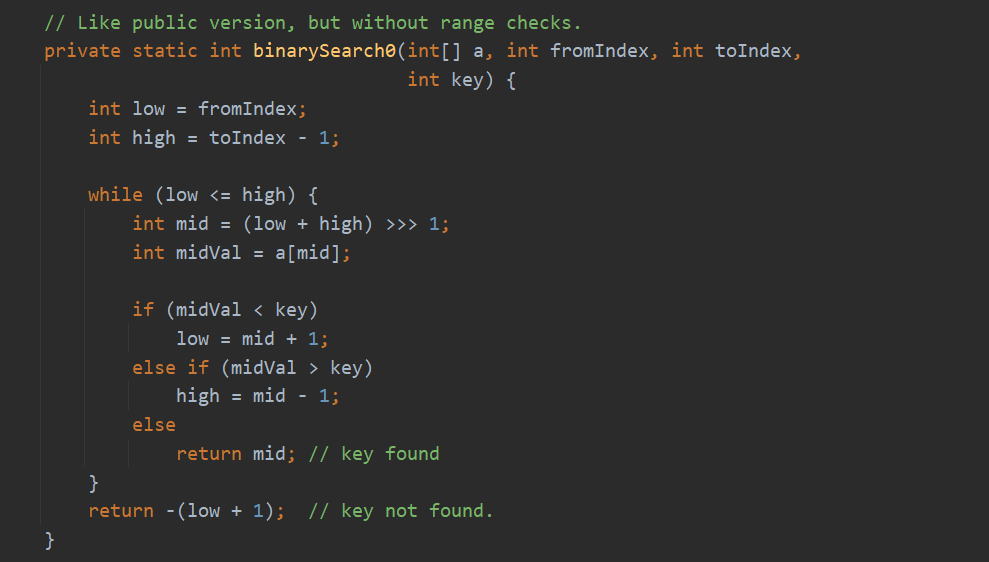
public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}private static int binarySearch0(int[] a, int fromIndex, int toIndex, int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.}
2.6 Leftmost 与 Rightmost

/*** @description: 二分查找返回左侧的索引值* @author: 憨憨浩浩* @date: 2023/12/15 20:21* @param: [a, target]* @return: int**/public static int binarySearchLeftmost1(int[] a,int target){int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置j = m - 1; // 继续向左}}return candidate;}如果希望返回的是最右侧元素
/*** @description: 二分查找返回最右侧值的索引* @author: 憨憨浩浩* @date: 2023/12/15 20:23* @param: [a, target]* @return: int**/public static int binarySearchRightmost1(int[] a,int target){int i = 0, j = a.length - 1;int candidate = -1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {candidate = m; // 记录候选位置i = m + 1; // 继续向右}}return candidate;}应用
对于 Leftmost 与 Rightmost,可以返回一个比 -1 更有用的值
Leftmost 改为
public static int binarySearchLeftmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target <= a[m]) {j = m - 1;} else {i = m + 1;}}return i;
}
Rightmost 改为
public static int binarySearchRightmost(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else {i = m + 1;}}return i - 1;
}大于等于中间值,都要向右找
几个名词
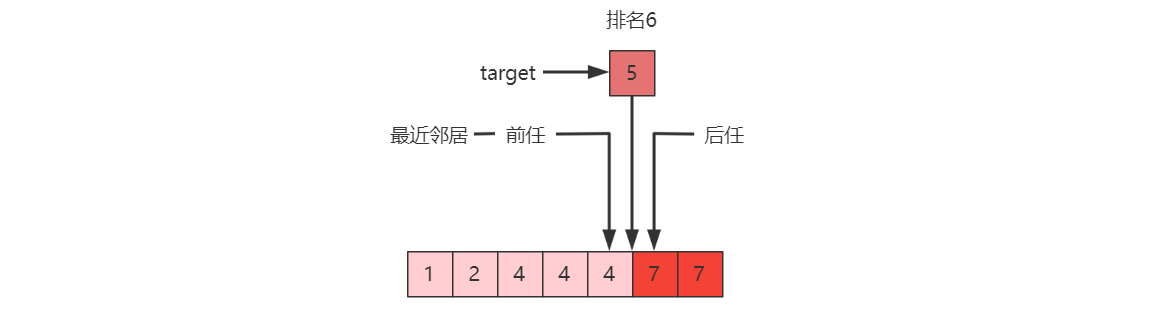


相关文章:

01--二分查找
一. 初识算法 1.1 什么是算法? 在数学和计算机科学领域,算法是一系列有限的严谨指令,通常用于解决一类特定问题或执行计算 不正式的说,算法就是任何定义优良的计算过程:接收一些值作为输入,在有限的时间…...

初识大数据应用,一文掌握大数据知识文集(1)
文章目录 🏆初识大数据应用知识🔎一、初识大数据应用知识(1)🍁 01、请用Java实现非递归二分查询?🍁 02、是客户端还是Namenode决定输入的分片?🍁 03、mapred.job.tracker命令的作用?…...
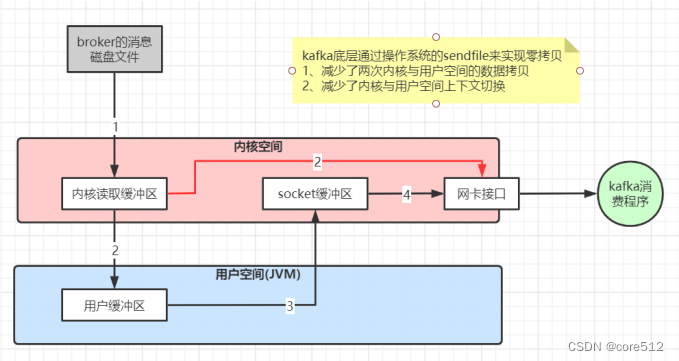
Kafka生产问题总结及性能优化实践
1、消息丢失情况 消息发送端: (1)acks0: 表示producer不需要等待任何broker确认收到消息的回复,就可以继续发送下一条消息。性能最高,但是最容易丢消息。大数据统计报表场景,对性能要求很高&am…...

[MySQL]数据库原理2,Server,DataBase,Connection,latin1、UTF-8,gb2312,Encoding,Default Collation——喵喵期末不挂科
希望你开心,希望你健康,希望你幸福,希望你点赞! 最后的最后,关注喵,关注喵,关注喵,佬佬会看到更多有趣的博客哦!!! 喵喵喵,你对我真的…...

【算法集训】基础数据结构:十、矩阵
矩阵其实就是二维数组,这些题目在9日集训中已经做过,这里做的方法大致相同。 第一题 1351. 统计有序矩阵中的负数 int countNegatives(int** grid, int gridSize, int* gridColSize) {int r gridSize;int c gridColSize[0];int ret 0;for(int i 0;…...

python排序算法 直接插入排序法和折半插入排序法
最近需要使用到一些排序算法,今天主要使针对直接插入排序和折半插入排序进行讲解。 首先是直接插入排序,其排序过程主要是,针对A[a1,a2,a3,a4,a5....an],从排序的序列头部起始位置开始,将其也就是a1视为只有一个元素的…...

【flutter对抗】blutter使用+ACTF习题
最新的能很好反编译flutter程序的项目 1、安装 git clone https://github.com/worawit/blutter --depth1 然后我直接将对应的两个压缩包下载下来(通过浏览器手动下载) 不再通过python的代码来下载,之前一直卡在这个地方。 如果读者可以正…...

OpenHarmony 如何去除系统锁屏应用
前言 OpenHarmony源码版本:4.0release / 3.2 release 开发板:DAYU / rk3568 一、3.2版本去除锁屏应用 在源码根目录下:productdefine/common/inherit/rich.json 中删除screenlock_mgr组件的编译配置,在rich.json文件中搜索th…...

Python - 搭建 Flask 服务实现图像、视频修复需求
目录 一.引言 二.服务构建 1.主函数 upload_gif 2.文件接收 3.专属目录 4.图像修复 5.gif2mp4 6.mp42gif 7.图像返回 三.服务测试 1.服务启动 2.服务调用 四.总结 一.引言 前面我们介绍了如何使用 Real-ESRGAN 进行图像增强并在原始格式 jpeg、jpg、mp4 的基础上…...

C#基础——构造函数、析构函数
C#基础——构造函数、析构函数 1、构造函数 构造函数是一种特殊的方法,用于在创建类的实例时进行初始化操作。构造函数与类同名,并且没有返回类型。 构造函数在对象创建时自动调用,可以用来设置对象的初始状态、分配内存、初始化字段等操作…...

jmeter 如何循环使用接口返回的多值?
有同学在用jmeter做接口测试的时候,经常会遇到这样一种情况: 就是一个接口请求返回了多个值,然后下一个接口想循环使用前一个接口的返回值。 这种要怎么做呢? 有一定基础的人,可能第一反应就是先提取前一个接口返回…...

VLAN 详解一(VLAN 基本原理及 VLAN 划分原则)
VLAN 详解一(VLAN 基本原理及 VLAN 划分原则) 在早期的交换网络中,网络中只有 PC、终端和交换机,当某台主机发送一个广播帧或未知单播帧时,该数据帧会被泛洪,甚至传递到整个广播域。而广播域越大ÿ…...

Android - 分区存储 MediaStore、SAF
官方页面 参考文章 一、概念 分区存储(Scoped Storage)的推出是针对 APP 访问外部存储的行为(乱建乱获取文件和文件夹)进行规范和限制,以减少混乱使得用户能更好的控制自己的文件。 公有目录被分为两大类:…...

Shiro框架权限控制
首先去通过配置类的用户认证,在用户认证完成后,进行用户授权,用户通过授权之后再跳转其他的界面时,会进行一个验证,当前账号是否有权限。 前端权限控制显示的原理 在前端中,通常使用用户的角色或权限信息来…...
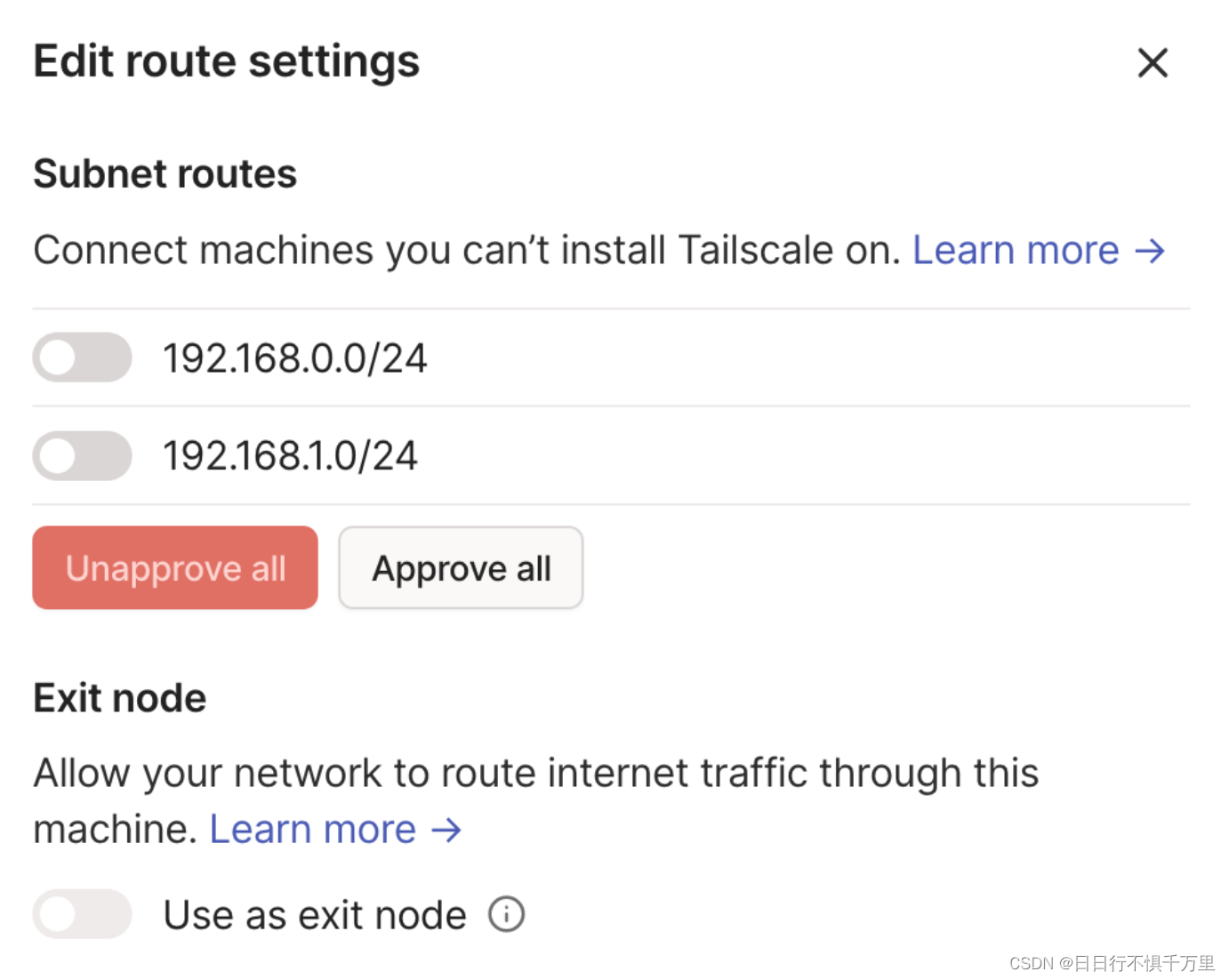
centOS7 安装tailscale并启用子网路由
1、在centOS7上安装Tailscale客户端 #安装命令所在官网位置:https://tailscale.com/download/linux #具体命令为: curl -fsSL https://tailscale.com/install.sh | sh #命令执行后如下图所示2、设置允许IP转发和IP伪装。 安装后,您可以启动…...

spring 项目中如何处理跨越cors问题
1.使用 CrossOrigin 注解 作用于controller 方法上 示例如下 RestController RequestMapping("/account") public class AccountController {CrossOriginGetMapping("/{id}")public Account retrieve(PathVariable Long id) {// ...}DeleteMapping(&quo…...

importlib --- import 的实现
3.1 新版功能. 源代码 Lib/importlib/__init__.py 概述 importlib 包具有三重目标。 一是在 Python 源代码中提供 import 语句的实现(并且因此而扩展 __import__() 函数)。 这提供了一个可移植到任何 Python 解释器的 import 实现。 与使用 Python 以…...

【PyTorch】现代卷积神经网络
文章目录 1. 理论介绍1.1. 深度卷积神经网络(AlexNet)1.1.1. 概述1.1.2. 模型设计 1.2. 使用块的网络(VGG)1.3. 网络中的网络(NiN)1.4. 含并行连结的网络(GoogLeNet)1.5. 批量规范化…...

用python编写九九乘法表
1 问题 我们在学习一门语言的过程中,都会练习到编写九九乘法表这个代码,下面介绍如何编写九九乘法表的流程。 2 方法 (1)打开pycharm集成开发环境,创建一个python文件,并编写第一行代码,主要构建…...
Google Gemini 模型本地可视化
Google近期发布了Gemini模型,而且开放了Gemini Pro API,Gemini Pro 可免费使用! Gemini Pro支持全球180个国家的38种语言,目前接受文本、图片作为输入并生成文本作为输出。 Gemini Pro的表现超越了其他同类模型,当前版…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
