CSS BFC详解
概念
BFC(Block Formatting Context)是CSS中的一个概念,用于描述一个独立的渲染区域,其中的元素按照一定规则进行布局和渲染。
BFC具有以下特性和作用
清除浮动:当一个元素的float属性设置为left或right时,会创建一个BFC,使得该元素不会被浮动元素覆盖。
阻止垂直外边距重叠:在同一个BFC中,相邻的两个块级元素的垂直外边距会发生重叠。但是在不同的BFC中,垂直外边距不会重叠。
自适应两栏布局:通过创建两个相邻的块级元素,并将其中一个设置为浮动或者使用绝对定位,可以实现自适应两栏布局。
防止文字环绕:当一个元素设置为浮动时,它会创建一个BFC,并且其他内容不会环绕在该浮动元素周围。
防止父元素高度塌陷:当父元素包含了浮动或者绝对定位的子元素时,如果没有清除浮动或者创建BFC,父元素的高度将塌陷为0。
创建BFC的条件
-
根元素()或包含根元素的元素。
-
浮动元素(float属性不为none)。
-
绝对定位元素(position为absolute或fixed)。
-
行内块元素(display为inline-block)。
-
表格单元格(display为table-cell,HTML表格单元格默认会创建BFC)。
-
overflow属性的值不为visible的块级元素。
BFC的布局规则
-
BFC中的块级盒子会垂直排列,从上到下。
-
相邻的块级盒子的垂直外边距会发生重叠,但是在不同的BFC中不会发生重叠。
-
BFC中的浮动盒子会参与计算高度,使得父元素能够包含浮动盒子。
-
BFC中的块级盒子在水平方向上不会溢出其包含块,而是会自动缩小宽度以适应包含块。
总结
BFC是一种布局上下文,可以解决一些常见的布局问题,并且具有一些特性和作用。通过合理地创建和利用BFC,可以更好地控制页面布局和渲染效果。
相关文章:

CSS BFC详解
概念 BFC(Block Formatting Context)是CSS中的一个概念,用于描述一个独立的渲染区域,其中的元素按照一定规则进行布局和渲染。 BFC具有以下特性和作用 清除浮动:当一个元素的float属性设置为left或right时ÿ…...
【C语言】实战项目——通讯录
引言 学会创建一个通讯录,对过往知识进行加深和巩固。 文章很长,要耐心学完哦! ✨ 猪巴戒:个人主页✨ 所属专栏:《C语言进阶》 🎈跟着猪巴戒,一起学习C语言🎈 目录 引言 实战 建…...

05 Rust 结构体
结构体 Rust 中的结构体(Struct)与元组(Tuple)都可以将若干个类型不一定相同的数据捆绑在一起形成整体,但结构体的每个成员和其本身都有一个名字,这样访问它成员的时候就不用记住下标了。 元组常用于非定…...
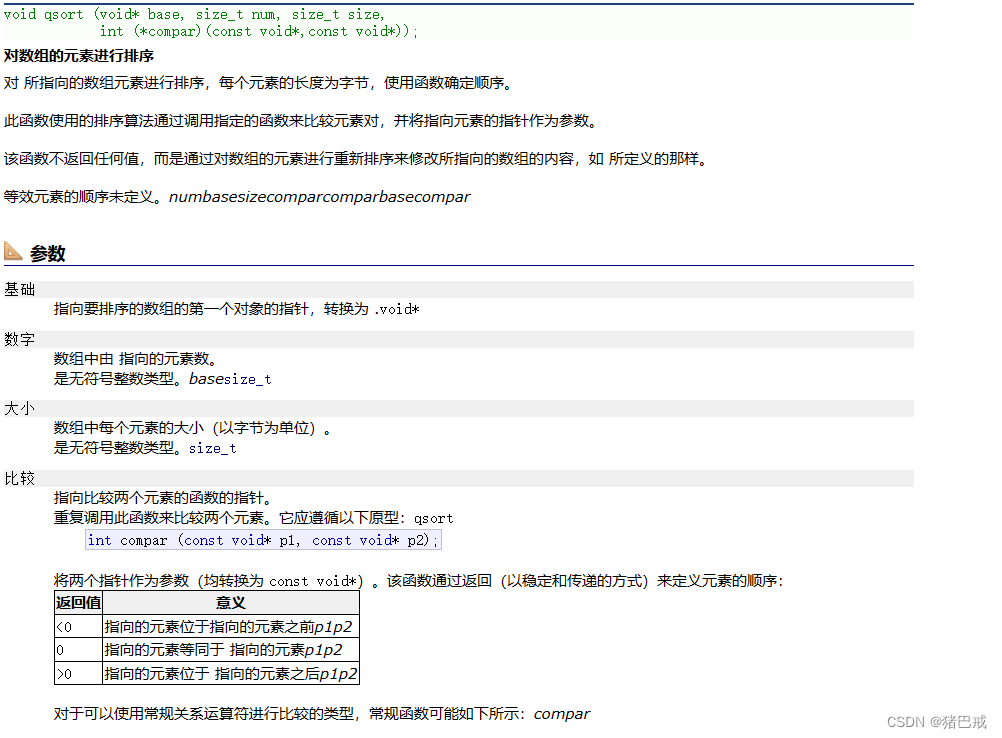
C语言预处理详解及其指令
预处理详解 1.预定义符号2.#define定义常量基本使用方法举例子如果在define定义的表示符后面加上分号会发生什么?用一下来解释 3. #define定义宏举例例1例2 4. 带有副作用的宏参数例如: 5. 宏替换的规则6. 宏函数的对比宏和函数的一个对比 7. #和##7.1 #运算符7.2 #…...
【数据结构—队列的实现】
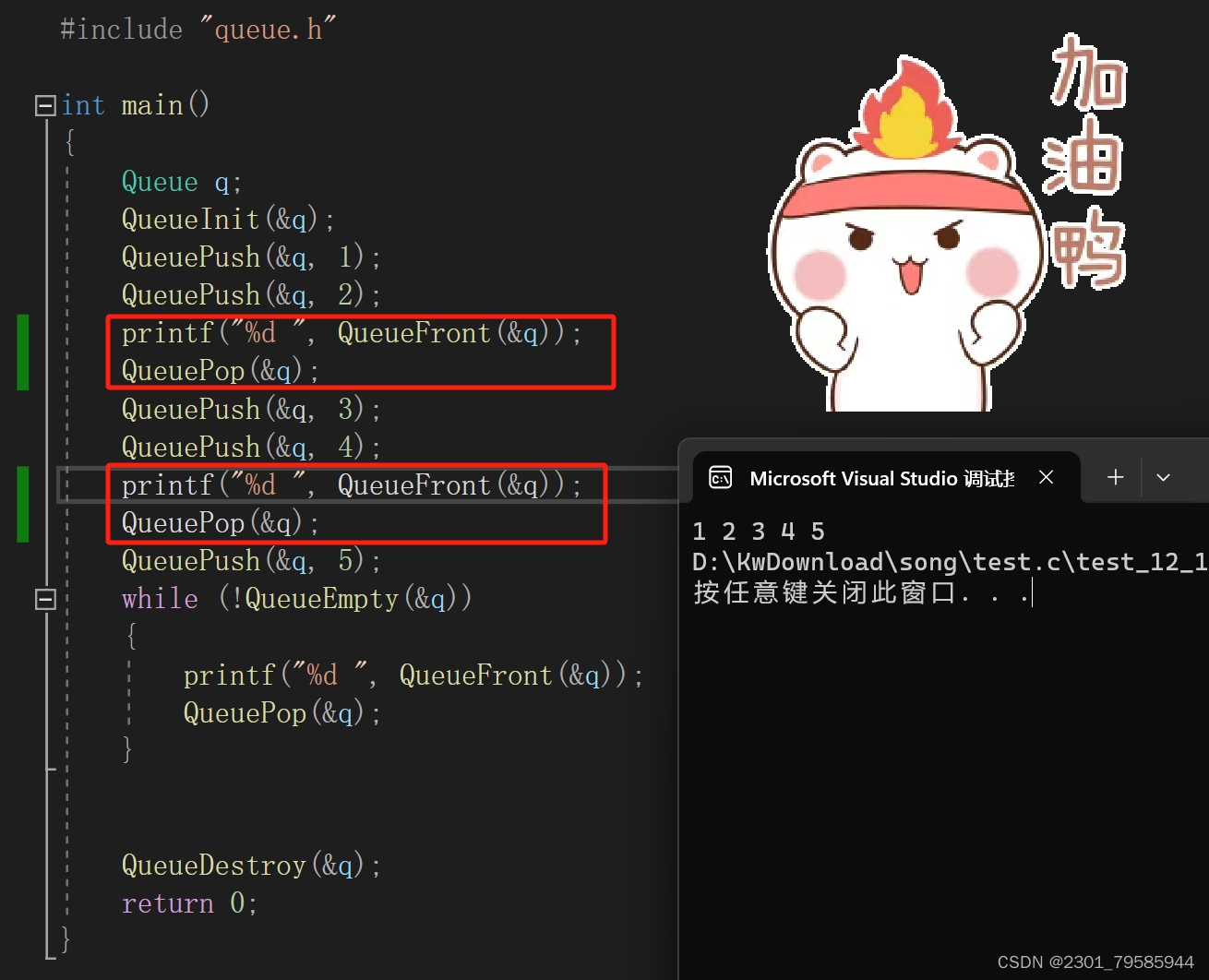
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、队列 1.1队列的概念及结构 二、队列的实现 2.1头文件的实现—Queue.h 2.2源文件的实现—Queue.c 2.3源文件的测试—test.c 三、测试队列实际数据的展示 3.…...
ASP.NET MVC实战之权限拦截Authorize使用
1,具体的实现方法代码如下 public class CustomAuthorizeAttribute : FilterAttribute, IAuthorizationFilter{/// <summary>/// 如果需要验证权限的时候,就执行进来/// </summary>/// <param name"filterContext"></par…...

java8实战 lambda表达式和函数式接口(上)
前言: 本博客对java8实战第三章的总结,也是上一篇博客行为化参数的延续,介绍一下函数式接口 Lambda表达式 lambda的表达式的结构由:参数,箭头,主体构成。 lambda示例 函数式接口: 先看上一篇…...
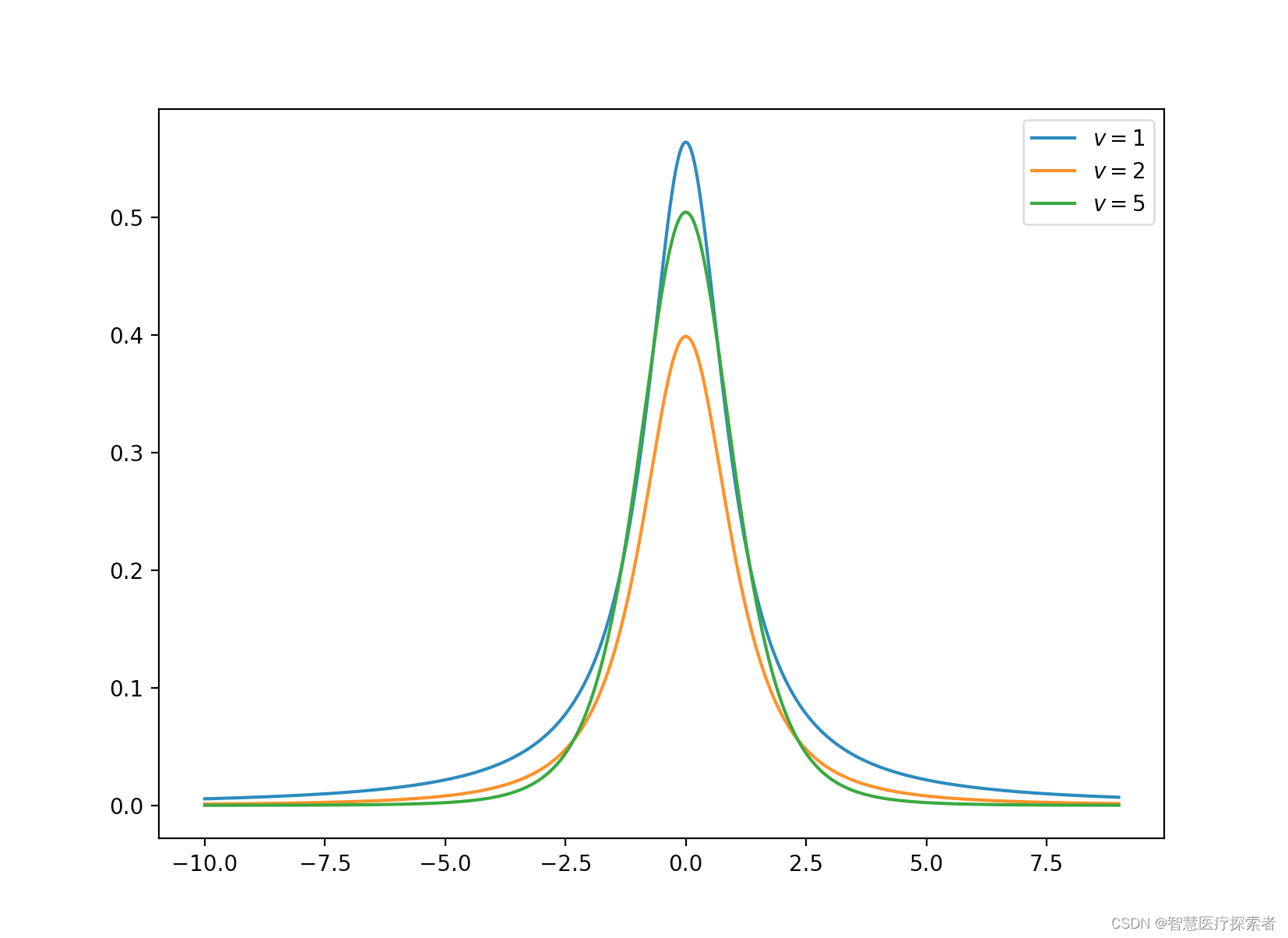
深度学习中的13种概率分布
1 概率分布概述 共轭意味着它有共轭分布的关系。 在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。 多…...

C#基础知识 - 操作数与运算符篇2
C#基础知识 - 操作数与运算符篇 4.2 运算符4.2.1 按操作数个数分类4.2.2 按运算类型分类4.2.3 对运算符 、-- 的使用4.2.4 关系运算符:>、 < 、> 、<、 ! 、4.2.5 逻辑运算符:&& || ! ^ & |4.2.6 位运算符:~ 、^、 &…...
第十五章总结
一.输入/输出流 1.输入流 InputStrema类是字节输入流的抽象类,它是所有字节输入流的父类。 该类中所有方法遇到错误都会引发IOException异常。 read()方法:从输入流中读取数据的下一个字节。返回0~255的int字节值。如果因为已经到达流末尾而没有可用的…...

音频I2S
前言 基于网上资料对相关概念做整理汇总,部分内容引用自文后文章。 学习目标:简单了解相关概念、相关协议。 1 概述 数字音频接口DAI,即Digital Audio Interfaces,顾名思义,DAI表示在板级或板间传输数字音频信…...

小程序中的合法域名的作用及条件有哪些?
小程序的合法域名是指小程序项目中使用的各种接口、资源文件等所在的域名。在小程序开发中,需要将这些域名添加到小程序后台的“开发设置”-“服务器域名”中进行配置,才能够正常使用。 合法域名的作用: 1.作为小程序请求的 API 服务器域名…...
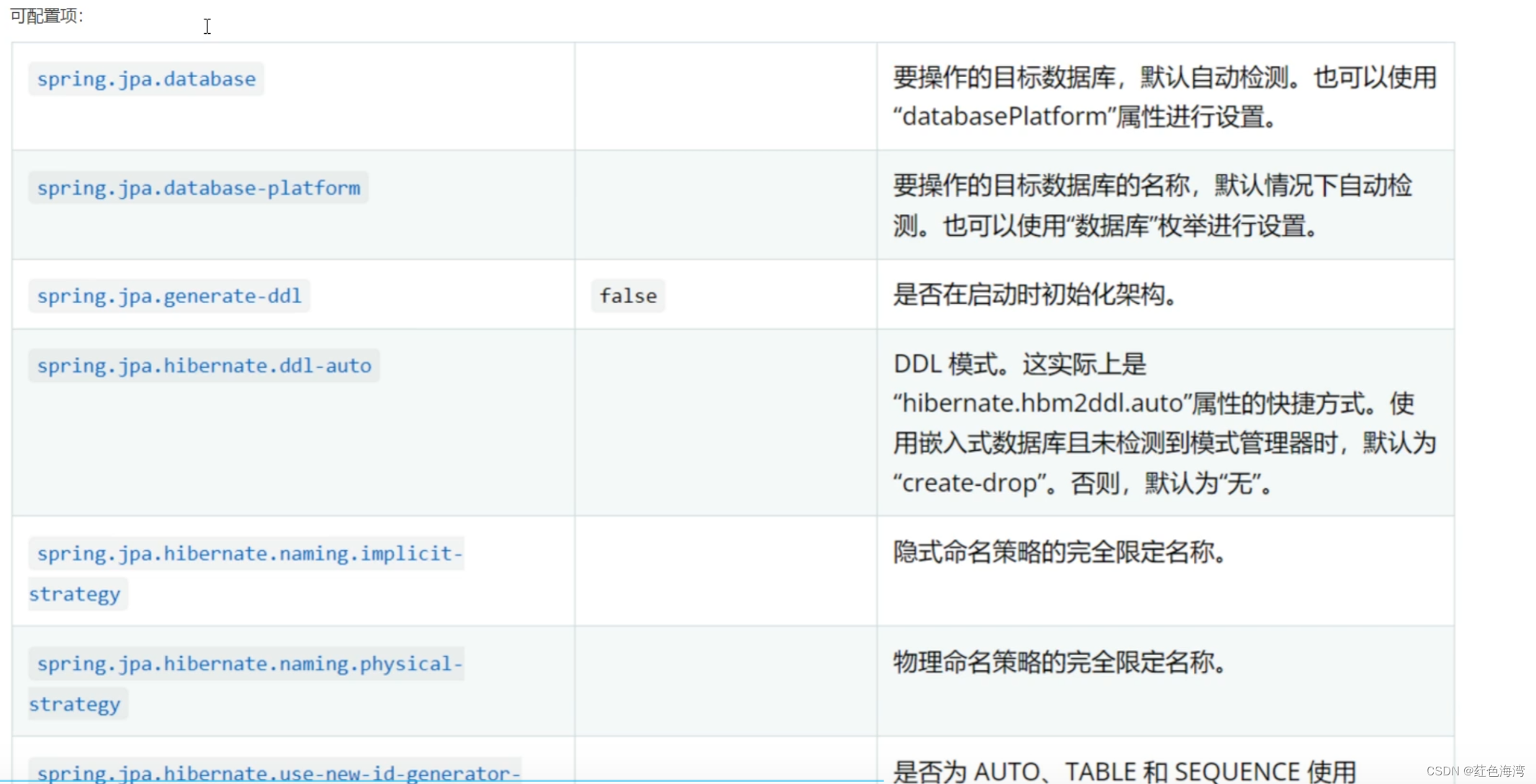
SpringData JPA 整合Springboot
1.导入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...

打工人副业变现秘籍,某多/某手变现底层引擎-Stable Diffusion 黑白老照片上色修复
在这个时代,我们习惯于拥有高清、色彩丰富的照片,然而,那些古老的黑白色老照片由于年代的久远,往往会出现模糊、破损等现象。 那么今天要给大家介绍的是,用 Stable Diffusion 来修复老照片。 前段时间 ControlNet 的除了上线了“IP-Adapter”模型以外还增加另一个…...

第十三章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2…...

大模型应用_PrivateGPT
https://github.com/imartinez/privateGPT 1 功能 整体功能,想解决什么问题 搭建完整的 RAG 系统,与 FastGPT相比,界面比较简单。但是底层支持比较丰富,可用于知识库的完全本地部署,包含大模型和向量库。适用于保密级…...
[Android] ubuntu虚拟机上搭建 Waydroid 环境
1.安装虚拟机 略 2.安装waydroid Ubuntu/Debian and derivatives For Droidian and Ubuntu Touch, skip directly to the last step Install pre-requisites sudo apt install curl ca-certificates -y Add the official repository curl https://repo.waydro.id | sudo…...

LeedCode刷题---滑动窗口问题(二)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、将X减到0的最小操作数 题目链接:将 x 减到 0 的最小操作数 题目描述 给你一个整数数组 nums 和一个整数 x 。每一…...
pycharm依赖管理(不要用pip freeze)
在使用python虚拟环境时,可以使用requirements.txt来管理当前项目的依赖。 注意,不要用 pip freeze > requirements.txt 这个命令,因为它会引入很多无关的包。 可以使用 pipreqs ./ --encodingutf-8 ./ 表示当前项目的目录࿰…...

[Kafka 常见面试题]如何保证消息的不重复不丢失
文章目录 Kafka1. Kafka如何保证不丢失消息?生产者数据的不丢失消费者数据的不丢失Kafka集群中的broker的数据不丢失 2. Kafka中的消息是否会丢失和重复消费?1. 消息发送2. 消息消费 3. Kafka 的设计是什么样的呢?4. 数据传输的事务定义有哪三…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
