电子技术——CMOS 逻辑门电路
电子技术——CMOS 逻辑门电路
在本节我们介绍如何使用CMOS电路实现组合逻辑函数。在组合电路中,电路是瞬时发生的,也就是电路的输出之和当前的输入有关,并且电路是无记忆的也没有反馈。组合电路被大量的使用在当今的数字逻辑系统中。
晶体管的开关模型
CMOS数字电路使用NMOS和PMOS晶体管作为开关使用。之前,我们知道,MOS可以工作在三极管区(相当于开关闭合),也可工作在截止区(相当于开关断开)。
特别的,当一个NMOS作为闭合的开关的时候,此时栅极电压处于高电压,相当于一个从漏极到源极直接相当小的一个电阻 RonR_{on}Ron 或 rDSr_{DS}rDS ,通常处在高电压 VDDV_{DD}VDD 状态,表示逻辑1。相反,当栅极为低电压的时候,此时MOS截止,表示逻辑0,没有电流流过MOS,如图:
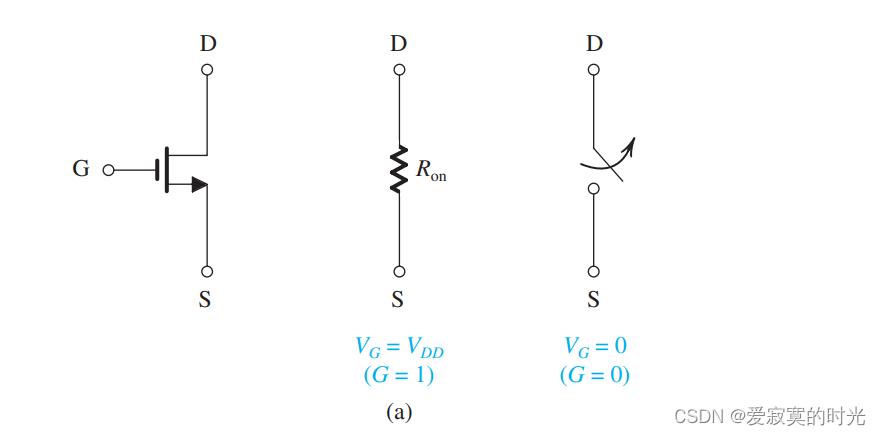
而PMOS则工作在相反的状态,栅极高电压,MOS管截止,栅极低电压,MOS管导通,如图:
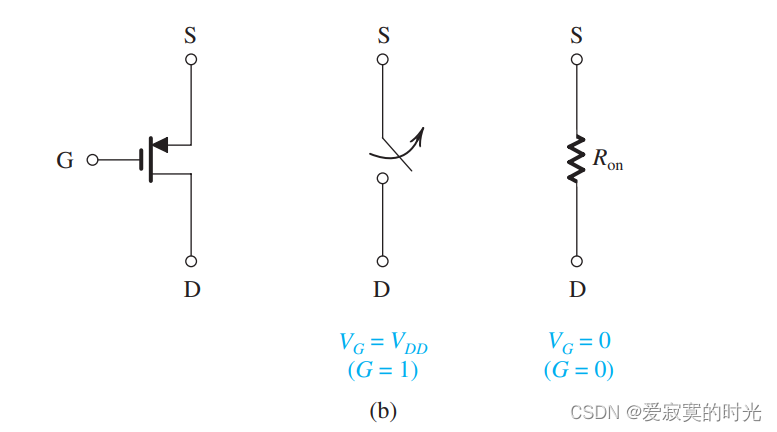
我们观察到MOS管的栅极通常是逻辑控制输入节点,通常作为逻辑门的输入端。
CMOS反相器
在了解MOS开关的工作方式之后,先让我们制作一个反相器。正如其名,反相器可以逆转输入的逻辑,即输入0输出1,反之亦然。因此该功能可以使用布尔函数表示为:
Y=X‾Y = \overline{X} Y=X
其抽象电路模型和实现电路如图所示:
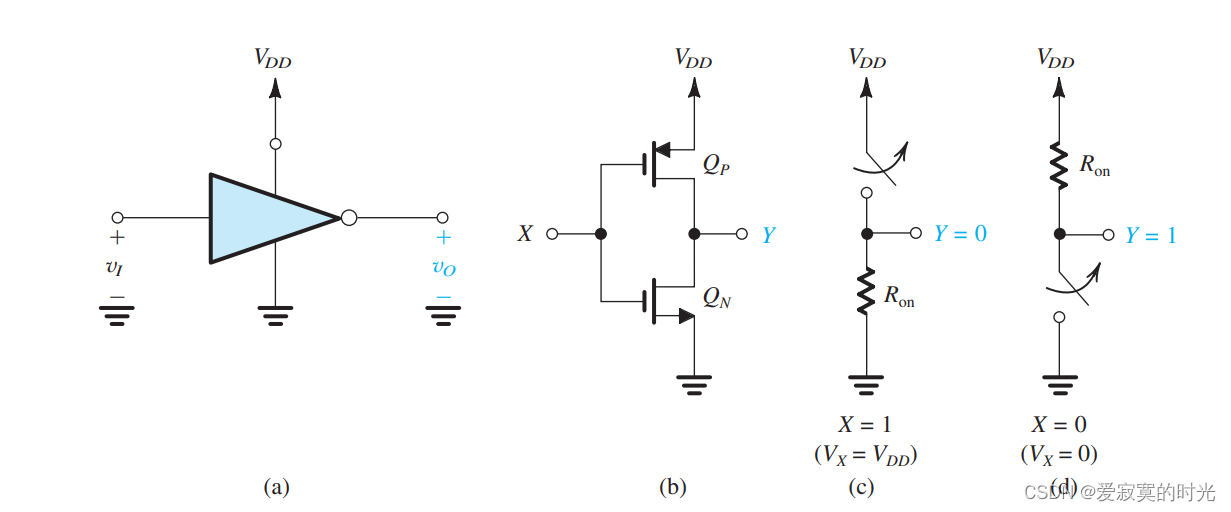
它由一对CMOS组成,栅极相连,作为输入端 XXX ,漏极相连作为输出端 YYY 。当 X=1X=1X=1 的时候,即 VX=VDDV_X = V_{DD}VX=VDD ,此时PMOS截止,而NMOS导通,输出 Y=0Y = 0Y=0 。当 X=0X=0X=0 的时候,PMOS导通而NMOS截止,此时输出 Y=1Y=1Y=1 。
CMOS逻辑门的一般结构
由上面的反相器我们能总结出CMOS逻辑门的一般结构,反相器由一个NMOS 下拉晶体管 和一个PMOS 上拉晶体管 组成。CMOS逻辑门由两个网络组成:一是 下拉网络PDN 由NMOS组成 ,二是 上拉网络PUN 由PMOS组成。如图:
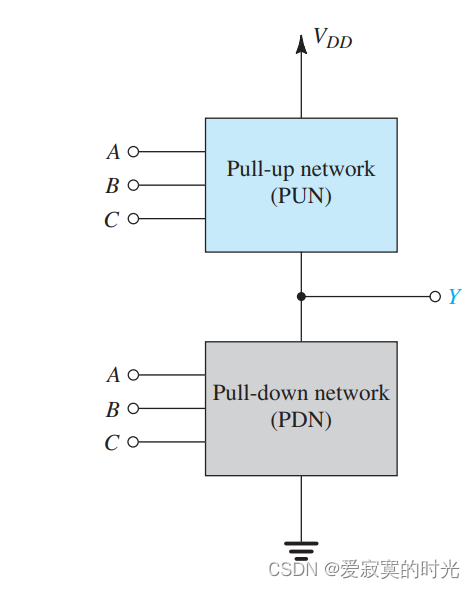
这两个网络都受到输入变量的控制,做出相反的行为,上图是一个三变量输入的逻辑门,当输入变量满足PDN条件的时候,此时PDN网络导通,而PUN网络截止,输出 Y=0Y=0Y=0 ,反之亦然。
因此,我们可以根据不同的PDN和PUN的实现,来实现与门、或门等一些基本的门电路,下图是一些PDN网络的例子:
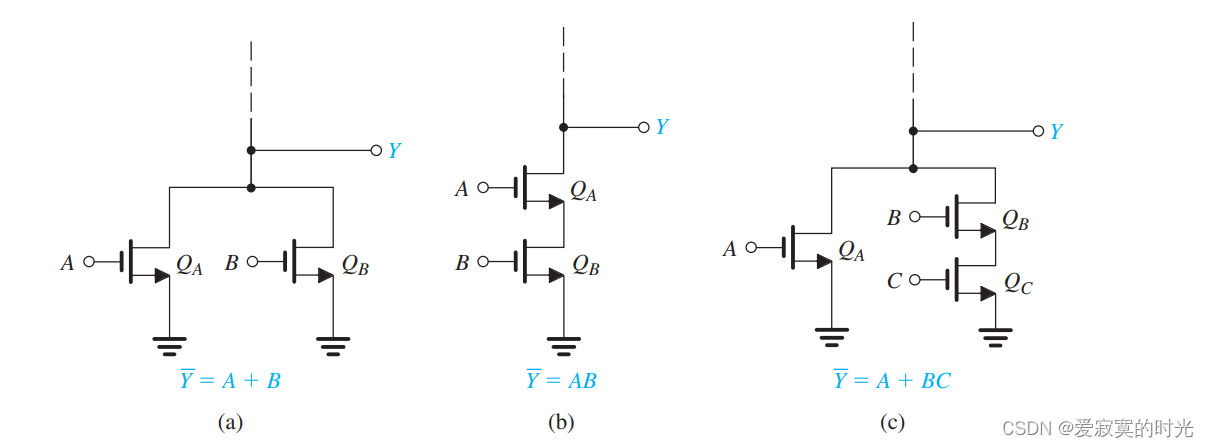
在图(a)我们发现当 A=1A=1A=1 的时候, QAQ_AQA 导通此时 Y=0Y = 0Y=0 ,同样的对于 B=1B = 1B=1 ,QBQ_BQB 导通此时 Y=0Y = 0Y=0 ,因此图(a)是一个或门的PDN实现,可以表示为:
Y‾=A+B\overline{Y} = A + B Y=A+B
或是:
Y=A+B‾Y = \overline{A + B} Y=A+B
图(b)必须两个NMOS全部导通才能输出,是一个与门结构,可以表示为:
Y‾=AB\overline{Y} = AB Y=AB
或是:
Y=AB‾Y = \overline{AB} Y=AB
最后一个例子图©是一个组合逻辑,可以表示为:
Y‾=A+BC\overline{Y} = A + BC Y=A+BC
或者等效于:
Y=A+BC‾Y = \overline{A + BC} Y=A+BC
接下来我们考虑一些PUN的一些例子,如图:

图(a)当 A=0A = 0A=0 或是 B=0B = 0B=0 的时候输出 Y=1Y = 1Y=1 表示为:
Y=A‾+B‾Y = \overline{A} + \overline{B} Y=A+B
图(b)当 A=0A=0A=0 并且 B=0B= 0B=0 的时候导通,表示为:
Y=A‾B‾Y = \overline{A} \ \overline{B} Y=A B
而图©表示为:
Y=A‾+B‾C‾Y = \overline{A} + \overline{B} \ \overline{C} Y=A+B C
在学习完PDN和PUN理论之后,我们就可以准备搭建我们的门电路了。首先,为了方便,我们不再使用模拟电路中的MOS符号,而是使用一种更加方便的数字电路MOS表示符号,如图:
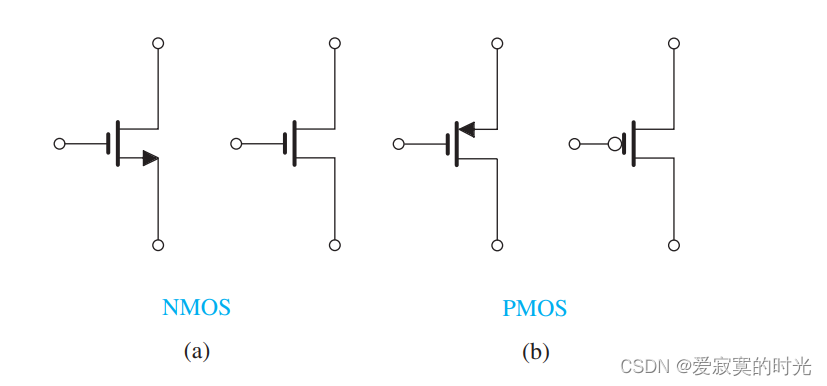
上图中左边的符号是模拟MOS表示,而右边是数字MOS表示,对于PMOS我们发现在栅极的地方有一个小圈,这表示当输入是低电压的时候才导通。除此之外,数字MOS忽略了漏极栅极之分。
或非门NOR电路
首先我们考虑一个CMOS的或非门电路:
Y=A+B‾=A‾B‾Y = \overline{A + B} = \overline{A} \ \overline{B} Y=A+B=A B
等式中间给出了PDN实现,等式右边给出了PUN实现,将两个实现组合在一起,我们得到:
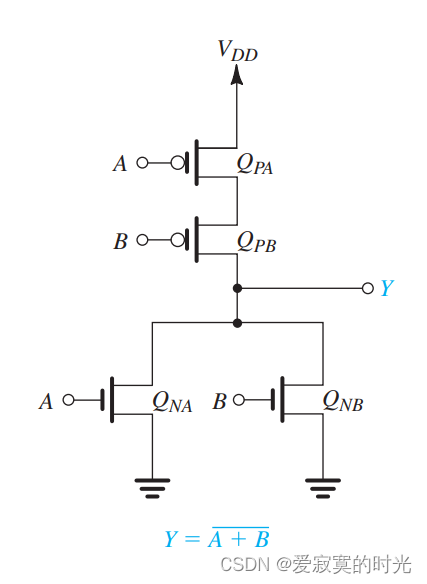
与非门NAND电路
与非门电路可以表示为:
Y=AB‾=A‾+B‾Y = \overline{AB} = \overline{A} + \overline{B} Y=AB=A+B
等式中间给出了PDN实现,等式右边给出了PUN实现,将两个实现组合在一起,我们得到:
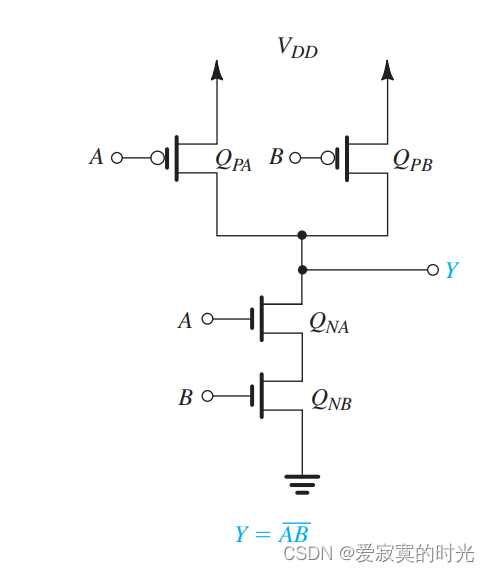
一个更复杂的门电路
考虑下面的组合布尔表达式:
Y=A(B+CD)‾Y = \overline{A(B+CD)} Y=A(B+CD)
因为PDN是整体反相,因此可以直接给出PDN实现,对于PUN则是变量反相,可以通过德·摩根定律展开表达式:
Y=A‾+B‾(C‾+D‾)Y = \overline{A} + \overline{B}(\overline{C} + \overline{D}) Y=A+B(C+D)
给出实现:

需要注意的是,有时候并不总是可以通过对偶律来获得两个网络的实现。对于以上情况,需要更加复杂的布尔逻辑推导。
异或门XOR电路
另一个重要的逻辑电路是异或门电路,表示为:
Y=AB‾+A‾BY = A \overline{B} + \overline{A}B Y=AB+AB
我们观察到给出 YYY 我们可以先考虑PUN,但不幸的是,表达式不是由每个变量的反相值构成,因此我们需要额外的反相器,如图的PUN:
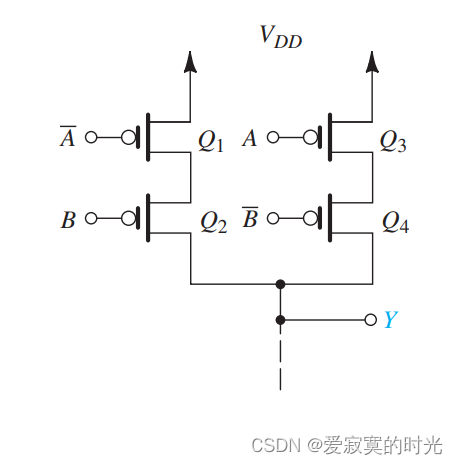
如上图,左边的 A‾\overline{A}A 和右边的 B‾\overline{B}B 都需要先反相才能输入到PUN中,因此需要额外的两个反相器,对于PDN,通过对偶变换可以得到:
Y‾=AB+A‾B‾\overline{Y} = AB + \overline{A} \ \overline{B} Y=AB+A B
对应的PDN实现为:
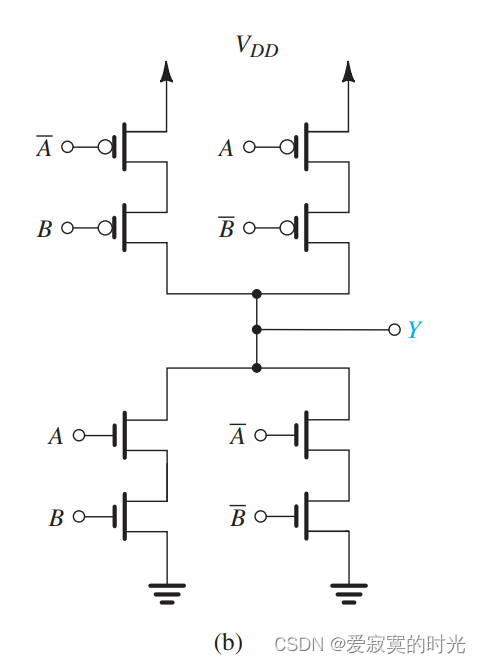
同样需要两个额外的反相器。则此异或门电路总共需要12个晶体管。
有趣的是,上图中两个PDN和PUN网络不是对偶网络,实际上,PDN和PUN网络对偶并不是必要条件。
总结
- PDN网络可以通过关于非互补变量的 Y‾\overline{Y}Y 的表达式得到,若表达式中存在互补变量,需要额外的输入反相器。
- PUN网络可以通过关于互补变量的 YYY 的表达式得到,若表达式中存在非互补变量,需要额外的输入反相器。
- PDN网络可以将PUD网络进行对偶得到,反之亦然。
相关文章:

电子技术——CMOS 逻辑门电路
电子技术——CMOS 逻辑门电路 在本节我们介绍如何使用CMOS电路实现组合逻辑函数。在组合电路中,电路是瞬时发生的,也就是电路的输出之和当前的输入有关,并且电路是无记忆的也没有反馈。组合电路被大量的使用在当今的数字逻辑系统中。 晶体管…...

【C++】C++11 新特性
目录 1.列表初始化 1.1. C98中使用{}初始化的问题 1.2. 内置类型的列表初始化 1.3. 自定义类型的列表初始化 2. 变量类型推导 2.1. 为什么需要类型推导 2.2. decltype类型推导 2.2.1 为什么需要decltype 2.2.2. decltype 3. 对默认成员的控制(default、delete) 3.1. …...

JPA 相关注解说明
jpa相关注解 JPA(Java Persistence API)是一种Java规范,定义了一套标准的对象关系映射(ORM)API,用于将Java对象映射到关系型数据库中。JPA旨在统一各种ORM框架之间的差异,提供一种标准化的ORM解…...

SAP 生产订单/流程订单中日期的解释
SAP 生产订单/流程订单中日期的解释 基本开始日期:表示订单的开始日期 基本完成日期:表示订单的完成日期 我们在输入基本开始日期和基本完成日期时需要关注 调度 下面的“类型”,其中有向前、向后、当天日期等: 调度类型 为向前…...
Java设计模式笔记——七大设计原则
系列文章目录 第一章 Java 设计模式之七大设计原则 文章目录系列文章目录前言一、单一职责原则1.案例分析2.改进二、开闭原则1.案例分析2.改进三、里氏替换原则1.案例分析2.改进四、依赖倒转原则五、接口隔离原则1.案例分析2.改进六、合成复用原则1.案例分析2.改进七、迪米特原…...
记录第一次接口上线过程
新入职一家公司后,前三天一直在学习公司内部各种制度文化以及考试。 一直到第三天组长突然叫我过去,给了一个需求的思维导图,按照这个需求写这样一个接口, 其实还不错,不用自己去分析需求,按照这上面直接开…...

时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含验证Loss曲线)
时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含训练和验证Loss曲线) 目录 时序预测 | MATLAB实现Rmsprop算法优化LSTM长短期记忆神经网络时间序列多步预测(滚动预测未来,多指标,含训练和验证Loss曲线)效果一览基本描…...

如何利用Level2行情数据接口追板和交易股票?
十档行情看得更深的A股行情软件,我们在盘口数据中可以看到,买一到买五以及卖一到卖五,共10个价位的挂单情况,但基于上证所的level-2行情软件,视野则扩展到了买一到买十以及卖一到卖十数据,无疑比所有免费软…...

MySQL常用的聚合函数
聚合函数聚合函数对一组值进行运算,并返回单个值。也叫组合函数函数作用COUNT(*|列名) 统计查询结果的⾏数AVG(数值类型列名)求平均值,返回指定列数据的平均值SUM (数值类型列名)求和,返回指定列的总和MAX(列名)查询指定列的最⼤值MIN(列名)查…...
如何评估模糊测试工具-unibench的使用
unibench是一个用来评估模糊测试工具的benchmark。这个benchmark集成了20多个常用的测试程序,以及许多模糊测试工具。 这篇文章(https://zhuanlan.zhihu.com/p/421124258)对unibench进行了简单的介绍,本文就不再赘诉,…...

2023初级会计详细学习计划打卡表!自律逆袭,一次上岸!
2023年初级会计职称考试报名时间:2月7日-28日考试时间:5月13日—17日给大家整理了《经济法基础》和《初级会计实务》两科超实用的学习打卡表重要程度、难易度、易错点、要求掌握内容、章节估分等都全部总结在一起,一目了然!为什么…...

【Python】Python项目打包发布(四)(基于Nuitka打包PySide6项目)
Python项目打包发布汇总 【Python】Python项目打包发布(一)(基于Pyinstaller打包多目录项目) 【Python】Python项目打包发布(二)(基于Pyinstaller打包PyWebIO项目) 【Python】Pytho…...
)
一起Talk Android吧(第五百一十三回:Java中的byte数组与int变量相互转换)
文章目录整体思路示例代码各位看官们大家好,上一回中咱们说的例子是"自定义Dialog",这一回中咱们说的例子是" Java中的byte数组与int变量相互转换"。闲话休提,言归正转, 让我们一起Talk Android吧!在实际项目…...
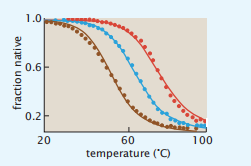
22《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》中文分享
《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》 本人能力有限,如果错误欢迎批评指正。 第五章:Folding and Aggregation Are Cooperative Transitions (折叠和聚合是同时进行的) -蛋白质折叠的协同作…...
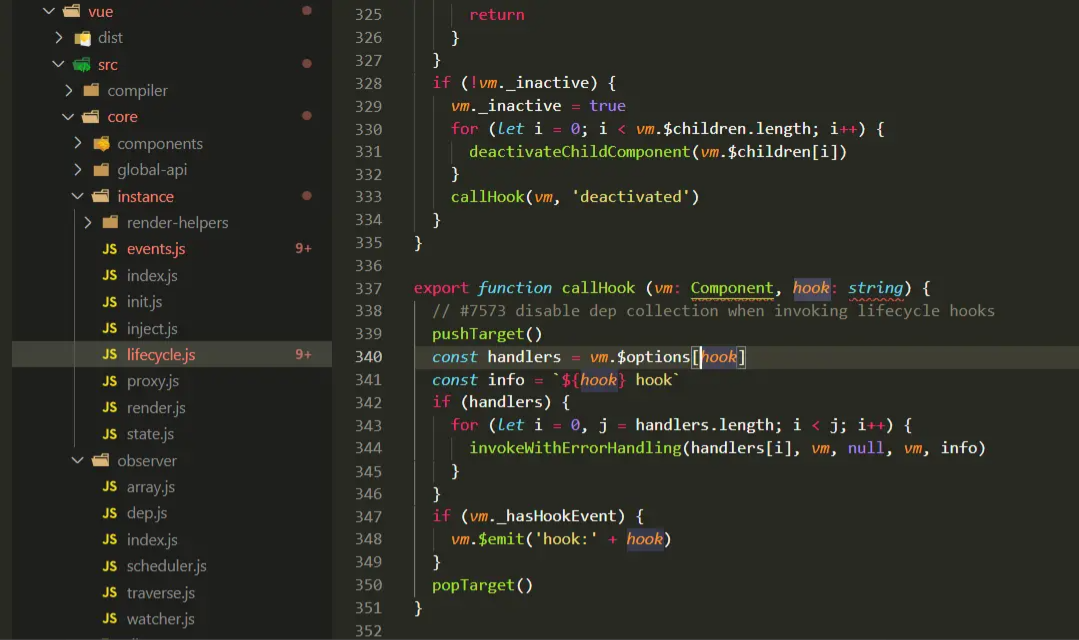
vue2 @hook 的解析与妙用
目录前言几种用法用法一 将放在多个生命周期的逻辑,统一到一个生命周期中用法二 监听子组件生命周期运行的情况运用场景场景一 许多时候,我们不得不在不同的生命周期中执行某些逻辑,并且这些逻辑会用到一些通用的变量,这些通用变量…...
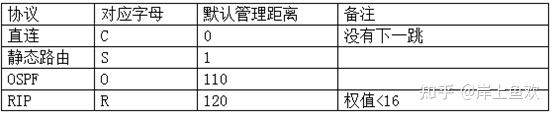
网络技术|网络地址转换与IPv6|路由设计基础|4
对应讲义——p6 p7NAT例题例1解1例2解2例3解3例4解4一、IPv6地址用二进制格式表示128位的一个IPv6地址,按每16位为一个位段,划分为8个位段。若某个IPv6地址中出现多个连续的二进制0,可以通过压缩某个位段中的前导0来简化IPv6地址的表示。例如…...

MySQL运维知识
1 日志1.1 错误日志1.2 二进制日志查看二进制日志:mysqlbinlog ./binlog.000007purge master logs to binlog.000006reset mastershow variables like %binlog_expire_logs_seconds%默认二进制文件只存放30天,30天后会自动删除。1.3 查询日志1.4 慢查询日…...

易基因-MeRIP-seq揭示衰老和神经变性过程中m6A RNA甲基化修饰的保守下调机制
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。2023年02月22日,《美国国家科学院院刊》(Proc Natl Acad Sci USA)期刊发表了题为“Conserved reduction of m6A RNA modifications during aging and neurodegeneration is lin…...
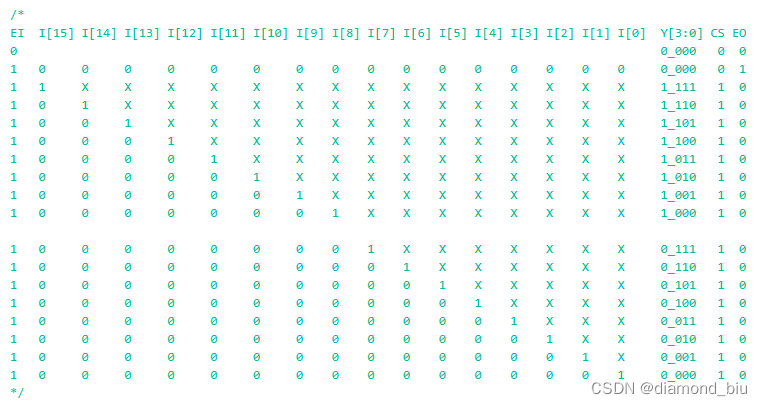
暑期实习准备——Verilog手撕代码(持续更新中。。。
暑期实习准备——手撕代码牛客刷题笔记Verilog快速入门VL4 移位运算与乘法VL5 位拆分与运算VL6 多功能数据处理器VL8 使用generate…for语句简化代码VL9 使用子模块实现三输入数的大小比较VL11 4位数值比较器电路VL12 4bit超前进位加法器电路VL13 优先编码器电路①VL14 用优先编…...
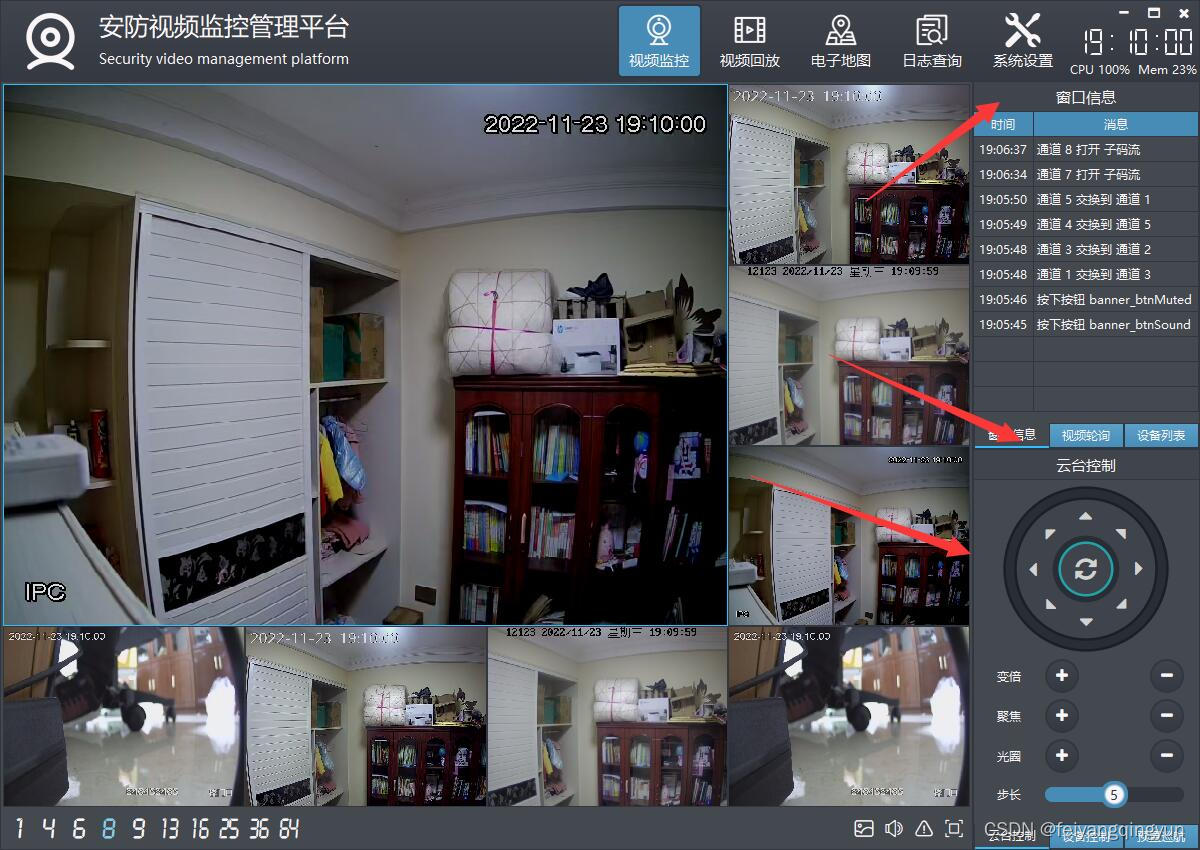
Qt音视频开发19-vlc内核各种事件通知
一、前言 对于使用第三方的sdk库做开发,除了基本的操作函数接口外,还希望通过事件机制拿到消息通知,比如当前播放进度、音量值变化、静音变化、文件长度、播放结束等,有了这些才是完整的播放功能,在vlc中要拿到各种事…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
