跳跃游戏 + 45. 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
解析:
每次遍历,只需要贪心跳到最远即可。
class Solution {
public:bool canJump(vector<int>& nums) {int len = nums[0];for(int i = 1;i < nums.size();i++){if(len >= i){len = max(len,nums[i]+i);}}return len >= nums.size()-1;}
};时间复杂度为O(n)
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是2。从下标为 0 跳到下标为 1 的位置,跳1步,然后跳3步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4] 输出: 2
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
解析:
这个是跳到最后一个位置的最小次数。
反向思想,从后向前,当前位置可以是哪个最先的下标跳跃而来的。
class Solution {
public:int jump(vector<int>& nums) {int p = nums.size()-1;int ans = 0;while(p > 0){for(int i = 0;i < p;i++){if(i+nums[i] >= p){p = i;ans++;break;}}}return ans;}
};时间复杂度为O(n*n);
在进行优化,我们可以这么想。我们每次跳到最远的。在从当前位置遍历到的第一次跳到最远的。
在这个最远的区间内,我们又可以更行更远的。以此类推,贪心正向遍历,时间复杂度为O(n)
class Solution {
public:int jump(vector<int>& nums) {int m = 0,r = 0;int ans = 0;for(int i = 0;i < nums.size()-1;i++) //最后一步不用跳{m = max(m,i+nums[i]);if(i == r) // r为区间的左端点{r = m;ans++;}}return ans;}
};2580. 统计将重叠区间合并成组的方案数
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
- 每个区间只属于一个组。
- 两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间
[1, 3]和[2, 5]有交集,因为2和3在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]] 输出:2 解释: 两个区间有交集,所以它们必须在同一个组内。 所以有两种方案: - 将两个区间都放在第 1 个组中。 - 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]] 输出:4 解释: 区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。 同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。 所以总共有 4 种分组方案: - 所有区间都在第 1 组。 - 所有区间都在第 2 组。 - 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。 - 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
1 <= ranges.length <= 105ranges[i].length == 20 <= starti <= endi <= 109
解析:
区间要不重和,所以不重和的区间有两种选择,去第一个还是去第二个。我们对左端点进行排排序。当前区间右端点判断是否和下一个区间的左端的有重合。如果没有,则可以看错新的全,他可以去第一个也可以去第二个。
class Solution {
public:
const int MOD = 1e9 + 7;int countWays(vector<vector<int>>& ranges) {sort(ranges.begin(),ranges.end(),[](auto &a,auto &b){return a[0] < b[0];});int ans = 2,max_r = ranges[0][1];for(auto &p : ranges){if(p[0] > max_r){ans = ans*2%MOD;}max_r = max(max_r,p[1]);}return ans;}
};时间复杂度为O(n*logn)
相关文章:

跳跃游戏 + 45. 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输…...
)
在Django中使用多语言(i18n)
在Django中使用多语言 配置中间件 MIDDLEWARE [......django.contrib.sessions.middleware.SessionMiddleware,django.middleware.locale.LocaleMiddleware, # 此行重点django.middleware.common.CommonMiddleware,...... ]配置翻译文件目录 根目录下创建目录locale # 国…...
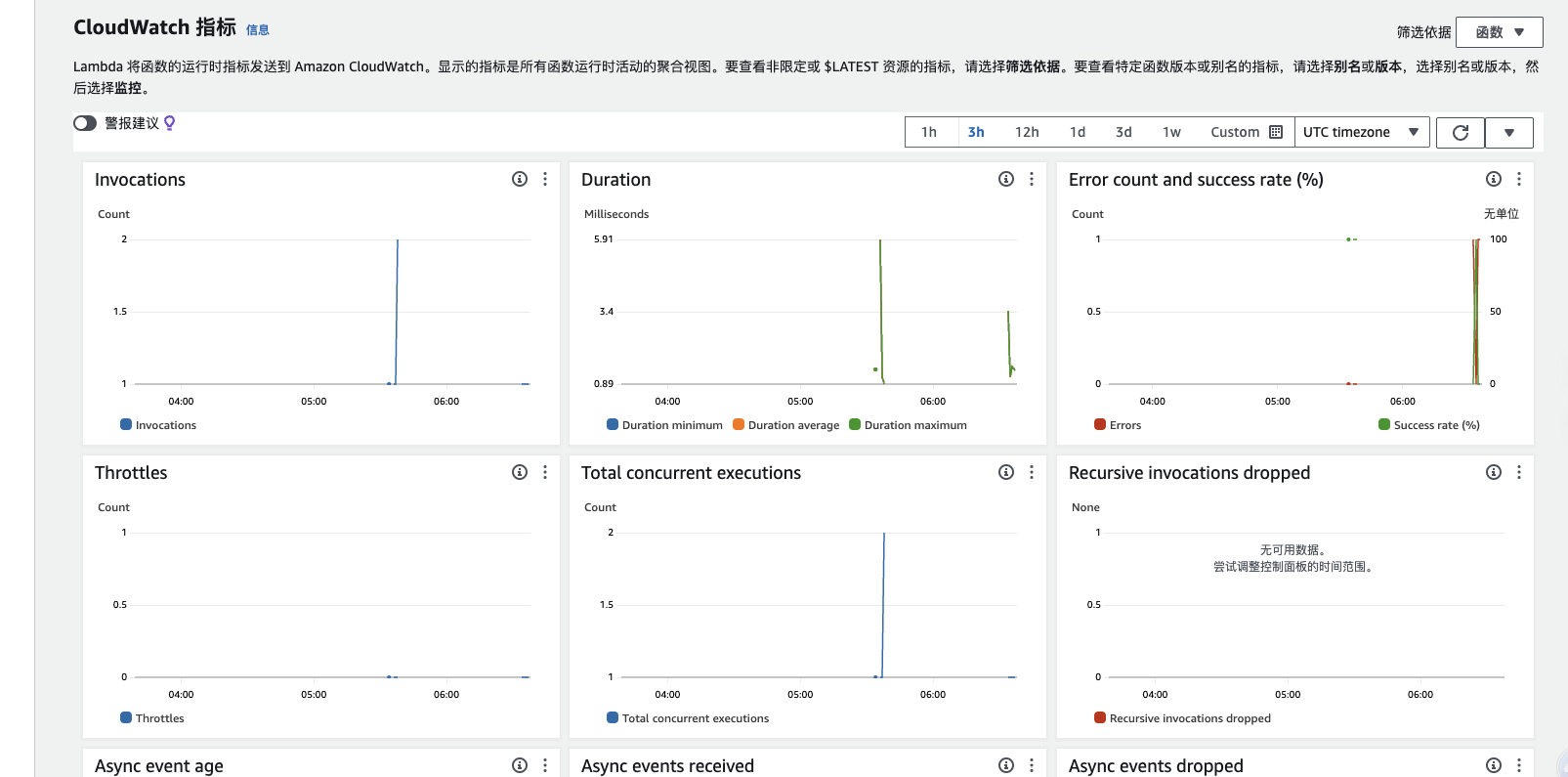
高性价比AWS Lambda无服务体验
前言 之前听到一个讲座说到AWS Lambda服务,基于Serverless无服务模型,另外官网还免费提供 100 万个请求 按月,包含在 AWS 免费套餐中是真的很香,对于一些小型的起步的网站或者用户量不大的网站,简直就是免费ÿ…...
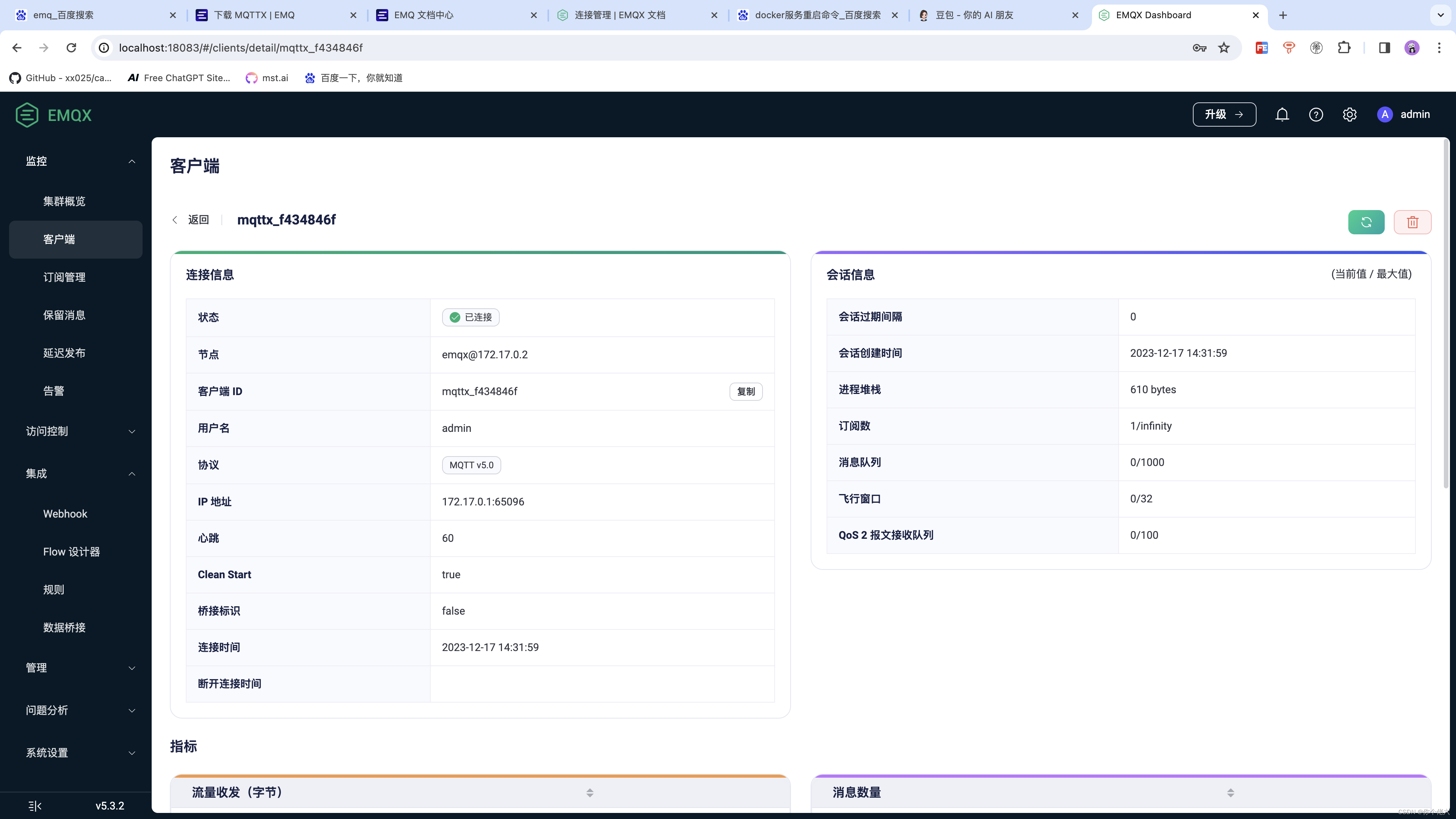
【物联网】EMQX(二)——docker快速搭建EMQX 和 MQTTX客户端使用
一、前言 在上一篇文章中,小编向大家介绍了物联网必然会用到的消息服务器EMQ,相信大家也对EMQ有了一定的了解,那么接下来,小编从这篇文章正式开始展开对EMQ的学习教程,本章节来记录一下如何对EMQ进行安装。 二、使用…...
2023 亚马逊云科技 re:lnvent 大会探秘: Amazon Connect 全渠道云联络中心
2023 亚马逊云科技 re:lnvent 大会探秘: Amazon Connect 全渠道云联络中心 前言一. Amazon Connect 介绍 🗺️二. Amazon Connect 使用教程 🗺️1.我们打开URl链接找到对应服务2.输入Amazon Connect选中第一个点击进入即可;3.在进入之后我们就…...

鸿蒙开发之用户隐私权限申请
一、简介 鸿蒙开发过程中可用于请求的权限一共有两种:normal和system_basic。以下内容摘自官网: normal权限 normal 权限允许应用访问超出默认规则外的普通系统资源。这些系统资源的开放(包括数据和功能)对用户隐私以及其他应用带…...

Docker笔记:简单部署 nodejs 项目和 golang 项目
docker 简单的维护 nodejs 项目容器 1 )Nodejs 程序 const express require(express) const app express()app.get(/, (req, res) > {res.send(首页) })app.get(/news, (req, res) > {res.send(news) })// dokcer 做端口映射不要指定ip app.listen(3000)2…...

java内置的数据结构
Java语言提供了许多内置的数据结构,包括: 1. 数组(Array):数组是最基本的数据结构之一,它是一个有序的元素集合,每个元素都有一个对应的索引。在Java中,数组可以通过声明和初始化来创…...
轻松搭建FPGA开发环境:第三课——Vivado 库编译与设置说明
工欲善其事必先利其器,很多人想从事FPGA的开发,但是不知道如何下手。既要装这个软件,又要装那个软件,还要编译仿真库,网上的教程一大堆,不知道到底应该听谁的。所以很多人还没开始就被繁琐的开发环境搭建吓…...
PostgreSQL-Dropdb命令删除数据库)
【PostgreSQL】从零开始:(十一)PostgreSQL-Dropdb命令删除数据库
dropdb命令删除数据库 命令 [postgrespostgre-sql bin]$ dropdb --help dropdb removes a PostgreSQL database.Usage:dropdb [OPTION]... DBNAMEOptions:-e, --echo show the commands being sent to the server-f, --force try to terminate …...

UDP网络编程其他相关事项
netstat指令 netstat -an 可以查看当前主机网络情况,包括端口监听情况和网络连接情况。 netstat -an | more 可以分页显示。 要求在dos控制台下执行。 说明:(1)Listening表示某个端口在监听;(2…...

Redhat LINUX 9.3 + PG 16.1 搭建主备流复制
一直想搭建一个PG流复制,最近正好有一个新环境,操作系统是最新的,rhel 9.3,数据库是最新的 pg 16.1,借鉴了网上的步骤,尤其是小工到专家的内容,在此谢过。 1.安装环境 1)IP: 主:192.168.133.151…...

kafka设置消费者组
安装部署后 consumer.properties group.idtest-group 单机测试,自己开俩窗口,一个测试消费者,一个测试生产者(创建消息那步) 创建主题 bin/kafka-topics.sh --create --bootstrap-server localhost:9092 --replica…...

Worker-Thread设计模式
Worker-Thread模式类似于工厂流水线,有时也称为流水线设计模式。线程池在某种意义上也算是Worker-Thread模式的一种实现,线程池初始化时创建线程类似于在流水线等待工作的工人,提交给线程池的Runnable接口类似于需要加工的产品,Ru…...
)
npm 安装包遇到问题的常用脚本(RequestError: socket hang up)
前言 最近在给一个基于 Electron 的开源项目做贡献,需要去安装一些 npm 库,由于众所周知的原因,经常会出现报错: npm ERR! path D:\Projects\project\node_modules\electron npm ERR! command failed npm ERR! command C:\Windo…...

活动 | Mint Blockchain 将于 2024 年 1 月 10 号启动 MintPass 限时铸造活动
MintPass 是由 Mint Blockchain 官方发行的 Mint 网络和社区的 NFT 通行证,将在 2024 年 1 月份启动限时铸造活动。今天这篇文章会着重向大家介绍即将举办的 MintPass 活动的基础信息。 MintPass 有 2 种类型: 类型 1:Mint Genesis NFT Mint…...

Android动画(四)——属性动画ValueAnimator的妙用
目录 介绍 效果图 代码实现 xml文件 介绍 ValueAnimator是ObjectAnimator的父类,它继承自Animator。ValueAnimaotor同样提供了ofInt、ofFloat、ofObject等静态方法,传入的参数是动画过程的开始值、中间值、结束值来构造动画对象。可以将ValueAnimator看…...

C语言飞机大战
一、前言 [设计难度 : ★☆☆☆☆ [参考书籍:《C语言课程设计与游戏开发实践教程》 [主要涉及知识:函数封装 循环判断语句 [程序运行效果图: [主要的游戏功能: 通过按键’w’,‘s’,‘a’,d’分别实现飞机的上下左右移动 按空格…...

js 原型 和 原型链
function Person(name,age){ this.name name this.age age } var p new Person(张三,11) //创建构造函数的时候,解析器会自动为构造函数创建prototype属性,prototype属性对应的对象就是原型对象 // prototype 翻译为 原…...

如何利用SD-WAN节省运维成本和简化运维工作?
在当今数字化时代,企业对于网络的要求越来越高,需要保障网络的安全性、可靠性和灵活性。同时,随着企业的上云和远程办公等需求的增加,传统的WAN网络已经无法满足企业的需求。因此,SD-WAN技术应运而生。 SD-WAN节省运维…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
